Synchronization of Uncertain Chaotic Systems using Generalized
Predictive Control based on Fuzzy PID Controllers
Zakaria Driss and Noura Mansouri
Laboratory of Automatics and Robotic
Department of Electronics, Faculty of Engineer Sciences, University of Constantine 1, 25000, Constantine, Algeria
Keywords:
GPC, Fuzzy PID Controllers, Chaotic Systems, Synchronization.
Abstract:
In this paper, we investigate the synchronization of chaotic systems with unknown parameters using gener-
alized predictive control based on fuzzy PID controllers. In order to verify the efficiency of the proposed
method, fuzzy PD+I and fuzzy PI+D controllers are successively used with and without prediction terms for
the synchronization of two uncertain Lorenz systems. For fuzzy PD+I controller, the prediction terms seem to
be efficient for the synchronization. However, with the fuzzy PI+D controller, they make a noise and worsen
the performance of the controller.
1 INTRODUCTION
Synchronization of chaotic systems has been widely
investigated in the last decades. Due to their sensi-
tivity to initial conditions and random behavior, they
have been categorized among one of the most inter-
esting topics of nonlinear science. Uncertainties on
parameters are another problem that worsens the task
of synchronization. Many classical approaches failed
to reach the synchronization and some advanced con-
trol approaches and improved schemes such as fuzzy
logic control(FLC) (Lam and Leung, 2006), neural
network(NN) (Lam and Seneviratne, 2007), adaptive
control strategy (Sun et al., 2013), are used to resolve
this problem.
Model predictive control (MPC) (Dumur and
Boucher, 1994) is a control approach which con-
sists in using a model of a system to predict its out-
put over an extended horizon. In the presence of
uncertainties, self-tuning and model-reference adap-
tive control(MRAC) were used with MPC to solve
many problems such as an open-loop unstable plant,
a nonminimum-phase plant, a plant with variable or
unknown dead-time and a plant with unknown or-
der. However, there was not a general algorithm to
solve all these problems at once until the establish-
ment of a general algorithm by D.W. Clarke (Clarke
et al., 1987) in 1985 called generalized predictive con-
trol(GPC).
The drawback of GPC is the number of mathemat-
ical steps the algorithm requests. In order to fix this
problem, several advanced control approaches have
been involved in GPC such as fuzzy-model-based ap-
proach (Lam and Leung, 2006), Neural-network (Jin-
quan and Lewis, 2003), and PSO-based model pre-
dictive control (Wang and Xiao, 2005). One of the
most interesting approaches (Lu et al., 2001) is by
involving fuzzy PID controllers to minimize the cost
function and to ensure the convergence.
In this paper, we consider the performance of GPC
based on fuzzy PID controllers (Lu et al., 2001)
for the synchronization of uncertain chaotic systems.
Fuzzy PI+D and fuzzy PD+I controllers are succes-
sively used to check the performance of the proposed
control method in the presence or absence of predic-
tion terms. For the prediction of the future variation
of the master and the salve system, an ARX model
is used. To verify the above proposed approach per-
formance, we apply it for the synchronization of two
uncertain Lorenz systems.
The rest of the paper is arranged as follows: Sec-
tion 2 presents synchronization of chaotic systems.
GPC based on fuzzy PID controllers is introduced
in Section 3. A brief description of fuzzy PI+D and
fuzzy PD+I controllers in Section 4. Simulation re-
sults are given in Section 5. Conclusions are given in
Section 6.
Driss, Z. and Mansouri, N..
Synchronization of Uncertain Chaotic Systems using Generalized Predictive Control based on Fuzzy PID Controllers.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 2: FCTA, pages 25-30
ISBN: 978-989-758-157-1
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
25

2 SYNCHRONIZATION OF
UNCERTAIN CHAOTIC
SYSTEMS
Let’s consider two n-dimensional chaotic systems,
one is designed as the master system:
˙x
m
= g
m
(x,t), 1 ≤ m ≤ n
(1)
x = [x
1
,x
2
,..., x
n
] ∈ ℜ
n
and the second is the controlled slave system:
˙y
m
= f
m
(y,t) +u
m
(t), 1 ≤ m ≤ n
(2)
y = [y
1
,y
2
,..., y
n
] ∈ ℜ
n
f and g represent unknown nonlinear functions,
and u ∈ ℜ
n
is the control input.
The Synchronization problem can be considered
as a control problem which consists in the design of
an appropriate control law u(t) such that:
lim
t→∞
k
y(t) − x(t)
k
→ 0
(3)
The error states between the two systems are given
by:
˙e
m
= f
m
(y,t) − g
m
(x,t) + u
m
(t), 1 ≤ m ≤ n
(4)
And the objective is how to design an efficient control
law u
m
(t) such that the error states converge to zero
when the time goes further.
3 GPC BASED ON FUZZY PID
CONTROLLERS
GPC algorithm consists mainly in minimizing a cost
function that contains the predicted values. There
have been many attempts to reduce the complexity
of the algorithm by involving some advanced con-
trol approaches. To avoid the tedious mathematical
steps, fuzzy PID controllers can be used (Lu et al.,
2001). For the synchronization, the following crite-
rion is used:
J
m
(k) =
∑
N
i=−1
[y
m
(k − i) − x
m
(k − i)]
2
+
λ
∑
N
c
j=0
[∆u
m
(k − j)]
2
J
m
(k) =
∑
N
i=−1
[e
m
(k − i)]
2
+ λ
∑
N
c
j=0
[∆u
m
(k − j)]
2
(5)
Where N is the prediction horizon, N
c
is the con-
trol increment horizon, ∆u
m
is the incremental output
of a controller, λ ≥ 0 is a control increment weight.
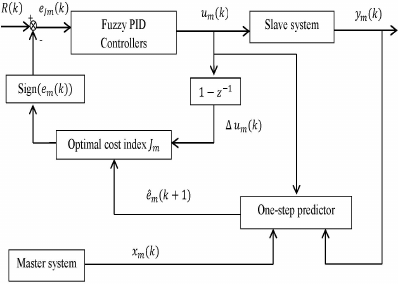
Figure 1 represents the main structure of GPC based
on fuzzy PID controllers for synchronization of un-
certain chaotic systems.
Figure 1: Block diagram of GPC based on fuzzy PID con-
trollers.
To get the predicted values of both systems, we
use ARX model. For the slave system, the model is
given by:
b
y
m
(k + 1) = a
1
y
m
(k) + a
2
y
m
(k − 1) + a
3
y
m
(k − 2)
+a
4
y
m
(k − 3) + b
1
u
m
(k − 1)
(6)
while the model of the master is given by:
b
x
m
(k + 1) = a
1
x
m
(k) + a
2
x
m
(k − 1) + a
3
x
m
(k − 2)
+a
4
x
m
(k − 3)
(7)
Where x
m
(k), y
m
(k) and u
m
(k) are the output of the
master system, the output of the slave system and the
control input respectively; a
1
,a
2
,a
3
,a
4
,b
1
are con-
stant parameters.
Thus, the one-step ahead predictor of the error states
is given as:
b
e
m
(k + 1) = a
1
e
m
(k) + a
2
e
m
(k − 1) + a
3
e
m
(k − 2)
+a
4
e
m
(k − 3) + b
1
u
m
(k − 1)
(8)
4 FUZZY PID CONTROLLERS
Fuzzy PI+D and fuzzy PD+I controllers are used to
perform two tasks: drive the salve system to track the
output of the master system , make the cost function
J
m
as small as possible.
The main steps to design both fuzzy PI+D and
fuzzy PD+I controllers are developed as follows. The
continuous form of a conventional fuzzy PI controller
(Tang et al., 2001) is given by:

u
PI
(t) = K
p
e
Jm
(t) + K
i
R
e
Jm
(t)dt
e
Jm
(t) = R(t) − J
m
(t) × Sign(e
m
(t))
(9)
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
26

Where R(t) is the reference for the optimal cost
index; K
p
is the constant proportional gain; K
i
is in-
tegral gain. e
Jm
(t) and e
m
(t) are the error signal from
the optimal index J
m
, the error between the master and
the slave system, respectively.
Using the Laplace transform, we obtain the analog
PI controller in the frequency domain
u
PI
(s) = (K
p
+
K
i
s
)E
Jm
(s)
(10)
By applying the bilinear transform s = (2/T )((z+
1)/(z − 1)), where T > 0 is the sampling period, we
obtain the discrete version
u
PI
(z) = (K
p
−
K
i
T
2
+
K
i
T
1−z
−1
)E
Jm
(z)
(11)
By taking
K
P
= K
p
−
K
i
T
2
, K
I
= K
i
T
and then using the inverse z-transform, we obtain
u
PI
(k) = u
PI
(k − 1) + T ∆u
PI
(k)
(12)
Where
∆u
PI
(k) = K
P
˙e
Jm
(k) + K
I
e
Jm
(k)
(13)
In equation (12), T ∆u
PI
(k) represents the incre-
mental output of a conventional PI controller.
By replacing the term T ∆u
PI
(k) with a fuzzy con-
trol action K
uPI
∆u
PI
(k) , we obtain the equation of the
fuzzy PI controller
u
PI
(k) = u
PI
(k − 1) + K
uPI
∆u
PI
(k)
(14)
where K
uPI
,K
P
andK
I
are constant control gains.
By applying the same steps, we obtain the fuzzy D
control law given by
u
D
(k) = −u
D
(k − 1) + K
uD
∆u
D
(k)
(15)
The overall fuzzy PI+D control law can be ob-
tained by algebraically summing the fuzzy PI control
law ( 14) and the fuzzy D law ( 15):
u
PID
(k) = u
PI
(k − 1) + K
uPI
∆u
PI
(k)
+u
D
(k − 1) − K
uD
∆u
D
(k)
(16)
Using the same steps of fuzzy PI+D (Lu et al.,
2001), we get the equations of fuzzy PD+I controller:
u
pdi
(k) = u
pd
(k) + u
i
(k)
(17)
Where
u
pd
(k) = −u
pd
(k − 1) + K
u
pd
∆u
pd
(k)
(a)
(b)
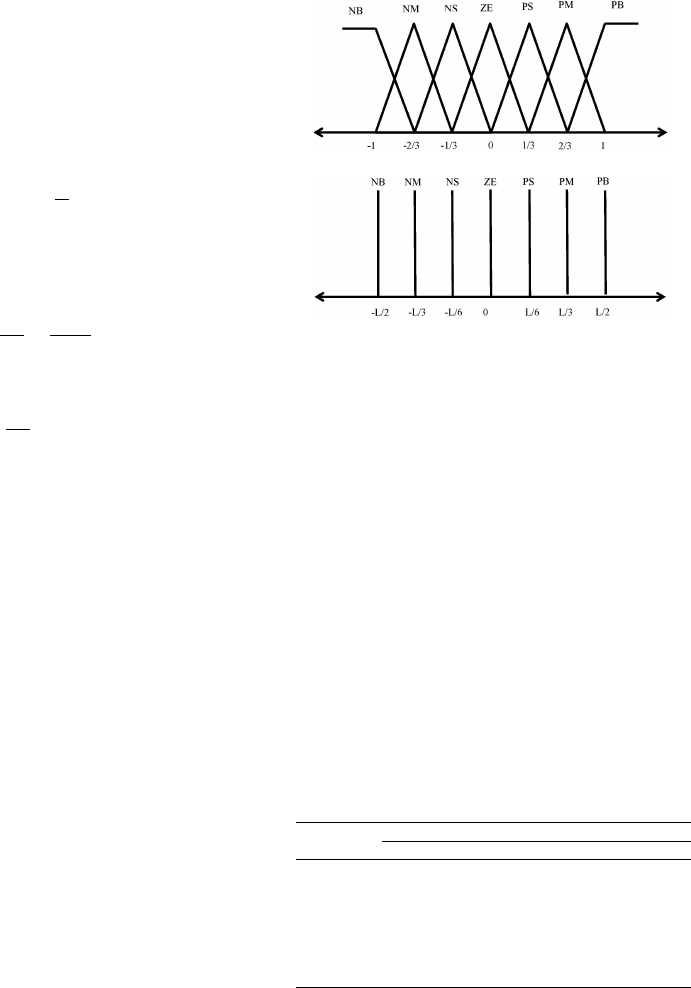
Figure 2: Input-output membership functions for fuzzy
PI+D and fuzzy PD+I controllers. (a) Membership func-
tions of e
Jm
, ˙e
Jm
. (b) Membership functions of ∆u
PI
(k),
∆u
D
(k), ∆u
pd
(k) and ∆u
i
(k).
u
i
(k) = u
i
(k − 1) + K
u
i
∆u
i
(k)
For the both controllers, seven triangular member-
ship functions are used for input linguistic variables
e
Jm
, ˙e
Jm
. The same number of functions is assigned to
output linguistic variables ∆u
PI
(k), ∆u
D
(k), ∆u
pd
(k)
and ∆u
i
(k).
The functions are designed as negative big (NB),
negative medium (NM), negative small (NS), zero
(ZE), positive small (PS), positive medium (PM) and
positive big (PB). The membership functions are
shown in Figure 2 while the fuzzy rule table is de-
signed in Table 1.
Table 1: Fuzzy rule of fuzzy PI+D and fuzzy PD+I con-
trollers.
˙e
Jm
PB PM PS ZE NS NM NB
e
Jm
PB NB NB NB NM NS NS ZE
PM NB NM NM NM NS ZE PS
PS NB NM NS NS ZE PS PM
ZE NB NM NS ZE PS PM PB
NS NM NS ZE PS PS PM PB
NM NS ZE PS PM PM PM PB
NB ZE PS PS PM PB PB PB
5 SIMULATION RESULTS
The performance of the proposed algorithm is tested
for the synchronization of two uncertain Lorenz sys-
tems.
The master is defined by:



˙x
1
= α
1
(x
2
− x
1
)
˙x
2
= (−x
1
x
3
+ ρ
1
x
1
− x
2
)
˙x
3
= x
1
x
2
− β
1
x
3
(18)
Synchronization of Uncertain Chaotic Systems using Generalized Predictive Control based on Fuzzy PID Controllers
27

Where x
1
,x
2
,x
3
are the state variables and α
1
,ρ
1
,β
1
are positive uncertain parameters of the system.
And the slave by:



˙y
1
= α
2
(y
2
− y
1
) + u
1
˙y
2
= (−y
1
y
3
+ ρ
2
y
1
− y
2
) + u
2
˙y
3
= y
1
y
2
− β
2
y
3
+ u
3
(19)
Where y
1
,y
2
,y
3
are the state variables , α
2
,ρ
2
,β
2
are
positive uncertain parameters and u
1
,u
2
,u
3
are the
GPC based on fuzzy PI+D or fuzzy PD+I controller.
The synchronization errors are defined as:



e
1
= y
1
− x
1
e
2
= y
2
− x
2
e
3
= y
3
− x
3
(20)
And the error states as:



˙e
1
= α
2
(y
2
− y
1
) − α
1
(x
2
− x
1
) + u
1
˙e
2
= ρ
2
y
1
− y
2
− y
1
y
3
− ρ
1
x
1
+ x
2
+ x
1
x
3
+ u
2
˙e
3
= y
1
y
2
− β
2
y
3
− x
1
x
2
+ β
1
x
3
+ u
3
(21)
To synchronize these chaotic systems ,we chose
the following optimal index:
J
m
(k) =
∑
3
i=−1
[e
m
(k − i)]
2
+ λ
∑
3
j=0
[∆u
m
(k − j)]
2
(22)
Where λ = 0.001.
The one-step predictor of the error states is given
as:
e
m
(k + 1) = 0.9497e
m
(k) + 0.0141e
m
(k − 1)
+0.6806e
m
(k − 2) + 0.6440e
m
(k − 3)
+0.051u
m
(k − 1)
(23)
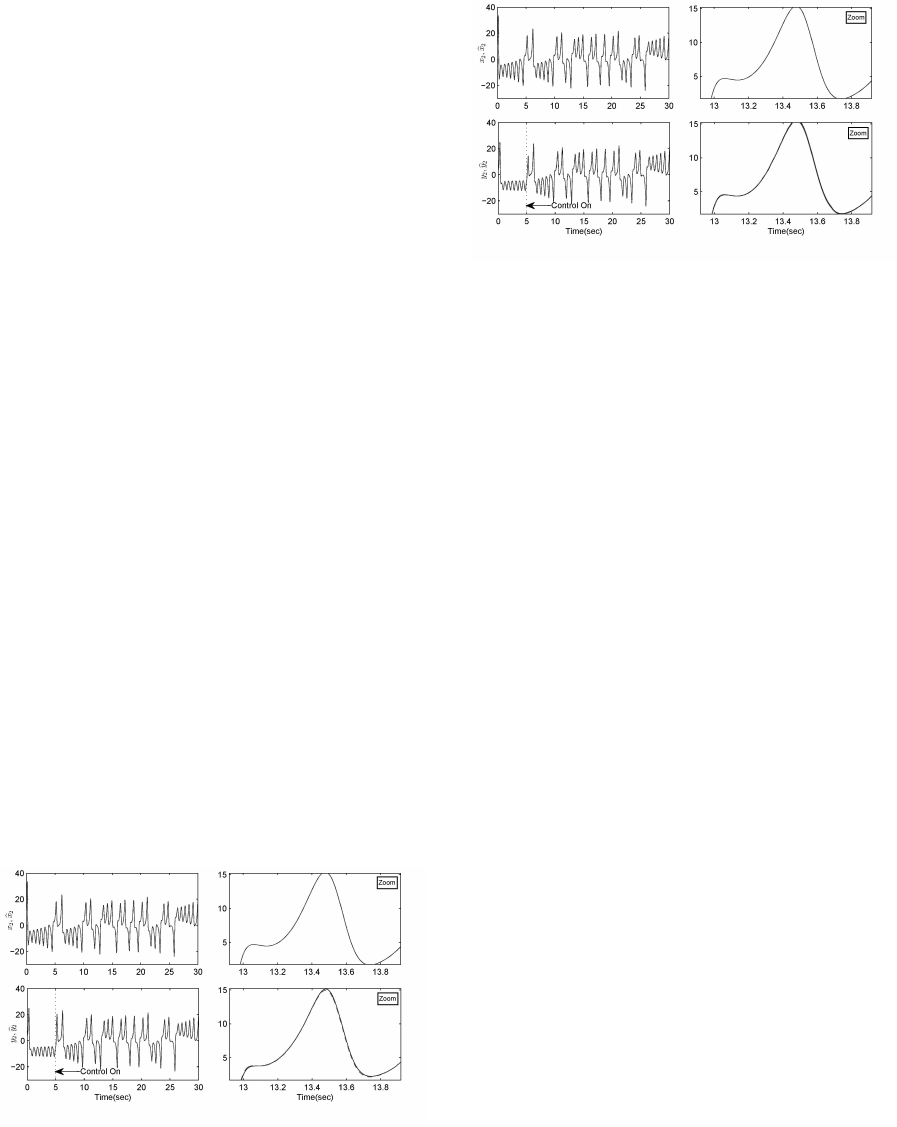
Figures 3 and 4 show the one step predictors of the
states x
2
, y
2
, and their prediction errors.
Figure 3: One step predictors of the states x
2
,y
2
using PI+D
controller.
For the numerical simulation, the parameters of
the master and the slave systems are chosen respec-
tively as:
Figure 4: One step predictors of the states x
2
,y
2
using PD+I
controller.
α
1
= 10,ρ
1
= 28,β
1
= 8/3,
α
2
= 10.5,ρ
2
= 25,β
2
= 8/3 + 0.2
The initial conditions of the master and the slave
systems are taken as :
x
1
(0) = 2, x
2
(0) = 10, x
3
(0) = −6,
y
1
(0) = −2, y
2
(0) = 5, y
3
(0) = 1
In the first part of the simulation, we present
two results obtained using fuzzy PD+I controller.
One with prediction terms and the other with-
out. The parameters of the fuzzy PD+I are chosen
as:K
p
= 1.014,K
d
= 0.594,K
upd
= 0.1,K = 1,K
i
=
2.045,K
ui
= 0.1,L = 30.
In the second part, fuzzy PI+D controller is used
instead of fuzzy PD+I controller. The parameters of
the fuzzy PI+D controller are set: L = 30, Ku
PI
=
1,K
I
= 1,K
P
= 1,K
uD
= 0.001,K
D
= 1.
Figure 5 and Figure 6 show the results of the syn-
chronization of the two systems and the variations of
the cost functions without prediction terms and with
prediction terms respectively for the first case, while
Figure 7 and Figure 8 give the results for the second
case.
For the first case, we can notice that in the absence
of prediction terms, the synchronization between the
two systems is destroyed, and the cost functions take
huge values. However, in the presence of the predic-
tion terms, the synchronization is achieved and the
cost functions converge to zero.
For the second case, the synchronization between
the two systems is achieved with and without predic-
tion terms.
Table 2 summarizes all the results obtained by the
two controllers with and without prediction terms. In
the case of fuzzy PD+I controller, one-step predic-
tion terms ensure the synchronization between the
two systems. However, with the fuzzy PI+D con-
troller, they make a noise and reduce the performance
of the controller. Moreover, the performance of fuzzy
PI+D controller is better than the fuzzy PD+I con-
troller in the two cases. The table shows also that the
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
28

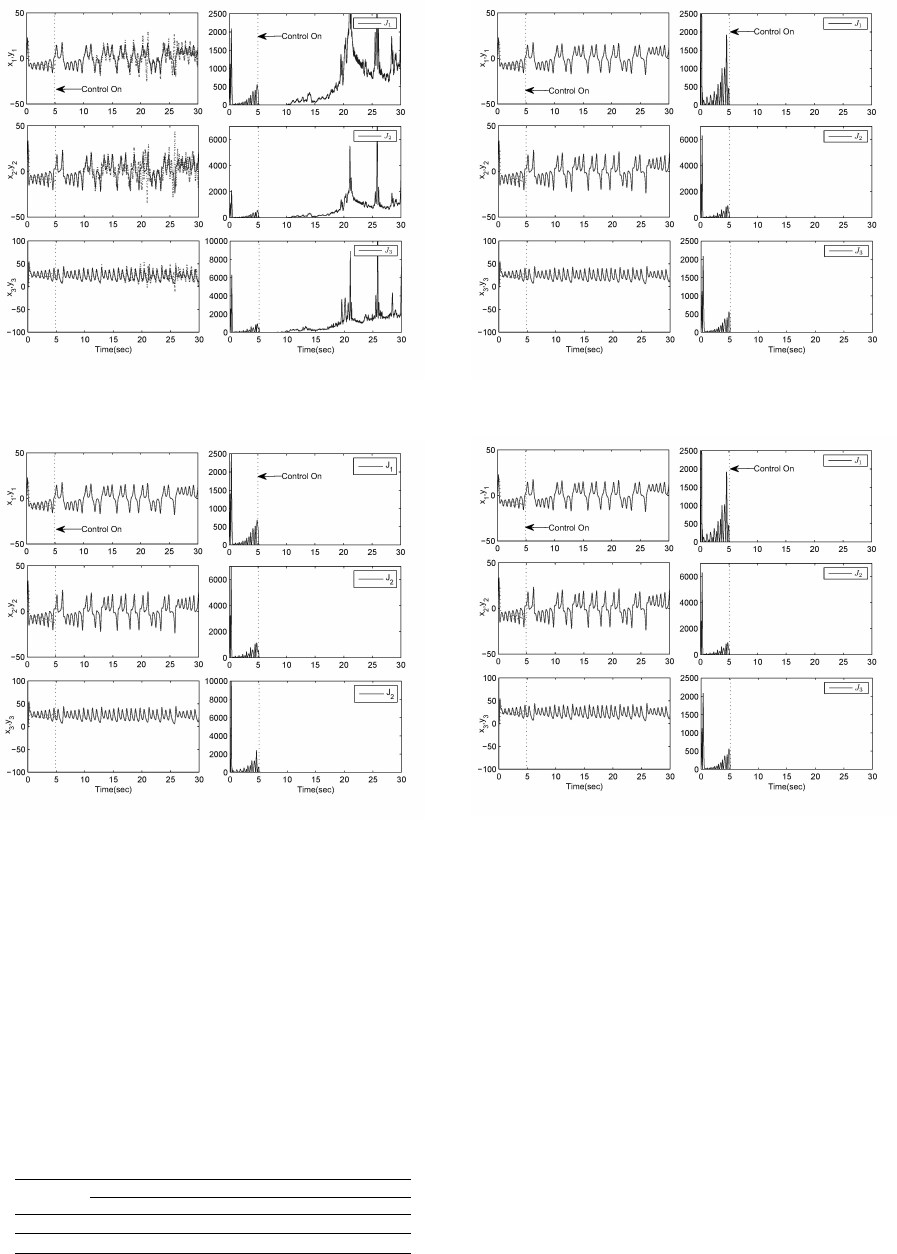
Figure 5: Synchronization of the Lorenz systems and cost
functions variations without prediction terms using fuzzy
PD+I controller.
Figure 6: Synchronization of the Lorenz systems and cost
functions variations with prediction terms using fuzzy PD+I
controller.
prediction terms worsen the results, and this can be
explained by: the modeling error which is considered
as perturbation terms added to the cost functions, the
unpredictability behavior of chaotic systems, or the
structure of the proposed control method which may
need improvements. Although the structure of the al-
gorithm is simpler than many others (Yan and Wang,
2012; Wang and Sun, 2010; Song et al., 2007; Causa
et al., 2008; Mercieca and Fabri, 2011), the role of the
prediction is still questionable.
Table 2: Synchronization and cost function errors.
Without prediction terms With prediction terms
PD+I PI+D PD+I PI+D
∑
3
m=1
e
m
1.1 10ˆ5 60.8 1092.9 89.09
∑
3
m=1
e
Jm
2.15 10ˆ7 285.11 6486.7 3699.6
Figure 7: Synchronization of the Lorenz systems and cost
functions variations without prediction terms using fuzzy
PI+D controller.
Figure 8: Synchronization of the Lorenz systems and cost
functions variations with prediction terms using fuzzy PI+D
controller.
6 CONCLUSION
In this paper, we use generalized predictive control
based on fuzzy PID controllers for synchronization
of uncertain chaotic systems. The synchronization,
between the two systems, is achieved without math-
ematical complexities and by using fuzzy PID con-
trollers, which serve as an optimizer. generalized pre-
dictive control based on fuzzy PID controllers has
a negative and a positive aspect. The positive as-
pect, which concerns fuzzy PD+I controller, appears
when the controller cannot ensure the synchroniza-
tion. In this case, one step ahead prediction term helps
to ensure asymptotic stability, which obviously leads
to reduce the cost function value. However, when
Synchronization of Uncertain Chaotic Systems using Generalized Predictive Control based on Fuzzy PID Controllers
29

a stronger controller is used instead, as an example
fuzzy PI+D controller. The prediction term causes a
negative action and enlarges the synchronization and
the cost function error.
REFERENCES
Causa, J., Karer, G., N
´
unez, A., S
´
aez, D.,
ˇ
Skrjanc, I., and
Zupan
ˇ
ci
ˇ
c, B. (2008). Hybrid fuzzy predictive control
based on genetic algorithms for the temperature con-
trol of a batch reactor. Computers & chemical engi-
neering, 32(12):3254–3263.
Clarke, D. W., Mohtadi, C., and Tuffs, P. (1987). General-
ized predictive controlpart i. the basic algorithm. Au-
tomatica, 23(2):137–148.
Dumur, D. and Boucher, P. (1994). Predictive control appli-
cation in the machine tool field. Advances in Model-
Based Predictive Control, Oxford University Press,
Oxford, pages 471–482.
Jin-quan, H. and Lewis, F. L. (2003). Neural-network pre-
dictive control for nonlinear dynamic systems with
time-delay. Neural Networks, IEEE Transactions on,
14(2):377–389.
Lam, H. and Leung, F. F. (2006). Synchronization of uncer-
tain chaotic systems based on the fuzzy-model-based
approach. International Journal of Bifurcation and
Chaos, 16(05):1435–1444.
Lam, H.-K. and Seneviratne, L. D. (2007). Synchroniza-
tion of chaotic systems using neural-network-based
controller. International Journal of Bifurcation and
Chaos, 17(06):2117–2125.
Lu, J., Chen, G., and Ying, H. (2001). Predictive fuzzy pid
control: theory, design and simulation. Information
Sciences, 137(1):157–187.
Mercieca, J. and Fabri, S. (2011). Particle swarm optimiza-
tion for nonlinear model predictive control. In ADV-
COMP 2011, The Fifth International Conference on
Advanced Engineering Computing and Applications
in Sciences, pages 88–93.
Song, Y., Chen, Z., and Yuan, Z. (2007). New chaotic
pso-based neural network predictive control for non-
linear process. Neural Networks, IEEE Transactions
on, 18(2):595–601.
Sun, Z., Zhu, W., Si, G., Ge, Y., and Zhang, Y. (2013).
Adaptive synchronization design for uncertain chaotic
systems in the presence of unknown system parame-
ters: a revisit. Nonlinear Dynamics, 72(4):729–749.
Tang, K., Man, K. F., Chen, G., and Kwong, S. (2001). An
optimal fuzzy pid controller. Industrial Electronics,
IEEE Transactions on, 48(4):757–765.
Wang, X. and Xiao, J. (2005). Pso-based model predictive
control for nonlinear processes. In Advances in Natu-
ral Computation, pages 196–203. Springer.
Wang, Z. and Sun, Y. (2010). Generalized predictive con-
trol based on particle swarm optimization for lin-
ear/nonlinear process with constraints. In Computa-
tional Intelligence and Natural Computing Proceed-
ings (CINC), 2010 Second International Conference
on, volume 1, pages 303–306. IEEE.
Yan, Z. and Wang, J. (2012). Model predictive control of
nonlinear systems with unmodeled dynamics based on
feedforward and recurrent neural networks. Industrial
Informatics, IEEE Transactions on, 8(4):746–756.
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
30