
Does ‘Merging DEMO Models’ Satisfy the Associative Law?
Validation of Partial Models and Merge Operation
Tetsuya Suga and Junichi Iijima
Graduate School of Decision Science and Technology, Tokyo Institute of Technology, Meguro-ku, Tokyo, Japan
Keywords:
Enterprise Ontology, Business Process Modeling, Formalization, Algebra, Set Theory, DEMO.
Abstract:
Partial models are small models produced by splitting a large full model into meaningful conceivable-sized
fragments with each separate diagram. They are commonly used when the full model is too large and shared by
several people who have their own scope of interest. Those partial models are subject to being manipulated—
merged for instance. This context calls for discussion in Enterprise Ontology (EO) about the capability of
business process modeling languages in handling partial models and manipulations on them. There, indeed,
exists a lack of researches in the methodology of EO, namely Design & Engineering Methodology for Or-
ganizations (DEMO) for formal studies on its consistency in producing partial models and merging them. It
stems from a deficiency of formal semantics in the specification of the notation. By formalizing the DEMO
Construction Model (CM) with a concept of well-formed models and the merge operation from a set-theoretic
approach, this paper clarifies that the closedness, commutativity, and associativity are guaranteed in merging
partial models of DEMO CM. An example of EU-Rent accompanies the formalizations for validation and
demonstration.
1 INTRODUCTION
Since human beings began to practice the division of
labor, business processes extend over several opera-
tional units within an organization or even over multi-
ple organizations, and consist of many activities per-
formed by different persons. In such a situation, one
overall process model can be shared by several peo-
ple who have their own specialized area, hence have
a different scope of interest in the model. At the same
time, as modern society has grown more sophisticated
and complicated, the scope required to be covered in
process models also becomes larger, sophisticated and
complicated.
Enterprise Engineering (EE) is an emerging re-
search discipline that pursues better understandings
and implementations from the perspective of engi-
neering. Among three domains
1
of EE, Enterprise
Ontology studies an understanding—in other words,
modeling—of the operation in enterprises as entirely
independent of their realization and implementation.
This characteristic contributes for challenging the
problem in modern society.
The general trend mentioned in the first paragraph
1
Enterprise Ontology (EO), Enterprise Architecture
(EA), and Enterprise Governance.
makes it necessary to take an arbitrary part of an over-
all model for generating a partial model—splitting
the large overall model into meaningful conceivable-
sized fragments with each separate diagram (also re-
ferred to as modularizing and decomposing). For ex-
ample, given a business process model of a supply
chain as an overall model, the sales manager hopes
to have a partial model focused on processes between
stores and warehouses while the procurement man-
ager would like to focus on processes between sup-
pliers and assembly factories (see Figure 1). Some-
times it is done for the sake of simplicity and under-
standability throwing away things out of interest, and
sometimes for serious practical concerns that models
are too large to print on a single sheet of paper. In
addition to just deriving partial models, those partial
models are subject to being manipulated—merge,
match, diff, split, slice, etc.—for various purposes.
During these manipulations, the syntactic, notational
or grammatical correctness, validity, consistency, you
name it on the manipulations are usually reserved by
decent efforts and considerations of experienced ex-
perts.
Problem Definition and Motivation
This context reinforces discussions for each modeling
Suga, T. and Iijima, J..
Does ‘Merging DEMO Models’ Satisfy the Associative Law? - Validation of Partial Models and Merge Operation.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 2: KEOD, pages 467-478
ISBN: 978-989-758-158-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
467

language on the handleability in handling partial mod-
els and operations on the domain of partial models,
as one of the characteristics of modeling languages
themselves. Desirable modeling languages should be
less likely to cause inconsistency when users produce
partial models and manipulate them.
The following high-school-level example may fig-
ure out the meaning of “the handleability in handling
partial models and operations on the domain of par-
tial models”. Let’s say one plus two equals three
(1 + 2 = 3). Suppose that the domain is the natural
numbers 1, 2, 3, ... (N). Then, plus is an operation on
the domain N and the result three is a natural num-
ber. In general, if you apply the operation plus to two
natural numbers, the result is a natural number and
never become a number out of the domain (formally
∀n, m ∈ N, n + m ∈ N; closedness). You can change
the order like 1 + 2 = 2 + 1 (commutativeness). If
you however say one minus two equals minus one
(1 − 2 = −1), the situation has been changed. The
result minus one is not a natural number. You can-
not change the order like 1 − 2 6= 2 − 1 because of
1−2 = −1 and 2−1 = 1. However, if you replace the
domain with the integers ..., −3, −2, −1, 0, 1, 2, 3, ...
(Z), the result minus one is an integer and thus still
remains in the domain. Although you solved the trou-
ble in closedness, you still cannot change the order.
Therefore, whether operations have properties such as
closedness and commutativeness or not depends on
how you define the domain (N, Z, etc.) and the opera-
tions (addition plus, subtraction minus, multiplication
times, division divide, etc.). This paper will define a
domain and an operation as well.
Let us go back to the original topic. As a method-
ology of EE, this paper assumes and follows De-
sign & Engineering Methodology for Organizations
(DEMO). DEMO is said to be coherent, consistent,
comprehensive and essential methodologies, show-
ing an organization as a network of responsibilities
Figure 1: Image of Problem.
and interactions. A DEMO model is a compact yet
complete model representing “who is responsible for
what”. It focuses only on the ontological aspect of the
organization, resulting in giving insight and overview
of the organization. DEMO has four aspect mod-
els such as Construction Model (CM) at the top with
the highest abstraction, Process Model (PM), Action
Model (AM) and Fact Model (FM).
As DEMO is designed to be consistent, the au-
thors feel—other DEMO users might likely agree
with—solid thoughts that there is less opportunity
to encounter inconsistency when generating partial
models and manipulating them in DEMO models dur-
ing past practical projects. However, some questions
may arise:
Q1: What are the requirements for generating
an appropriate partial model from the overall
model?
Q2: Is there any possibility to produce a broken
model (a model which does not follow the correct
syntax) when merging two partial models? i.e.
closedness
Q3: Does the order of merging matter?
i.e. commutativity: X+Y
?
= Y+X and associativity:
(X+Y)+Z
?
= X+(Y+Z)
The motivation of this study is to answer these ques-
tions with formal reasoning.
Related Works
Several papers have addressed the problem about
ways to manage large models efficiently and effec-
tively: handling partial models and manipulating
them with issues of consistency. In recent works,
(Enjo et al., 2010) studied this problem on UML Class
Diagram, and (Liepins et al., 2012) on Web Ontology
Language. (Mancioppi et al., 2012) discussed clas-
sifications for fragmentation techniques and common
rationale stories on the scene.
To the best of the authors’ knowledge, formal-
ization of DEMO Construction Model (CM) has not
been studied very well. Although DEMO Process
Model (PM) has been formalized in Petri Net, it
seems difficult to extend the formalization to CM be-
cause CM does not have the concept of states and
transitions which Petri Net stands on. Although for-
mal descriptions for the meta-model for CM have
been presented on occasion, ones for CM itself are
very few except the CRISP model and crispienets ex-
plained in (Dietz and Hoogervorst, 2014). However,
there still exists a lack of research on a formalization
of CM which enables to answer the questions above.
Even if people share a consensus on the consistency
SSEO 2015 - Special Session on Enterprise Ontology
468

of DEMO model, it is not trivial and nothing guaran-
tees the consistency.
Purpose Statement
While the lack does not matter if the scope of model-
ing is enough small for persons to understand, this is-
sue will become tangibly critical especially when the
scope of modeling becomes complex or large verti-
cally (depth; granularity) and/or horizontally (width)
beyond the capabilities of human beings. As stud-
ies of EE and DEMO advanced, the targets (ob-
jects) of modeling have been more practical, large,
and complex–from small fictional models with a few
transactions such as a pizza shop and library, to large
practical models with more than ten transactions such
as (Op’t Land et al., 2009). Moreover, the issue will
become more important when those manipulations
are performed by inexperienced persons or executed
automatically by computer codes. In fact, there have
been some active studies to handle DEMO models
and execute them such as DEMO engine (van Kervel,
2011).
The significance of this study for EE and DEMO
is to provide to the notation of DEMO models a for-
mal semantics that enables to formally define and
analyze the models. Such a formal representation
grounded on mathematical notations describes the
properties of the models in a precise way and brings a
high abstraction which help with answering the ques-
tions with context-independent explanations, unlike
ambiguous natural languages and diagrams. Once the
model is copied down into mathematical formulae,
proves goes by themselves within mathematical laws.
This is supported by soundness and completeness of
logic, which insist that “anything one can prove is se-
mantically valid” and “any argument that is semanti-
cally valid is derivable”.
The purpose of this study is to examine the struc-
ture of DEMO in formalism and to reveal formal ra-
tionales behind its consistency. Developing the for-
mal descriptions of DEMO and operations on the
models will answer the questions above. The remain-
der of this paper is compromised as follows: Sec-
tion 2 presents related studies and basics of DEMO
Construction Model (CM) to compose the research
methodology for this paper explained in Section
3. Section 4 describes the formal representation of
DEMO CM with a concept of sub-model. Finally,
Section 5 defines the merge operation on the models
and reveals crucial theorems of its closedness, com-
mutativity, and associativity as the primary contribu-
tion of this study. Section 6 discusses the result of this
paper, leading to the conclusion in Section 7. From
Section 4 through 6, a common example of EU-Rent
accompanies the formalizations for the validation and
demonstration.
2 LITERATURE REVIEW
As mentioned in section 1, mappings between the
Process Model (PM) and Petri Net have been stud-
ied. However, it does not rise above the level of Pro-
cess Mode because Construction Model (CM) does
not have the concept of states and transitions which
Petri Net stands on. Another part which advances
in formalization is ones at meta-level. Many papers
presented the formal description on occasion often in
terms of information structure. However, there exists
a lack of research on a formalization of CM which
enables to answer the questions above.
Therefore, in this section, the authors present the
structured literature review on formalizations of other
business process models by models and approaches.
This section also includes explanations about basics
of DEMO CM. Combining these two reviews will
work for designing research methodology for a for-
malization of DEMO CM.
2.1 Related Works on Formalization of
Other Modeling Languages
While there exists a variety of modeling languages,
they may be divided into two: flow
2
and non-flow
3
based modeling languages. In the formalism of flow
based modeling languages, the most common ap-
proaches are state-transition-systems such as Petri
Net including Workflow Net, graphs such as Work-
flow Graph, and algebra such as process algebra in-
cluding CSP and general algebra of categories or sets.
These approaches are, however, of no use for for-
malizing DEMO Construction Model (CM) due to its
non-flow based structure
4
. This point requires review-
ing related works especially on non-flow based mod-
eling languages. In this paper, the authors focus on
UML Class Diagrams and UML Use Case Diagrams
because these are ones of the most popular languages
with advanced studies.
2
Workflow and data flow models such as UML Se-
quence Diagram, UML Activity Diagram, BPMN, EPC,
RAD, BPEL, YAWL, DEMO Process Model, etc.
3
For example, UML Class Diagram, UML Use Case Di-
agram, DEMO Construction Model, etc.
4
Some papers, to our surprise, still find out ways to uti-
lize Petri Net for non-flow based diagrams such as (Baresi
and Pezz, 2001) for UML Class Diagram and (Zhao and
Duan, 2009) for UML Use Case Diagram.
Does ‘Merging DEMO Models’ Satisfy the Associative Law? - Validation of Partial Models and Merge Operation
469
(Shroff and France, 1997) adopted Z notation in
Class Diagram for representing classes, associations,
aggregations and generalization structures. (Sengupta
and Bhattacharya, 2006) hired the same approach in
Use Case Diagram.
(Meng and Aichernig, 2003) adopted category
theory with an algebraic approach in Class Diagram
and Use Case Diagram, proposing coalgebraic seman-
tics of classes, associations, and generalization, and
giving an example of consistency checking.
(Enjo et al., 2010) adopted algebraic set theory for
representing classes, associations, and generalizations
with discussions on techniques to keep consistency
and operations (union, intersection, difference, com-
plement) on the algebra.
(Berardi et al., 2001) adopted Description Logic
(DL) in Class Diagram for representing classes, asso-
ciations, aggregations, constraints and generalization.
(Klimek and Szwed, 2010) adopted temporal logic
in Use Case Diagram for representing include, ex-
tends and inheritance relations with verification.
In spite of these diverse studies for UML, DEMO
is short of formalizations.
2.2 DEMO Construction Model
Design & Engineering Methodology for Organiza-
tions (DEMO) is a modeling methodology for an en-
terprise. In an enterprise as the general term refer-
ring to a kind of collaborative activity by human be-
ings, there exists a business referring to the function
perspective and an organization referring to the con-
struction perspective. Compared with other enterprise
modeling languages, DEMO puts more emphasis on
the construction perspective with the language/action
perspective (LAP). It has been developed with scien-
tific and engineering research since the 1980s led by
Jan Dietz at the Delft University of Technology and
other active researchers in CIAO! Network
5
. DEMO
has several characteristic concepts and topics such as
the standard/complete transaction pattern, levels of
abstraction (business-information-data or essential-
informational-documental), four aspects model (Con-
struction Model, Process Model, Action Model, Fact
Model), and the operational principle.
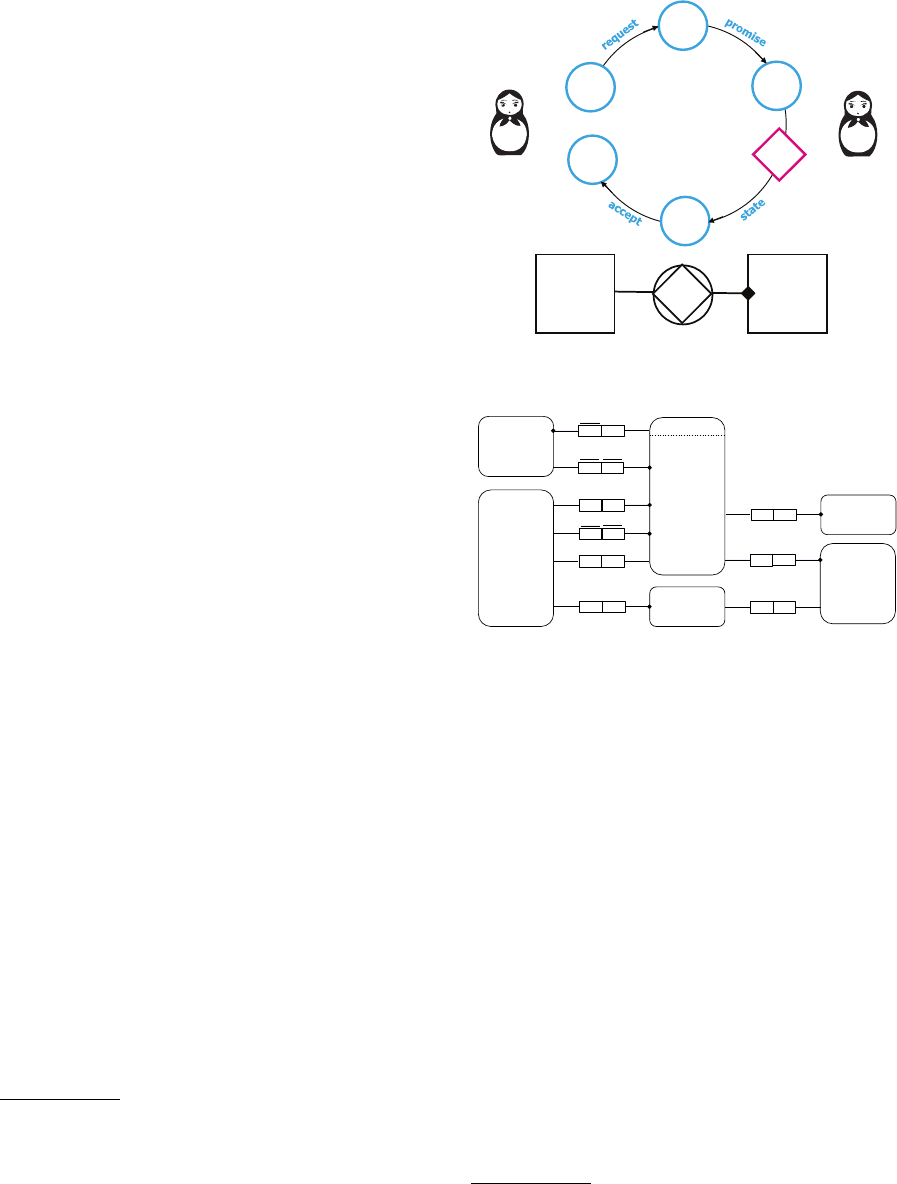
The operational principle in DEMO represents in-
teractions between two parties for a transaction kind
6
5
http://ciaonetwork.org/
6
In DEMO, a transaction and a transaction kind are
distinguished, similar to an object (instance) and a class
in object-oriented programming language such as Java. A
transaction kind is a template, as well as a class is an ex-
tensible template with member variables (for representing
state) and methods (or member functions; implementations
proposition
requested
proposition
promised
result
stated
result
accepted
result
produced
<initial
status>
consumer
pr
oducer
A
k
A
n
T
n
Figure 2: The Operation Principle, Excerpted from (Perin-
forma, 2012).
FACT KIND
ELEMENTARY
ACTOR ROLE
instances of FK are
contained in the bank of TK
transaction sort [SORT]
EAR is an initiator of TK
EAR is the executor of TK
EAR has access to the
bank of TK
COMPOSITE
ACTOR ROLE
FK is the product kind of TK
TK is part of ATK
EAR is hidden in CAR
AGGREGATE
TRANSACTION KIND
ATK is contained in CAR
TRANSACTION KIND
COMPOSITE
ACTOR ROLE
TK is contained in CAR
Figure 3: Meta-Model of DEMO CM, Excerpted from (Di-
etz, 2013).
as follows: when John wants Mary to create a desired
result such as producing something or providing a ser-
vice, John begins communicating to Mary with a re-
quest. The person who is responsible for the results
(here Mary) provides in response to the request to an-
swer a promise. After a certain time when Mary fin-
ishes the work, she will state that the desired result is
achieved. If the person who had asked for the result
(here John) accepts the result, the whole interaction
will be finished. DEMO defines a transaction kind as
the pattern described in the interaction between two
parties, and a business as the chain of transactions.
Among the four aspect models, the Construction
Model (CM) is the ontological model of the construc-
tion of organizations: the composition (inside), the
environment (outside), and the structure. Specifically,
they are consists of the active and passive mutual in-
teractions among the elements in the composition and
such interactions between them and the ones in the en-
vironment. The CM contains the identified actor roles
of operation). For every execution, a transaction kind gen-
erates a new transaction as an instance of the transaction
kind, as well as a class generates a new object of the class.
SSEO 2015 - Special Session on Enterprise Ontology
470
in the composition and in the environment, the iden-
tified transaction kinds between the actor roles in the
scope, and between those and the actor roles in the en-
vironment. Formally, the components of the CM are
shown in the form of meta model in Figure 3. The CM
of an organization is represented with an Organization
Construction Diagram (OCD), a Transaction Product
Table (TPT), and a Bank Contents Table (BCT).
Please refer to (Dietz, 2006; Perinforma, 2012;
Dietz, 2012; Dietz, 2013) for EO and DEMO.
3 RESEARCH METHODOLOGY
3.1 Choice of Approach
According to literature review on formalizations of
other modeling languages, the following approaches
may works: Z notation, set algebra, category algebra,
Description Logic, temporal logic and Petri Net.
Z notation has been developed by the Program-
ming Research Group (PRG) in Oxford University
as a formal specification language for describing and
modeling software and computer-based systems. As
template-like schema notations to show the structure
of specifications, It uses well-defined types (set, se-
quences, relations, functions) and defines operations
by showing pre/post states. Z tackles the problem
that large specifications reduces the readability and
manageability if using mathematics alone. Besides
these advantages, Z may bring the barrier of the no-
tation. In addition, while formalizing models by Z
is pretty common, there seem no tentative attempts
beyond formalization to examine algebraic properties
of the operations on it as also addressed in (Moreira
et al., 2004). This point leads to abstaining from em-
ploying Z notation for this study.
Temporal logic is a system of rules and symbol-
ism for coping with propositional logic with the con-
cept of time. Since DEMO CM does not include the
concept of time or sequence, temporal logic will not
perform well.
Description Logics (DL) is one of the formal
knowledge representation languages. It is more pow-
erful than propositional logic and first-order predicate
logic in expressiveness and decidability of reasoning
problems. Despite its expressiveness, DL has very
few previous studies on operations on models.
Category theory is a mathematical theory for a
collection of objects and of arrows (relations) to the
study of algebraic structure, favored by computer sci-
entists. Set theory is the mathematical theory of col-
lections of objects. Discussions on differences be-
tween categorical and set-theoretic foundations are so
complicated that this paper shall reserve the explana-
tion for other materials. Within this paper, it is enough
to say that set theory focuses on objects while cate-
gory theory focuses not on objects but on the relations
between the objects (morphisms). Practically, cate-
gory theory is highly sophisticated realm while set
theory is comprehensible at the undergraduate level
mathematics.
Among these formalizations, it turns out that the
algebraic specification with set theory is most suited
for this study due to its low barrier of the notation and
concepts, and its past results for studying operations
on the formalization in (Enjo et al., 2010).
3.2 Procedures
Starting the construction of formalizations, this study
was conducted along with the steps following (Enjo
et al., 2010)’s work on UML Class Diagrams.
1. Enumerate basic components of DEMO CM and
formalize them in the mathematical language
(Section 4.1).
2. Figure out relationships and requirements among
the components in OCD, and then representing
them using formulae (Section 4.2).
3. Define the concept of partial models in OCD with
discussions of its properties (Section 4.3).
4. Define the merge operation on OCD with discus-
sions of its remarkable theorems (Section 5).
3.3 Assumptions and Scope
For the sake of refined simplicity, this study assumes
the following limitations.
Assumption 1. Only actor roles and transaction
kinds are considered, excluding aggregate transaction
kinds
Assumption 2. Only initiator links and executor links
are presented, excluding information links among
three link types
Assumption 3. Only a single initiator link for each
transaction kind
4 FORMALIZATION OF OCD
This section prepares formal definitions of DEMO
CM for this study. Along with formal definitions, this
paper shows an example of EU-Rent (Figure 4) that
is originally taken from (Open Management Group,
2013).
Does ‘Merging DEMO Models’ Satisfy the Associative Law? - Validation of Partial Models and Merge Operation
471
A3
car
issuer
T1
T2
A1
rental
starter
A2
rental
ender
T5
T3
T4
CA1
renter
CA3
payer
CA2
driver
rental start
rental end
rental payment
car pickup
car drop off
Figure 4: OCD of EU-Rent, Excerpted from (Dietz, 2012).
Please note that this paper distinguishes corre-
sponding terms depending on whether they are used
in the context of practice or that of formalization.
Practice Formalization
partial model sub-model
manipulation operation
merge union
4.1 Formal Definition of Components in
DEMO CM
Definition 1 (Society). A society is comprised of ac-
tor roles and transaction kinds. Let ActorRole be a
set of actor roles and Transaction a set of transaction
kinds. Then a society is described as a couple:
Society =
h
ActorRole, Transaction
i
Definition 2 (Actor Role Identification). An ac-
tor role a has the following three mappings
as its properties. In other words, actor roles
are identified/characterized as a triple (3-tuple)
( f
ARtype
(a), f
ARno
(a), f
ARname
(a)):
1. ActorRole type operator
f
ARtype
: ActorRole → ARtype
is a mapping from an actor role to one of the types
of actor role ARtype =
{
elementary, composite
}
or in short ARtype =
{
E,C
}
.
2. ActorRole number operator
f
ARno
: ActorRole → N
0
is a mapping from an actor role to a non-negative
integer N
0
, which includes zero.
3. ActorRole name operator
f
ARname
: ActorRole → string
is a mapping from an actor role to a string
7
.
7
Let an alphabet Σ be a finite set of symbols (normally
used in a natural language). A string over the alphabet Σ
is a finite sequence of symbols from Σ. ‘A set of strings in
Σ’ Σ
?
can be recursively defined by Λ ∈ Σ
?
and x ∈ Σ ∧ s ∈
Σ
?
⇒ xs ∈ Σ
?
(where Λ is the empty string).
Definition 3 (Transaction Kind). A transaction kind t
is an element of ActorRole × ActorRole, where × de-
notes the Cartesian product (direct product). A trans-
action kind can be described as t = (a, a
0
). In DEMO,
actor role a (and a
0
) is called an initiator (executor),
respectively.
Definition 4 (Transaction Kind Identification). A
transaction kind t has following four mappings as
its properties. In other words, transaction kinds
are identified/characterized as a quadruple (4-tuple)
( f
T no
(t), f
T name
(t), f
Tin
(t), f
Tex
(t)):
1. Transaction kind number operator
f
T no
: Transaction → N
+
is a mapping that assigns a positive integer for
each transaction kind.
2. Transaction kind name operator
f
T name
: Transaction → string
is a mapping from a transaction kind to a string.
3. Transaction kind initiator/executor operator
f
Tin
: Transaction → ActorRole
f
Tex
: Transaction → ActorRole
is a mapping from a transaction kinds to an actor
role which is an initiator/executor of the transac-
tion kind. Those operators extract the first/second
operand of Cartesian product in Definition 3.
Example 1. In our society, there exists many actor
roles and transaction kinds. EU-Rent is just a small
part of the society. From them, modelers define the
scope of interest—EU-Rent here. This situation is
shown in Figure 5.
(
Transaction =
{
. . . , t
1
, t
2
, t
3
, t
4
, t
5
, . . .
}
ActorRole =
{
. . . , a
0
, a
1
, a
2
, a
3
, a
4
, a
5
, . . .
}
Mapping of operators are shown in Table 1.
Table 1: Mappings of the Example.
a f
ARtype
f
ARno
f
ARname
t f
T no
f
T name
f
Tin
f
Tex
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
0
C 1 renter t
1
1 rental start a
0
a
1
a
1
E 1 rental starter t
2
2 rental end a
0
a
1
a
2
E 2 rental ender t
3
3 car pick up a
4
a
3
a
3
E 3 car issuer t
4
4 car drop off a
3
a
4
a
4
C 2 driver t
5
5 rental payment a
2
a
5
a
5
C 3 payer
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SSEO 2015 - Special Session on Enterprise Ontology
472
Society
EU-Rent
A3
car
issuer
T1
T2
A1
rental
starter
A2
rental
ender
T5
T3
T4
CA1
renter
CA3
payer
CA2
driver
rental start
rental end
rental payment
car pick up
car drop off
a
0
a
1
a
3
a
2
a
4
a
5
t
1
t
2
t
5
t
3
t
4
Figure 5: Society =
h
ActorRole, Transation
i
.
4.2 Formal Definition of OCD
Definition 5 (Organization Construction Diagram).
Suppose that A is a subset of ActorRole (i.e. A ⊆
ActorRole) and T is a subset of Transaction (i.e.
T ⊆ Transaction). Then a couple (2-tuple)
h
A, T
i
which satisfies the following conditions is called an
OCD.
h
A, T
i
∈ 2
ActorRole
× 2
Transaction
Condition 1 (Unique Actor Role Name Axiom). If
names of two actor roles are equal, those two actor
roles are the same.
∀a
i
, ∀a
j
∈ A, ( f
ARname
(a
i
) = f
ARname
(a
j
) ⇒ a
i
= a
j
)
Condition 2 (Unique Transaction Kind Name Ax-
iom). If names of two transaction kinds are equal, two
transaction kinds are equal.
∀t
i
, ∀t
j
∈ T, ( f
T name
(t
i
) = f
T name
(t
j
) ⇒ t
i
= t
j
)
Condition 3 (Numbering Axiom). The executor of a
transaction kind gets the same number as the transac-
tion kind (“a very practical convention”)
∀t ∈ T, f
ARno
( f
Tex
(t)) = f
T no
(t)
Condition 4 (Closed OCD Axiom for Actor Role).
All of the actor roles responsible for a transaction kind
are included in the set of actor roles of the OCD. Sup-
pose
h
A, T
i
is an OCD, then:
∀t ∈ T, ∀a ∈ ActorRole,
a ∈ f
Tin
(t) ∪ f
Tex
(t) ⇒ a ∈ A
Condition 5 (Actor Role Participation Axiom). For
every actor role in the OCD, there is at least one trans-
action kind such that the actor role participates. Sup-
pose
h
A, T
i
is an OCD, then:
∀a ∈ A, ∃t ∈ T, a ∈ f
Tin
(t) ∪ f
Tex
(t)
4.2.1 Related Operator
Definition 6 (Actor Role Closure for Transaction
Kind). Let T be a subset of transaction kinds (i.e.
T ⊆ Transaction). Actor role closure operator
γ: 2
Transaction
→ 2
ActorRole
is a mapping from a set of transaction kinds to a set of
related actor roles.
γ(T ) =
{
a ∈ ActorRole
|
∃t ∈ T, a ∈ f
Tin
(t) ∪ f
Tex
(t)
}
=
S
t∈T
( f
Tin
(t) ∪ f
Tex
(t))
Example 2. Let EU-Rent be
h
A, T
i
, where A =
{
a
0
, a
1
, a
2
, a
3
, a
4
, a
5
}
and T =
{
t
1
, t
2
, t
3
, t
4
, t
5
}
. In this
case:
γ(T ) =
{
a
0
, a
1
, a
2
, a
3
, a
4
, a
5
}
4.3 Sub-society and Sub-OCD
In algebra, it is very common to single out from an ar-
bitrary algebraic structure containing a distinguished
subset, such as affine spaces and subspaces of vector
spaces, sub-groups of groups, ideals and sub-rings of
rings, sub-fields of fields, and so on. If intuitively gen-
eralized, these subsets are characterized to be closed
under some algebraic operations defined on the struc-
ture. This section introduces the notion of sub-OCD
and describes that any sub-OCDs satisfy some condi-
tions tautologically.
4.3.1 A Family of Sub-societies
Before defining sub-OCDs, a family of sub-Societies
is defined as follows.
Definition 7 (Sub-Society). Given an OCD
h
A
◦
, T
◦
i
where A
◦
⊆ ActorRole and T
◦
⊆ Transaction, the
OCD
h
A
◦
, T
◦
i
can bring about ‘a family of sub-
Societies’ D of
h
A
◦
, T
◦
i
as below.
D ⊆
{
(A, T )
|
A ⊆ A
◦
, T ⊆ T
◦
}
For the sake of readability, this paper hires the next
expression for D which is equivalent the above.
D ⊆ 2
A
◦
× 2
T
◦
D is called “a family of sub-Societies” or “sub-
Societies”.
Please note that some members of a family of
sub-Societies may not be an OCD, not satisfying all
the conditions that OCDs must satisfy. At this point,
these sub-models are “naive” in the sense that they are
brought just by selecting some of the elements with-
out considering further requirements, as claimed in
the next proposition.
Does ‘Merging DEMO Models’ Satisfy the Associative Law? - Validation of Partial Models and Merge Operation
473
Proposition 1 (Partial Preservation of Sub-Societies).
If a given
h
A
◦
, T
◦
i
is an OCD, every member of the
sub-Societies D ⊆ 2
A
◦
×2
T
◦
satisfies following condi-
tions:
• Condition 1: Unique Actor Role Name Axiom
• Condition 2:
Unique Transaction Kind Name Axiom
• Condition 3: Numbering Axiom
From now on, unfolded proofs for theorems,
propositions, and lemmas are placed in the appendix
for readability.
4.3.2 Sub-OCDs
As mentioned in the first paragraph of this chapter,
one of the motivations to consider sub-OCDs is to
make the sub-OCDs closed under some algebraic op-
erations defined on the structure. The following def-
inition imposes further conditions onto the “naive”
sub-Societies.
Definition 8 (Sub-OCD). Given a family of sub-
Societies D of OCD
h
A
◦
, T
◦
i
, it is possible to orga-
nize ‘the family of sub-OCDs’ of D by selecting sub-
Societies that satisfy the rest two conditions of the
five conditions from D. D
?
denotes the family of sub-
OCDs obtained by D.
• Condition 4: Closed OCD Axiom for Actor Role
• Condition 5: Actor Role Participation Axiom
Required conditions above are the same of the orig-
inal OCD. Please note that no further considera-
tions are needed. From now, the rest of this section
prepares equivalent expressions of the conditions to
make proofs simpler.
Lemma 1 (Another Expression of Condition 4). Let
h
A
◦
, T
◦
i
be an OCD. Then, for a family of sub-
Societies D ⊆ 2
A
◦
× 2
T
◦
, Condition 4 ‘Closed OCD
Axiom for Actor Role’ is the same as the following
condition.
∀
h
A, T
i
∈ D, γ (T ) ⊆ A
One can interpret this as meaning that for every OCD
in the family of sub-OCDs, all of the actor roles that
get involved with all of the transaction kinds of the
OCD must be included in the actor roles of the OCD.
Lemma 2 (Another Expression of Condition 5). Let
h
A
◦
, T
◦
i
be an OCD. Then, for a family of sub-
Societies D ⊆ 2
A
◦
×2
T
◦
, Condition 5 ‘Actor Role Par-
ticipation Axiom’ is the same as the following condi-
tion.
∀
h
A, T
i
∈ D, A ⊆ γ (T )
Remark 1 (Full Preservation of Sub-OCDs). Every
member of a family of sub-OCDs D
?
⊆ 2
A
◦
×2
T
◦
is an
OCD. Among the five conditions to be an OCD, Con-
dition 1, 2 and 3 are delivered from the characteristics
of sub-Societies by Theorem 1 while the remaining
condition 4 and 5 are imposed by Definition 8. Please
note that “naive” sub-Societies do not always satisfy
all the five conditions.
Example 3. Let us take OCD
h
A
◦
, T
◦
i
as the whole
of EU-Rent, an instance of D is:
D =
h{
a
0
, a
1
, a
2
, a
4
}
,
{
t
2
, t
3
, t
4
, t
5
}i
,
h{
a
0
, a
1
, a
2
}
,
{
t
1
, t
2
}i
,
h{
a
0
, a
1
, a
3
, a
4
}
,
{
t
1
, t
3
}i
,
h{
a
0
, a
2
, a
3
, a
4
, a
5
}
,
{
t
2
, t
4
, t
5
}i
⊆ 2
A
◦
× 2
T
◦
Since
h
A
◦
, T
◦
i
satisfies Condition 1, 2 and 3, every
element of D satisfies these three conditions too as
trivially confirmed.
Now let’s check one by one whether the elements
of D are sub-OCDs or not.
• A
0
=
{
a
0
, a
1
, a
2
, a
4
}
, T
0
=
{
t
2
, t
3
, t
4
, t
5
}
T2
A1
rental
starter
A2
rental
ender
T5
T3
T4
CA1
renter
CA2
driver
rental end
rental payment
car pick up
car drop off
Figure 6:
h
A
0
, T
0
i
.
h
A
0
, T
0
i
is a sub-Society, but not a sub-OCD be-
cause
h
A
0
, T
0
i
does not satisfy Condition 4 via
Lemma 1 or Condition 5 via Lemma 2 :
γ(T
0
) =
{
a
0
, a
2
, a
3
, a
4
, a
5
}
* A
0
A
0
= {a
0
, a
1
, a
2
, a
4
} * {a
0
, a
2
, a
3
, a
4
, a
5
}
• A
1
=
{
a
0
, a
1
, a
2
}
, T
1
=
{
t
1
, t
2
}
T1
T2
A1
rental
starter
A2
rental
ender
CA1
renter
rental start
rental end
Figure 7:
h
A
1
, T
1
i
.
h
A
1
, T
1
i
is a sub-OCD.
γ(T
1
) =
{
a
0
, a
2
, a
3
}
⊆ A
1
A
1
= {a
0
, a
1
, a
2
} ⊆ γ(T
1
)
SSEO 2015 - Special Session on Enterprise Ontology
474
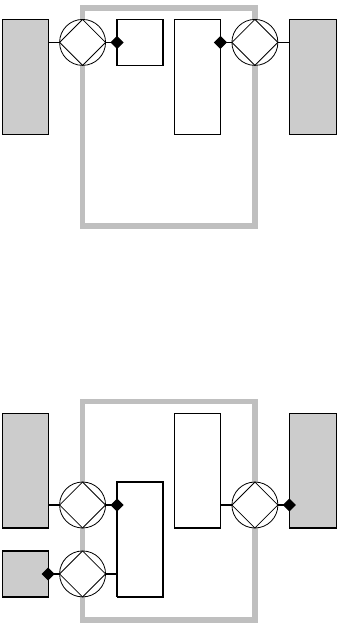
• A
2
=
{
a
0
, a
1
, a
3
, a
4
}
, T
2
=
{
t
1
, t
3
}
A3
car
issuer
T1
A1
rental
starter
T3
CA1
renter
CA2
driver
rental start car pick up
Figure 8:
h
A
2
, T
2
i
.
h
A
2
, T
2
i
is a sub-OCD.
γ(T
2
) =
{
a
0
, a
1
, a
3
, a
4
}
⊆ A
2
A
2
= {a
0
, a
1
, a
3
, a
4
} ⊆ γ(T
2
)
• A
3
=
{
a
0
, a
2
, a
3
, a
4
, a
5
}
, T
3
=
{
t
2
, t
4
, t
5
}
A3
car
issuer
T2
A2
rental
ender
T5
T4
CA1
renter
CA2
driver
CA3
payer
rental end
rental payment
car drop off
Figure 9:
h
A
3
, T
3
i
.
h
A
3
, T
3
i
is a sub-OCD.
γ(T
3
) =
{
a
0
, a
2
, a
3
, a
4
, a
5
}
⊆ A
3
A
3
= {a
0
, a
2
, a
3
, a
4
, a
5
} ⊆ γ(T
3
)
5 MERGE OPERATION ON
SUB-OCD
In this section, we consider an operation and show
that a sub-OCD is closed under the operation. An
abstract notation of a merge operation is defined as
follows, using the analogy of union in set theory. It is
because the same actor roles are merged into one actor
role, and the same transaction kinds into one transac-
tion kind.
Definition 9 (Syntactical Merge Operation). Given
a OCD
h
A
◦
, T
◦
i
and its two sub-OCDs
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
, a syntactical merge operation
∇ :
2
ActorRole
× 2
Transaction
×
2
ActorRole
× 2
Transaction
→
2
ActorRole
× 2
Transaction
is defined as follows.
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
=
h
A
X
∪ A
Y
, T
X
∪ T
Y
i
Based on the definition above, there exists two im-
portant properties for the merge operation such that
(1) if we apply the merge operation for two sub-OCDs
from a family of sub-OCDs results in a sub-OCD
from the same family, and that (2) the merge opera-
tion is commutative and associative on the family of
sub-OCDs.
Theorem 1 (Closed Merge Operation). A family of
sub-OCDs D
?
⊆ 2
A
◦
× 2
T
◦
is closed under the merge
operation ∇, i.e. for ∀
h
A
X
, T
X
i
∈ D
?
, ∀
h
A
Y
, T
Y
i
∈ D
?
,
(
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
) ∈ D
?
Theorem 2 (Commutative and Associative Merge
Operation). The merge operation ∇ is commuta-
tive and associative on a family of sub-OCDs D
?
⊆
2
A
◦
× 2
T
◦
, i.e. for ∀
h
A
X
, T
X
i
∈ D
?
, ∀
h
A
Y
, T
Y
i
∈
D
?
, ∀
h
A
Z
, T
Z
i
∈ D
?
,
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
=
h
A
Y
, T
Y
i
∇
h
A
X
, T
X
i
and
(
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
)∇
h
A
Z
, T
Z
i
=
h
A
X
, T
X
i
∇(
h
A
Y
, T
Y
i
∇
h
A
Z
, T
Z
i
)
hold.
Proposition 2 (Units of Algebra).
h
/
0,
/
0
i
and
h
A
◦
, T
◦
i
satisfy the five conditions of OCD.
h
/
0,
/
0
i
is the identity
element, and
h
A
◦
, T
◦
i
is the absorbing element (zero
element). Given an OCD
h
A
◦
, T
◦
i
, for any sub-OCD
h
A, T
i
among a family of sub-OCDs D
?
,
h
/
0,
/
0
i
∇
h
A, T
i
=
h
A, T
i
∇
h
/
0,
/
0
i
=
h
/
0,
/
0
i
and
h
A
◦
, T
◦
i
∇
h
A, T
i
=
h
A, T
i
∇
h
A
◦
, T
◦
i
=
h
A
◦
, T
◦
i
hold.
Although the proof of Proposition 2 is obtained
straightforward by the definition of ∇ (see Defini-
tion 9), it is important to note that
{h
/
0,
/
0
i}
∪ D
?
∪
{h
A
◦
, T
◦
i}
is an algebraic structure (with the identity
element and absorbing element) that is closed under
∇, based on Theorem 1, Theorem 2, and Proposition
2.
6 DISCUSSION
Finally, the authors will present the meaning of merge
operation using the example of EU-Rent. According
to Example 3,
h
A
1
, T
1
i
,
h
A
2
, T
2
i
and
h
A
3
, T
3
i
belong to
the family of sub-OCDs D
?
.
Does ‘Merging DEMO Models’ Satisfy the Associative Law? - Validation of Partial Models and Merge Operation
475

T1
T2
A1
rental
starter
A2
rental
ender
CA1
renter
rental start
rental end
∇
A3
car
issuer
T1
A1
rental
starter
T3
CA1
renter
CA2
driver
rental start car pick up
=
T1
T2
A1
rental
starter
A2
rental
ender
CA1
renter
rental start
rental end
A3
car
issuer
T3
CA2
driver
rental start car pick up
Figure 10:
h
A
1
, T
1
i
∇
h
A
2
, T
2
i
=
h
A
4
, T
4
i
.
T1
T2
A1
rental
starter
A2
rental
ender
CA1
renter
rental start
rental end
∇
A3
car
issuer
T1
A1
rental
starter
T3
CA1
renter
CA2
driver
rental start car pick up
=
T1
T2
A1
rental
starter
A2
rental
ender
CA1
renter
rental start
rental end
A3
car
issuer
T3
CA2
driver
rental start car pick up
=
A3
car
issuer
T1
A1
rental
starter
T3
CA1
renter
CA2
driver
rental start car pick up
∇
T1
T2
A1
rental
starter
A2
rental
ender
CA1
renter
rental start
rental end
Figure 11:
h
A
1
, T
1
i
∇
h
A
2
, T
2
i
=
h
A
4
, T
4
i
=
h
A
2
, T
2
i
∇
h
A
1
, T
1
i
.
Let us consider to merge
h
A
1
, T
1
i
and
h
A
2
, T
2
i
to
obtain the merged model
h
A
4
, T
4
i
.
h
A
1
, T
1
i
∇
h
A
2
, T
2
i
=
h
A
1
∪ A
2
, T
1
∪ T
2
i
=
h
{a
0
, a
1
, a
2
} ∪ {a
0
, a
1
, a
3
, a
4
}, {t
1
, t
2
} ∪ {t
1
, t
3
}
i
=
h
{a
0
, a
1
, a
2
, a
3
, a
4
}, {t
1
, t
2
, t
3
}
i
=
h
A
4
, T
4
i
Theorem 1 is illustrated as
h
A
4
, T
4
i
=
h
{a
0
, a
1
, a
2
, a
3
, a
4
}, {t
1
, t
2
, t
3
}
i
∈ D
?
. The corre-
sponding graphical representation in Figure 10 shows
that the obtained
h
A
4
, T
4
i
surely looks being an OCD.
Theorem 2 is illustrated as follows. For the com-
mutativity (shown in Figure 11),
h
A
1
, T
1
i
∇
h
A
2
, T
2
i
=
h
{a
0
, a
1
, a
2
} ∪ {a
0
, a
1
, a
3
, a
4
}, {t
1
, t
2
} ∪ {t
1
, t
3
}
i
=
h
{a
0
, a
1
, a
2
, a
3
, a
4
}, {t
1
, t
2
, t
3
}
i
and
h
A
2
, T
2
i
∇
h
A
1
, T
1
i
=
h
{a
0
, a
1
, a
3
, a
4
} ∪ {a
0
, a
1
, a
2
}, {t
1
, t
3
} ∪ {t
1
, t
2
}
i
=
h
{a
0
, a
1
, a
2
, a
3
, a
4
}, {t
1
, t
2
, t
3
}
i
result in the goal.
h
A
1
, T
1
i
∇
h
A
2
, T
2
i
=
h
A
2
, T
2
i
∇
h
A
1
, T
1
i
For the associativity,
(
h
A
1
, T
1
i
∇
h
A
2
, T
2
i
)∇
h
A
3
, T
3
i
=
h
{a
0
, a
1
, a
2
, a
3
, a
4
}, {t
1
, t
2
, t
3
}
i
∇
h
{a
0
, a
2
, a
3
, a
4
, a
5
}, {t
2
, t
4
, t
5
}
i
=
h
{a
0
, a
1
, a
2
, a
3
, a
4
, a
5
}, {t
1
, t
2
, t
3
, t
4
, t
5
}
i
and
h
A
1
, T
1
i
∇(
h
A
2
, T
2
i
∇
h
A
3
, T
3
i
)
=
h
{a
0
, a
1
, a
2
}, {t
1
, t
2
}
i
∇
h
{a
0
, a
1
, a
2
, a
3
, a
4
, a
5
}, {t
1
, t
2
, t
3
, t
4
, t
5
}
i
=
h
{a
0
, a
1
, a
2
, a
3
, a
4
, a
5
}, {t
1
, t
2
, t
3
, t
4
, t
5
}
i
result in the goal.
(
h
A
1
, T
1
i
∇
h
A
2
, T
2
i
)∇
h
A
3
, T
3
i
=
h
A
1
, T
1
i
∇(
h
A
2
, T
2
i
∇
h
A
3
, T
3
i
)
7 CONCLUSION
This paper shows that if an OCD
h
A
◦
, T
◦
i
is given,
one can construct D by gathering some pairs of sub-
set of A
◦
and T
◦
, then construct D
?
by selecting the
pairs that satisfy Condition 4 and Condition 5 among
D. Now D
?
is a family of sub-OCDs. Indeed, a fam-
ily of sub-OCDs is endowed with a beneficial charac-
teristic which corresponds to the well-formedness in
UML Class Diagram studied in (Enjo et al., 2010). In
short, the most prominent finding of this study is that
if an OCD
h
A
◦
, T
◦
i
is given, a family of sub-OCDs
of
h
A
◦
, T
◦
i
is well-formed as it is and this fact is de-
rived just from the five conditions of OCD. No further
conditions and restrictions are needed in the case of
OCD
8
. Here, well-formedness means the closedness,
commutativeness, and associativeness.
Prior to explaining algebraic structure for a for-
malization of the DEMO CM, this paper prepared the
components in DEMO with the mathematical nota-
tion and defined a family of sub-OCDs. Based on
the formalization, the authors introduced the merge
operation on the CM and showed that the operation
conforms the closedness, commutativity, and associa-
tivity.
The questions raised in the opening section are
now answered.
Q1: What are the requirements for generating
an appropriate partial model from the overall
model?
– To ensure the five conditions of OCD are
enough. No further requirements are needed.
8
This is not always the case for other modeling lan-
guages. For the case of UML Class Diagram studied in
(Enjo et al., 2010), a family of well-formed Class Diagram
is a proper (or strict) subset of Class Diagram. It means
that some diagrams are well-formed but others are not well-
formed even if all of the diagrams satisfy all of the specifi-
cation of the notation as UML Class Diagram. Indeed, an
additional condition is required to be well-formed.
SSEO 2015 - Special Session on Enterprise Ontology
476
Q2: Is there any possibility to produce a broken
model (a model which does not follow the correct
syntax) when merging two partial models? i.e.
closedness
– No, merging two partial models always pro-
duces the correct model if the two satisfy the
five conditions. No need to worry about pro-
ducing a broken model which does not satisfy
the five conditions of OCD.
Q3: Does the order of merging matter?
i.e. commutativity: X+Y
?
= Y+X and associativity:
(X+Y)+Z
?
= X+(Y+Z)
– No, it does not matter. The equality is attained
for the both formula.
Therefore, it concludes that DEMO—at least OCD—
itself is consistent for the merge operation; no extra
conditions are needed for DEMO OCD to be well-
formed and to provide the closedness, commutativity,
and associativity.
The future work foresees an expansion of the
scope for formalization beyond the assumptions:
to include aggregate transaction kinds, information
links, and multiple initiator links for each transaction
kind. Concurrently with the expansion, it would be
worth introducing the concept of ‘the scope of inter-
est’ which is regarded as the system boundary on the
model.
REFERENCES
Baresi, L. and Pezz, M. (2001). On Formalizing UML with
High-Level Petri Nets. In Concurrent OOP and PN,
pages 276–304. Springer-Verlag Berlin Heidelberg.
Berardi, D., Calvanese, D., and Giacomo, G. D. (2001).
Reasoning on UML Class Diagrams using Descrip-
tion Logic Based Systems. In Proceedings of the KI-
2001 Workshop on Applications of Description Logics
(KIDLWS’01), pages 1–12.
Dietz, J. and Hoogervorst, J. (2014). The ψ-theory. In
TEEMs (Theories in Enterprise Engineering Memo-
randum).
Dietz, J. L. (2006). Enterprise Ontology. Springer Berlin
Heidelberg, Berlin, Heidelberg.
Dietz, J. L. (2012). DEMO-3 Way of Modelling Way of
Working (version 3.5, September 2012).
Dietz, J. L. (2013). DEMO-3 Models and Representations
(version 3.6c, March 2013).
Enjo, H., Tanabu, M., and Iijima, J. (2010). A Step Toward
Foundation of Class Diagram Algebra for Enterprise
Service Systems. In 6th International Conference on
Service Systems and Service Management, 2009. IC-
SSSM ’09, pages 412–417.
Klimek, R. and Szwed, P. (2010). Formal Analysis of Use
Case Diagrams. Computer Science, 11:115–131.
Liepins, R., Cerans, K., and Sprogis, A. (2012). Visu-
alizing and Editing Ontology Fragments with OWL-
GrEd. In Lohmann, S. and Pellegrini, T., editors, the
I-SEMANTICS 2012 Posters & Demonstrations Track,
pages 22–25, Graz, Austria.
Mancioppi, M., Danylevych, O., Karastoyanova, D., and
Leymann, F. (2012). Towards classification criteria
for process fragmentation techniques. Lecture Notes
in Business Information Processing, 99 LNBIP(PART
1):1–12.
Meng, S. and Aichernig, B. K. (2003). Towards a Coal-
gebraic Semantics of UML : Class Diagrams and Use
Cases. Technical report, UNU/IIST Report No. 272.
Moreira, A. M., Ringeissen, C., Déharbe, D., and Lima,
G. (2004). Manipulating algebraic specifications with
term-based and graph-based representations. Journal
of Logic and Algebraic Programming, 59(1-2):63–87.
Open Management Group (2013). Semantics of Business
Vocabulary and Business Rules (SBVR), V1.2 Annex
G - EU-Rent Example.
Op’t Land, M., Zwitzer, H., Ensink, P., and Lebel, Q.
(2009). Towards a fast enterprise ontology based
method for post merger integration. In Proceedings
of the 2009 ACM symposium on Applied Computing
- SAC ’09, number May 2004, page 245, New York,
New York, USA. ACM Press.
Perinforma, A. P. (2012). The Essence of Organization. Sa-
pio Enterprise Engineering.
Sengupta, S. and Bhattacharya, S. (2006). Formalization of
UML use case diagram - A Z notation based approach.
In 2006 International Conference on Computing and
Informatics, ICOCI ’06, pages 2–7.
Shroff, M. and France, R. B. (1997). Towards a formal-
ization of UML class structures in Z. Proceedings
Twenty-First Annual International Computer Software
and Applications Conference (COMPSAC’97), pages
646–651.
van Kervel, S. J. H. (2011). High Quality Technical Doc-
umentation for Large Industrial Plants Using an En-
terprise Engineering and Conceptual Modeling Based
Software Solution. Advances in Conceptual Model-
ing. Recent Developments and New Directions, pages
383–388.
Zhao, J. and Duan, Z. (2009). Verification of use case with
Petri nets in requirement analysis. Lecture Notes in
Computer Science (including subseries Lecture Notes
in Artificial Intelligence and Lecture Notes in Bioin-
formatics), 5593 LNCS(PART 2):29–42.
APPENDIX
Proof of Proposition 1: Partial Preservation of Sub-
Societies. Let
h
A
◦
, T
◦
i
be a given OCD. Then, the
first three conditions of OCD holds for every member
h
A, T
i
in a family of sub-Societies D obtained from
h
A
◦
, T
◦
i
.
Does ‘Merging DEMO Models’ Satisfy the Associative Law? - Validation of Partial Models and Merge Operation
477

• Condition 1: Unique Actor Role Name Axiom
Since
h
A
◦
, T
◦
i
is an OCD and thus a Society
by Definition 5,
h
A
◦
, T
◦
i
satisfies Condition 1.
Then, for any a
i
and a
j
in A
◦
, if f
ARname
(a
i
) =
f
ARname
(a
j
) then a
i
= a
j
. Next, let
h
A, T
i
be a
member of a family of sub-Societies D obtained
from
h
A
◦
, T
◦
i
. Now that A ⊆ A
◦
by Definition
8, for any a
i
and a
j
in A ⊆ A
◦
, if f
ARname
(a
i
) =
f
ARname
(a
j
) then a
i
= a
j
. It concludes that Con-
dition 1 holds for any
h
A, T
i
in D and thus holds
for a family of sub-Societies D.
• Condition 2: Unique Transaction Kind Name
Axiom
Since
h
A
◦
, T
◦
i
is an OCD and thus a Society by
Definition 5,
h
A
◦
, T
◦
i
satisfies Condition 2. Then,
for any t
i
and t
j
in T
◦
, if f
T name
(t
i
) = f
T name
(t
j
)
then t
i
= t
j
. Next, let
h
A, T
i
be a member of a
family of sub-Societies D obtained from
h
A
◦
, T
◦
i
.
Now that T ⊆ T
◦
by Definition 8, for any t
i
and t
j
in T ⊆ T
◦
, if f
T name
(t
i
) = f
T name
(t
j
) then t
i
= t
j
.
It concludes that Condition 1 holds for any
h
A, T
i
in D and thus holds for a family of sub-Societies
D.
• Condition 3: Numbering Axiom
Since
h
A
◦
, T
◦
i
is an OCD and thus a Society by
Definition 5,
h
A
◦
, T
◦
i
satisfies Condition 3. Then,
for any t in T
◦
, f
ARno
( f
Tex
(t)) = f
T no
(t) holds.
Next, let
h
A, T
i
be a member of a family of sub-
Societies D obtained from
h
A
◦
, T
◦
i
. Now that
T ⊆ T
◦
by Definition 8, for any t in T ⊆ T
◦
,
f
ARno
( f
Tex
(t)) = f
T no
(t) holds. It concludes that
Condition 3 holds for any
h
A, T
i
in D and thus
holds for a family of sub-Societies D.
Proof of Lemma 1: Another Expression of Con-
dition 4. Let
h
A
◦
, T
◦
i
be a given OCD, and
h
A, T
i
be an element of a family of sub-Societies
D obtained from
h
A
◦
, T
◦
i
. Then, ∀t ∈ T, ∀a ∈
ActorRole, (a ∈ f
Tin
(t) ∪ f
Tex
(t) ⇒ a ∈ A) if and
only if γ(T ) ⊆ A. This is obvious by Definition
6.
Proof of Lemma 2: Another Expression of Condition
5. Let
h
A
◦
, T
◦
i
be a given OCD, and
h
A, T
i
be an el-
ement of a family of sub-Societies D obtained from
h
A
◦
, T
◦
i
. Then, ∀a ∈ A, ∃t ∈ T, a ∈ f
Tin
(t) ∪ f
Tex
(t) if
and only if A ⊆ γ(T ). This is obvious by Definition
6.
Proof of Theorem 2: Commutative and Associa-
tive Merge Operation. Let
h
A
◦
, T
◦
i
be a given OCD.
Then, suppose
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
are elements of a
family of sub-OCDs D
?
that is obtained from
h
A
◦
, T
◦
i
via a family of sub-Societies D of
h
A
◦
, T
◦
i
. Closed in
a family of sub-Societies 2
A
◦
× 2
T
◦
Since
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
are sub-OCDs
of OCD
h
A
◦
, T
◦
i
,
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
are off
course in a family of sub-Societies D ⊆ 2
A
◦
× 2
T
◦
.
Thus, since A
X
⊆ A
◦
, T
X
⊆ T
◦
, A
Y
⊆ A
◦
, and
T
Y
⊆ T
◦
, A
X
∪ A
Y
⊆ A
◦
and T
X
∪ T
Y
⊆ T
◦
.
Since
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
=
h
A
X
∪ A
Y
, T
X
∪ T
Y
i
by Definition 9,
h
A
X
∪ A
Y
, T
X
∪ T
Y
i
⊆
{
(A, T )
|
A ⊆ A
◦
, T ⊆ T
◦
}
holds. It concludes
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
∈ 2
A
◦
× 2
T
◦
.
• Condition 4: Closed OCD Axiom for Actor Role
Since
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
are sub-OCDs of
OCD
h
A
◦
, T
◦
i
,
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
satisfy Con-
dition 4 by Definition 8. With Lemma 1,
γ(T
X
) ⊆ A
X
and γ (T
Y
) ⊆ A
Y
hold for
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
respectively. Thus, γ (T
X
) ∪ γ (T
Y
) ⊆
A
X
∪ A
Y
. Combining this and γ (T
X
∪ T
Y
) =
γ(T
X
)∪γ (T
Y
), γ(T
X
∪ T
Y
) ⊆ A
X
∪A
Y
holds. Since
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
=
h
A
X
∪ A
Y
, T
X
∪ T
Y
i
by Defi-
nition 9, Condition 4 is satisfied by Lemma 1 for
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
.
• Condition 5: Actor Role Participation Axiom
Since
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
are sub-OCDs of
OCD
h
A
◦
, T
◦
i
,
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
satisfy Con-
dition 5 by Definition 8. With Lemma 2,
A
X
⊆ γ (T
X
) and A
Y
⊆ γ (T
Y
) hold for
h
A
X
, T
X
i
and
h
A
Y
, T
Y
i
respectively. Thus, A
X
∪ A
Y
⊆
γ(T
X
) ∪ γ (T
Y
). Combining this and γ (T
X
∪ T
Y
) =
γ(T
X
)∪γ (T
Y
), A
X
∪A
Y
⊆ γ (T
X
∪ T
Y
) holds. Since
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
=
h
A
X
∪ A
Y
, T
X
∪ T
Y
i
by Defi-
nition 9, Condition 5 is satisfied by Lemma 2 for
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
.
Proof of Theorem 2: Commutative and Associa-
tive Merge Operation. Let
h
A
◦
, T
◦
i
be a given OCD.
Then, suppose
h
A
X
, T
X
i
,
h
A
Y
, T
Y
i
, and
h
A
Z
, T
Z
i
are
elements of a family of sub-OCDs D
?
that is ob-
tained from
h
A
◦
, T
◦
i
via a family of sub-Societies D
of
h
A
◦
, T
◦
i
. Now the commutativity and associativity
are confirmed as below.
Commutativity:
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
=
h
A
X
∪ A
Y
, T
X
∪ T
Y
i
=
h
A
Y
∪ A
X
, T
Y
∪ T
X
i
∵ commutative law of ∪
=
h
A
Y
, T
Y
i
∇
h
A
X
, T
X
i
Associativity:
(
h
A
X
, T
X
i
∇
h
A
Y
, T
Y
i
)∇
h
A
Z
, T
Z
i
=
h
A
X
∪ A
Y
, T
X
∪ T
Y
,
i
∇
h
A
Z
, T
Z
i
=
h
(A
X
∪ A
Y
) ∪ A
Z
, (T
X
∪ T
Y
) ∪ T
Z
i
=
h
A
X
∪ (A
Y
∪ A
Z
), T
X
∪ (T
Y
∪ T
Z
)
i
∵ associative law of ∪
=
h
A
X
, T
X
i
∇
h
A
Y
∪ A
Z
, T
Y
∪ T
Z
,
i
=
h
A
X
, T
X
i
∇(
h
A
Y
, T
Y
i
∇
h
A
Z
, T
Z
i
)
SSEO 2015 - Special Session on Enterprise Ontology
478
