A Heuristic Solution for Noisy Image Segmentation using Particle Swarm

Optimization and Fuzzy Clustering

Saeed Mirghasemi, Ramesh Rayudu and Mengjie Zhang

School of Engineering and Computer Science, Victoria University of Wellington, Wellington, New Zealand

Keywords:

Noisy Image Segmentation, Fuzzy C-Means, Particle Swarm Optimization, Impulse Noise.

Abstract:

Introducing methods that can work out the problem of noisy image segmentation is necessary for real-world

vision problems. This paper proposes a new computational algorithm for segmentation of gray images contam-

inated with impulse noise. We have used Fuzzy C-Means (FCM) in fusion with Particle Swarm Optimization

(PSO) to deﬁne a new similarity metric based on combining different intensity-based neighborhood features.

PSO as a computational search algorithm, looks for an optimum similarity metric, and FCM as a clustering

technique, helps to verify the similarity metric goodness. The proposed method has no parameters to tune, and

works adaptively to eliminate impulsive noise. We have tested our algorithm on different synthetic and real

images, and provided quantitative evaluation to measure effectiveness. The results show that, the method has

promising performance in comparison with other existing methods in cases where images have been corrupted

with a high density noise.

1 INTRODUCTION

The concept of partitioning an image into homo-

geneous regions, usually referred to as image seg-

mentation, is an important mid-level image analy-

sis technique for many high-level afterwards applica-

tions such as object detection (Zhuang et al., 2012;

Ant

uNez et al., 2013), image recognition (Ferrari

et al., 2006; Kang et al., 2011), image retrieval (Mei

and Lang, 2014), image compression (Zhang et al.,

2014), and video control/surveillance (Mahalingam

and Mahalakshmi, 2010; Zhang et al., 2009). Since

its emersion in mid 20th century, it has been revolu-

tionized a lot, not only to be applied to more practi-

cal problems, but also to cope with the unstoppable

trend of demand for more accurate detection, classi-

ﬁcation, and recognition in a variety of applications.

A small but quite practicable section of image seg-

mentation is devoted to noisy image segmentation in

which fuzzy clustering usually performs as a powerful

tool (Cai et al., 2007). The common fuzzy clustering

algorithm for this matter is Fuzzy C-Means (FCM)

(Hathaway et al., 2000) which due to simplicity and

applicability is one of the most used clustering algo-

rithms. It is also known for better performance in case

of poor contrast, overlapping regions, noise and in-

tensity inhomogeneities (Benaichouche et al., 2013).

The fuzzy membership of FCM allows each datapoint

to belong to every existing cluster with different de-

grees of membership. This is especially of interest in

noisy data clustering where it has been widely used to

cluster noisy contaminated data.

Lots of the so far proposed FCM-based algorithms

for noisy image segmentation are parameter depen-

dent (Ahmed et al., 1999; Szilagyi et al., 2003; Chen

and Zhang, 2004; Cai et al., 2007). Usually, these

parameters make a trade-off between preserving the

details in an image and eliminating the noise which

makes the applicability of these methods limited to

noisy images in which the amount of noise is known.

This means that the best segmentation results are only

obtained when a prior knowledge of the noise volume

is available. Another issue is that they usually fail to

perform well when the image is presented with heavy

impulse noise as a common type of noise mainly be-

cause impulse noises are not easy to deal with.

This paper introduces a heuristic fuzzy algorithm

for noisy image segmentation with no parameters

to tune in advance according to the noise volume.

The utilized features have been speciﬁcally chosen to

compensate for impulse noise, and the algorithm has

been designed to confront heavy noise. In this way,

we incorporate spatial, texture, and fuzzy member-

ship values to achieve better results.

The rest of this paper is organized as follows. Sec-

tion 2 is devoted to the research background of this

study. Section 3 describes the proposed method. Ex-

perimental results, datasets, and parameter settings

Mirghasemi, S., Rayudu, R. and Zhang, M..

A Heuristic Solution for Noisy Image Segmentation using Particle Swarm Optimization and Fuzzy Clustering.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 17-27

ISBN: 978-989-758-157-1

 2015 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

are presented in section 4, and section 5 is dedicated

to conclusions and future work.

2 BACKGROUND

This section starts with the introduction of the pri-

mary FCM and its variants. We then introduce PSO as

the heuristic algorithm we have utilized in this paper,

and then related work would be presented.

2.1 Fuzzy C-Means Related Algorithms

The Fuzzy C-Means (FCM) as a clustering algorithm

was ﬁrst introduced in (Dunn, 1973), and then ex-

tended in (Hathaway et al., 2000). The aim in FCM is

to ﬁnd c partitions via minimizing the following ob-

jective function:

J =

∑

i=1

∑

j=1

) (1)

where X

X =

= {x

} is a dataset in which x

rep-

resents a p-dimensional array datapoint in R

, and N

is the number of datapoints (p is the number of fea-

tures attributed to each datapoint), C is the number

of clusters, u

i j

is the degree of membership of x

cluster j, which meets u

i j

∈ [0,1] and

∑

i=1

i j

= 1, m

is the degree of fuzziness, v

is the prototype of clus-

ter j, and d

) is the distance difference between

datapoint x

and cluster center v

. The two following

iterative formulas are necessary but not sufﬁcient for

J to be at its local extrema. u and v get updated using

these equations till termination threshold is satisﬁed:

∑

i=1





∑

i=1





(2)

k+1

∑

l=1





2/m−1

(3)

Although FCM itself fails at the segmentation of

noisy images, utilizing the basic concept a number

of algorithms have been created to cover this failure

(Ahmed et al., 1999; Chen and Zhang, 2004; Szilagyi

et al., 2003; Cai et al., 2007; Krinidis and Chatzis,

2010). A common approach in this manner (Ahmed

et al., 1999) known as FCM S was introduced in

which FCM objective function is modiﬁed to deal

with intensity inhomogeneities posing in segmen-

tation of magnetic resonance images. The new

objective function is as follows:

J =

∑

i=1

∑

j=1

) +

∑

i=1

∑

j=1

∑

r∈N

)

(4)

where N

is the set of neighbors within the neighbor-

ing window around x

, N

is its cardinality, and x

rep-

resents the neighbor of x

. How the neighbors are af-

fecting the objective function is controlled by α. The

new updating formulas for u and v are obtained ac-

cording to Lagrange multipliers taking partial deriva-

tives of the new objective function. The new objec-

tive function allows the neighboring pixels to affect

the labeling procedure of a pixel. Then two modiﬁ-

cations of FCM S algorithm were proposed in (Chen

and Zhang, 2004) mainly trying to reduce the com-

putation of FCM S. These two algorithms known as

FCM S1 and FCM S2 use a pre-calculated mean and

median-ﬁltered image of the noisy image as a sub-

stitution for neighbor pixel labeling in each iteration

which results in a faster algorithm. The modiﬁed ob-

jective function is:

J =

∑

i=1

∑

j=1

) + α

∑

j=1

∑

r∈N

) (5)

where x

is the mean or median average of the

neighboring pixels around x

For even a faster performance, EnFCM was pro-

posed (Szilagyi et al., 2003). Here again, a linearly-

weighted local ﬁlter is applied to image in advance

according to:

1 + α



∑

r∈N



(6)

in which ξ

is the gray level value of the pixel i, and

α plays the same role as before. Then the clustering

procedure is performed on the gray-level histogram

obtained from the ﬁltered image. As there are only

256 gray levels in an image, and having in mind that

the number of pixels in an image are generally much

larger than 256, this algorithm is quite fast, and also

has better performance in noisy image segmentation

compared to FCM S. The new objective function is

introduced as:

J =

∑

i=1

∑

j=1

(ξ

) (7)

where Q denotes the number of gray levels, and ξ

the number of pixels having a gray value equal to i.

The so far mentioned algorithms, although having

great achievements dealing with noise, they all suf-

fer from a common problem which is the parameter

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

α. This parameter keeps a trade-off between the vol-

ume of noise and the details of an image. In other

words, it should be large enough to compensate for

noise and should be small enough to preserve details

of an image like edges. That is why the performance

of these algorithms is α-dependent which is a disad-

vantage when dealing with generic image segmenta-

tion. To make up for this, FGFCM was proposed in

(Cai et al., 2007) incorporating local spatial and gray

information. A new ﬁltering factor, S

i j

is proposed

which acts as a local similarity measure:

i j



−max(|p

−p

|,|q

−q

|/λ

)−||x

−x

/λ

, i 6= j

0 i = j

(8)

∑

j∈N

k x

− x

(9)

where i stands for the pixels in the center of the sliding

window, and j is one of the neighboring pixels falling

in the neighborhood window, and (p

) is the coor-

dinates of the pixel k in the neighboring window. λ

and λ

are parameters with functioning similar to α.

Like EnFCM, FGFCM performs clustering on the ba-

sis of histogram information obtained from the pro-

posed ﬁltering factor. Although FGFCM acts less

parameter-independent introducing λ

and λ

, again

its performance is inﬂuenced by the variation of λ

(Krinidis and Chatzis, 2010).

Regardless of the fact that all these methods per-

form reasonably well on noisy image segmentation,

they have parameters that need to be tuned according

to the volume and type of noise. Although λ

could

be ﬁxed in 3 according to (Cai et al., 2007), α and λ

have to be adjusted empirically. They have to be large

to make up for the noise, and have to be small to keep

the details of an image. This makes the applicabil-

ity of them limited to images with prior information

about the noise and its volume. Therefore, the need

for parameter-free algorithms which can adaptively

be used for noisy image segmentation is essential. In

addition, the existing methods fail to produce accurate

segmentation results when the noise is heavy, which

is another motivation for the proposed method in this

paper.

2.2 Particle Swarm Optimization

Particle Swarm Optimization is a computational op-

timization algorithm introduced in (Eberhart and

Kennedy, 1995; Kennedy and Eberhart, 1995). Due

to efﬁciency, robustness, and simplicity (Engelbrecht,

2007) the technique has been modiﬁed many times,

for general and speciﬁc applications. The search al-

gorithm is motivated by the social behaviors of or-

ganisms. Particularly, choreography of birds ﬂock

led to the design of PSO. The algorithm is initial-

ized with a swarm of potential solutions in a mul-

tidimensional space. Each solution, also known as

particle, has the ability to move. Therefore, parti-

cle i has two parameters as x and v which specify

its location and speed in the search space, respec-

tively. During the movement, each particle updates

its position and velocity according to its own expe-

rience, and that of its neighbors. i is in interactive

communication with neighboring particles in order

to ﬁnd the best position (ﬁnal solution). The best

so-far position of each particle is called pbest, and

the best so-far position in the whole swarm is called

gbest. What really determines the goodness of pbest,

gbest, and basically all particles is a ﬁtness function

which is an essential part of PSO algorithm. The ﬁt-

ness function speciﬁes the nature of the optimization

problem, and is designed according to the applica-

tion. Brieﬂy, assuming a D-dimensional search space

the ith particle is represented by X

= (

(

)

and V

= (

(

)

) as D-dimensional arrays

for the positions and velocities. x

x and v

v are updated

using these two equations:

k+1

= w ×v

(pbest

−x

)+c

(gbest

−x

)

(10)

k+1

= x

+ v

k+1

(11)

where d = 1,2,...,D, i = 1,2,...,N, are the sizes of di-

mension and swarm, c

and c

are positive constants,

and r

are random numbers, uniformly distributed

in the interval [0,1], k = 1, 2,..., denotes the iteration

number, pbest

and gbest

represent pbest and gbest

in the dth dimension, and w is inertia weight which

controls the inﬂuence of previous velocities on the

new velocity. Larger inertia weights indicate larger

exploration through the search space while smaller

values of the inertia weight restrict the search on a

smaller space (Engelbrecht, 2007). Typically, PSO

starts with a larger w, and the decreases gradually over

the iterations. We have adopted the following equa-

tion for w to simulate its descending property:

w = (w

initial

− w

f inal

) ×

max

− k)

max

+ w

f inal

(12)

where w

initial

, is the preliminary value of w, w

f inal

the ﬁnal value of w, k is the iteration number, and k

max

is the maximum number of iterations.

A Heuristic Solution for Noisy Image Segmentation using Particle Swarm Optimization and Fuzzy Clustering

2.3 Related Work

A couple of research works have been proposed in an

attempt to combine heuristic algorithms particularly

PSO with FCM. The common approach (Zhang et al.,

2012; Benaichouche et al., 2013; Tran et al., 2014)

is that potential solutions (particles) are possible val-

ues for cluster centers within the intensity diversity of

pixels. They take the objective function of a FCM-

based clustering method as the ﬁtness function, and

then try to ﬁnd the optimum positions of the clus-

ter centers that minimize the objective function the

most. This will omit the updating formula for cluster

centers, but again, they need the fuzzy membership

updating formula to obtain the value of membership.

That is why these approaches do not really create a

new algorithm, rather they just try to optimize an ex-

isting one. Knowing that, the FCM-based clustering

methods are already computationally optimized, these

approaches fall effective in special cases that the ob-

jective function of an already existing FCM-based al-

gorithm is not simple enough to be completely opti-

mized by its iterative procedure itself. Since the im-

provement is not signiﬁcant often for such an opti-

mization case, the better performance is achieved by

including other criteria to the existing algorithm (Tran

et al., 2014; Benaichouche et al., 2013).

Another trend in the literature is investigating the

effect of Gaussian noise in noisy image segmenta-

tion. This paper, unlike the common trend, is focused

on impulse noises as another common type of noise

in image processing. Impulse or fat-tail distributed

noise, which sometimes is referred to as salt and pep-

per noise, can be produced by malfunctioning pixels

in camera sensors, faulty memory locations in hard-

ware, analog-to-digital converter errors or bit errors in

a transmission (Bovik, 2005). This means, images are

usually damaged by impulsive noises during acqui-

sition or transmission. It appears as sparsely occur-

ring white and black pixels. Since the corrupted pixel

by impulsive noise contains no information about the

present image, impulse noisy image segmentation is a

challenging issue.

The proposed approach in this paper, unlike the

existing approaches, uses PSO to deﬁne a new simi-

larity criterion for FCM in which segregation between

two datapoints (pixels here) happens by combining

different features extracted from a neighboring win-

dow around each pixel. For this, the new measure-

ment criterion not only utilizes gray and spatial in-

formation, but also uses the fuzzy membership value

to achieve a better performance. Our method intro-

duces a new optimization process in which FCM clus-

tering performance on noisy image segmentation gets

improved by modifying the classic Euclidean metric.

This is different from the common trend that uses

PSO for a better initialization of FCM.

3 THE PROPOSED METHOD

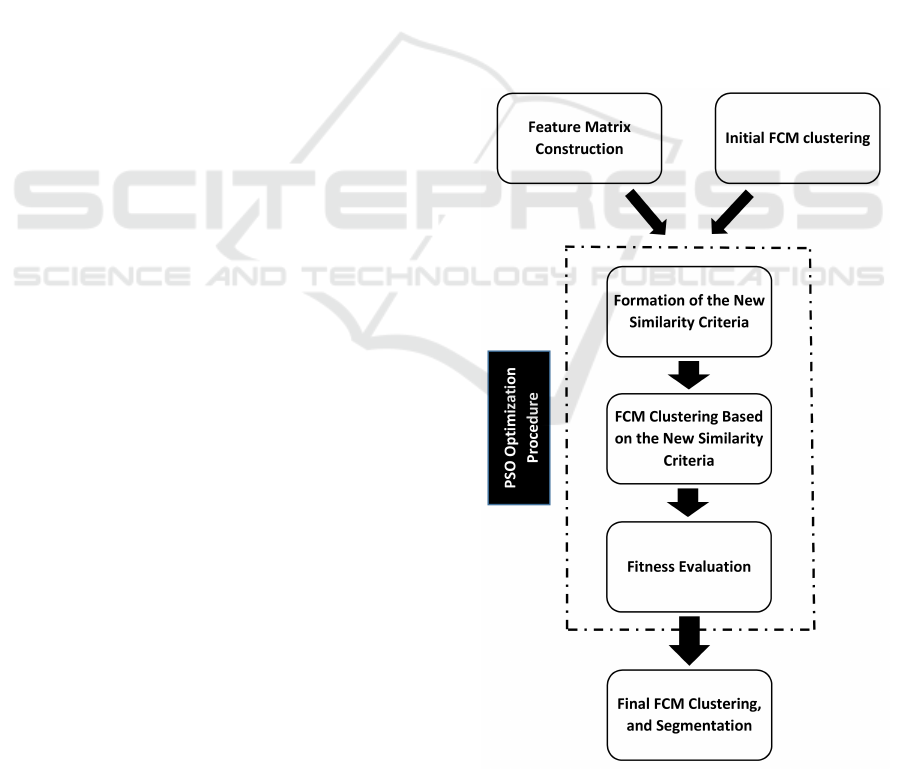
Fig. 1 shows a block diagram of the proposed

method. This ﬁgure shows three main steps in

the algorithm: initialization and pre-processing,

PSO search procedure, and ﬁnal clustering and

segmentation. The general idea is to use PSO to form

a new similarity criterion based on simple texture

properties of a local neighboring window. During the

iterations of the PSO search procedure, FCM will be

used to obtain the parameters related to similarity

measure, and to cluster the noisy data based on

the new similarity criterion. Simply saying, PSO

along with FCM, creates a search space in which the

parameters related to the new similarity measure will

be gradually and automatically optimized.

Figure 1: Block diagram of the proposed method.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

3.1 Pre-processing and Initialization

The ﬁrst step of the proposed algorithm deals with

some initializations and feature construction. The ini-

tialization is carried out via a standard FCM accord-

ing to (2) and (3). This initial clustering provides the

initial cluster centers, V , and the initial membership

values, U, for the PSO procedure in which the new

similarity measurement is formed. This preprocess-

ing not only leads to better segmentation results at the

end, but also builds a deterministic algorithm with sta-

ble outputs.

Feature construction is done in advance for more

simple and efﬁcient implementation. Simple texture

information of a local window around each pixel will

be used to construct the feature matrix. The texture in-

formation is captured by four statistical-based ﬁlters

which apply to the intensity values of the pixels in-

side the neighboring window. These sliding-window

ﬁlters employ median, variance, standard deviation,

and Wiener ﬁltering.

The Wiener ﬁlter (Wiener, 1964) low-pass ﬁlters

a grayscale image that has been degraded by ad-

ditive noise. The ﬁlter uses a pixel-wise adaptive

Wiener method based on statistics estimated from a

local neighborhood of each pixel. The Wiener ﬁlter-

ing is a general way of ﬁnding the best reconstruc-

tion of a noisy signal. More specially, it can gener-

ally be applied whenever you have a basis-in-function

space that concentrates “mostly signal” in some com-

ponents relative to “mostly noise” in others. It could

be applied on spatial or wavelet function basis. In spa-

tial (pixel) basis (as utilized in this paper), the Wiener

ﬁlter is usually applied to the difference between an

image and its smoothed version. It gives the optimal

way of tapering off the noisy components, so as to

give the best (L

norm) reconstruction of the origi-

nal signal. Assuming an observation (noisy image)

), which is composed of the original image (S

) and

noise (N

), we have the measured components as:

= S

+ N

(13)

The ﬁlter looks for a signal estimator that scales

the individual components of what is measured as:

= C

(14)

and ﬁnds the signal estimator, Φ

, such that it min-

imizes h|

S − S|

i. Knowing that we are working on

some orthogonal basis, the L

norm is just the sum of

squares of the components of what is measured, we

extend the latter, differentiate with respect to Φ

, and

set it to zero to obtain:

i + hN

(15)

where hS

i and hN

i are estimations of signal and

noise power in each component. Using the estimator

introduced in (Lim, 1990), Wiener estimates the local

mean (ρ), and variance (σ

) around each pixel:

ρ =

∑

∈η

a(n

)

∑

∈η

) − ρ

(16)

where η is the N ×M local neighborhood of each pixel

in the image, and n

and n

are the coordinates of

pixel a. Then, a pixel-wise Wiener ﬁlter using these

estimates is created:

b(n

) = ρ +

− v

(a(n

) − ρ) (17)

where v

is the noise variance related to the average

of all the local estimated variances.

Although some of the ﬁlters for constructing the

feature matrix have been individually used for FCM-

based image segmentation (Chen and Zhang, 2004),

this is the ﬁrst time that their combination is used

for noisy image segmentation. To be able to com-

bine noise degradation properties of each ﬁlter on an

image, we use them all to build a new similarity cri-

terion. This not only allows us to beneﬁt from the

properties of each ﬁlter, but also gives our approach

the ability to adaptively come up with a unique solu-

tion for each image.

3.2 A New Similarity Measure

The main contribution of this paper is that it incorpo-

rates simple statistical features of a neighboring win-

dow around each pixel into the distance calculation

metric of the classical FCM using PSO. Motivated by

the texture detection algorithm in (Tian et al., 2013),

we modify d

) in (1) as below:

) =k x

− v

k (1 −

∑

p=1

i j(p)

) (18)

where k x

− v

k is the Euclidean distance between

the gray (intensity) information of each pixel and jth

cluster center, p is the number of features, and µ

are

the coefﬁcients to be obtained subjected to:

0 < µ

< 1 (19a)

∑

p=1

i j(p)

≤ 1 (19b)

A Heuristic Solution for Noisy Image Segmentation using Particle Swarm Optimization and Fuzzy Clustering

i j

is a fusion of one-at-a-time (one out of four) fea-

ture attributed to each pixel, and some other informa-

tion from the rest of pixels falling inside the neighbor-

ing window as:

i j

∑

n=1

× ( f

− f

) × (e

−|x

−v

)

∑

n=1

( f

− f

) × (e

−|x

−v

)

(20)

where n is the index for the pixels within the

neighboring window for the similarity metric (N

is the cardinality of neighboring pixels), u is the

fuzzy membership value, f is the considering feature

from the previously-built feature matrix, f

is the

corresponding feature value of the pixel x

at the

center of the neighboring window for the similarity

metric, x is the intensity values, and v

is the cluster

center for cluster j. µ coefﬁcients are determined

and optimized gradually during the PSO procedure to

produce a proper similarity measure that can mitigate

the inﬂuence of noise to the greatest extend.

Equation (18) tries to reduce the distance between

a pixel and a cluster center with respect to the

information obtained from the neighboring window

around the pixel. This is not limited to only one

feature though, as (18) indicates. This is due to the

requirement that one feature alone may not be able

to attenuate the effect of noise. Having different

features included in the new similarity measure,

the search procedure provided by PSO enables this

reduction to take the best out of each feature in an

optimizing manner.

In addition, we have no parameters which need

tuning according to the noise volume. In our method,

all the related parameters (except for the neighboring

window sizes) in the similarity criterion get tuned

automatically during the iterations of PSO procedure

according to the noise properties of the test image.

3.3 PSO Representation

Apart from general motivations to utilize PSO for op-

timization problems (mentioned in sub-section 2.2),

simplicity of representing our optimizing problem in

the form of a PSO-based process is another motiva-

tion. The particle representation of PSO suits well

our objectives toward obtaining the optimum weights

for the new similarity measure. Also, the encoding

and decoding procedure is quite straightforward in

our problem. Overall, PSO is utilizes to adaptively

tune all the parameters associated with the new sim-

ilarity measure speciﬁcally for each image, based on

the volume of noise and feature properties.

The previously constructed feature matrix, initial

fuzzy membership values and cluster centers are used

as inputs for the PSO optimization procedure. As (18)

and (20) indicate, the new similarity criterion is de-

signed using four features. Associated with each fea-

ture is a µ coefﬁcient. PSO is applied to ﬁnd the best

contribution of each feature by determining µ values.

Therefore, each particle, p

, contains potential values

for µ coefﬁcients in form of p

= (

(

(µ

,µ

)

) that

demonstrates a 4-D search space.

The search space, as (19a) suggests, is deﬁned as

the smooth interval (0,1) for each dimension, and is

restricted continuously according to (19b). During

the PSO search, for each proposed combination of

µ values, FCM clustering is performed using (2) and

(3), and then the PSO ﬁtness function is calculated

to evaluate the combination. The ﬁtness function (1)

in which d

) has been substituted by the new

similarity measure as in (18). The best p

is the parti-

cle that minimizes the ﬁtness function the most. The

ﬁtness function, which basically drives the search al-

gorithm, conveys two important values to the next it-

eration:

1. The best solution that results in the minimum

value of the ﬁtness function.

2. The cluster centers that correspond to that solu-

tion.

When the PSO search ﬁnishes, the ﬁnal combina-

tion of µ values is used for one ﬁnal clustering. Then,

the pixels will be labeled according to their biggest

membership value to create a segmented image.

One disadvantage of FCM is that it easily gets

trapped in local minima and fails to achieve the

optimum results. To overcome this, the initial four

dimensional array is set to very small positive values.

The inertia factor, w, as a factor to control particle

velocity during the search, has bigger values in the

beginning and smaller values towards the end of the

search. As mentioned in (Mirghasemi et al., 2012),

selecting values between [1,0.5] with the mentioned

updating formula leads to maximum velocity com-

patibility.

3.4 Summary of the Algorithm

Different steps of the proposed method could be sum-

marized as below:

1. Load the noisy image.

2. Build the feature matrix based on Wiener, median,

variance, and standard deviation measures of in-

tensity values in the neighboring window.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

3. Set the parameters for FCM clustering, including

the number of clusters.

4. Perform a standard FCM clustering to obtain ini-

tial values for U and V .

5. Initialize PSO with parameters for x, v, iteration

number, particle number, search space dimension

size, and inertia weight.

6. Propose an initial solution for µ

µ values.

7. Form the new similarity measure according to

(18).

8. Perform FCM clustering according to the new

similarity measurement.

9. Evaluate the ﬁtness function: calculate the objec-

tive function of FCM according to (1).

10. Form pbest and gbest according to the ﬁtness

value from step 9.

11. Update x and v according to (11) and (10).

12. Go back to step 6, unless it is the end of iterations.

13. Use the resultant optimized values of

(

(µ

,µ

)

) to do the ﬁnal similarity measure

calculation and FCM clustering.

14. Use the U matrix for image segmentation.

For a clearer depiction of the proposed algorithm,

the pseudocode is provided for the PSO search pro-

cedure in Algorithm 1. The parameters used in this

pseudocode are as follow: ps, X, V , Pbest, C, k, k

max

and w stand for population size, population’s position

matrix, population’s velocity matrix, the population’s

pbest matrix, matrix of population’s corresponding

cluster centres, iteration, iteration number, and iner-

tia weight, respectively.

3.5 Parameter Design

Both PSO and FCM algorithms have intrinsic param-

eters to set. Also, our method has measures for the

sizes of the local neighboring windows in both ﬁlter-

ing and new distance forming steps. This sub-section

provides details for all these parameters. As men-

tioned before, parameters related to the new similar-

ity criterion get tuned automatically, and do not need

prior setting. Based on experiments on two different

datasets of gray images, we came up with the parame-

ter adjustment shown in table 1. These parameters are

ﬁxed for every test image of each dataset, and none of

them need to be changed.

Algorithm 1: The PSO search steps.

1: Set the PSO parameters: x, v, k, k

max

, and w;  x is

initially [0.001,0.001,0.001,0.001]

2: Set particle one as gbest;

3: k = 0;

4: while k < k

max

5: Update w using(12);

6: for each particle i ∈ pi do

7: Form the new similarity metric according to

(18);

8: Perform FCM based on the new similarity met-

ric;

9: Evaluate f (x) according to (1);

10: end for

11: if k = 0 then

12: pbest = f (x);

13: gbest = min(Pbest);

14: c = C(gbest);

15: else

16: pbest = f (x) < pbest;

17: gbest = min(Pbest);

18: c = C(gbest);

19: Update V using (10) and restrict its growth;

20: Update X using (11) and restrict its growth;

21: k = k + 1;

22: end if

23: end while

24: Return gbest and c;

Table 1: Parameter Setting.

Parameter Value

Neighboring window for ﬁltering 5 ×5

Neighboring window for similarity criterion 5 × 5

Weighting exponent (m) 2

Termination threshold for FCM 0.001

Maximum number of iterations for FCM 100

Population size (ps) 20

Iteration number 50

The initial value of the ﬁrst solution 0.001

and c

in (10) 1

initial

and w

f inal

in (12) 1 and 0.5

4 EXPERIMENTAL RESULTS

AND ANALYSIS

In this section, we compare the robustness of our

method in heavy impulse noisy image segmentation

against four other methods. The ﬁrst one is the hard

clustering method K-means, and the other three are

fuzzy clustering methods named as FCM (Hathaway

et al., 2000), EnFCM (Szilagyi et al., 2003), and

FGFCM (Cai et al., 2007). EnFCM needs tuning for

α, and FGFCM needs tuning for λ

according to the

type and volume of noise. We take α = 1.8, λ

= 3,

and λ

= 6 by investigating the interval [0.5,6] for λ

A Heuristic Solution for Noisy Image Segmentation using Particle Swarm Optimization and Fuzzy Clustering

(a)

(b)

(c)

(d)

(e)

(f)

(g)

S1 S2 S3 S4 S5

Figure 2: The segmentation results of the proposed algorithm on some sample synthetic images. Rows (a) through (g) are

the noisy corrupted images, the ground truths, K-means, FCM, EnFCM, FGFCM, and our methods segmentation results,

respectively.

and the interval [0.2,8] for α which, according to our

experiments comes with the best performance of En-

FCM and FGFCM methods. To carry out quantita-

tive evaluation, we choose the Segmentation Accu-

racy (SA) introduced in (Ahmed et al., 1999):

SA =

∑

i=1

∩ S

∑

j=1

(21)

in which A

represents the number of segmented

pixels from the ith cluster and, S

is the number of

pixels belonging to the cluster i in the ground truth

image.

To evaluate our method from different perspec-

tives, we have utilized two different datasets. The

ﬁrst dataset is composed of synthetic images in which

the tested images are 256 × 256 pixels, except for the

image S1 in Fig. 2 which is 128 × 128 pixels. The

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

B1 B2 B3 B4 B5 B6

Figure 3: Segmentation results on Berkeley dataset. Rows (a) through (h) are the original images, the noisy corrupted images,

the ground truths, K-means, FCM, EnFCM, FGFCM, and our methods segmentation results, respectively.

second database is the Berkeley image segmentation

(Martin et al., 2001) which is composed of two

sets of images, namely BSDS300 and BSDS500.

These datasets are speciﬁcally created for image

segmentation and boundary detection, providing

ground truth for each image. Here, the images are

481 × 321 pixels.

Salt and pepper noise with heavy density of 30%

has been applied through all the testing procedure.

The time performance of our method varies depend-

ing on the image size and its complexity. FCM needs

various numbers of iterations for different images

to satisfy the speciﬁed termination threshold. On

average, for images of 256 × 256, on a Intel(R)

Core(TM) i7-4790 CPU @ 3.60GHz machine with

8GB of RAM, it takes 25 minutes for an image to get

processed.

Fig. 2 shows the segmentation results of some

sample synthetic noisy images where the proposed

method performs better in the segmentation of impor-

tant regions. The numbers of speciﬁed clusters are 2,

3, 3, 4, and 3 for S1 through S5 images, respectively.

Table 2 also shows the SA metric evaluation of the re-

A Heuristic Solution for Noisy Image Segmentation using Particle Swarm Optimization and Fuzzy Clustering

Table 3: Quantitative comparison for Fig. 3, according to the SA metric. Bold numbers indicate the best performance for

each image.

Algorithm B1 B2 B3 B4 B5 B6

K-means 85.3580 86.8103 19.6629 82.9203 70.9614 79.1877

FCM 85.0750 86.8103 19.6629 81.7412 70.9614 79.1877

EnFCM 67.2460 96.5247 58.7644 84.7205 65.4835 73.2668

FGFCM 79.4635 97.3976 66.8882 85.1418 67.2698 79.4748

Our method 96.3309 97.8440 98.8243 97.3401 95.2972 88.4101

Table 2: Quantitative comparison for Fig. 2, according to

the SA metric. Bold numbers indicate the best performance

for each image.

Algorithm S1 S2 S3 S4 S5

K-means 50.0585 84.8183 72.6301 82.7271 52.3180

FCM 85.0676 84.8183 72.6301 82.7271 78.6958

EnFCM 93.0931 95.3562 92.0351 75.4330 79.8469

FGFCM 97.3660 98.2033 99.1229 81.2957 89.4574

Our method 99.3301 98.9701 99.2961 98.2316 97.0128

sults in Fig. 2 on all ﬁve methods with bold numbers

representing the best performance for each test im-

age. This table shows that the proposed method per-

forms signiﬁcantly better than K-means, FCM, and

EnFCM. When it comes to FGFCM, our method still

performs visibly better on S1, S2, S4, and S5. To see

the segmentation difference of FGFCM and the pro-

posed method on image S3, one might need to have

a closer look to see the better performance of our

method. Qualitative evaluation also conﬁrms better

segmentation results obtained by our method. Only

FGFCM has close performance to our method spe-

cially on image S3.

Testing our method with the second database

comes with the segmentation results shown in Fig.

3. Here, six sample images named as B1-B6 are se-

lected. The number of clusters has been set to two

for the fuzzy clustering part in all of them except for

B4 and B5 in which the number of clusters is three.

Again, the proposed method performs both qualita-

tively and quantitatively better than the other four

methods. Although FGFCM has somewhat compara-

ble segmentation results with our method on synthetic

images, Fig. 3 shows that the performance difference

of the proposed method in real images is even greater.

Our method performs better in the segmentation of the

most compact regions. Table 3 provides the SA metric

evaluation of the segmented images shown in Fig. 3.

According to this table, the method that has close per-

formance to our method is not merely FGFCM. Sur-

prisingly, FCM has the second best performance in

B5, and also a close performance to FGFCM in B6.

5 CONCLUSIONS AND FUTURE

WORK

A noisy image segmentation method was proposed

using PSO and FCM. The main objectives were to in-

troduce a new algorithm that is parameter free, has

good performance on impulse noises, and can deal

with heavy density noise. In this way, modifying the

traditional Euclidean similarity measure in FCM us-

ing different intensity-based features extracted from a

neighboring window around each pixel was the main

objective. PSO was utilized to produce an optimum

combination of these features, and FCM was used to

deal with the clustering problem. Spatial, intensity,

and fuzzy criteria are considered in the new similar-

ity metric simultaneously for better performance. The

proposed method introduces a new algorithm to com-

bine different features extracted from the local neigh-

boring window. This puts forward a new way to fuse

features of different types. A future work in this man-

ner is to use more effective features extracted form

the neighboring window. Features than can extend the

applicability of the proposed method to other types of

noises as well. The qualitative and quantitative eval-

uation showed better performances compared with a

few state-of-the-art methods.

REFERENCES

Ahmed, M., Yamany, S., Mohamed, N., and Farag, A.

(1999). A Modiﬁed Fuzzy C-Means Algorithm for

MRI Bias Field Estimation and Adaptive Segmenta-

tion. In Taylor, C. and Colchester, A., editors, Med-

ical Image Computing and Computer-Assisted Inter-

vention – MICCAI’99, volume 1679 of Lecture Notes

in Computer Science, pages 72–81. Springer Berlin

Heidelberg.

Ant

uNez, E., Marﬁl, R., Bandera, J. P., and Bandera, A.

(2013). Part-based object detection into a hierarchy of

image segmentations combining color and topology.

Pattern Recogn. Lett., 34(7):744–753.

Benaichouche, A., Oulhadj, H., and Siarry, P. (2013). Im-

proved spatial fuzzy c-means clustering for image

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

segmentation using {PSO} initialization, mahalanobis

distance and post-segmentation correction. Digital

Signal Processing, 23(5):1390 – 1400.

Bovik, A. C. (2005). Handbook of Image and Video Pro-

cessing (Communications, Networking and Multime-

dia). Academic Press, Inc., Orlando, FL, USA.

Cai, W., Chen, S., and Zhang, D. (2007). Fast and ro-

bust fuzzy c-means clustering algorithms incorporat-

ing local information for image segmentation. Pattern

Recognition, 40(3):825–838.

Chen, S. and Zhang, D. (2004). Robust image segmenta-

tion using fcm with spatial constraints based on new

kernel-induced distance measure. Systems, Man, and

Cybernetics, Part B: Cybernetics, IEEE Transactions

on, 34(4):1907–1916.

Dunn, J. C. (1973). A Fuzzy Relative of the ISODATA Pro-

cess and Its Use in Detecting Compact Well-Separated

Clusters. Journal of Cybernetics, 3(3):32–57.

Eberhart, R. and Kennedy, J. (1995). A new optimizer using

particle swarm theory. In Micro Machine and Human

Science, 1995. MHS ’95., Proceedings of the Sixth In-

ternational Symposium on.

Engelbrecht, A. P. (2007). Computational Intelligence: An

Introduction. Wiley Publishing, 2nd edition.

Ferrari, V., Tuytelaars, T., and Van Gool, L. (2006). Simul-

taneous Object Recognition and Segmentation by Im-

age Exploration. In Ponce, J., Hebert, M., Schmid, C.,

and Zisserman, A., editors, Toward Category-Level

Object Recognition, volume 4170 of Lecture Notes

in Computer Science, pages 145–169. Springer Berlin

Heidelberg.

Hathaway, R., Bezdek, J., and Hu, Y. (2000). Gener-

alized fuzzy c-means clustering strategies using lp

norm distances. Fuzzy Systems, IEEE Transactions

on, 8(5):576–582.

Kang, Y., Yamaguchi, K., Naito, T., and Ninomiya, Y.

(2011). Multiband image segmentation and object

recognition for understanding road scenes. Intelli-

gent Transportation Systems, IEEE Transactions on,

12(4):1423–1433.

Kennedy, J. and Eberhart, R. (1995). Particle swarm op-

timization. In Neural Networks, 1995. Proceedings.,

IEEE International Conference on, volume 4, pages

1942–1948 vol.4.

Krinidis, S. and Chatzis, V. (2010). A robust fuzzy local in-

formation c-means clustering algorithm. Image Pro-

cessing, IEEE Transactions on, 19(5):1328–1337.

Lim, J. S. (1990). Two-dimensional Signal and Image Pro-

cessing. Prentice-Hall, Inc., Upper Saddle River, NJ,

USA.

Mahalingam, T. and Mahalakshmi, M. (2010). Vision based

moving object tracking through enhanced color image

segmentation using haar classiﬁers. In Proceedings

of the 2nd International Conference on Trendz in In-

formation Sciences and Computing, TISC-2010, pages

253–260.

Martin, D., Fowlkes, C., Tal, D., and Malik, J. (2001).

A database of human segmented natural images and

its application to evaluating segmentation algorithms

and measuring ecological statistics. In Proc. 8th Int’l

Conf. Computer Vision, volume 2, pages 416–423.

Mei, X. and Lang, L. (2014). An image retrieval algorithm

based on region segmentation. Applied Mechanics

and Materials, 596:337341. cited By 0.

Mirghasemi, S., Sadoghi Yazdi, H., and Lotﬁzad, M.

(2012). A target-based color space for sea target de-

tection. Applied Intelligence, 36(4):960–978.

Szilagyi, L., Benyo, Z., Szilagyi, S., and Adam, H. (2003).

Mr brain image segmentation using an enhanced fuzzy

c-means algorithm. In Engineering in Medicine and

Biology Society, 2003. Proceedings of the 25th An-

nual International Conference of the IEEE, volume 1,

pages 724–726 Vol.1.

Tian, X., Jiao, L., and Zhang, X. (2013). A clustering al-

gorithm with optimized multiscale spatial texture in-

formation: application to SAR image segmentation.

International Journal of Remote Sensing, 34(4):1111–

1126.

Tran, D., Wu, Z., and Tran, V. (2014). Fast Generalized

Fuzzy C-means Using Particle Swarm Optimization

for Image Segmentation. In Loo, C., Yap, K., Wong,

K., Teoh, A., and Huang, K., editors, Neural Infor-

mation Processing, volume 8835 of Lecture Notes in

Computer Science, pages 263–270. Springer Interna-

tional Publishing.

Wiener, N. (1964). Extrapolation, Interpolation, and

Smoothing of Stationary Time Series. The MIT Press.

Zhang, J.-Y., Zhang, W., Yang, Z.-W., and Tian, G. (2014).

A novel algorithm for fast compression and recon-

struction of infrared thermographic sequence based on

image segmentation. Infrared Physics & Technology,

67(0):296–305.

Zhang, Q., Huang, C., Li, C., Yang, L., and Wang, W.

(2012). Ultrasound image segmentation based on

multi-scale fuzzy c-means and particle swarm opti-

mization. In Information Science and Control Engi-

neering 2012 (ICISCE 2012), IET International Con-

ference on, pages 1–5.

Zhang, Q., Kamata, S., and Zhang, J. (2009). Face detection

and tracking in color images using color centroids seg-

mentation. In Robotics and Biomimetics, 2008. RO-

BIO 2008. IEEE International Conference on, pages

1008–1013.

Zhuang, H., Low, K.-S., and Yau, W.-Y. (2012). Multichan-

nel pulse-coupled-neural-network-based color image

segmentation for object detection. Industrial Elec-

tronics, IEEE Transactions on, 59(8):3299–3308.

A Heuristic Solution for Noisy Image Segmentation using Particle Swarm Optimization and Fuzzy Clustering