Development of an Evolutionary Algorithm for Design of Electron

Guns for Material Processing

Colin Ribton

1,2

and Wamadeva Balachandran

College of Engineering Design and Physical Sciences, Brunel University London, West London, U.K.

Electron Beam Section, TWI Ltd, Granta Park, Abington, Cambridge, U.K.

Keywords: Optimisation, Electron, Modelling, Evolution.

Abstract: The design of high quality electron generators is important for a variety of applications including materials

processing systems (including welding, cutting and additive manufacture), X-ray tubes for medical,

scientific and industrial applications, microscopy, and lithography for integrated circuit manufacture. The

many variants of electron gun required, and the increasing demands for highly optimised beam qualities,

demands more systematic optimisation methods than offered by trial and error design approaches. This

article describes the development of evolutionary algorithms to enable the automatic optimisation of the

design of vacuum electron guns. The gun design usually is required to meet specified beam requirements for

the applications of interest, so within this work, beam characteristics from the calculated electron

trajectories, for example brightness, intensity at focus and beam angle, were derived and used as a measure

of the design fitness-for-purpose. Evolutionary parameters were assessed against the efficiency and efficacy

of the optimisation process using an analogous design problem. This novel approach offers great potential

for producing the next generation of electron guns.

1 INTRODUCTION

The design of electron guns is typically carried out

with analysis software tools to test whether

prospective designs will meet the design

requirements. As such, the design of guns is at best

an informed trial-and-error process. Using present

techniques, the final design settled upon may not be

the best available, and may just be a local optimum

for the feature and dimension changes attempted.

Confidence that the best design has been found can

be increased by carrying out further analysis of

different designs, but this can be time consuming

and ultimately not satisfactory.

Requirements for electron guns are generally

specified as beam parameters suitable for the

application (ISO 2008). Typically, this would be a

required intensity at a certain working distance from

the end of the gun column, or a range of required

values – but the beam angle may also be important

too. For example, lower angles are specified for

thick section welding applications so that the beam

is intense through the thickness of the weld, whereas

for thin section welding the beam angle can be

higher, as a more shallow depth of focus can be

tolerated. Normally an electron gun will be designed

to be suitable for a range of applications, so the

beam requirements may be stated as a list of

intensity and power at a working distance. The

accelerating potential is influential on the beam

characteristics but usually this parameter has a fixed

maximum for a particular application, constrained

by the specification of high voltage components and

X-ray shielding. In design optimisation terminology,

electron guns have many variables of geometry and

electrical operation, and are likely to have multiple

objectives in all but the simplest of cases.

The primary challenge addressed by this work is

to assess how automated design evolution

methodologies can be successfully applied to

electron gun designs.

Within this work, techniques have been

developed for quantifying the electron optical

properties of beams produced by analytical

simulations of prospective gun designs. A

methodology has been developed to automatically

generate electron gun models, which give accurate

prediction of electron trajectories. Methods for

encoding the design have been developed and tested

– potentially allowing a variety of optimisation

techniques to be applied.

138

Ribton, C. and Balachandran, W..

Development of an Evolutionary Algorithm for Design of Electron Guns for Material Processing.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 138-148

ISBN: 978-989-758-157-1

The focus of this work was upon an evolutionary

method for optimisation of designs to enable

automatic design of electron guns to meet specified

requirements within defined geometric and electrical

constraints. The aim was to develop a method

whereby a designer can identify beam requirements

and system constraints, which are then used to find

an optimum electron gun geometry.

The aims of the work were as follows.

• To investigate the best way of assessing and

quantifying the beam quality over the operational

range of the gun.

• To develop an optimisation methodology for

design of electron guns – in particular the use of an

evolutionary design technique that will use the

quantified beam characteristics as a quality factor

• To carry out a case study where the

methodology will be applied to an electron gun

design with the aim of demonstrating the viability of

the design process.

2 BACKGROUND

2.1 Meta-heuristic Optimisation

Methods

There are many variants of optimisation techniques

that have been applied to engineering design

(Sykulski, 2008). Design problems typically may be

characterised as having multiple input variables

where no assumptions can be made about their

relationship to the solution, i.e. the solution function

cannot be assumed be of any type, and cannot be

assumed to be continuous. In addition, many

problems will have local optima. The solution is

often found by using computer modelling to

simulate the candidate solution, with quantified

outputs being derived from the model to assess its

suitability. Where no assumptions can be made

regarding the solution function, meta-heuristic

methods are used. Many of these have been

modified to explore the input variables’ ranges more

widely to avoid being ‘trapped’ in local optima.

Optimisation methods include simulated annealing

(Kirkpatrick et al., 1983), particle swarm

optimisation (Clerc, 1999) and ant colony

optimisation (Dorigo et al., 1999).

Where there are multiple objectives (measures of

fitness) it is likely that no one solution will optimise

all of these. Consequently, there are a set of optimal

solutions that are equally weighted. If a

representative sub-set of these is plotted in objective

space, a Pareto front is displayed (Hawe and

Sykulski, 2007). All solutions on the front are

equally optimal and none of them could be improved

in one objective without another objective being

diminished. Selecting one of the solutions can then

only be carried out by applying another measure of

fitness, or by a subjective choice.

Evolutionary algorithms (Denies et al., 2013) use

processes of selection, mutation and reproduction to

attempt to find an optimal design. Variables for the

candidate solutions must be encoded in a set of

genes. The solutions are analysed, scored according

to the design requirements and a sub-set of the best

designs is selected. The processes of inheritance,

genetic cross-over, and mutation are applied to

generate a new population of candidate solutions.

Normally, the population is generated initially as a

random set of solutions and then with each

generation the fittest are selected to parent the next

generation. The process continues until a satisfactory

solution is generated.

For the reported work evolutionary algorithms

were investigated for electron gun design for the

first time. The optimisation process can be formally

stated as follows. Tentative designs are fully

described genetically. The function:



(



)

:Φ



→ℝ

assigns real values to genes, see section 3.2,

where Φ



represents the genotypic search space. The

optimal solution  is found from

=max

∈



()

where 

(



)

is the objective function to be

maximised (Franz 2006).

In the case of electron guns this is a non-

continuous function with many local maxima. In this

work the objective function is derived from electron

optical characteristics of the beam produced by the

design, and these are calculated by modelling the

tentative solution x in finite element software to find

field and charge distributions, ray tracing and then

electron optical calculation, see section 3.1.

2.2 Electron Gun Design

Successful gun design requires calculation of

electron emission and the focusing of electron beams

that can be achieved as they are accelerated. High

voltage and high power electron beams for material

processing applications were first demonstrated

during the late 1940s and 1950s by Steigerwald in

Germany, Stohr in France and Wyman in the USA

prior to the availability of computer modelling

software.

Development of an Evolutionary Algorithm for Design of Electron Guns for Material Processing

139

The higher current beams required new design

approaches to avoid beam aberration due to the

mutual repulsion of the electrons, particularly as

they are first emitted from the cathode. In particular,

the Pierce gun geometry was developed that used

focusing electrostatic fields to overcome the beam

spreading caused by space charge (Pierce, 1954).

As computing power became available, the first

electron optical software for the design of guns and

optics was developed initially for accelerator

experiments – notably at Stanford University in

USA (SLAC) (Herrmannsfeldt, 1988) and

Rutherford Appleton Laboratories (RAL)

(Biddlecombe and Simkin, 1983). Computer

analysis of electron gun designs allowed production

of higher beam powers. Highlights included

developments during the 1970’s and 1980’s at

Steigerwald, Sciaky and TWI.

The design of electron guns, lenses and

deflection systems has advanced significantly since

the introduction of computer modelling of

electrostatic and electromagnetic systems. In

particular, development of high power guns used for

welding and melting, where space charge plays a

significant role in determining the beam qualities,

has depended upon accurate modelling. The

programs from SLAC and RAL have been

developed further in scope and capacity, taking

advantage of computer hardware developments, and

are now available as EGUN and the Opera software

package respectively. There are now many other

electron gun analysis programs available. An

example of a 2D model solution is given in figure 1.

As the model is axisymmetric, only the right half is

shown. The cathode is positioned at Z=0 and the

beam emerges from the anode at Z=-50. In essence,

the software packages take as inputs the geometry,

the cathode electron emission characteristics and

applied potentials, and produce a set of electron

beamlet trajectories. These trajectories can be

analysed further to derive electron optical properties

of the beam – see section 3.

Mathematical analysis techniques have been

applied to optimise the curvature of cathodes in

electron guns (Lewis et al., 2004), and these have

been shown to be effective. It may be possible to

develop further these techniques to look at the

combined shape of the gun electrodes and cathode,

however the complexity of the problem space, and

the number of possible combinations, may extend

computing times beyond reasonable durations.

Figure 1: Example of a 2D solution of an electron gun

showing the geometry in cross section and the electron

beamlet trajectories.

For highly constrained variables, response

surface modelling techniques such as kriging (Hawe

and Sykulski, 2007), (Lebensztajn et al., 2004) have

been deployed. Kriging is a method originally

developed for geo-statistical modelling. It has been

applied to electromagnetic problems to interpolate

between known values in order to find an optimum

value – for example to optimise the pole piece

profile to produce a required magnetic field

distribution.

This approach is most suitable for investigating

minor changes to geometry, where the variation is

reasonably constrained and where a continuously

variable optimisation function is experienced.

Evolutionary algorithms, by comparison, are far

more flexible in dealing with a more complicated

solution space, and far more capable of searching

across several local maxima for an optimal solution.

Very recently published work has looked at

shape optimisation using evolutionary algorithms for

a magnetron injection gun (Jiang et al., 2015). In this

work the objective function optimised the electron

velocity spread. The reported work differs in using

processing beam characteristics for the objective

function, which takes into account the electron

optics and processing requirements rather than direct

use of the output from an electron gun model.

In summary, many different optimization

techniques are available. Prior to this work, only

kriging has been applied to processing electron gun

design, and this in a limited fashion.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

140

3 AN OPTIMISATION METHOD

FOR ELECTRON GUN DESIGN

3.1 Beam Quality Metrics

Any optimisation method will require a quantified

measure of the suitability of the design to meet the

specified requirements. In the case of electron gun

design, it is important therefore to derive beam

quality metrics as a gauge for the design fitness.

Within this work a space charge solver and electron

trajectory plotting software package has been used to

analyse designs. It was then necessary to derive the

beam characteristics from the electron trajectories

from the analysis. These were required to be in a

form that could then be gauged against

requirements.

It was necessary to analyse any one design over a

number of different operating conditions, e.g.

varying cathode emissivity and accelerating

potentials, to ensure that the design requirements

were met over the working range of the gun. The

scoring system was required to combine assessment

of the operation at all the different conditions.

For materials processing applications there are a

number beam characteristics of particular relevance.

For example, in electron beam welding, where the

beam penetrates into material thicknesses that can be

up to several hundred millimetres, the ability of the

beam to form a vapour filled deep cavity (referred to

as a keyhole) is dependent upon its intensity. In

addition, the depth of focus of the beam, which is

related to the beam angle, typically will be of greater

importance for thicker section welding. Brightness is

an inherent quality of an electron beam, and is

defined as the ratio of the focused spot intensity to

the beam solid angle. High brightness indicates that

an intense and near parallel beam could be formed

by the right electron optical elements. It also

indicates that a very intense spot could be formed for

a high angle beam.

The use of beam brightness alone as a score of

the gun design may lead to impractical designs

where the beam produced was of such high diameter

that the lens and deflection coils became too large.

Consequently, the scoring system needed to combine

a number of factors, such as brightness and beam

width in the lens. These factors were weighted

according to their relative importance. Some of the

additional factors required the electron beam to be

analysed after the focusing lens – for example to

look at the focused beam spot size at the work piece.

Within this work 2-D models of the electron gun

were used and trajectory plotting was carried out in

two dimensions. This is accurate for the vast

majority of electron guns used for materials

processing, which are axi-symmetric. The

trajectories produced by the analysis software were

described by a velocity vector and radial position

when at a specified axial position beyond the anode.

Each trajectory carries a portion of the beam current,

and this information is also extracted. This can be

used in current weighted average calculations of the

beam radius and angle. The solution time for a

single model was typically less than 1 minute.

Although the beam could have been examined

after the lens by modelling the complete gun

column, this would have been computationally

expensive, leading to extended solution times. To

speed up the analysis, algorithms have been

developed that allowed the beam trajectories to be

projected forward and through the focusing lens. For

most materials processing electron beam systems the

lens aberration could be neglected and it was

therefore not necessary to model the magnetic lens

field and plots the trajectories of the beam through

it. In addition, errors accumulate with trajectory

plotting such that plotting overlong path lengths

would be inaccurate. Instead, a mathematical model

of the lens was used and the trajectories calculated

from the gun, through the lens to their focal position

at the work piece. Intensity plots across the focused

beam spot were then calculated which allowed beam

intensity metrics to be derived such as the full width

at half maximum (FWHM), the full width at half

power (FWHP) and the current weighted average

(CWAD) diameter, see for example figure 2. A

useful metric of beam quality is given by the

brightness, defined as

=



where J is the beam spot intensity and Ω is the

beam solid angle. This quality is invariant, in

practical terms, for material processing type electron

guns, as the electron lens aberration is comparatively

insignificant.

Consequently, a number of beam metrics were

derived from the trajectory files, which could then

be used subsequently as a measure of the gun design

fitness in order to enable selection of better designs

within a population as part of a design evolutionary

algorithm.

Development of an Evolutionary Algorithm for Design of Electron Guns for Material Processing

141

Figure 2(a): Example of a ray diagram after projection of trajectories from the gun model through a mathematical lens to

their focus at the work piece.

Figure 2(b): Example of a beam intensity plot after projection of trajectories from the gun model through a mathematical

lens to their focus at the work piece.

3.2 Genetic Coding of the Design

To apply evolutionary design techniques it is

necessary to include the design into a genome. The

genome is a collection of genes that describe the

design. For an electron gun, designed in 2-D, a

geometry was specified describing the anode, high-

voltage electrodes and the cathode. Each line within

the geometry had a starting and stopping position

and a degree of curvature. These parameters

provided a means of describing the geometry as a

series of genes. An example of the geometric

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

142

description is given in Table 1, which could be

directly translated into a model by the simulation

software. Each row in Table 1 described the next

corner of an electrode, cathode or anode shape. The

corner coordinates were given as real values, XP and

YP, and the discretisation of the line, which gave

higher mesh resolution for curved lines for example,

was given by the parameter N. Other parameters that

were not varied by the evolutionary algorithm were

also defined e.g. F, which was the boundary

condition for the model at that face.

Table 1: Example of geometric description of part of an

electrode in an electron gun.

1 CARTESIAN YP=-38.7 CURVATURE=0 N=17

XP=7.95

2 CARTESIAN XP=100 N=93 YP=-38.7

CURVATURE=0.0

3 CARTESIAN YP=-50 N=12 F=NO XP=100.0

CURVATURE=0.0

4 CARTESIAN XP=2.75 N=98 YP=-50.0

CURVATURE=0.0

5 FINISH N=12 F=V

6 QUITDRAW

7 GROUP NAME=ANODE

Each of the shapes within the gun design were

defined in a similar manner to Table 1, and together

these formed the complete genotype.

The special adaptions that have been made to

evolutionary methods to allow them to be

implemented for electron gun designs were:

• A change genome was constructed that

contained only those parts of the design that can be

changed and to which evolutionary processes can be

applied

• A generic genome was constructed that

described the rest of the design, and which when

added to the change genome described a complete

gun design

• The allowable range of any position or line

curvature in the change genome was encoded within

it to (a) constrain solutions within practical limits

and (b) scale any mutation to that range

• Gene splitting was only carried out between

genes so that mutation could be controlled

discretely.

There were a number of constraints on the

geometry that could be accommodated. The

approach taken within this work to recognise these

constraints was to take, in preparation for the design

optimisation algorithm, two geometries which

described the full range of design freedom. These

two geometries were examined by an algorithm to

produce a ‘change genome’ containing just those

parts of the model that were different in the two

geometries. Those parts of the model that were

completely constrained, i.e. the same in the two

geometries were not genetically encoded. These

were described within a template similar to Table 1

and recorded in a single generic genome to be used

for all the designs.

The change genome was used whenever a gene

was mutated. The mutation was constrained within

the limits for that position or line curvature and the

scale of mutation was normalized to the range for

that position or curvature. Combining the new

genome with the generic genome gave a description

of the complete gun design.

The following steps were carried out to

implement the design evolution process:

i. An initial population of electron gun design

variants was generated by producing genomes

made from a randomised set of change

genomes combined with the generic genome.

ii. Each of the electron gun designs was analysed

using a finite element space-charge solver and

electron trajectory vectors for beamlets from

the cathode determined as they left the gun

iii. For each of the electron gun designs, the

electron trajectory data was used to produce

beam quality metrics (brightness, intensity,

angle and beam width) through calculation of

the trajectory path mathematically traced

through an electron lens to the work piece

iv. The beam quality metrics were then used to

derive a fitness score for the design. This score

depended upon the requirements for the gun

e.g. maximise the beam brightness and

minimise the beam angle

v. Those designs with the best fitness score were

selected to produce a ‘parent group’

vi. The next generation of designs was produced

from this group by choosing two designs

randomly and splicing a random section of one

change genome into the other. The genome was

only split between genes to avoid mutations

caused by splits occurring within a gene.

Random mutation of any one of the change

genes was also implemented in this stage. The

new change genomes were combined with the

generic genome to produce the new generation

of gun designs.

vii. The parent group and the new generation

formed a new population, which was then put

through the same process until a preselected

satisfactory fitness score was achieved.

The process therefore was designed to have a

number of features anticipated to be of benefit to the

Development of an Evolutionary Algorithm for Design of Electron Guns for Material Processing

143

particular challenge. A good design genome was

promoted to the population forming the next

generation until its fitness score ranking was not

high enough. This ensured that each generation’s

parent group was at least as good as the last, and is a

process termed elitist selection. This feature has

been investigated, as there was concern that elitism

may allow local maxima of the optimisation function

to dominate.

By splicing the genes from two parents, a section

of the design was copied to the child with the rest

remaining the same as one of the parents. In genetic

algorithm terminology this was a two point

crossover function. The splicing respected the

database structure of the genome to avoid mutation

of the design due to corrupting the database. This

was achieved by using ensuring that the data format

as represented in Table 1 was maintained. However,

some mutation was introduced to a controlled level

to ensure that the design space was adequately

explored.

In summary, the evolutionary process was

implemented with special adaptions to make it

suitable for electron gun design using modelling

software and working within practical physical

constraints.

3.3 Evolution Parameters

The main parameters for the evolution process were

the parent group size, the offspring group size, the

probability of gene mutation and the scale of gene

mutation. These parameters generally determine the

efficiency of the optimisation process, i.e the time

taken for optimisation and the exploration of the

problem space. Although many publications quote

the evolution parameters used, there is little

justification for the choices taken (Karafotias et al.

2014). Within this work, an analogous design

problem to electron guns has been used to examine

the effect of different parameters on the evolutionary

optimisation process.

The analogous problem chosen is one of shape

fitting. The problem is to find the coordinates of the

corners of a target shape. The fitness function is the

inverse of the sum of the distances of mismatch

between the potential solution corners and the target

shape corners.

This problem is useful for examining the effect

of evolutionary parameters because it is dealing with

coordinate values, as in the electron gun

optimisation. It is also scalable in terms of

complexity – so the effect of increasing the number

of corners in the target shape can be examined.

This problem differs from electron gun design

optimisation in that the fitness function has a single

solution and varies smoothly, which would not be

expected for an electron gun being scored on the

electron beam optical qualities. However, tests

carried out with this problem, described in section 4,

give an insight into identifying the best evolutionary

parameters for optimisation.

4 DESIGN TRIALS

4.1 Shape Evolution

The objective of this trial was to determine the most

efficient settings of the evolutionary parameters for

solving a shape fitting optimisation. This has been

carried out for 3, 5, 8 and 10 cornered shapes. For 13

cornered shapes, the individual optimisations were

taking too long to allow practical trials over a wide

range of evolutionary parameters. Efficiency was

measured by recording the total number of calls to

the scoring function for each optimisation – this

must be done for the initial parent group and each

generation of offspring. In the analogous electron

gun design optimisation, a call to the scoring

function would require a model solution and

trajectory analysis, taking up to 1 minute. In this

case, a call to the scoring function took under 1msec,

allowing a large number of trials to be carried out.

For the 3 to 10 cornered shapes, the number of

offspring has been varied from 2 to 100, the parent

group from 2 to 30, the mutation scale from 0.05 to

1 (5% to 100%) and the mutation rate from 0.01 to

0.1 (1% to 10%). In total, the different combination

of parameters led to 42,000 optimisations being

executed for each shape. Each optimisation required

from 338 (fastest 3 cornered) to over 200,000 calls

(slowest 10 cornered) to the scoring function.

The results were analysed by plotting the number

of calls as a function of the number of offspring and

number in the parent group, see figure 3(a) and the

mutation rate and mutation scale, see figure 3(b),

both for 10 cornered shape evolution. Also,

sampling was carried out of the most efficient 1% of

optimisations for each shape and the modal

evolutionary parameter settings were extracted – see

figures 4(a) and (b).

The results show that a small parent group of 2

or 4 is most efficient over all the range of shapes. It

is also clear that as the number of corners increases

the optimum values for mutation rate decreases. For

3 and 5 cornered shapes the optimum mutation scale

is 0.15 dropping to 0.1 for 8 and 10 cornered shapes.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

144

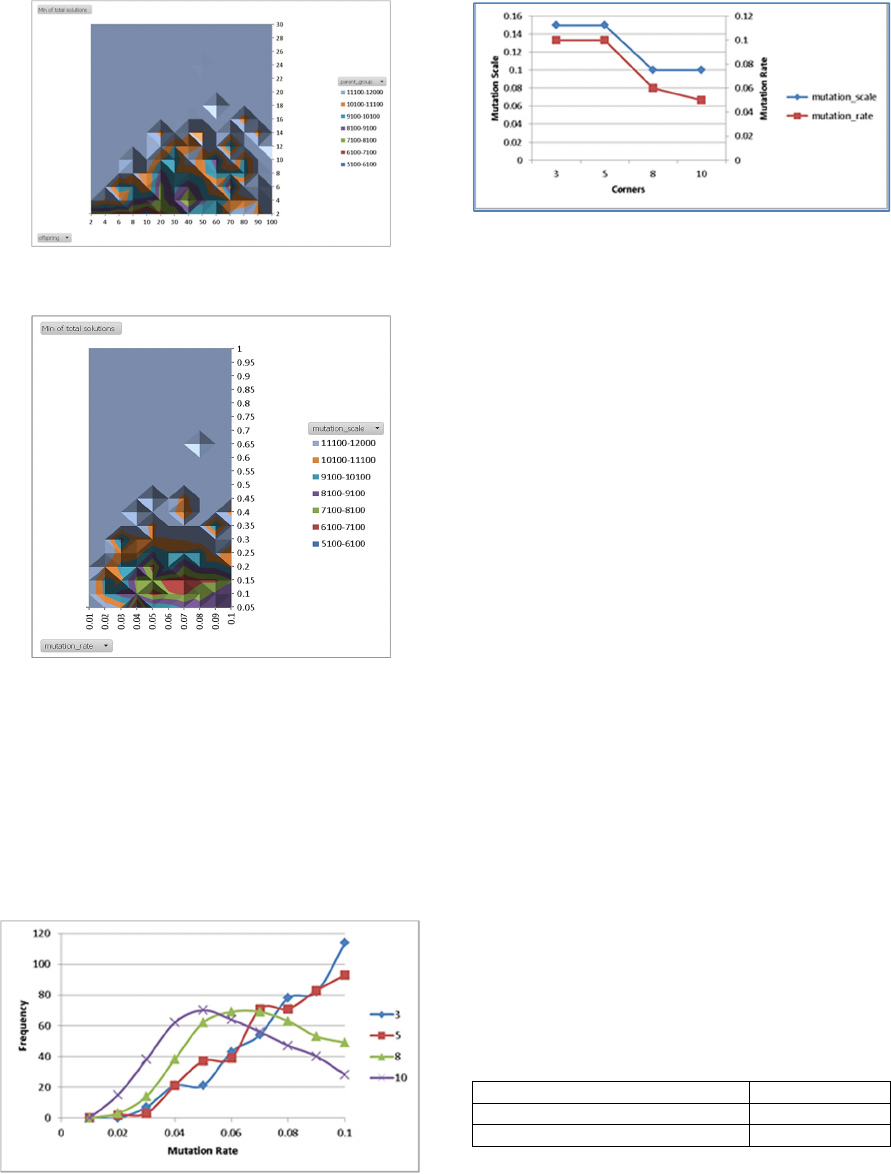
Figure 3(a): The number of score function calls as a

function of the parent group and offspring group sizes.

Figure 3(b): The number of score function calls as a

function of the mutation scale and mutation rate.

For 3 cornered shapes the optimum mutation rate is

0.1, decreasing to 0.06 for 8 cornered shapes and

0.05 for 10 cornered shapes. This is shown in figures

4(a) and (b).

In summary, this trial has shown that as problem

complexity increases the optimum mutation rate and

scale for rapid optimisation will be lower. It

Figure 4(a): Histogram of the top 1% optimisations

showing decreasing mutation rate with increasing problem

complexity.

Figure 4(b): Modal values of mutation scale and mutation

rate of the top 1% efficient optimisations.

indicates that values of mutation rate and scale

should be used of less than 0.05 and 0.1

respectively. Regardless of problem complexity,

parent groups of 2 or 4 are the most efficient, as are

offspring numbers of 10 or less.

These results were then used to determine the

evolutionary parameters for an electron gun design

problem.

4.2 Anode Shape Evolution

The electron gun evolutionary design process was

applied to a novel radio frequency (RF) excited

plasma cathode gun design (del Pozo et al., 2014;

Ribton and Sanderson, 2012). This type of gun

design is a diode having a high-voltage electrode

and cathode at the same potential. The cathode is a

plasma, but for simulation purposes the cathode

surface has been modelled as a lanthanum

hexaboride thermionic emitter over a range of

temperatures and therefore emissivities, producing

electrons with no thermal energy.

The gun design was required to produce an

intense electron beam at focus, therefore of high

brightness, and produce a reasonably low angle

beam so that it could pass through an existing gun

column with a constriction at the electron lens.

However, too low an angle beam would give poor

electron optic magnification so an optimum beam

diameter of 4mm at the lens position (150mm from

the cathode) was chosen. These requirements are

summarised in Table 2.

Table 2: RF plasma gun beam requirements.

Metric Requirement

Diameter at 150mm from cathode Ideally 4mm

Brightness > 5000 Amm

-2

-1

Weighting factors were used for each of the metrics

as the design fitness test needed to look at more than

one requirement in order to allow ranking of the

Development of an Evolutionary Algorithm for Design of Electron Guns for Material Processing

145

design variants in the population. The scoring

function is described in the following pseudo-code:

Over the cathode temperature range

1450 – 1600K and for 30kV and 60kV

accelerating potentials:

score = add Log(brightness)*beam

current

If beam current <20mA

If 1/(beam diameter 150mm from

cathode – 4) >10

Add 10

Else

add abs(1/(beam diameter 150mm from

cathode – 4))

The evolution parameters used in this trial are

presented in Table 3.

Table 3: Evolutionary algorithm parameters.

Parameter Value

Parent group size 4

Offspring group size 6

Mutation scale 0.1

Mutation probability 0.07

Table 4(a): 1st Generation population ranked scores.

Model Score

Gen_0_Pop_1 2.37

Gen_1_Pop_6 2.10

Gen_1_Pop_4 2.10

Gen_0_Pop_3 2.09

Gen_1_Pop_5 2.09

Gen_0_Pop_0 2.03

Gen_1_Pop_7 2.02

Gen_1_Pop_8 2.02

Gen_0_Pop_2 2.01

Gen_1_Pop_9 2.01

Table 4(b): 10th Generation population ranked scores.

Model Score

Gen_10_Pop_4 11.59

Gen

Pop

43.57

Gen

Pop

63.57

Gen_9_Pop_5 3.57

Gen

Pop

63.57

Gen

Pop

73.57

Gen_9_Pop_7 3.23

Gen

Pop

53.03

Gen

Pop

82.89

Gen_10_Pop_9 2.65

The designs were labelled with a generation number

and a population number, e.g. Gen_1_Pop_5 was the

5th offspring produced in the first generation. A log

was kept of the scoring – this is shown for the 1st

generation in Table 4 (a) and for the 10th generation

in Table 4 (b).

The progress of the automatic design algorithm

was monitored through the plotting the best fitness

score of each generation. This is presented in Fig 5.

Figure 5: The best fitness score in successive generations.

The use of an evolutionary algorithm for the

electrode optimisation allowed designs meeting the

requirements to be found within 2 to 3 hours of

computing time without human expert intervention.

This compares well with normal trial and error

design requiring frequent expert intervention over a

period of 10 to 15 hours. The ability to template

constrained parts of the design was useful in

ensuring that the algorithm only explored

mechanically viable designs making it more

efficient. Further comparison with other

optimisation methods will be carried out in the

future as details of solution times for electron gun

optimisation methods are not published at this time

5 CONCLUDING REMARKS

Electron beam gun design is at best a trial and error

process. An evolutionary design algorithm has been

implemented which enables the automatic design of

an electron beam gun to produce electron beam with

characteristics to meet specified requirements. This

algorithm has been trialled on a novel RF excited

plasma cathode gun design and shows promising

results.

Analysing electron guns and deriving electron

beam characteristics is necessary within any

automatic design process in order to assess the

suitability of the design to meet requirements.

However, this is a process that uses substantial

computing resource. Until recently, the solution

times required meant that solving the large number

of designs that necessarily make up a population was

impractical on normal desktop computers and was

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

146

expensive if implemented on multicore

supercomputers. Current analysis software for

analysing electron beam guns in 2-D are relatively

fast. For example, a 10,000 element model of an

electron gun will converge to a solution, taking into

account the space charge of the electron beam, in a

time of less than 1 minute running on a desktop PC.

These recent advances in software implementation

and computing hardware have made the

implementation of automatic design algorithms

possible.

There are two key steps in implementing and

evolutionary algorithm for design: the design

features to be evolved must be encoded in a genome,

and the suitability of the design must be able to be

quantified in a fitness score. As such the

implementation of evolutionary algorithms for

design could be applied to a very wide range of

design challenges.

Within this work an evolutionary design

algorithm for electron guns was developed and

tested. As a single optimisation can take several

hours, the evolutionary parameters have been

estimated from an analogous problem of shape

fitting, where many thousands of solutions could be

analysed. In future work, more exploration of tuning

of evolutionary parameters will be carried out, and

automatic adjustment of the parameters at different

stages of the optimisation will be explored.

Monitoring of the score function for the best of

each generation shows incremental improvements

and on one occasion a significant jump going from

one generation to the next. In this work, the

optimisation process has been run several times and

this usually occurs, corresponding to a mutation or

gene spliced combination of features that gives a

near optimum diameter of beam in the lens and a

high brightness.

There are, however, a wide range of meta-

heuristic methods for design optimisation which

could be applied. At this time one of the most

popular and most promising methods is particle

swarm optimisation. The work carried out on

including the design and the software

implementation of an automatic design method will

in the near future be applied using alternative

optimisation techniques. It is also intended to

monitor the design optimisation convergence and

adjust the applied technique to converge at the

highest rate. This offers the tantalising possibility of

being able to optimise the optimisation method, for

example, the evolutionary process could itself

evolve to become ever more efficient.

From the work reported the following

conclusions can be drawn

• A technique has been developed to allow

electron gun designs to be automatically optimised

• Assessment of a gun design against required

electron beam characteristics has been quantified by

deriving key beam qualities from field analysis and

trajectory plotting

• An evolutionary design optimisation method

has been tested

• The design method has been applied to a novel

plasma cathode electron gun.

ACKNOWLEDGEMENTS

This work has been supported by The National

Structural Integrity Research Foundation, TWI Ltd

and Brunel University London.

REFERENCES

Biddlecombe, C. & Simkin, J., 1983. Enhancements to the

PE2D package. Magnetics, IEEE Transactions on,

19(6), pp.2635–2638.

Clerc, M., 1999. The swarm and the queen: towards a

deterministic and adaptive particle swarm

optimization. In Evolutionary Computation, 1999.

CEC 99. Proceedings of the 1999 Congress on.

Denies, J., Ahmed, H.B. & Dehez, B., 2013. Optimal

design of electromagnetic devices: development of an

efficient optimization tool based on smart mutation

operations implemented in a genetic algorithm.

Mathematics and Computers in Simulation.

Dorigo, M., Caro, G.D. & Gambardella, L.M., 1999. Ant

algorithms for discrete optimization. Artificial life,

5(2), pp.137–172.

Franz, R., 2006. Representations for genetic and

evolutionary algorithms. Springer-Verlag Berlin

Heidelberg.

Hawe, G. & Sykulski, J., 2007. Considerations of accuracy

and uncertainty with kriging surrogate models in

single-objective electromagnetic design optimisation.

Science, Measurement \& Technology, IET, 1(1),

pp.37–47.

Hawe, G.I. & Sykulski, J.K., 2008. A Scalarizing One-

Stage Algorithm for Efficient Multi-Objective

Optimization. IEEE Transactions on Magnetics, VOL.

44, NO. 6.

Herrmannsfeldt, W., 1988. EGUN: An electron optics and

gun design program.

ISO, 2008. Welding - Acceptance inspection of electron

beam welding machines - Part 1: Principles and

acceptance conditions.

Jiang, W. et al., 2015. Genetic Algorithm-Based Shape

Optimization of Modulating Anode for Magnetron

Development of an Evolutionary Algorithm for Design of Electron Guns for Material Processing

147

Injection Gun With Low Velocity Spread. IEEE

Transactions On Electron Devices, VOL. 62, NO. 8.

Kirkpatrick, S., Jr., D.G. & Vecchi, M.P., 1983.

Optimization by simulated annealing. Science,

220(4598), pp.671–680.

Karafotias, G., Hoogendoorn, M. & Eiben, A., 2014.

Parameter control in evolutionary algorithms: Trends

and challenges. IEEE Transactions on Evolutionary

Computation, to appear. Lebensztajn, L. et al., 2004.

Kriging: a useful tool for electromagnetic device

optimization. Magnetics, IEEE Transactions on, 40(2),

pp.1196–1199.

Lewis, B.M. et al., 2004. Design of an electron gun using

computer optimization. Plasma Science, IEEE

Transactions on, 32(3), pp.1242–1250.

Pierce, J.R., 1954. Theory and design of electron beams.

Del Pozo, S., Ribton, C. & Smith, D.R., 2014.

Characterisation of an RF excited argon plasma

cathode electron beam gun. In Vacuum Electron

Sources Conference (IVESC), 2014 Tenth

International. pp. 1–2.

Ribton, C. et al 2015. Plasma source apparatus and method

for generating charged particle beams. US Patent

9076626B2.

Sykulski, J.K., 2008. New trends in optimization in

electromagnetics. In Computation in Electromagnetics,

2008. CEM 2008. 2008 IET 7th International

Conference on. pp. 44–49.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

148