repAIrC: A Tool for Ensuring Data Consistency

By Means of Active Integrity Constraints

ıs Cruz-Filipe

, Michael Franz

, Artavazd Hakhverdyan

, Marta Ludovico

, Isabel Nunes

and Peter Schneider-Kamp

Dept. of Mathematics and Computer Science, University of Southern Denmark, Campusvej 55, 5230 Odense M, Denmark

Faculdade de Ci

encias da Universidade de Lisboa, Campo Grande, 1749-016 Lisboa, Portugal

Keywords:

Active Integrity Constraints, Database Repair, Implementation.

Abstract:

Consistency of knowledge repositories is of prime importance in organization management. Integrity con-

straints are a well-known vehicle for specifying data consistency requirements in knowledge bases; in partic-

ular, active integrity constraints go one step further, allowing the speciﬁcation of preferred ways to overcome

inconsistent situations in the context of database management.

This paper describes a tool to validate an SQL database with respect to a given set of active integrity con-

straints, proposing possible repairs in case the database is inconsistent. The tool is able to work with the

different kinds of repairs proposed in the literature, namely simple, founded, well-founded and justiﬁed re-

pairs. It also implements strategies for parallelizing the search for them, allowing the user both to compute

partitions of independent or stratiﬁed active integrity constraints, and to apply these partitions to ﬁnd repairs

of inconsistent databases efﬁciently in parallel.

1 INTRODUCTION

There is a generalized consensus that knowledge

repositories are a key ingredient in the whole pro-

cess of Knowledge Management, cf. (Duhon, 1998;

onig, 2012). Furthermore, being able to rely upon

the consistency of the information they provide is

paramount to any business whatsoever. Databases

and database management systems, by far the most

common framework for knowledge storage and re-

trieval, have been around for many years now, and

have evolved substantially, at pace with information

technology. In this paper, we are focusing on the im-

portant aspect of database consistency.

Typical database management systems allow the

user to specify integrity constraints on the data as

logical statements that are required to be satisﬁed at

any given point in time. The classical problem is

how to guarantee that such constraints still hold af-

ter updating databases (Abiteboul, 1988), and what

repairs have to be made when the constraints are vio-

lated (Katsuno and Mendelzon, 1991), without mak-

ing any assumptions about how the inconsistencies

came about. Repairing an inconsistent database (Eiter

and Gottlob, 1992) is a highly complex process; also,

it is widely accepted that human intervention is of-

ten necessary to choose an adequate repair. That said,

every progress towards automation in this ﬁeld is nev-

ertheless important.

In particular, the framework of active integrity

constraints (Flesca et al., 2004; Caroprese and

Truszczy

nski, 2011) was introduced more recently

with the goal of giving operational mechanisms to

compute repairs of inconsistent databases. This

framework has subsequently been extended to con-

sider preferences (Caroprese et al., 2007) and to ﬁnd

“best” repairs automatically (Cruz-Filipe et al., 2013)

and efﬁciently (Cruz-Filipe, 2014).

Active integrity constraints (AICs) seem to be a

promising framework for the purpose of achieving re-

liability in information retrieval:

• AICs are expressive enough to encompass the ma-

jority of integrity constraints that are typically

found in practice;

• AICs allow the deﬁnition of preferred ways to cal-

culate repairs, through speciﬁc actions to be taken

in speciﬁc inconsistent situations;

• AICs provide mechanisms to resolve inconsisten-

cies while the database is in use;

• AICs can enhance databases to provide a basis for

self-healing autonomic systems.

Cruz-Filipe, L., Franz, M., Hakhverdyan, A., Ludovico, M., Nunes, I. and Schneider-Kamp, P..

repAIrC: A Tool for Ensuring Data Consistency - By Means of Active Integrity Constraints.

In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 3: KMIS, pages 17-26

ISBN: 978-989-758-158-8

To the best of our knowledge, no real-world imple-

mentation of an AIC–enhanced database system ex-

ists today. This paper presents a prototype tool that

implements the tree–based algorithms for comput-

ing repairs presented in (Caroprese and Truszczy

nski,

2011; Cruz-Filipe et al., 2013). While not yet ready

for productive deployment, this implementation can

work successfully with database management sys-

tems working in the SQL framework, and is readily

extendible to other (nearly arbitrary) database man-

agement systems thanks to its modular design.

This paper is structured as follows. Section 2

recapitulates previous work on active integrity con-

straints and repair trees. Section 3 introduces our

tool, repAIrC, and describes its implementation, fo-

cusing on the new theoretical results that were nec-

essary to bridge the gap between theory and practice.

Section 4 then discusses how parallel computation ca-

pabilities are incorporated in repAIrC to make the

search for repairs more efﬁcient. Section 5 summa-

rizes our achievements and gives a brief outlook into

future developments.

2 ACTIVE INTEGRITY

CONSTRAINTS

Active integrity constraints (AICs) were introduced

in (Flesca et al., 2004) and further explored in (Carop-

rese et al., 2009; Caroprese and Truszczy

nski, 2011),

which deﬁne the basic concepts and prove complex-

ity bounds for the problem of repairing inconsistent

databases. These authors introduce declarative se-

mantics for different types of repairs, obtaining their

complexity results by means of a translation into re-

vision programming. In practice, however, this does

not yield algorithms that are applicable to real-life

databases; for this reason, a direct operational se-

mantics for AICs was proposed in (Cruz-Filipe et al.,

2013), presenting database-oriented algorithms for

ﬁnding repairs. The present paper describes a tool that

can actually execute these algorithms in collaboration

with an SQL database management system.

2.1 Syntax and Declarative Semantics

For the purpose of this work, we can view a database

simply as a set of atomic formulas over a typed

function-free ﬁrst-order signature Σ, which we will

assume throughout to be ﬁxed. Let At be the set of

closed atomic formulas over Σ. A database I entails

literal L, I |= L, if L ∈ At and L ∈ I , or if L is not a

with a ∈ At and a /∈ I .

An integrity constraint is a clause

,...,L

⊃ ⊥

where each L

is a literal over Σ, with intended se-

mantics that ∀(L

∧ . . . ∧ L

) should not hold. As

is usual in logic programming, we require that if L

contains a negated variable x, then x already occurs

in L

,...,L

i−1

. We say that I satisﬁes integrity con-

straint r, I |= r, if, for every instantiation θ of the vari-

ables in r, it is the case that I 6|= Lθ for some L in r;

and I satisﬁes a set η of integrity constraints, I |= η,

if it satisﬁes each integrity constraint in η.

If I 6|= η, then I may be updated through update

actions of the form +a and −a, where a ∈ At, stating

that a is to be inserted in or deleted from I , respec-

tively. A set of update actions U is consistent if it

does not contain both +a and −a, for any a ∈ At;

in this case, I can be updated by U, yielding the

database

I ◦ U = (I ∪

{

a | +a ∈ U

}

) \

{

a | −a ∈ U

}

The problem of database repair is to ﬁnd U such that

I ◦ U |= η.

Deﬁnition 1. Let I be a database and η a set of in-

tegrity constraints. A weak repair for hI ,ηi is a con-

sistent set U of update actions such that: (i) every

action in U changes I ; and (ii) I ◦ U |= η. A repair

for hI ,ηi is a weak repair U for hI ,ηi that is minimal

w.r.t. set inclusion.

The distinction between weak repairs and re-

pairs embodies the standard principle of minimality

of change (Winslett, 1990).

The problem of deciding whether there exists a

(weak) repair for an inconsistent database is NP-

complete (Caroprese and Truszczy

nski, 2011). Fur-

thermore, simply detecting that a database is incon-

sistent does not give any information on how it can be

repaired. In order to address this issue, those authors

proposed active integrity constraints (AICs), which

guide the process of selection of a repair by pairing

literals with the corresponding update actions.

In the syntax of AICs, we extend the notion of

update action by allowing variables. Given an action

α, the literal corresponding to it is lit(α), deﬁned as a

if α = +a and not a if α = −a; conversely, the update

action corresponding to a literal L, ua(L), is +a if

L = a and −a if L = not a. The dual of a is not a,

and conversely; the dual of L is denoted L

. An active

integrity constraint is thus an expression r of the form

,...,L

⊃ α

| ... | α

where the L

(in the body of r, body (r)) are literals

and the α

(in the head of r, head (r)) are update ac-

tions, such that



lit(α

)

,...,lit(α

)



⊆

{

,...,L

}

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

The set lit(head(r))

contains the updatable literals

of r. The non-updatable literals of r form the set

nup(r) = body (r) \ lit(head(r))

The natural semantics for AICs restricts the notion

of weak repair.

Deﬁnition 2. Let I be a database, η a set of AICs

and U be a (weak) repair for hI ,ηi. Then U is a

founded (weak) repair for hI ,ηi if, for every action

α ∈ U, there is a closed instance r

of r ∈ η such that

α ∈ head (r

) and I ◦ U |= L for every L ∈ body (r

) \



lit(α)



The problem of deciding whether there exists a

weak founded repair for an inconsistent database is

again NP-complete, while the similar problem for

founded repairs is Σ

-complete. Despite their natural

deﬁnition, founded repairs can include circular sup-

port for actions, which can be undesirable; this led

to the introduction of justiﬁed repairs (Caroprese and

Truszczy

nski, 2011).

We say that a set U of update actions is closed un-

der r if nup(r) ⊆ lit(U) implies head (r)∩U 6=

0, and

it is closed under a set η of AICs if it is closed under

every closed instance of every rule in η. In particular,

every founded weak repair for hI ,ηi is by deﬁnition

closed under η.

A closed update action +a (resp. −a) is a no-effect

action w.r.t. (I ,I ◦ U) if a ∈ I ∩ (I ◦ U) (resp. a /∈

I ∪ (I ◦ U)). The set of all no-effect actions w.r.t.

(I ,I ◦U) is denoted by ne(I ,I ◦ U). A set of update

actions U is a justiﬁed action set if it coincides with

the set of update actions forced by the set of AICs and

the database before and after applying U (Caroprese

and Truszczy

nski, 2011).

Deﬁnition 3. Let I be a database and η a set of

AICs. A consistent set U of update actions is a jus-

tiﬁed action set for hI ,ηi if it is a minimal set of up-

date actions containing ne (I ,I ◦ U) and closed un-

der η. If U is a justiﬁed action set for hI ,ηi, then

U \ ne(I ,I ◦ U) is a justiﬁed weak repair for hI , ηi.

In particular, it has been shown that justi-

ﬁed repairs are always founded (Caroprese and

Truszczy

nski, 2011). The problem of deciding

whether there exist justiﬁed weak repairs or justiﬁed

repairs for hI ,ηi is again a Σ

-complete problem, be-

coming NP-complete if one restricts the AICs to con-

tain only one action in their head (normal AICs).

2.2 Operational Semantics

The declarative semantics of AICs is not very sat-

isfactory, as it does not capture the operational na-

ture of rules. In particular, the quantiﬁcation over all

no-effect actions in the deﬁnition of justiﬁed action

set poses a practical problem. Therefore, an oper-

ational semantics for AICs was proposed in (Cruz-

Filipe et al., 2013), which we now summarize.

Deﬁnition 4. Let I be a database and η be a set of

AICs.

• The repair tree for hI ,ηi, T

hI ,ηi

, is a labeled

tree where: nodes are sets of update actions;

each edge is labeled with a closed instance of

a rule in η; the root is

0; and for each consis-

tent node n and closed instance r of a rule in η,

if I ◦ n 6|= r then for each L ∈ body (r) the set

= n ∪



ua(L)



is a child of n, with the edge

from n to n

labeled by r.

• The founded repair tree for hI ,ηi, T

hI ,ηi

, is con-

structed as T

hI ,ηi

but requiring that ua(L) occur

in the head of some closed instance of a rule in η.

• The well-founded repair tree for hI ,ηi, T

w f

hI ,ηi

, is

also constructed as T

hI ,ηi

but requiring that ua(L)

occur in the head of the rule being applied.

• The justiﬁed repair tree for hI ,ηi, T

hI ,ηi

, has

nodes that are pairs of sets of update actions

hU, J i, with root h

0i. For each node n and

closed instance r of a rule in η, if I ◦U

6|= r, then

for each α ∈ head(r) there is a descendant n

n, with the edge from n to n

labeled by r, where:

= U

∪

{

}

; and J

= (J

∪ {ua(nup(r))}) \

The properties of repair trees are summarized in

the following results, proved in (Cruz-Filipe et al.,

2013).

Theorem 1. Let I be a database and η be a set of

AICs. Then:

1. T

hI ,ηi

is ﬁnite.

2. Every consistent leaf of T

hI ,ηi

is labeled by a weak

repair for hI ,ηi.

3. If U is a repair for hI ,ηi, then there is a branch

of T

hI ,ηi

ending with a leaf labeled by U.

4. If U is a founded repair for hI ,ηi, then there is a

branch of T

hI ,ηi

ending with a leaf labeled by U.

5. If U is a justiﬁed repair for hI ,ηi, then there is a

branch of T

hI ,ηi

ending with a leaf labeled by U.

6. If η is a set of normal AICs and hU, J i is a leaf of

hI ,ηi

with U consistent and U ∩ J =

0, then U is

a justiﬁed repair for hI ,ηi.

Not all leaves will correspond to repairs of the

desired kind; in particular, there may be weak re-

pairs in repair trees. Also, both T

hI ,ηi

and T

hI ,ηi

typi-

cally contain leaves that do not correspond to founded

or justiﬁed (weak) repairs – otherwise the problem

repAIrC: A Tool for Ensuring Data Consistency - By Means of Active Integrity Constraints

of deciding whether there exists a founded or justi-

ﬁed weak repair for hI , ηi would be solvable in non-

deterministic polynomial time. The leaves of the

well-founded repair tree for hI ,ηi correspond to a

new type of weak repairs, called well-founded weak

repairs, not considered in the original works on AICs.

2.3 Parallel Computation of Repairs

The computation of founded or justiﬁed repairs can

be improved by dividing the set of AICs into indepen-

dent sets that can be processed independently, simply

merging the computed repairs at the end (Cruz-Filipe,

2014). Here, we adapt the deﬁnitions given therein

to the ﬁrst-order scenario. Two sets of AICs η

and

are independent if the same atom does not occur

in a literal in the body of a closed instance of two

distinct rules r

∈ η

and r

∈ η

. If η

and η

are

independent, then repairs for hI,η

∪ η

i are exactly

the unions of a repair for hI ,η

i and hI ,η

i; further-

more, the result still holds if one considers founded,

well-founded or justiﬁed repairs.

If an atom occurs in a literal in the body of a closed

instance of a rule in η

and in an action in the head of

a closed instance of a rule in η

, but not conversely,

then we say that η

precedes η

. Founded/justiﬁed

(but not well-founded) repairs for η

∪η

can be com-

puted in a stratiﬁed way, by ﬁrst repairing I w.r.t. η

and then repairing the result w.r.t. η

Splitting a set of AICs into independent sets or

stratifying it can be solved using standard algorithms

on graphs, as we describe in Section 4.

3 THE TOOL

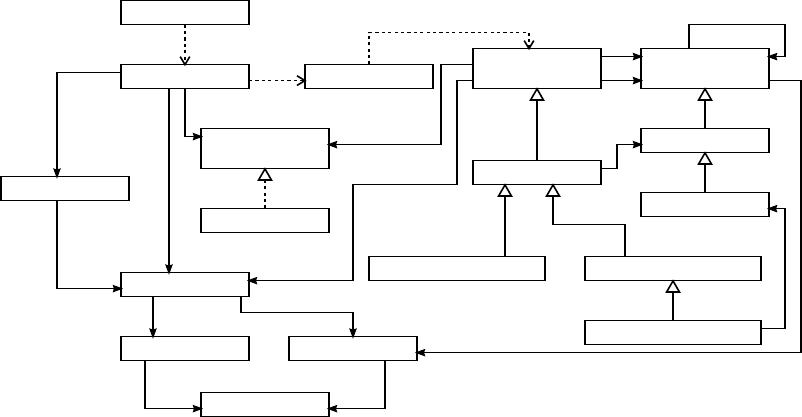
The tool repAIrC is implemented in Java, and its sim-

pliﬁed UML class diagram can be seen in Figure 1.

Structurally, this tool can be split into four main sepa-

rate components, centered on the four classes marked

in bold in that ﬁgure.

• Objects of type AIC implement active integrity

constraints.

• Implementations of interface DB provide the nec-

essary tools to interact with a particular database

management system; currently, we provide func-

tionality for SQL databases supported by JDBC.

• Objects of type RepairTree correspond to con-

crete repair trees; their exact type will be the sub-

class corresponding to a particular kind of repairs.

• Class RunRepairGUI provides the graphical inter-

face to interact with the user.

An important design aspect has to do with ex-

tensibility and modularity. A ﬁrst prototype focused

on the construction of repair trees, and used simple

text ﬁles to mimick databases as lists of propositional

atoms, in the style of (Caroprese and Truszczy

nski,

2011; Cruz-Filipe et al., 2013). Later, parallelization

capabilities were added (as explained in Section 4),

requiring changes only to RepairController – the

class that controls the execution of the whole process.

Likewise, the extension of repAIrC to SQL databases

and the addition of the stratiﬁcation mechanism only

required localized changes in the classes directly con-

cerned with those processes.

The next subsections detail the implementa-

tion of the classes AIC, DB, RepairTree and

RunRepairTreeGUI.

3.1 Representing Active Integrity

Constraints

In the practical setting, it makes sense to diverge a

little from the theoretical deﬁnition of AICs.

• Real-world tables found in DBs contain many

columns, most of which are typically irrelevant

for a given integrity constraint.

• The columns of a table are not static, i.e., columns

are usually added or removed during a database’s

lifecycle.

• The order of columns in a table should not matter,

as they are identiﬁed by a unique column name.

To deal pragmatically with these three aspects, we

will write atoms using a more database-oriented

notation, allowing the arguments to be provided

in any order, but requiring that the column names

be provided. The special token $ is used as ﬁrst

character of a variable. So, for example, the literal

hasInsurance(firstName=$X, type=’basic’)

will match any entry in table hasInsurance having

value basic in column type and any value in column

firstName; this table may additionally have other

columns. Negative literals are preceded by the

keyword NOT, while actions must begin with + or -.

Literals and actions are separated by commas, and the

body and head of an AIC are separated by ->. The

AIC is ﬁnished when ; is encountered, thus allowing

constraints to span several lines.

AICs are provided in a text ﬁle, which is parsed

by a parser generated automatically using JavaCC

and transformed into objects of type AIC. These

contain a body and a head, which are respectively

List<Literal> and List<Action>; for consistency

with the underlying theory, Literal and Action are

implemented separately, although their objects are

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

RepairController

RunRepairGUI

SimpleNode

JustifiedNode

SimpleRepairTree

FoundedRepairTree WellFoundedRepairTree

JustifiedRepairTree

AIC

Literal Action

DBMySQL

abstract

RepairTree

abstract

Node

interface

RepairGUI

create

call *{List}

*{List} *{List}

*{List}

*{Set}

Clause

Preprocess

*{List}

Figure 1: Class diagram for repAIrC.

isomorphic: they contain an object of type Clause

(which consists of the name of a table in the database

and a list of pairs column name/value) and a ﬂag indi-

cating whether they are positive/negated (literals) or

additions/removals (actions).

Example 1. Consider the following active integrity

constraints for an employee database. The ﬁrst states

that the boss (as speciﬁed in the category table) can-

not be a junior employee (i.e., have an entry in the

junior table); the second states that every junior em-

ployee must have some basic insurance (as speciﬁed

in the insured table).

junior(X ),category(boss, X) ⊃ −junior(X)

junior(X ),not insured(X,basic)

⊃ +insured(X,basic)

These are written in the concrete text-based syntax

of the repAIrC tool as

junior(id = $X),

category(type = boss, empId = $X)

-> - junior(id = $X);

junior(id = $X),

NOT insured(empId = $X, type = basic)

-> + insured(empId = $X, type = basic);

respectively, assuming the corresponding column

names for the atributes. Note that, thanks to our usage

of explicit column naming, the column names for the

same variable need not have identical designations.

3.2 Interfacing with the Database

Database operations (queries and updates) are de-

ﬁned in the DB interface, which contains the following

methods.

• getUpdateActions(AIC aic): queries the

database for all the instances of aic that are

not satisﬁed in its current state, returning a

Collection<Collection<Action>> that con-

tains the corresponding instantiations of the head

of aic.

• update(Collection<Action> actions): ap-

plies all update actions in actions to the database

(void).

• undo(Collection<Action> actions): undoes

the effect of all update actions in actions (void).

• aicsCompatible(Collection<AIC> aics):

checks that all the elements of aics are compati-

ble with the structure of the database.

• disconnect(): disconnects from the database

(void). The connection is established when the

object is originally constructed.

Some of these methods require more detailed

comments. The construction of the repair tree also re-

quires that the database be changed interactively, but

upon conclusion the database should be returned to its

original state. In theory, this would be achievable by

applying the update method with the duals of the ac-

tions that were used to change the database; but this

turns out not to be the case for deletion actions. Since

the AICs may underspecify the entries in the database

(because some ﬁelds are left implicit), the implemen-

tation of update must take care to store the values

of all rows that are deleted from the database. In turn,

the undo method will read this information every time

repAIrC: A Tool for Ensuring Data Consistency - By Means of Active Integrity Constraints

it has to undo a deletion action, in order to ﬁnd out ex-

actly what entries to re-add.

The method aicsCompatible is necessary be-

cause the AICs are given independently of the

database, but they must be compatible with its struc-

ture – otherwise, all queries will return errors. Includ-

ing this method in the interface allows the AICs to be

tested before any queries are made, thus signiﬁcantly

reducing the number of exceptions that can occur dur-

ing program execution.

Currently, repAIrC includes an implementation

DBMySQL of DB, which works with SQL databases.

The interaction between repAIrC and the database

is achieved by means of JDBC, a Java database con-

nectivity technology able to interface with nearly

all existing SQL databases. In order to determine

whether an AIC is satisﬁed by a database, method

getUpdateActions ﬁrst builds a single SQL query

corresponding to the body of the AIC. This method

builds two separate SELECT statements, one for the

positive and another for the negative literals in the

body of the AIC. Each time a new variable is found,

the table and column where it occurs are stored, so

that future references to the same variable in a positive

literal can be uniﬁed by using inner joins. The select

statement for the negative literals is then connected to

the other one using a WHERE NOT EXISTS condition.

Variables in the negative literals must necessarily ap-

pear ﬁrst in a positive literal in the same AIC; there-

fore, they can then be connected by a WHERE clause

instead of an inner join.

Example 2. The bodies of the integrity constraints in

Example 1 generate the following SQL queries.

SELECT * FROM junior

INNER JOIN dept_emp

ON junior.id=category.empId

WHERE category.type=‘boss’

SELECT * FROM junior

WHERE NOT EXISTS

(SELECT * FROM insured

WHERE insured.empId=junior.id

AND insured.type=‘basic’)

3.3 Implementing Repair Trees

The implementation of the repair trees directly fol-

lows the algorithms described in Section 2. Differ-

ent types of repair trees are implemented using inher-

itance, so that most of the code can be reused in the

more complex trees. The trees are constructed in a

breadth-ﬁrst manner, and all non-contradictory leaves

that are found are stored in a list. At the end, this list

is pruned so that only the minimal elements (w.r.t. set

inclusion) remain – as these are the ones that corre-

spond to repairs.

While constructing the tree, the database has to be

temporarily updated and restored. Indeed, to calculate

the descendants of a node, we ﬁrst need to evaluate all

AICs at that node in order to determine which ones are

violated; this requires querying a modiﬁed version of

the database that takes into account the update actions

in the current node.

In order to avoid concurrency issues, these up-

dates are performed in a transaction-style way, where

we update the database, perform the necessary SQL

queries, and rollback to the original state, guarantee-

ing that other threads interacting with the database

during this process neither see the modiﬁcations nor

lead to inconsistent repair trees. This becomes of

particular interest when the parallel processing tools

described in Section 4 are put into place. Although

this adds some overhead to the execution time, at the

end of that section we discuss why scalability is not a

practically relevant concern.

After ﬁnding all the leaves of the repair tree, a

further step is needed in the case one is looking for

founded or justiﬁed repairs, as the corresponding trees

may contain leaves that do not correspond to repairs

with the desired property. This step is skipped if all

AICs are normal, in view of the results from (Cruz-

Filipe et al., 2013). For founded repairs, we directly

apply the deﬁnition: for each action α, check that

there is an AIC with α in its head and such that all

other literals in its body are satisﬁed by the database.

For justiﬁed repairs, the validation step is less ob-

vious. Directly following the deﬁnition requires con-

structing the set of no-effect actions, which is essen-

tially as large as the database, and iterating over sub-

sets of this set. This is obviously not possible to do in

practical settings. Therefore, we use some criteria to

simplify this step.

Lemma 1. If a rule r was not applied in the branch

leading to U, then U is closed under r.

Proof. Suppose that r was never applied and assume

nup(r) ⊆ ne(I ,I ◦ U). Then necessarily head (r) ∩

ne(I ,I ◦ U) 6=

0, otherwise r would be applicable and

U would not be a repair.

By construction, U is also closed for all rules ap-

plied in the branch leading to it.

Let U be a candidate justiﬁed weak repair. In or-

der to test it, we need to show that U ∪ ne(I , I ◦ U)

is a justiﬁed action set (see (Cruz-Filipe et al., 2013)),

which requires iterating over all subsets of U ∪

ne(I ,I ◦ U) that contain ne (I ,I ◦ U). Clearly this

can be achieved by iterating over subsets of U.

But if U

∗

⊆ U, then nup(r) ∩ U

∗

0; this al-

lows us to simplify the closedness condition to: if

nup(r) ⊆ ne(I ,I ◦ U), then U

∗

∩ head (r) =

0. The

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

antecedent needs then only be done once (since it only

depends on U), whereas the consequent does not re-

quire consulting the database.

The following result summarizes these properties.

Lemma 2. A weak repair U in a leaf of the justi-

ﬁed repair tree for hI ,ηi is a justiﬁed weak repair

for hI ,ηi iff, for every set U

∗

⊆ U, if nup(r) ⊆

ne(I ,I ◦ U), then U

∗

∩ head(r) =

The different implementations of repair trees use

different subclasses of the abstract class Node; in par-

ticular, nodes of JustifiedRepairTrees must keep

track not only of the sets of update actions being con-

structed, but also of the sets of non-updatable ac-

tions that were assumed. These labels are stored as

Set<Action> using HashSet from the Java library

as implementation, as they are repeatedly tested for

membership everytime a new node is generated.

For efﬁciency, repair trees maintain internally a

set of the sets of update actions that label nodes con-

structed so far as a Set<Node>. This is used to avoid

generating duplicate nodes with the same label. Since

this set is used mainly for querying, it is again imple-

mented as a HashSet. Nodes with inconsistent labels

are also immediately eliminated, since they can only

produce inconsistent leaves.

3.4 Interfacing with the User

The user interface for repAIrC is implemented us-

ing the standard Java GUI widget toolkit Swing, and

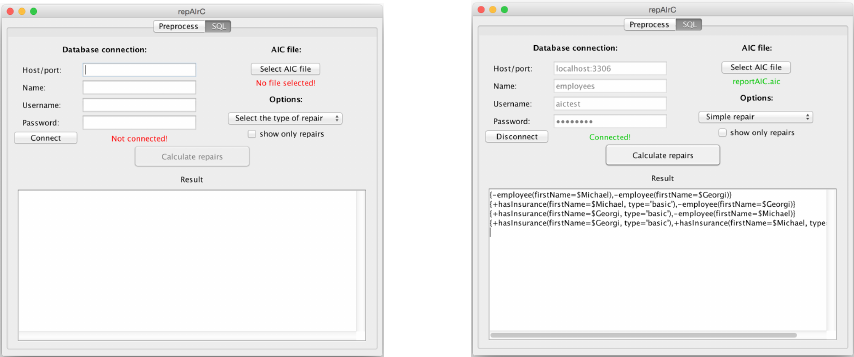
is rather straightforward. On startup, the user is pre-

sented with the dialog box depicted in Figure 2.

The user can then provide credentials to connect

to a database, as well as enter a ﬁle containing a set

of AICs. If the connection to the database is success-

ful and the ﬁle is successfully parsed, repAIrC in-

vokes the aicsCompatible method required by the

Figure 2: The initial screen for repAIrC.

implementation of the DB interface (see Section 3.2)

and veriﬁes that all tables and columns mentioned in

the set of AICs are valid tables and columns in the

database. If this is not the case, then an error mes-

sage is generated and the user is required to select

new ﬁles; otherwise, the buttons for conﬁguration and

computation of repairs become active.

Once the initialization has succeeded, one can

check the database for consistency and obtain differ-

ent types of repairs, computed using the repair tree

described above. As it may be of interest to obtain

also weak repairs, the user is given the possibility of

selecting whether to see only the repairs computed,

or all valid leaves of the repair tree – which typically

include some weak repairs. In both cases the neces-

sary validations are performed, so that leaves that do

not correspond to repairs (in the case of founded or

justiﬁed repairs) are never presented.

An example output screen after successful compu-

tation of the repairs for an inconsistent database can

be seen in Figure 3.

4 PARALLELIZATION AND

STRATIFICATION

As described in Section 2.3, it is possible to paral-

lelize the search for repairs of different kinds by split-

ting the set of AICs into independent sets; in the case

of founded or justiﬁed repairs, this parallelization can

be taken one step further by also stratifying the set

of AICs. Even though ﬁnding partitions and/or strat-

iﬁcations is asymptotically not very expensive (it can

be solved in linear time by the well-known graph al-

gorithms described below), it may still take noticeable

time if the set of AICs grows very large.

Since, by deﬁnition, partitions and stratiﬁcations

Figure 3: Possible repairs of an inconsistent database.

repAIrC: A Tool for Ensuring Data Consistency - By Means of Active Integrity Constraints

are independent of the actual database, it makes sense

to avoid repeating their computation unless the set of

AICs changes. For this reason, parallelization capa-

bilities are implemented in repAIrC in a two-stage

process. Inside repAIrC, the user can switch to the

Preprocess tab, which provides options for comput-

ing partitions and stratiﬁcations of a set of AICs. This

results in an annotated ﬁle which still can be read by

the parser; in the main tab, parallel computation is

automatically enabled whenever the input ﬁle is an-

notated in a proper manner.

4.1 Implementation

Computing optimal partitions in the spirit of (Cruz-

Filipe, 2014) is not feasible in a setting where vari-

ables are present, as this would require considering

all closed instances of all AICs – but it is also not de-

sirable, as it would also result in a signiﬁcant increase

of the number of queries to the database. Instead, we

work with the adapted deﬁnition of dependency given

in Section 2. Given a set of AICs, repAIrC constructs

the adjacency matrix for the undirected graph whose

nodes are AICs and such that there is an edge between

to r

iff r

and r

are not independent. A partition is

then computed simply by ﬁnding the connected com-

ponents in this graph by a standard graph algorithm.

The partitions computed are then written to a ﬁle,

where each partition begins with the line

#PARTITION_BEGIN_[NO]#

where [NO] is the number of the current partition, and

ends with

#PARTITION_END#

and the AICs in each partition are inserted in between,

in the standard format.

To compute the partitions for stratiﬁcation, we

need to ﬁnd the strongly connected components of a

similar graph. This is now a directed graph where

there is an edge from r

to r

if r

precedes r

. The im-

plementation is a variant of Tarjan’s algorithm (Tar-

jan, 1972), adapted to give also the dependencies be-

tween the connected components.

The computed stratiﬁcation is then written to a ﬁle

with a similar syntax to the previous one, to which

a dependency section is added, between the special

delimiters

#DEPENDENCIES_BEGIN#

and

#DEPENDENCIES_END#

The dependencies are included in this section as a se-

quence of strings X -> Y, one per line, where X and Y

are the numbers of two partitions and Y precedes X.

Example 3. The two AICs from Example 1 cannot

be parallelized, as they both use the junior table,

but they can be stratiﬁed, as only the ﬁrst one makes

changes to this table. Preprocessing this example by

repAIrC would return the following output.

#PARTITION_BEGIN_1#

junior(id = $X),

category(type = boss, empId = $X)

-> - junior(id = $X);

#PARTITION_END#

#PARTITION_BEGIN_2#

junior(id = $X),

NOT insured(empId = $X, type = basic)

-> + insured(empId = $X, type = basic);

#PARTITION_END#

#DEPENDENCIES_BEGIN#

2 -> 1

#DEPENDENCIES_END#

Imagine a simple scenario where the junior ta-

ble contains a single entry. Then, computing repairs

for this set of AICs can be achieved by ﬁrst repair-

ing partition 1 (which will generate a tree with only

one node) and then repairing the resulting database

w.r.t. partition 2 (which builds another tree, also with

only one node). By comparison, processing the two

AICs simultaneously would potentially give a tree

with 4 nodes, as both AICs would have to be consid-

ered at each stage.

In general, if there are n entries in the junior ta-

ble, the stratiﬁed approach will construct at most n+1

trees with a total of n

+ n nodes (one tree with n

nodes for the ﬁrst AIC, at most n trees with at most

n nodes for the second AIC). By contrast, process-

ing both AICs together will construct a tree with po-

tentially (2n)! leaves, which by removing duplicate

nodes may still contain 2

nodes.

This example shows that, by stratifying AICs, we

can actually get an exponential decrease on the size of

the repair trees being built – and therefore also on the

total runtime.

In addition to alleviating the exponential blowup

of the repair trees, parallelization and stratiﬁca-

tion also allow for a multi-threaded implementation,

where repair trees are built in parallel in multiple con-

current threads. To ensure that the dependencies be-

tween the partitions are respected, the threads are in-

structed to wait for other threads that compute pre-

ceding partitions. In Example 3, the thread process-

ing partition 2 would be instructed to ﬁrst wait for the

thread processing partition 1 to ﬁnish.

Our empirical evaluation of repAIrC showed that

speedups of a factor of 4 to 7 were observable even

when processing small parallelizable sets of only two

or three AICs. For larger sets of AICs, paralleliza-

tion and stratiﬁcation are necessary to obtain feasi-

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

ble runtimes. In one application, which allowed for

15 partitions to be processed independently, the strat-

iﬁed version computed the founded repairs in approx-

imately 1 second, whereas the sequential version did

not terminate within a time limit of 15000 seconds.

This corresponds to a speedup of at least four orders

of magnitude, demonstrating the practical impact of

the contributions of this section.

4.2 Practical Assessment

In the worst case, parallelization and stratiﬁcation will

have no impact on the construction of the repair tree,

as it is possible to construct a set of AICs with no

independent subsets. However, the worst case is not

the general case, and it is reasonable to believe that

real-life sets of AICs will actually have a high paral-

lelization potential.

Indeed, integrity constraints typically reﬂect high-

level consistency requirements of the database, which

in turn capture the hierarchical nature of relational

databases, where more complex relations are built

from simpler ones. Thus, when specifying active in-

tegrity constraints there will naturally be a preference

to correct inconsistencies by updating the more com-

plex tables rather than the most primitive ones.

Furthermore, in a real setting we are not so much

interested in repairing a database once, but rather in

ensuring that it remains consistent as its information

changes. Therefore, it is likely that inconsistencies

that arise will be localized to a particular table. The

ability to process independent sets of AICs separately

guarantees that we will not be repeatedly evaluat-

ing those constraints that were not broken by recent

changes, focusing only on the constraints that can ac-

tually become unsatisﬁed as we attempt to ﬁx the in-

consistency.

For the same reason, scalability of the techniques

we implemented is not a relevant issue: there is no

practical need to develop a tool that is able to ﬁx hun-

dreds of inconsistencies efﬁciently simultaneously,

since each change to the database will likely only im-

pact a few AICs.

5 CONCLUSIONS AND FUTURE

WORK

We presented a working prototype of a tool, called

repAIrC, to check integrity of real-world SQL

databases with respect to a given set of active in-

tegrity constraints, and to compute different types

of repairs automatically in case inconsistency is de-

tected, following the ideas and algorithms in (Flesca

et al., 2004; Caroprese et al., 2007; Caroprese and

Truszczy

nski, 2011; Cruz-Filipe et al., 2013; Cruz-

Filipe, 2014). This tool is the ﬁrst implementation of

a concept we believe to have the potential to be inte-

grated in current database management systems.

Our tool currently does not automatically apply

repairs to the database, rather presenting them to the

user. As discussed in (Eiter and Gottlob, 1992), such

a functionality is not likely to be obtainable, as human

intervention in the process of database repair is gener-

ally accepted to be necessary. That said, automating

the generation of a small and relevant set of repairs

is a ﬁrst important step in ensuring a consistent data

basis in Knowledge Management.

In order to deal with real-world heterogenous

knowledge management systems, we are currently

working on extending and generalizing the notion of

(active) integrity constraints to encompass more com-

plex knowledge repositories such as ontologies, ex-

pert reasoning systems, and distributed knowledge

bases. The design of repAIrC has been with this ex-

tension in mind, and we believe that its modularity

will allow us to generalize it to work with such knowl-

edge management systems once the right theoretical

framework is developed.

On the technical side, we are planning to speed up

the system by integrating a local database cache for

peforming the many update and undo actions during

exploration of the repair trees without the overhead of

an external database connection.

ACKNOWLEDGMENTS

This work was supported by the Danish Council

for Independent Research, Natural Sciences, and by

FCT/MCTES/PIDDAC under centre grant to BioISI

(Centre Reference: UID/MULTI/04046/2013). Marta

Ludovico was sponsored by a grant “Bolsa Universi-

dade de Lisboa / Fundac¸

ao Amadeu Dias”.

REFERENCES

Abiteboul, S. (1988). Updates, a new frontier. In Gyssens,

M., Paredaens, J., and van Gucht, D., editors,

ICDT’88, 2nd International Conference on Database

Theory, Bruges, Belgium, August 31 – September 2,

1988, Proceedings, volume 326 of LNCS, pages 1–18.

Springer.

Caroprese, L., Greco, S., and Molinaro, C. (2007). Priori-

tized active integrity constraints for database mainte-

nance. In Ramamohanarao, K., Krishna, P. R., Mo-

hania, M. K., and Nantajeewarawat, E., editors, Ad-

vances in Databases: Concepts, Systems and Appli-

repAIrC: A Tool for Ensuring Data Consistency - By Means of Active Integrity Constraints

cations, 12th International Conference on Database

Systems for Advanced Applications, DASFAA 2007,

Bangkok, Thailand, April 9-12, 2007, Proceedings,

volume 4443 of LNCS, pages 459–471. Springer.

Caroprese, L., Greco, S., and Zumpano, E. (2009). Active

integrity constraints for database consistency mainte-

nance. IEEE Transactions on Knowledge and Data

Engineering, 21(7):1042–1058.

Caroprese, L. and Truszczy

nski, M. (2011). Active integrity

constraints and revision programming. Theory and

Practice of Logic Programming, 11(6):905–952.

Cruz-Filipe, L. (2014). Optimizing computation of repairs

from active integrity constraints. In Beierle, C. and

Meghini, C., editors, Foundations of Information and

Knowledge Systems - 8th International Symposium,

FoIKS 2014, Bordeaux, France, March 3-7, 2014.

Proceedings, volume 8367 of LNCS, pages 361–380.

Springer.

Cruz-Filipe, L., Engr

acia, P., Gaspar, G., and Nunes, I.

(2013). Computing repairs from active integrity con-

straints. In Wang, H. and Banach, R., editors, 2013 In-

ternational Symposium on Theoretical Aspects of Soft-

ware Engineering, Birmingham, UK, July 1st–July 3rd

2013, pages 183–190. IEEE.

Duhon, B. R. (1998). It’s all in our heads. Informatiktage,

12(8):8–13.

Eiter, T. and Gottlob, G. (1992). On the complexity of

propositional knowledge base revision, updates, and

counterfactuals. Artiﬁcial Intelligence, 57(2–3):227–

270.

Flesca, S., Greco, S., and Zumpano, E. (2004). Active

integrity constraints. In Moggi, E. and Scott War-

ren, D., editors, Proceedings of the 6th International

ACM SIGPLAN Conference on Principles and Prac-

tice of Declarative Programming, 24–26 August 2004,

Verona, Italy, pages 98–107. ACM.

Katsuno, H. and Mendelzon, A. O. (1991). On the differ-

ence between updating a knowledge base and revising

it. In Allen, J. F., Fikes, R., and Sandewall, E., edi-

tors, Proceedings of the 2nd International Conference

on Principles of Knowledge Representation and Rea-

soning (KR’91). Cambridge, MA, USA, April 22-25,

1991, pages 387–394. Morgan Kaufmann.

onig, M. E. (2012). What is KM? Knowledge Manage-

ment Explained, http://www.kmworld.com/.

Tarjan, R. E. (1972). Depth-ﬁrst search and linear graph

algorithms. SIAM Journal on Computing, 1(2):146–

160.

Winslett, M. (1990). Updating Logical Databases. Cam-

bridge Tracts in Theoretical Computer Science. Cam-

bridge University Press.

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing