Interval Type 2- Fuzzy Rule based System Approach for Selection

of Alternatives using TOPSIS

Abdul Malek Yaakob

1,2

, Ku M. Naim Ku Khalif

Alexander Gegov

and Siti Fatimah Abdul Rahman

School of Quantitative Science, Universiti Utara Malaysia, 06010 Sintok, Kedah, Malaysia

School of Computing, Buckingham Building, University of Portsmouth, Portsmouth, PO1 3HE, U.K.

Department of Mathematics & Statistics, Universiti Teknologi MARA(Perlis), 02600 Arau, Perlis, Malaysia

Keywords: Fuzzy Decision Making, Ranking Alternative, TOPSIS, Type 2 Fuzzy Set, Fuzzy Rule based System,

Influence Degree, Stock Selection, and Assessing Ranking Performance.

Abstract: The paper considers fuzzy rule based system for multi criteria group decision making problem. A novel

version of TOPSIS method using interval type 2 fuzzy rule based system approach is proposed with the

objective of improving the type 2 TOPSIS ability to deal with ambiguity through the combination of the

mathematical process involved in the type 2 TOPSIS with the expert empirical knowledge. On the other

hand, a hybrid analysis of decision making process that requires the use of human sensitivity to reflect

influence degree of decision maker can be expressed by a fuzzy rule base. To ensure practicality and

effectiveness of proposed method, stock selection problem is studied. The ranking based on proposed

method is validated comparatively using Kendall’s Tau rank correlation. Based on the result, the proposed

method outperforms the established non-rule based version of type 2 TOPSIS in term of ranking

performance.

1 INTRODUCTION

Multi criteria decision making has received great

attention recently in optimization problems

(Shidpour et al. 2013)(Awasthi et al. 2011) and

(Şengül et al. 2015). This is due to the fact that the

ability of decision makers in providing result that is

consistent with actual situation remains as major

concern in decision making environment.

Conventional Technique for Order of Preference by

Similarity to Ideal Solution (TOPSIS) was

originally developed in (Hwang, C.L.Yoon 1981).

Later, the conventional to T1 TOPSIS was enhanced

to provide additional flexibility in represent the

uncertainty (Chen 2000). A decade later, a fuzzy

rule based version of T1-TOPSIS was develop,

which provide a basis for automatic generation of a

rule base to assist the analysis of decision making

problem (Santos and Camargo 2010).

In 2010, a TOPSIS method based on interval

Type 2 (T2) fuzzy set was introduced which

demonstrate additional degree of freedom to

represent the uncertainty and the fuzziness of the

real world problems. In order to improve the ability

in dealing and presenting vagueness of information

in established non rule based T2 TOPSIS

method(Chen and Lee 2010), T2 - Fuzzy Rule Based

TOPSIS (T2 FRBS TOPSIS) is introduce in this

paper, which has capability in providing a useful

way to handle MCDM problems in a more flexible

and intelligent manner but also presenting expert’s

knowledge accurately and significantly.

The paper is organized as follows. Section 2

briefly reviews the concept of interval T2 fuzzy set.

The proposed method is systematically explained in

section 3. In section 4, stock selection problem is

explained using the proposed method. Next, ranking

performance is assessed and analysis of result is

discussed in section 5. Finally, the conclusion is

drawn.

2 BASIC CONCEPT

In the following, we briefly review some basic

definitions of fuzzy sets from (Chen, 2000) and

(Chen and Lee 2010). These basic definitions and

112

Yaakob, A., Khalif, K., Gegov, A. and Rahman, S..

Interval Type 2- Fuzzy Rule based System Approach for Selection of Alternatives using TOPSIS.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 2: FCTA, pages 112-120

ISBN: 978-989-758-157-1

notations are used throughout the paper unless stated

otherwise.

Definition 1: Fuzzy set

A fuzzy set

is defined on a universe

may

be given as:

()

}|),{(

XxxxA

∈=

Where

()

]1,0[:

→Xx

is the membership

function

. The membership value

()

describes

the degree of belongingness of

Xx ∈

Throughout this paper, type-1 fuzzy number, and

type-2 fuzzy number are presented in the form of

trapezoidal fuzzy number. It is easy to deal with

because it is piece wise linear. On the other hand,

the good coverage of trapezoidal fuzzy number is a

good compromise between efficiency and

effectiveness.

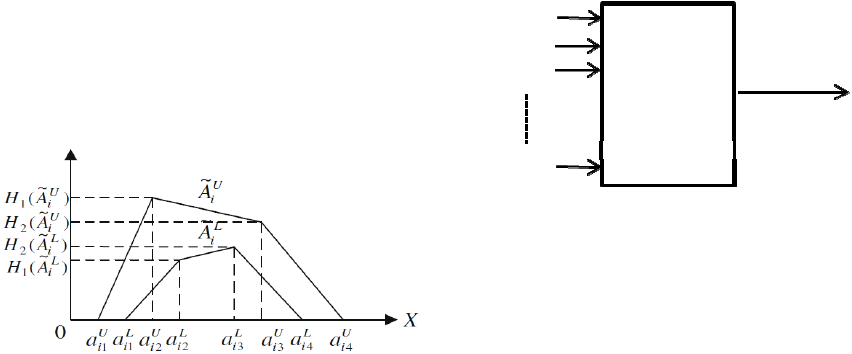
Definition 2: Type-2 Fuzzy Number

A trapezoidal interval type-2 fuzzy set

can be

represented by

()

() ()()













AHAHaaaa

AAA

;,,,

214321

as shown in Figure 1, where

and

are type-1

fuzzy sets,

aaaaaaa

3214321

,,,,,,

and

are

the reference points of the interval type-2 fuzzy set

)

iji

AHA denotes the membership value of the

element

)1( +

in the upper trapezoidal membership

function

)

(,21,

AHjA ≤≤

denotes the membership

value of the lower trapezoidal membership function

,21,

≤≤ jA

and

ni ≤≤1

],1,0[)(],1,0[)(],1,0[)(],1,0[)(

2121

∈∈∈∈

AHAHAHAH

Figure 1: Type-2 Fuzzy Number (Chen and Lee 2010).

3 PROPOSED METHOD

In this section, the authors extend the T2-TOPSIS

method from (Chen and Lee 2010) using fuzzy rule

based approach for handling multi criteria decision

making problem. The main purpose of modification

is to extend the ability of fuzzy rules based approach

into established method. Thus, the implementation

by proposed method allow the empirical knowledge

of the expert, represented by fuzzy rule, also be

considered in the decision making process.

The use of the methods associated with the empirical

knowledge of experts, allows a hybrid analysis of

the decision making problems where the process of

decision making requires the use of human

sensitivity, which often can be expressed by a fuzzy

rules base. Thus, the behavior of the system may

have greater influence then the rule defined by the

decision maker. The authors adopt the methods

described in (Santos and Camargo 2010) for the

knowledge of the influence degree of each decision

maker.

In case in which one decision maker has more

knowledge of the domain, optionally the opinion of

this expert may have greater degree of importance

than the other decision makers in the analysis of the

problem. Thus, the proposed method can identify

and aggregate the different opinions of decision

makers with varying influence degrees to suggest the

final solution. Figure 2 schematically

demonstrations such a system, where C

, C

…

is the input, in this case criteria and Y represents

the output/ alternative level. The rules for such a

system are normally derived from expert knowledge.

Figure 2: Fuzzy System.

Just as in established fuzzy TOPSIS method, Table 1

and Table 2 are used to represent the importance of

criteria and the rating of the alternative. In order to

deal with influence degree of decision maker in T2

fuzzy rule based approach, Table 3 introduce here,

which implement the consequent part of the rules.

The linguistic terms that represents the consequents

of rules was named “Alternative Level” and is

represented by fuzzy sets “Very bad”, “Bad”,

“Regular”, “Good” and “Excellent”.

Rule Base

Interval Type 2- Fuzzy Rule based System Approach for Selection of Alternatives using TOPSIS

113

Table 1: Linguistic terms for the importance weight of

each criterion.

Linguistic Type 2 Fuzzy Number

Very Low (VL) (0.00,0.00,0.00,0.10,1,1)(0.00,0.00,0.00,0.10,1,1)

Low (L) (0.00,0.10,0.10,0.25,1,1)(0.00,0.10,0.10,0.25,1,1)

Medium Low (ML) (0.15,0.30,0.30,0.45,1,1)(0.15,0.30,0.30,0.45,1,1)

Medium (M) (0.35,0.50,0.50,0.65,1,1)(0.35,0.50,0.50,0.65,1,1)

Medium High (MH) (0.55,0.70,0.70,0.85,1,1)(0.55,0.70,0.70,0.85,1,1)

High (H) (0.80,0.90,0.90,1.00,1,1)(0.80,0.90,0.90,1.00,1,1)

Very High (VH) (0.90,1.00,1.00,1.00,1,1)(0.90,1.00,1.00,1.00,1,1)

Table 2: Linguistic terms for rating of all alternative.

Linguistic Trapezoidal Fuzzy Number

Very Poor (VP) (0,0,0, 1,1) (0,0,0, 1,1)

Poor (P) (0,1,1,3,1,1) (0,1,1,3,1,1)

Medium Poor (MP) (1,3,3,5,1,1) (1,3,3,5,1,1)

Fair (F) (3,5,5,7,1,1) (3,5,5,7,1,1)

Medium Good (MG) (5,7,7,9,1,1) (5,7,7,9,1,1)

Good (G) (7,9,9,10,1,1) (7,9,9,10,1,1)

Very Good (VG) (9,10,10,10,1,1)(9,10,10,10,1,1)

Table 3: Linguistic term for alternative level.

Linguistic Trapezoidal Fuzzy Number

Very Bad(VB) (0.00,0.00,0.00,0.25,1,1)(0.00,0.00,0.00,0.25,1,1)

Bad (B) (0.00,0.25,0.25,0.50,1,1)(0.00,0.25,0.25,0.50,1,1)

Regular (R) (0.25,0.50,0.50,0.75,1,1)(0.25,0.50,0.50,0.75,1,1)

Good (G) (0.50,0.75,0.75,1,1,1) (0.50, 0.75, 0.75, 1,1,1)

Very Good (VG) (0.75,1.00,1.00,1.00,1,1) (0.75,1.00,1.00,1.00,1,1)

The following algorithm is conducted to get the

ranking of alternatives, whereby Step 1-5 are taken

from (Chen & Lee 2010), whereas Step 6 to Step 8

are introduced in this paper.

T2- FRBS TOPSIS algorithm

Instead of calculating the average decision

matrix as the previous TOPSIS methods(Mohamad

and Jamil 2012),(Kelemenis et al. 2011). Here, the

opinion of each decision maker evaluated

independently. Assume that there are

alternatives

AAA ,,,



and assume that there are

criteria

121

,,,,

+nn

CCCC 

. Where

1+n

represent the

influence level of each decision maker. Let there are

decision makers

DMDMDM ,,,

 then will

have

decision matrix.

Step 1: Construct Fuzzy Decision Matrix,

()

and Fuzzy Weight of Alternative

()

W as shown in

Eq. (1).

()













mnmm

xxx







22221

11211

and

[]

wwwW 

(1)

where

and

are interval T2 fuzzy set based

from Table 1 and Table 2 respectively. Its represent

the rating and the important weights of the

decision maker of alternative

A with respect to

criterion

()

nj ,,1 =

respectively.

Step 2: Weighted fuzzy decision matrix

()

The weighted fuzzy decision matrix

()

V is shown

in Eq. (2).

[

]

ijK

for

mi ,,1 =

and

nj ,,1 =

(2)

where

()

ijijij

wxv ⋅=

is an multiplication of interval

T2 fuzzy set.

Step 3: Construct the ranking weighted decision

matrix

Calculate the ranking value

)(

ARank (Lee and

Chen 2008), in order to find ranking value, the

maximum number

of edges in the upper

membership function

and the lower membership

function

of interval T2 fuzzy set

v are defined,

where

ni ≤≤1

and

mj ≤≤1

. If

is odd number

and

3≥s

, then

1+= sr

. If

is even number

and

4≥s

, then

. The )(

ARank of interval T2

fuzzy set is shown in Eq. (3).

()

(

)

(

)

() () ()





∈

−

∈∈

∈∈∈

∈

−

∈∈

++++













+++−

+++=

},{

},{},{

},{

LUj

iii

AHAHAH

ASASAS

AMAMAMARank



(3)

where

(

)

AM denotes the average of the elements

and

()

for

11 −≤≤ rp

()















−=

aaAS

for

11 −≤≤ rp

The

(

)

denotes the standard deviation of the

elements

aaa ,,,



()















−=

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

114

The

(

)

AH denotes the membership value of the

element

()

21 −≤≤ rp

, },{ LUj ∈ and

even number.

Step 4: The fuzzy positive ideal solution

(

)

and

the fuzzy negative ideal solution

(

)

−

as shown in

Eq. (4).

(

)

++++

vvvA ,,,



and

(

)

−−−−

vvvA ,,,



(4)

where

(

)

{

}

(){}











∈

≤≤

CxvRank

BxvRank

iij

,min

,max

and

(

)

{

}

(){}











∈

≤≤

−

CxvRank

BxvRank

iij

,max

,min

where

denotes the set of benefit attribute and

denotes the set of cost attribute and

ni ≤≤1

To calculate the distance

)(

between each

alternative

A and the fuzzy positive ideal solution

A is shown in Eq. (5).

()



−=

iiji

vvRankAd

)( for

nj ≤≤1

(5)

Calculate the distance

)(

−

between each

alternative

A and the fuzzy negative ideal

solution

−

, as shown in Eq. (6).

()



−−

−=

iiji

vvRankAd

)(

for

nj ≤≤1

(6)

Step 5: The closeness coefficient

()

Calculate the relative degree of closeness

()

CC of

A calculated as shown in Eq. (7)

−+

−

for

mi ,,1 =

(7)

Step 6: The influence Closeness coefficient of each

alternative

The influence degree of each decision maker has

been defined at this point, noting that experts with

more experience have a greater degree of influence

than the expert with less experience.

Let



for

mi ,,1 =

(8)

Where

represent normalized influence degree

for

decision maker.

is the importance degree

between

( unimportant) and 10 (very importance)

of decision maker. Then

iKi

CCICC *

(9)

And it is necessary to normalize the

ICC

()

NICC

to ensure that the

ICC value varies between 0 to 1.

ICC

NICC

max

(10)

Step 7: The matrix of antecedent

()

Λ and the matrix

of consequent

()

A matrix of antecedents is defined as in Eq. (11)













=Λ

mnmm

XXX







22221

11211

(11)

where

is a linguistic terms representing decision

maker opinion of each alternative with respect to the

criteria.

Once

NICC for each alternative defined by each

decision maker is obtained, it is used to determine

the consequents of alternative rules according to the

fuzzy set with higher membership in Table 3. Then a

matrix of consequents is define in Eq. (12)















(12)

where

is a linguistic terms based on Table 3

representing the output of the system based on Eq.

(10) to find the value of

NICC .

Interval Type 2- Fuzzy Rule based System Approach for Selection of Alternatives using TOPSIS

115

Hence, matrix of antecedent and matrix of

consequent in Eq. (11) and (12) can be written as If-

then rule as follow:

If C

is X

and C

is X

and ... and C

is X

then A

is Y

If C

is X

and C

is X

and ... and C

is X

then A

is Y

  

If C

is X

and C

is X

and ... and C

is X

then

is Y

Step 8: The final score

()

for each alternative is

given as shown in Eq. (13).

Ω=

(13)

where

is a crisp value of aggregate membership

function of the output in Eq. (12) defined as shown

in Eq. (14)



αλ

(14)

where

jij

Y∈

is maximum membership degree of

the output. In order to obtain a better representation

in the ranking made by T2- FRBS TOPSIS, It is

importance to have influence multiplier when the

alternatives have same ranking position. This show

exactly how each alternative is different even a

small difference. The following general formula to

calculate influence multiplier

()

Ω uses a marginal

closeness coefficient that has maximum membership

degree as shown in Eq. (15).

KNICC



=Ω

(15)

Therefore, from the value of

, the ranking order of

all alternatives can be determined. The best

alternative has higher value of

4 IMPLEMENTATION OF

METHOD

In this case study a Stock selection problem is

considered in which the evaluation was done by

three decision makers. These financial experts

included finance lecturer (DM1), fund manager

(DM2) and PhD finance student (DM3). They

evaluated 25 stocks (S1-S25) listed on Main Board

in Kuala Lumpur Stock Exchange (KLSE) and then

make investment recommendations according to

financial ratio considered.

The most importance ratio considered in

investment is Market Value of Firm (C1) defined as

Market value of firm-to-earnings before

amortization, interest and taxes ratio. This ratio is

one of the most frequently used financial indicators

and the lower this ratio is better. Return on Equity

(C2) used to examine how much the company earns

on the investment of its shareholders. Portfolio

managers examine ROE very carefully and used it

when deciding whether to buy or sell. The higher the

ratio is better. ROE is usually measured as net

income divide by stockholder. Dept/equity ratio

(C3), this ratio belongs to long term solvency ratios

that are intended to address the firm’s long run

ability to meet its obligations. So, it is assume by

DMs that the lower the ratio the better. Current ratio

(C4) is one of the ways to measure liquidity of

company. It explains the ability of a business to

meet its current obligations when fall due. Higher

the ratio is better. Market value/net sales(C5) is

market value ratios of particular interest to the

investor are earnings per common share, the price-

to-earnings ratio, market value-to book value ratio,

earning-to-price ratio. The lower the ratio is the

better. Price/earnings ratio (C6) measure the ratio of

market price of each share of common stock to the

earnings per share, the lower this ratio is better.

In the case study, the alternative of decision

makers to be rank and to be weighted according to

the above mention ratios are 25 stocks listed in

KLSE .In this study, Microsoft Excel was used to

calculate all the calculation involved in the

evaluating the ranking of stocks and the weight of

each criterion. The DMs use the linguistic weighting

terms in Table 1 to assess the importance of the

criteria, and make use information in Table 2 to give

rating for each alternative. All linguistic terms can

be expressed as type 2 trapezoidal fuzzy numbers as

shown in Table 1, 2 and 3. The T2- FRBS TOPSIS

algorithm introduced in Section 3 is now illustrated

for the case study of stock selection problem.

Step 1: Based on information given by experts

and applying Eq. (1), the decision matrix for each

alternative can be constructed.

The important of criteria and the rating of each are

obtained from questionnaire.

Step 2: Construct a Weighted Decision

Matrix

()

Based on Eq. (2), the normalized weighted decision

matrices can be determined, shown as follows:

()()

0.1,0.1,0.1,0.1,0.1,9.00.1,0.1,0.1,0.1,0.1,9.0

()()

0.1,0.1,10,10,10,90.1,0.1,10,10,10,9

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

116

Then

()()()()()

0.1,0.1,100.1,100.1,100.1,99.0

××××=v

()()()()()

0.1,0.1,100.1,100.1,100.1,99.0 ××××

()()

0.1,0.1,10,10,10,1.80.1,0.1,10,10,10,1.8

Using formula stated to construct the normalized

fuzzy decision matrix.

The

10max

()()

0.1,0.1,0.1,0.1,0.1,81.00.1,0.1,0.1,0.1,0.1,81.0

0.1,0.1,

1.8

0.1,0.1,

1.8

























The normalization method is to preserve the

property that the ranges of normalized trapezoidal

fuzzy number belong to

[]

1,0

Step 3: Construct the ranking weighted decision

matrix

Based on Eq.(3) the ranking values

)(

ARank of

the trapezoidal type 2 fuzzy number

v can be

calculated, illustrate for S1 as follows

()

(

)

(

)

(

)

(

)

(

)

()

() () () () ()

() () ()

() () () ()

LULU

LUL

ULULU

vHvHvHvH

vSvSvS

vSvSvSvSvS

vMvMvMvMvMvRank

112112111111

114114113

113112112111111

3221111

1111111111

++++













+++

++++

−+

++++=

()

1111

0823.000095.00823.000095.0

0.10.10.10.1905.0905.0

++++

+++++++−

+++++=vRank

Rank values for S1 are

{}

4877.5,8219.6,6119.8,9931.7,7214.9

with respect to 6 criteria respectively.

Similarly, the rank value for each alternative can be

obtained.

Step 4: The fuzzy positive-ideal solution

(

)

and fuzzy negative-ideal solution

(

)

−

Based on Eq. (4), fuzzy positive ideal solution and

fuzzy negative ideal solution are determined as

follows:

{}

3229.6,5526.9,5375.7,5526.9,7525.8,7214.9=

{}

4233.1,5259.3,1593.2,1805.1,8955.2,0533.0=

−

Using Eq.(5) to calculate the distance

)(

between each alternative and the ideal solution

)(

()()

3229.64877.57214.914.72.9 −++−= 

8858.1=

The distance between fuzzy negative ideal solution

and S1 calculated based on Eq.(6) as follows:

−

)(

()()

4233.14877.50533.014.72.9 −++−= 

4534.15=

Step 5: Using Eq.(7), the relative degree of

closeness

()

of each alternative

with respect

to the fuzzy positive ideal solution

.The

calculation for

shown as follows:

−

4534.158858.1

4534.15

8912.0=

Follow the same procedure to calculate

for

each alternative.

In the next step shows how the new criteria

1+n

involved in the evaluation of T2- FRBS

TOPSIS.

Step 6: The influence closeness coefficient

()

ICC

of each alternative

Firstly the influence degree

()

of each decision

maker must be determined using Eq.(8) based on

their experience on the field. In this case study,

in Table 4 represent the importance degree of

decision maker. DMs evaluate themselves by giving

value 0 to 10, for uninfluential and very influential

respectively. For instance influence degree of DM

is calculated as follows:

7108

32.0=

Following by Eq. (9) to get the influenced closeness

coefficient for

8912.032.0

×=ICC

2852.0=

Next, the influenced closeness coefficients need to

be normalized prior to matching the coefficient to

the linguistic terms in Table 3. As an example in this

case study, assuming the maximum value of

2852.0=

ICC

out of 25 stocks then the normalized

influenced closeness degree calculated as follows:

2852.0

=NICC

()

7214.9

=vRank

Interval Type 2- Fuzzy Rule based System Approach for Selection of Alternatives using TOPSIS

117

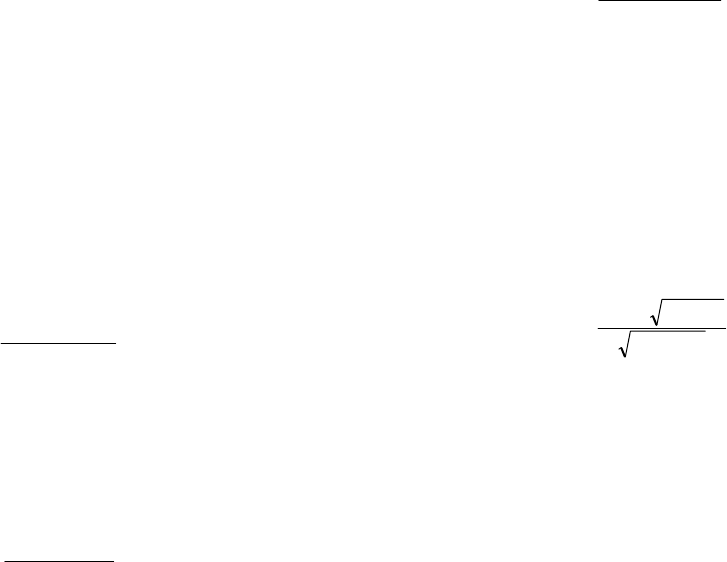
Step 7: The matrix of antecedent

()

and the

matrix of consequent

()

Each decision maker has t matrix of antecedent and

consequent separately.













mnmm

XXX









22221

11211

then















The rules have the following format:

is VG and

is VG Then

is VG.

Now, the value of

NICC

can be match to the

linguistic terms for alternative in Table 3. For

instance,

=NICC

Then

belong to interval type 2 fuzzy set VG in

Table 3.

Step 8: The final score

()

Γ for each alternative.

Based on Eq. (13) the value of final score has been

calculated. Assuming S1 has three rules R1, R2 R3

from three decision makers. For example final score

for S1 is shown below:

R1: If C1 is VG and C2 is VG and C3 is G and C4

is VG and C5 is G and C6 is G Then S1 is VG

R2: If C1 is VG and C2 is VG and C3 is F and C4 is

MG and C5 is MG and C6 is F Then S1 is VG

R3: If C1 is G and C2 is VG and C3 is VG and C4 is

VG and C5 is G and C6 is G Then S1 is VG

To calculate the value of

as in Eq. (14)

Let the output of each rule for S1 are as follows

R1: VG =(0.80,0.9,0.9,1.0,1.0,1.0)

(0.80,0.9,0.9,1.0,1.0,1.0)

R2: VG = (0.80,0.9,0.9,1.0,1.0,1.0)

(0.80,0.9,0.9,1.0,1.0,1.0)

R3: VG = (0.80,0.9,0.9,1.0,1.0,1.0)

(0.80,0.9,0.9,1.0,1.0,1.0)

Then,

is calculated as

9.09.09.0 ++

9.0=

Furthermore, the

is calculated using Eq. (15) as

follows

From Step 6, by assuming ICC of each rule for S1

are

R1: 1.0 R2: 1.0 R3: 1.0

The value of

defined as

0.10.10.1 ++

=Ω

0.1=

Lastly, the final score

()

can be derived as Eq. 13

Ω=

0.19.0 ×=

9.0=

Therefore, from the value of

, the ranking order of

all alternative can be determine. The best alternative

has higher value of

. Hence the ranking based on

proposed method (PM) can be seen in Table 4.

5 ANALYSIS OF RESULTS

For the validation purposes, the authors considered

the ranking based on established T2 TOPSIS (non-

rule based approach) and actual price change (return

on investment). The rankings are compared

descriptively using Kendall’Tau rank correlation

()

(Adler 1957). The advantages of Kendall tau

correlation are its easy algebraic structure and

intuitively simple interpretation. In general, the

coefficient of tau shows the degree of concordances

between two columns of ranking data. The Tau

Coefficient can be determine by



−

ijij

where

and

represent concordance pair and

discordances pair, respectively. In particular,

concordance pair interprets the number of observed

ranks below a particular rank which are larger than

that particular rank, whereas discordance is the

number of observed ranks below a particular rank

which are smaller than that particular rank. To test

the significant of the rank, the statistical z-score can

be define by following (Dibley & Trowbridge 1987).

)52(2

)1(3

−∗∗

Obviously, statistical z-score shows how far that

data is from the mean. The distance from the mean is

measured in term of standard deviation. The bigger

the z- score value, the more significant the ranking

to the actual ranking. Thus, based on the analysis of

Kendall’Tau Correlation in Table 5, it’s observed

that the z-score value of FRBS T2 TOPSIS is higher

than, which is outperform and more significant to

the actual ranking comparison to T2-TOPSIS.

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

118

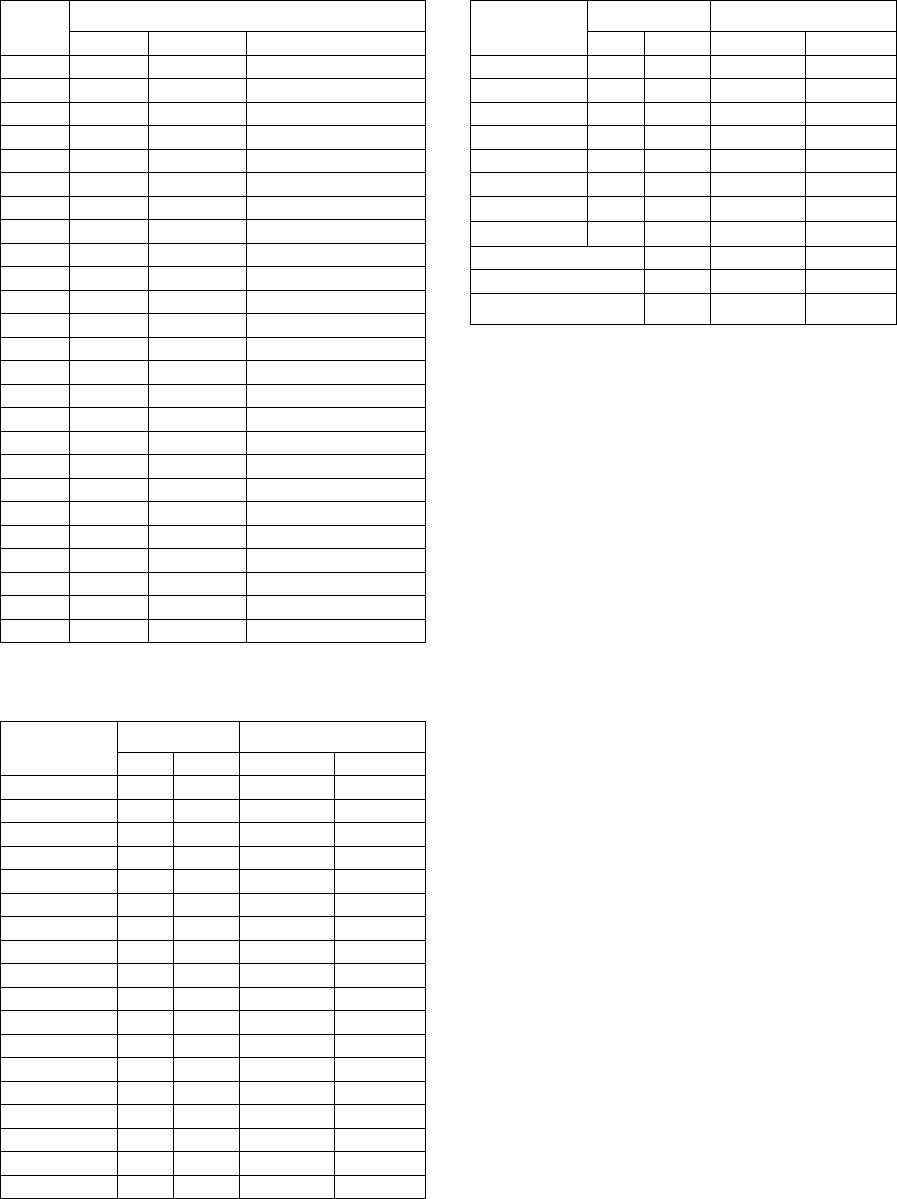
Table 4: Ranking based investment return, established T2

TOPSIS and proposed method (T2-FRBS TOPSIS).

Stock

Ranking

Actual T2-TOPSIS T2-FRBS TOPSIS (PM)

S3 1 24 24

S1 2 1 1

S15 3 15 10

S2 4 16 13

S16 5 9 8

S23 6 3 4

S21 7 11 11

S11 8 10 7

S14 9 13 15

S25 10 6 19

S6 11 19 17

S18 12 14 12

S12 13 4 3

S24 14 22 25

S19 15 23 22

S20 16 5 5

S7 17 2 2

S17 18 17 18

S5 19 21 21

S22 20 20 20

S4 21 7 6

S10 22 12 14

S9 23 25 23

S8 24 8 9

S13 25 18 16

Table 5: Assessing the ranking performance based on

Kendal’s tau correlation.

STOCKS

T2-TOPSIS T2- FRBS TOPSIS (PM)

S3 1 23 1 23

S1 23 0 23 0

S15 9 13 14 8

S2 8 13 11 10

S16 13 7 14 6

S23 18 1 17 2

S21 11 7 12 6

S11 11 6 13 4

S14 9 7 9 7

S25 12 3 5 10

S6 5 9 6 8

S18 7 6 8 5

S12 11 1 11 1

S24 2 9 0 11

S19 1 9 1 9

S20 8 1 8 1

S7 8 0 8 0

S17 4 3 3 4

Table 5: Assessing the ranking performance based on

Kendal’s tau correlation (cont.).

STOCKS

T2-TOPSIS T2- FRBS TOPSIS (PM)

S5 1 5 1 5

S22 1 4 1 4

S4 4 0 4 0

S10 2 1 2 1

S9 0 2 0 2

S8 1 0 1 0

S13

Summation 170 130 173 127

0.1333 0.1533

z 0.9342 1.0743

Kendal Tau Coefficient

0.8238

0.8577

6 CONCLUSION

In this paper, a novel variation of TOPSIS method

via extending established T2-TOPSIS method (Chen

and Lee 2010) by attached the ability of fuzzy rule

based system approach in solving the multi criteria

decision making problems. The ranking based on

proposed method is validated comparatively using

Kendall tau correlation. The results shows proposed

method (PM) outperform the established non rule

based version of type 2 TOPSIS in term of ranking

performance. The proposed method not only

provides a useful way to handle MCDM problems in

a more flexible and intelligent manner also presents

expert knowledge more accurately. In this paper,

the authors have successfully extended established

T2-TOPSIS using fuzzy system. The next objective

is to implement T2-TOPSIS using fuzzy networks,

which is new type of fuzzy system by aiming to

improve significantly the transparency of the

TOPSIS method.

REFERENCES

Adler, L.M., 1957. A Modification of Kendall’s Tau for

the Case of Arbitrary Ties in Both Rankings. Journal

of the American Statistical Association, 52(277),

pp.33–35 CR –

Awasthi, A., Chauhan, S.S. & Omrani, H., 2011.

Application of fuzzy TOPSIS in evaluating sustainable

transportation systems. Expert Systems with

Applications, 38(10), pp.12270–12280.

Chen, C.-T., 2000. Extensions of the TOPSIS for group

decision-making under fuzzy environment. Fuzzy Sets

and Systems, 114(1), pp.1–9.

Interval Type 2- Fuzzy Rule based System Approach for Selection of Alternatives using TOPSIS

119

Chen, S.-M. & Lee, L.-W., 2010. Fuzzy multiple attributes

group decision-making based on the interval type-2

TOPSIS method. Expert Systems with Applications,

37(4), pp.2790–2798.

Dibley, J. & Trowbridge, L., 1987. Interpretation of Z-

score anthropometric from the international growth

derived.

Hwang, C.L.Yoon, K., 1981. Multiple Atribute Decision

Making: Methods and Applications, New York:

Springer- Verlag.

Kelemenis, A., Ergazakis, K. & Askounis, D., 2011.

Support managers’ selection using an extension of

fuzzy TOPSIS. Expert Systems with Applications,

38(3), pp.2774–2782.

Lee, L. & Chen, S., 2008. Fuzzy multiple attributes group

decision-making based on the extension of TOPSIS

method and interval type-2 fuzzy sets. Machine

Learning and Cybernetics, (July), pp.12–15.

Mohamad, D. & Jamil, R.M., 2012. A Preference Analysis

Model for Selecting Tourist Destinations based on

Motivational Factors: A Case Study in Kedah,

Malaysia. Procedia - Social and Behavioral Sciences,

65, pp.20–25.

Santos, F.J.J. & Camargo, H.A., 2010. Decision support

systems in multicriteria groups: An approach based on

fuzzy rules. International Conference on Fuzzy

Systems, pp.1–8.

Şengül, Ü. et al., 2015. Fuzzy TOPSIS method for ranking

renewable energy supply systems in Turkey.

Renewable Energy, 75, pp.617–625.

Shidpour, H., Shahrokhi, M. & Bernard, A., 2013. A

multi-objective programming approach, integrated into

the TOPSIS method, in order to optimize product

design; in three-dimensional concurrent engineering.

Computers & Industrial Engineering, 64(4), pp.875–

885.

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

120