Low Aerodynamic Drag Suit for Cycling

Design and Testing

Live Spurkland, Lars Morten Bardal, Lars Sætran and Luca Oggiano

Norwegian University of Science and Technology, Deparment of Energy and Process Engineering,

K.Hejes vei 2b, 7042 Trondheim, Norway

Keywords: Cycling, Aerodynamics, Wind Tunnel Testing, Garments, Fabric.

Abstract: The focus on garment aerodynamics is increasing in high velocity sports where aerodynamics is crucial such

as cycling, speed skating and alpine skiing. Recently published research show that a low drag suit

manipulating the flow around the body can considerably enhance an athlete’s performance. This project

seeks to improve the Norwegian sportswear manufacturer Trimtex Sport AS’ pro cycling kit using the best

currently available textiles. Changes from the original design are made with the intention of optimizing

fabric zones and seam placement. Drag measurements on cylinder models, cyclists and full-scale

mannequins of the upper and lower body were conducted in the wind tunnel. The reduction in aerodynamic

drag was significant on cylinders, and final power savings of 8 watts due to drag reductions was obtained on

the jersey and 5 watts on the bib shorts for a cyclist racing at 50 km/h.

1 INTRODUCTION

Road cycling is one of the sports with high velocities

and infinitesimal time gaps where marginal gains are

crucial. Aerodynamic drag accounts for as much as

90% of the total resistance to be overcome when

cycling at a normal race pace, 70% of which is

created by the rider (Underwood and Jermy, 2011).

Aerodynamic drag can be expressed as

= 0.5c

(1)

where C

denotes the drag coefficient, ρ the air

density, U the air flow velocity and A the projected

frontal area (White, 2006). Besides optimizing the

rider’s position and suit fit to reduce the frontal area,

it is possible to reduce the total drag by improving

the surface texture of the rider’s clothing and thus

achieve a lower drag coefficient (Underwood, 2012;

Chowdhury et al., 2010).

Research on sport garment aerodynamics has

been progressing since the Nike Swift Spin project

based on the work by Brownlie in the early 2000.

Over 200 fabrics were tested and their final suit

offered a 3,9% reduction in F

compared with the

typical 2001 suits worn by competitors (Brownlie,

2009). Some of the most renowned brands of bike

clothing have recently been improving their time

trial suits by full-scale testing of suits with different

textiles in wind tunnels (Baker, 2010; Bioracer,

2014). Even though the results have been good, the

typical textiles used in regular road race cycling

suits on all levels are still smooth and seemingly

made only with focus on fitting and breathability.

However, a low drag cycling kit can give the

necessary advantage in a road race by reducing the

effort needed at a given velocity. The 1989 Tour de

France was won by Greg LeMond by a winning

margin of 8 seconds and by Alberto Contador in

2007 by 23 seconds illustrating the minuscule

margins and the need for perfectionism in the

cycling sport.

It is known that the drag coefficient of bluff

bodies suddenly drops at a certain critical velocity

during transition from laminar to turbulence flow in

the boundary layers (Zdravkovich, 1990) commonly

called the drag crisis. The Reynolds number at

which the drop occurs, the magnitude of the drop

and the subsequent rate of increase in C

is highly

dependent on the surface roughness (Achenbach,

1971). A rough surface induces an early transition

but at the same time decreases the drop and

increases the post-critical drag coefficient (Auteuil

et al., 2010). Hence, the flow around a bluff body

can be manipulated by mixing various patches of

textile with different surface morphology to prevent

or delay flow separation at strategic places.

The aim of this work is to find the material and

Spurkland, L., Bardal, L., Sætran, L. and Oggiano, L..

Low Aerodynamic Drag Suit for Cycling - Design and Testing.

In Proceedings of the 3rd International Congress on Sport Sciences Research and Technology Support (icSPORTS 2015), pages 89-96

ISBN: 978-989-758-159-5

design that could improve the overall aerodynamic

performance of the pro cycling suit produced by

Trimtex Sport AS using facilities in the wind tunnel

laboratory at the Department of Energy and Process

engineering at the Norwegian University of Science

and Technology (NTNU). In the preliminary tests,

cylinders are covered with 27 different fabrics and

tested in a wind tunnel to separately assess the flow

around each body part. This method has been used

in several previous studies with good results (Bardal

and Reid, 2012: Chowdhury et al., 2010, Underwood

and Jermy, 2011; Oggiano et al., 2013). The most

promising fabrics were also tested on tandem

cylinders and with a steel grid creating intense

turbulent flow in the tunnel. Two different cycling

kits with the original design but patched with the

new materials and one jersey with an alternative

design have been tested on both cyclists and full-size

upper and lower body mannequins.

1.1 Rules and Regulations

According to the UCI (Union Cycliste

Internationale) regulations for clothing material,

only “plain textile material” with no other purpose

than that of clothing can be used. Textile is here

defined as “a material made up of yarns and fibres

which has an open mesh “fabric” structure”. No

seams should be present on a suit that does not hold

two pieces of fabric together and coating other than

logos and labels are not allowed .The apparel should

serve the unique purpose of clothing and has to

“conform to the curve of the body in any case”

without any “non-essential parts” to improve

aerodynamic resistance (UCI, 2012). All materials

tested in this project comply with the UCI

regulations.

2 METHODS

2.1 Fabric Testing

2.1.1 Experimental Setup

The measurements were conducted in a small scale

wind tunnel at NTNU with a cross section of

0,55x1,0 meters and a maximum wind speed of 28

m/s. To measure the wind speed, a pitot tube was

placed 2,70 m in front of the cylinder. The

temperature was monitored by a thermocouple type

K (chromel-alumel) and its value used to calculate

density and dynamic viscosity of the airflow. The

forces on the cylinder were measured by an AMTI

BP400600HF force plate that consists of strain

gauges in three directions. In this experiment, only

the drag- or y-direction force was used.

When riding aggressively, the shoulder and

upper arm are positioned perpendicular to the flow.

Riding slightly more upright, the angle increases to

10 or 15 degrees. The critical Reynolds number

remains constant with various angles of attack while

a rough surface reduces cylinder drag for angles up

to 25 degrees (Oggiano et al., 2013; Chowdhury,

2012). Testing was therefore conducted on cylinders

positioned with the long axis perpendicular to the

flow. The fabrics for the torso was also tested on a

vertical cylinder as the differences in friction drag

can be foreseen from a vertical cylinder

measurement (Bardal and Reid, 2012).

Two circular cylinders with diameters of 11 and

16 cm were used. The smallest cylinder was 40 cm

long with a gap of 9,7 cm above and 5,0 cm below

while the largest cylinder was 47 cm long with 4,3

cm above and 3,4 cm below. The smooth fabrics for

the torso were tested on the 16 cm diameter cylinder

because of the lower velocity drag crisis on this

cylinder, while the rougher fabrics were tested on

the 11 cm diameter cylinder.

The steel grid used to create turbulence had

circular bars 10 mm in diameter and cells of size

40x40 mm that covered the whole cross section of

the tunnel. It was placed 0,35 m behind the pitot

tube and 2,35 m in front of the cylinder. The flow

produced by the grid was probably of too high

turbulence intensity compared with normal outdoor

conditions although it was not measured.

Nevertheless, the results indicate how disturbances

in the flow affect the drag of various surface

structures.

For the measurements with tandem cylinders, the

11 cm diameter cylinder was placed with a

separation distance of 17 and 23 cm in front of the

larger cylinder of 16 cm diameter. Drag was

measured on the second cylinder only. This

configuration is a simplification of one limb in front

of another such as an arm in front of a thigh.

2.1.2 Textiles

The fabrics were fitted with 25% stretch. According

to Oggiano (Oggiano et al., 2013), there is a weak

linear relation between the critical velocity and the

stretching of the fabric, but he concludes none the

less that it does not seem to affect the flow

transition. Bardal found that stretch is of no practical

significance in the design of alpine skiing suits

(Bardal and Reid, 2012). The textiles tested in this

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

project are significantly thinner than textiles used in

an alpine suit, so it may all the same be a minor

factor. All textiles were tested with the seam centred

on the leeward side to minimize its influence.

Sublimation printing was done prior to testing since

the print makes the surface smoother and thereby

changes the aerodynamic properties (Oggiano et al.,

2013).

Figure 1: Upper and lower body mannequins.

2.2 Full Scale Testing

2.2.1 Experimental Setup

Testing of the cycling kits on the mannequin models

and cyclist were conducted in the large wind tunnel

at NTNU. It is equipped with a 220KW fan engine,

has a maximum speed of 30 m/s and the test section

measures 2,7x1,8x12,5 meters. A pitot tube and a

thermocouple type K was used to monitor the wind

speed and temperature respectively. The drag was

measured with a Schenck six component force

balance where only the axis of the drag direction

was used. The drag forces presented are normalized

to 20 degrees celsius.

2.2.2 Mannequin Models

Testing on both mannequin models was conducted at

five velocities ranging from 35 to 72,5 km/h or 9,7

to 20,1 m/s. The mannequin used for testing the

jersey was a full-scale upper body including head

and upper arms belonging to a model of height 170

cm and weight 70 kg. Its position was adjusted to

imitate that of a cyclist in the drop bars and the

forearms removed to reduce the amount of

uncertainty. The lower body mannequin had an inner

leg length of 90 cm with a mid-thigh circumference

of 58 cm. Only one leg was used with the other cut

at 16 cm. A 1,0 cm thick plate fixed the loose part of

the shorts. Photographs of the mannequins are

presented in Figure 1.

Figure 2: Cyclist in an upright dropped position.

In addition to drag measurements of the jerseys,

measurements were conducted on all combinations

of jerseys and sleeves to investigate the

contributions from sleeves separately. To examine

the importance of sleeve length, drag measurements

were conducted with the mannequin wearing

nothing but the different sleeves in both the original

length (17 cm) and elbow length (30.5 cm). Note

that when the original length is used on the loose

sleeves, they do not have the smooth 4 cm bi-elastic

band at the ends. The loose sleeves therefore have

the sleeve material 4 cm longer than the jersey

sleeves.

2.2.3 Cyclist

A regular road bike was placed on a roller so that the

tires were not touching the wind tunnel floor. The

front wheel was kept stationary and supported by a

custom-made wheel stand. The back wheel was only

spinning in the dynamic tests. The cyclist was

positioned comfortably in the drop bars and live

video acquired from a side-mounted camera was

projected on the floor in front of the rider. The video

was showing the position superimposed with an

outline of the initial position in order to keep it as

consistent as possible.

Mean values of the drag force were calculated

from three times 30 seconds dynamic pedalling on a

cadence of 90 RPM and three times 30 seconds

static with left leg at 0 degrees (Figure 2). This was

done alternately a total of three times at each of the

velocities, 35, 50 and 65 km/h (9,7, 13,9 and 18,1

m/s).

Low Aerodynamic Drag Suit for Cycling - Design and Testing

Table 1: Mean velocity distribution from an assortment of

men’s elite road races.

26-35kmh

(7-10ms)

36-45kmh

(10-13ms)

46+kmh

(13+ms)

National 0.267 0.378 0.356

International 0.241 0.408 0.351

Total average 0.254 0.393 0.354

2.3 Speed and Force Calculations

Based on a total of eleven men’s elite road races, the

mean velocity distribution for three domains was

found. Not counting velocities less than 25 km/h, the

percentage of total time in each domain is listed in

Table 1. The velocity profile was used to calculate

the weighted mean drag of the materials.

Assuming similar conditions for an individual

time trial (ITT) as in a solo breakaway or in front of

the peloton, ITT races are used to illustrate time

savings of the various apparel. Theoretical time

savings were calculated using Bassett's empirical

model (Bassett, 1999) from his study of hour records

from 1967 to 1996. The dropped position on the

road is identical to that of Eddy Merckx in 1972, but

modern bicycles and cycling suits have lower drag

than those used in Bassett's study. The power P

needed to overcome air and rolling resistance on a

cycling track is:

= 0.00953

V + 0.00775V

+ 0.007551

(2)

M is the total weight of the cyclist and the bike in

kilos, A is the frontal area and V is the velocity.

The time savings are illustrated on two

constructed persons. Person 1 has a weight of 70kg,

person 2 60 kg and the bikes 7 kg. With respective

heights of 1.83 and 1.70m correspondingly, the

frontal areas of person 1 and 2 are 0.337 and

0.308m

using Bassett’s formula for frontal area

(Bassett, 1999).

3 RESULTS

3.1 Jersey

3.1.1 Fabric Testing

The results from the cylinder tests of the original and

chosen jersey materials are shown in figure 3 plotted

against the velocity normalized to common racing

conditions of 20 degrees and 1 atm. Table 2 shows

the material used on the various jersey patches.

Figure 3: Jersey material on 11 and 16 cm cylinders. The

values are normalised with the sub-critical C

Table 2: Material used in the different fabric zones.

Jersey A Jersey B Jersey C

Front #2 #3 #3

Back #1 #3 #3

Upper Back #2 #5 #3

Sides #1 #5 #4

Sleeves #3 #5 #6

Whereas the original jersey (A) has relatively

smooth materials on all panels, the differences in

surface roughness on the new jerseys are more

pronounced. Since the flow pattern around a cyclist

throughout a stroke is asymmetrical with an “S”

forming on his back (Crouch et al., 2012), the fabric

on the back should be homogenous and as smooth as

possible such as fabric #3. This thin and breathable

fabric is used on the front and back on jerseys B and

C. Fabric #5 has an asymmetrical mesh-like

macrostructure similar to prism formed dimples with

microstructure in the dimples and no fuzziness while

fabric #6 has a traditionally dimpled structure with a

smooth surface. With a minimum drag coefficient of

0.47 at Reynolds number 107 000, fabric #5 seems

equally or better suited to enhance transition on the

prioritized velocities than most textiles tested by

others (Chowdhury et al., 2010; Brownlie et al.,

2009; Bardal and Reid, 2012). The weighted mean

of the drag coefficients of fabric #5 was 0.686 while

the mean for #6 was as low as 0.652 due to its lower

post-critical drag. The latter could be owing to its

smooth and dimpled surface structure since this can

reduce post-critical drag with respect to other kinds

of structure (Zdravkovich, 1990; Bearman and

Harvey, 1993; Oggiano et al., 2013). Fabric #5 is

used on the sleeves, sides and top of the back of

jersey B aiming to enhance transition to turbulence

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

in the boundary layer at the patches most exposed to

the free stream. Jersey C is a compromise between

jersey A and B with fabric #6 on the sleeves and the

sheer and semi-smooth fabric #4 on the sides.

The resulting drag profiles using the steel grid

show, as expected, that a less rough surface structure

is needed to enhance transition at the same velocities

when the flow is turbulent. The fact that smoother

materials were more influenced by the turbulence

emphasizes the importance of a smooth surface

where friction drag is dominant such as on the back

of a cyclist. These effects are also observed for the

tested bib fabrics. The intense turbulence amplified

the post-critical differences in drag for fabric #5 and

#6 from 3,5 to 5%, possibly indicating an

accentuated effect of dimpled surfaces in turbulent

flow. The smoother surface of fabric #6 is most

likely an important factor as well although it did not

alter the critical velocity with respect to fabric #5.

3.1.2

Full Scale Testing

The jerseys were tested on the mannequin against

the original Trimtex Pro cycling jersey. Whereas the

drag coefficients of jersey B and C are constant and

nearly identical, the original jersey A clearly has a

higher drag at low speeds as seen in figure 4. The

difference decreases with increasing velocity and

stabilizes at 15 m/s. The improvement in drag force

is 25-35 grams at all velocities with a standard

deviation of 8 grams or 0.37%. Table 3 shows how

the performance is improved by the reduced drag.

The fact that the drag on jersey B and C were nearly

identical can indicate that the sleeves are the largest

contributor, and that the rougher panels on jersey B

do not have a significant impact on the flow.

Figure 4: Jerseys tested on mannequin with error bars.

To study how the drag is affected by sleeve

roughness alone, loose sleeves of the respective

qualities where placed on top of the original jersey.

Figure 5 shows that the drag is nearly equal for all

sleeves up to 14 m/s where the rougher sleeves have

similar and increasingly lower drag at higher

velocities. At 19 m/s the difference is 26 grams for

#5 and 43 grams for #6 compared with sleeve #3.

Lengthening the loose sleeves to the elbows, the

overall drag is lowered with the ratios kept constant

so that the difference between the sleeves doubles to

54 grams for #5 and 87 grams for #6. These

differences are expected based on the cylinder

measurements and are assumed to be a result of the

dimpled surface structure of fabric #6. Note that the

drag obtained with loose sleeves cannot be

compared directly to the drag of the full jerseys

since the loose sleeves are tucking in some extra

fabric in the armpits.

Figure 5: Effects of sleeve length and roughness from the

mannequin tests with error bars showing the standard

deviation.

Both figure 4 and 5 indicate a critical velocity at

13-15 m/s on jersey A that corresponds to Reynolds

number 85 000 for the arms of the mannequin. The

arm had a circumference of 28 cm, so these results

are in good correspondence with the critical velocity

of fabric #5 and #6 at Reynolds number 85 000 on

the 11 cm cylinder. The transitions seem to have

taken place at even lower velocities for jersey B and

C due to the rougher patches. However, the effect of

a rough sleeve fabric will in all probability be less

on a cyclist than on the mannequin due to increased

disturbance in the flow.

A fourth jersey (D) was designed based on the

mannequin tests. Its materials are similar to those of

jersey C but the sleeves are extended by 2 cm and

the elastic grip has a slightly structured surface. The

elastics on both sleeves and pockets are tightened to

minimise flapping. The side panel is wing shaped so

that the seam runs in the stream-wise direction to the

back extending the front patch along the lower sides

of the jersey.

Figure 6 shows the drag difference of jersey B, C

and D with respect to the original jersey (A) when

Low Aerodynamic Drag Suit for Cycling - Design and Testing

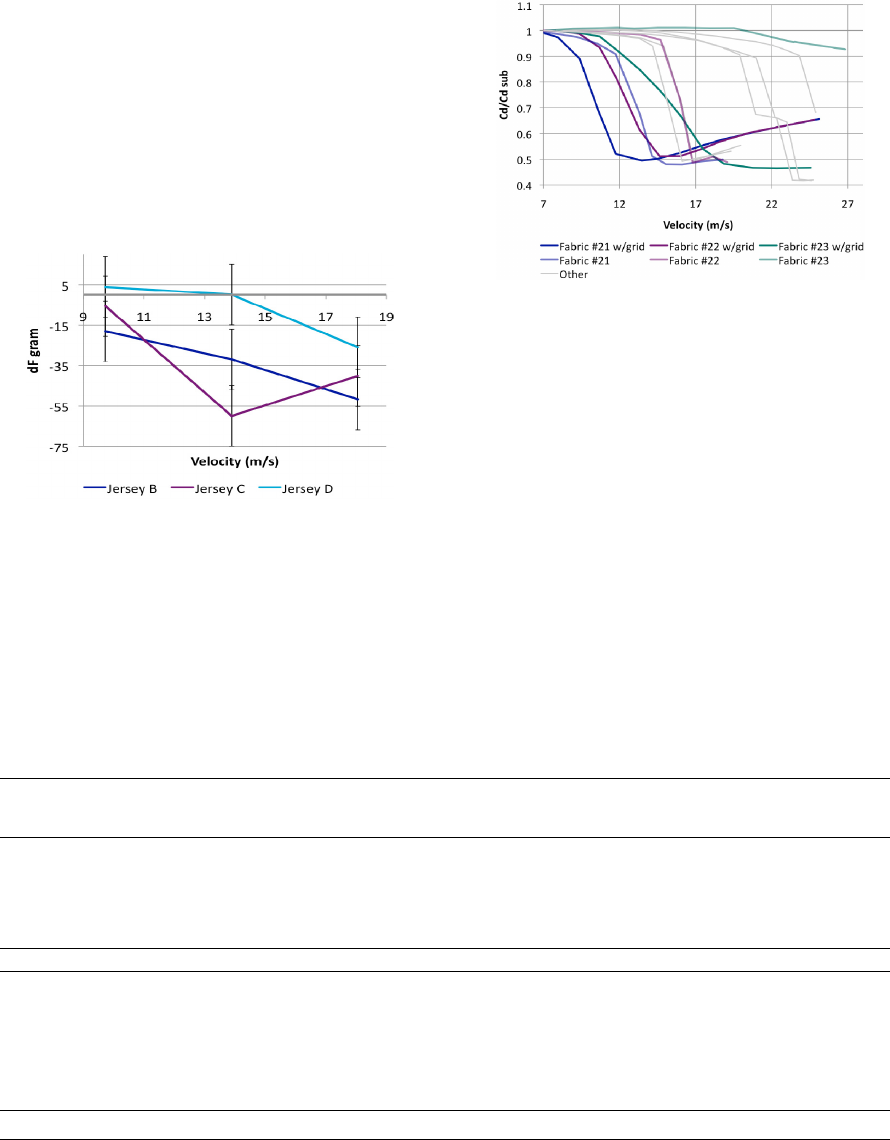
tested on the cyclist. All jerseys have similar

properties at 9,7 m/s, but the rougher jerseys have a

clear advantage at higher velocities. Surprisingly,

jersey D had higher drag than the other jerseys

despite the assumed profitable changes in design. By

tightening the pocket band, wrinkling perpendicular

to the flow increased somewhat on the sides of the

torso. This could be the main reason for the increase

in drag compared with jersey C since the material in

the side panels do not seem to play a critical role. As

listed in table 3, the improvement of jersey C with

respect to the original jersey is of 60 grams or 8.2

watts at 13,9 m/s (50 km/h).

Figure 6: Dynamic testing on cyclist. Difference in drag

(grams) of jersey B, C and D compared with jersey A,

with error bars.

The dynamic tests show approximately 5% lower

drag than the static tests, and the differences

between the jerseys were smaller, probably due to

the fact that leg motion will trigger flow transition

(Brownlie et al., 2009). The standard deviations

were 15 grams or 0.33% for the dynamic tests and

19 grams or 0.43% for the static tests.

Figure 7: Bib fabric with and without grid on a 16 cm

diameter cylinder. The C

-values are normalised with

sub-critical C

Wearing a correctly fitted jersey is of outmost

importance. The jersey in size small fitted the cyclist

comfortably yet tightly with few wrinkles and would

be the natural choice for a racing jersey. The

medium-sized jersey was still relatively tight and

well fitted, but the wrinkles on the side panels were

more pronounced. This seemingly small difference

in size increased the

drag by 104 grams or 14 watts

at 50 km/h, as shown in the last line of Table 3.

3.2 Bib Shorts

3.2.1 Fabric Testing

The flow around the thighs is the most difficult to

Table 3: Theoretical drag, power and time savings of the various jerseys and bibs at 50km/h compared with the original kit.

Mannequin

Drag

difference (g)

Power

difference (W)

Drag increase* (%) Time difference 1h, 50km/h (s)

Person 1 Person 2 Person 1 Person 2

Jersey B -30 -4.1 -1.1 -1.2 -00:14 -00:16

C -33 -4.5 -1.2 -1.3 -00:15 -00:17

Bib B -9 -1.2 -0.3 -0.4 -00:04 -00:05

C -22 -3.0 -0.8 -0.9 -00:10 -00:11

Cyclist

Jersey B -32 -4.4 -1.2 -1.3 -00:15 -00:17

C -60 -8.2 -2.2 -2.4 -00:28 -00:31

D 0 0 0 0 00:00 00:00

Bib B -4 -0.5 -0.2 -0.2 -00:02 -00:02

C -35 -4.8 -1.2 -1.4 -00:16 -00:18

Sizing

Jersey size M +104 +14.2 -3.8 -4.2 +0:48 +00:53

*From 374W for person 1 and 340W for person 2

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

predict as the free stream flow is disturbed upstream

by the front wheel, cockpit and forearms in addition

to the thigh movements. As the flow regime

characterizing the aerodynamics of a cyclist changes

throughout the stroke cycle, materials with an

asymmetrical pattern having varying properties

depending on the leg position could present an

interesting compromise. When in the upper part of

the stroke, the air remains attached alongside the

thigh and follows a downward trajectory into the

wake. With the leg perpendicular to the flow, the

flow separates over the hip following an upward

path into the wake (Crouch et al., 2012). A striped

pattern aligned with the thigh would therefore be

alternately in line with the flow having the

properties of a smooth fabric and perpendicular to

the flow enhancing transition. Various striped

patterns were tested against traditional smooth

materials and fabrics with a homogenous structure.

On the 16 cm cylinder, a broadly striped material

with a smooth surface (#21) had the lowest critical

velocity while the original smooth fabric #23 did not

undergo transition even at 25 m/s. A narrowly

striped fabric (#22) with properties in between of the

two extremes was chosen alongside fabric #21 for

further testing against the original bib. The results

are shown in Figure 7 both with and without grid in

the tunnel and favour the broadly striped fabric.

With the cylinders in tandem configuration, a rough

surface texture is desired at the rear cylinder

regardless of the distance to and surface roughness

of the cylinder in front. Nevertheless, the importance

of the material on the second cylinder decreased

significantly with decreasing distance between the

two cylinders. The effect is similar to that of the grid

produced turbulence confirming that disturbances in

the flow reduce the effect of surface roughness.

3.2.2 Full Scale Testing

Bib A is the original bib with fabric #23 while fabric

#21 and #22 is used on bib B and C respectively.

Testing on the one-legged lower body mannequin

was conducted to study the effect of three-

dimensional effects due to the shape of the thigh

muscles. A clear drop in the drag coefficient is seen

in Figure 8 for all bibs at 15 m/s, but eventual

variations in critical velocity are not pronounced.

The original smooth bib had highest sub-critical drag

while bib C had the lowest. The super-critical values

were similar for all bibs. A fourth bib with a slightly

rougher bi-elastic band was also tested, but the

influence was too small to be observed. The standard

deviations were 10 grams or 0,53%.

Figure 8: Bib shorts tested on mannequin with error bars.

When tested on the cyclist, the difference

between bib A and B was less than the standard

error on both the dynamic and static tests while bib

C had the lowest drag in both cases with 35 grams or

5 watts less drag than bib A at 50 km/h. The results

presented in Figure 9 indicate that bib B enhanced

transition at velocities slightly lower than bib A and

that the rough surface of bib C led to the highest

super-critical drag. These changes in properties

compared with the cylinder measurements may be

explained by increased stretching of the fabrics on

the mannequin and the cyclist. The surface structure

of bib B became less pronounced than on the

cylinder and bib C got a rougher, more homogenous

surface.

Figure 9: Dynamic testing on cyclist. Difference in drag

(grams) of bib B and C compared with bib A, with error

bars.

4 CONCLUSION

The cycling kit developed in this project has

considerably lower drag than a traditional kit with

smooth fabrics only. Rough material on the sleeves

clearly improves the aerodynamic qualities of a

jersey, and the results indicate that dimpled fabric

having a smooth surface is favourable to other types

of surface morphology. Since the gain increases with

Low Aerodynamic Drag Suit for Cycling - Design and Testing

sleeve length, the sleeves should be as long as

comfort and regulations allow. A structured surface

is preferred on bib shorts as well. The rough

materials tested in this project were the roughest

currently available fabrics both complying with the

UCI regulations and suitable for use in a cycling kit.

It is likely that a sleeve and bib material with a more

pronounced surface structure could further reduce

the drag. Jersey designs with the seams to a greater

extent in the stream-wise direction and distinctly

striped bib material are of particular interest for

future work.

The results from this project can be applied to

other cycling garments. Loose sleeves normally have

a smooth fabric all over but should rather have a

rough surface on the part covering the upper arms.

The same applies to time trial suits. Loose legs

should probably be of the same material as the bib

shorts above the knee, and transition could be

induced on the lower leg by a rougher material

(Brownlie et al., 2009) as in speed skating (Sætran

and Oggiano, 2008). Aerodynamic shoe covers

should likewise be roughly structured above the calf.

REFERENCES

Achenbach 1971. Influence Of Surface Roughness On The

Cross-Flow Around A Circular Cylinder. Journal Of

Fluid Mechanics, 46, 321-335.

Auteuil, Larose & Zan 2010. Relevance Of Similitude

Parameters For Drag Reduction In Sport

Aerodynamics. 8th Conference Of The International

Sports Engineering Association (Isea). Elsevier L.Td.

Baker. Dec 10. 2010 2010. Testing Velocity Speedsuit At

The A2 Wind Tunnel. Available From:

Http://Blog.Hincapie.Com/Post/Testing-Velocity-

Speedsuit-At-The-A2-Wind-Tunnel.Aspx 2014].

Bardal & Reid 2012. Testing Of Fabric For Use In Alpine

Ski Competition Suits. Engineering Of Sport

Conference 2012. Elsevier Ltd.

Bassett 1999. Comparing Cycling World Hour Records,

1967-1996: Modelling With Empirical Data. Medicine

& Science In Sports & Exercise, 31.

Bearman & Harvey 1993. Control Of Circular Cylinder

Flow By The Use Of Dimples. American Institute Of

Aeronautics And Astronautics Journal, 31.

Bioracer. 2014. Bioracer Speedmaster, Medal Winning

Technology [Online]. Bioracer. Available:

Http://Www.Bioracer.Com/En/News/318/Bioracer-

Speedmaster-Medal-Winning-Technology [Accessed

Nov 8 2014].

Brownlie, Kyle, Carbo, Demarest, Harber, Macdonald &

Nordstrom 2009. Streamlining The Time Trial

Apparel Of Cyclists: The Nike Swift Spin Project.

Sports Technology Journal, 2, 53-60.

Chowdhury 2012. Aerodynamic Design Of Sports

Garments. In: Colman, D. J. (Ed.) Applied

Aerodynamics. Intech.

Chowdhury, Alam & Subic 2010. Aerodynamic

Performance Evaluation Of Sports Textile. 8th

Conference Of The Internationsl Sports Engineering

Association (Isea). Elsevier Ltd.

Crouch, Sheridan, Burton, Thompson & Brown 2012. A

Quasi-Static Investigation Of The Effect Of Leg

Position On Cyclist Aerodynamic Drag. Procedia

Engineering, 3-8.

Oggiano, Brownlie, Troynikov, Bardal, Sæter & Sætran

2013. A Review On Skin Suits And Sport Garment

Aerodynamics: Guidelines And State Of The Art. 6th

Asia-Pasific Congress On Sports Technology (Apcst).

Elsevier L.Td.

Sætran & Oggiano 2008. Skin Suit Aerodynamics In

Speed Skating. In: H., N. (Ed.) Sport Aerodynamics.

Cism International Centre For Mechanical Sciences.

Uci 2012. Clarification Guide Of The Uci Technical

Regulation In: (Uci), U. C. I. (Ed.) 23.04.2014 Ed.

Underwood. 2012. Aerodynamics Of Track Cycling.

Doctor Of Philosophy, The University Of Canterbury.

Underwood & Jermy 2011. Fabric Testing For Cycling

Skinsuits. Elsevier L.Td.

White 2006. Viscous Fluid Flow, Mcgraw Hill.

Zdravkovich 1990. Conceptual Overview Of Laminar And

Turbulent Flows Past Smooth And Rough Circular

Cylinders. Journal Of Wind Engineering And

Industrial Aerodynamics, 33, 53-62.

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support