Comparison of Sampling Size Estimation Techniques for Association

Rule Mining

gba Halıcı and Utku G

orkem Ketenci

Cybersoft R&D Center,

Istanbul, Turkey

Keywords:

Sampling, Association Rule Mining, Market Basket Analysis.

Abstract:

Fast and complete retrieval of individual customer needs and “to the point” product offers are crucial aspects

of customer satisfaction in todays’ highly competitive banking sector. Growing number of transactions and

customers have excessively boosted the need for time and memory in market basket analysis. In this paper,

sampling process is included into analysis aiming to increase the performance of a product offer system. The

core logic of a sample, is to dig for smaller representative of the universe, that is to generate accurate associa-

tion rules. A smaller sample of the universe reduces the elapsed time and the memory consumption devoted to

market basket analysis. Based on this content; the sampling methods, the sampling size estimation techniques

and the representativeness tests are examined. The technique, which gives complete set of association rules in

a reduced amount of time, is suggested for sampling retail banking data.

1 INTRODUCTION

Today’s highly competitive sales and marketing con-

ditions force companies to have a better understand-

ing of their customers’ needs. The strategic sales

and marketing decisions, which are based on the cus-

tomers’ purchasing proﬁle, succeed and increase the

proﬁtability of the companies.

Market basket analysis is a fundamental data min-

ing technique to identify the customers’ behaviors. It

is used to reveal the hidden patterns in the customers’

transactions and to mine the associations among prod-

ucts, that are often bought together. Conventional

market basket analysis consists of clustering and as-

sociation mining. Clustering is executed in order to

create groups of customers with similar marketing be-

haviors. Association mining takes place to ﬁgure out

patterns behind these behaviors and to understand the

current purchasing behavior of look alike customers.

However, analysis on large-scale databases be-

comes unaffordable due to time and memory con-

sumptions. In order to improve the memory con-

sumption, early studies introduced new association

mining algorithms (Hidber, 1999; Pei et al., 2000;

Hipp et al., 2000; Zhang et al., 2008; Pei et al., 2007;

Zaki and Hsiao, 2002). Other studies focused on sam-

pling for association mining so as to reduce both time

and memory consumptions (Zaki et al., 1997; Chakar-

avarthy et al., 2009; Toivonen et al., 1996; Riondato

and Upfal, 2012).

In this paper, sampling for association mining is

included into the market basket analysis. Based on

the assumption of “a good representative subset of

the transactions would not have any association rule

loss”, mining process is executed on the sample rather

than the universe.

To materialize this objective, this study ﬁrst inves-

tigates different sampling methods and their parame-

ters. We have identiﬁed sample size as the most im-

portant parameter, which impacts the representative-

ness of a sample and the time consumption of entire

mining process. To measure the success of represen-

tativeness of a sample, two statistical tests have been

used. Along with the results of the tests, we have

implemented two sampling methods by covering sev-

eral different techniques to specify the optimal sample

size. In addition, we tracked loss of association rules

in samples.

This paper focuses particularly on the sampling

methods and implementations for association mining

process in Section 2. The section of 2.1 deﬁnes the

sampling methods. Section 2.2 gives a formal deﬁni-

tion of sample size estimation techniques for associ-

ation rule mining. Section 3 covers the implementa-

tion of statistical tests for sample representativeness.

Dataset and test scenario are explained in Section 4.

Samples are compared in terms of the representative-

ness tests and derived association rules. A discussion

Halıcı, T. and Ketenci, U..

Comparison of Sampling Size Estimation Techniques for Association Rule Mining.

In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 1: KDIR, pages 195-202

ISBN: 978-989-758-158-8

195

of results and conclusions can be found in Section 5.

2 SAMPLING

Sampling is a statistical data selection method that

creates a representative subset of the universe. It is

mainly utilized whenever access to universe transac-

tions is impossible or computations on the universe

are resource-intensive. Association mining is a time

and memory consuming process, which makes the

sampling essential for efﬁcient use of memory and

time.

Early studies about sampling for association min-

ing show that there exists a sample which is similar to

the universe (Mannila et al., 1994). The subsequent

studies concentrate on ﬁnding a lower bound for the

sample size from different perspectives (Zaki et al.,

1997; Chakaravarthy et al., 2009; Toivonen et al.,

1996; Riondato and Upfal, 2012).

The main concern of association mining is the rep-

resentativeness of a sample. Loss of any association

rule is undesirable for a successful sample, hence the

patterns existing in the universe should remain in the

sample as well. Therefore, the sampling methods and

the sampling size estimation techniques play a signif-

icant role. Section 2.1 and Section 2.2 detail the dis-

cussion about sampling methods and sampling size

estimation techniques, respectively.

2.1 Sampling Methods

Sampling methods, which is the ﬁrst major factor dur-

ing sampling, specify the procedure to be followed

during the transaction selection. The methods are di-

vided into 2 groups, namely probability sampling and

non-probability sampling.

Probability sampling methods involve random

selection of transactions, whereas non-probability

methods do not. Randomness ensures that all trans-

actions in the universe have a chance of selection.

Non-probability sampling methods leave some trans-

actions out of coverage. Being not able to cover

all transactions in the universe, non-probability sam-

pling methods are not eligible for association mining.

Therefore, in this study, only the probability sampling

methods are considered.

Assume U is the universe where |U| = N. A sam-

ple s with |s| = n can be generated by utilization of

the following probability sampling methods;

- Simple random sampling: All transactions have

same the probability of being chosen. n many

transactions are selected from the universe ran-

domly.

- Stratiﬁed random sampling: Having a categoriza-

tion in the universe, this method could be pre-

ferred. Assume there exist m categories with N

transactions, then n

transactions are randomly se-

lected from i

category, where

∗ n

(1)

for all i ∈ [0, m − 1]. All transactions in a given

category have the same probability of being cho-

sen.

- Systematic sampling: All transactions have the

same probability of being chosen. Transactions in

the universe are sorted and divided into k groups,

where

k =

, (2)

the ratio between universe size and sample size.

A random number i ∈ [0, n − 1] is generated as an

index for each group. Every i

transaction from k

groups is selected for placement into sample.

- Cluster sampling: Homogeneous clusters of uni-

verse are formed, each of which has n transac-

tions. A random number j ∈ [0, k − 1] is gener-

ated, where

k =

, (3)

the ratio between universe size and sample size.

The j

cluster is designated as sample.

- Multistage sampling: In the ﬁrst stage, homoge-

neous clusters of universe are formed. Later, a

subset of the clusters is selected by simple ran-

dom sampling. In the last stage, n transactions

are selected from the subset of clusters using sim-

ple random sampling again. All transactions in a

given cluster have the same probability of being

chosen.

The applicability of the methods depends on the

properties of the universe. The dataset for associa-

tion rule mining consists of binary values. Each value

shows the existence of relation between the customers

and the products. The customers and the products are

represented by rows and columns, respectively.

Simple random sampling is an exceptional and

easy to apply method, which is independent of the

dataset. Similarly, stratiﬁed random sampling can

be executed for association rule mining in large

databases. It is useful when the representation of the

subgroups is crucial. The strata are generated by com-

binations of products. For instance, four strata are cre-

ated from two products, say A and B. These strata are

only A holders, only B holders, both A and B holders

and neither A nor B holders.

KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval

196

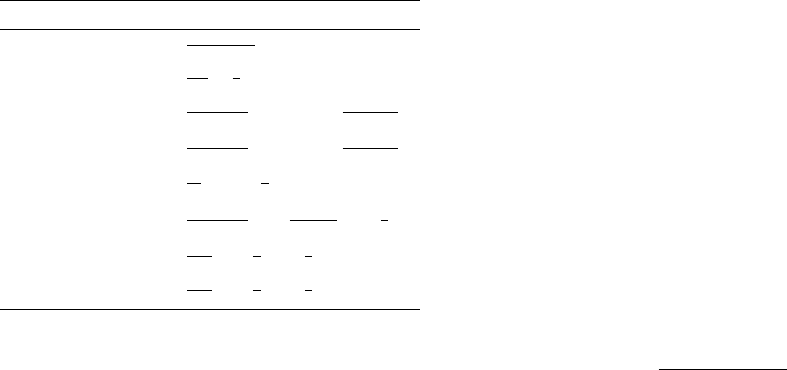
However, sampling methods such as systematic

sampling require a numerical value for sorting. The

determination of this value is a crucial task for a cor-

rect sampling. In our case, this method cannot be ap-

plied due to lack of numerical values in the universe

dataset.

Cluster sampling and multistage sampling use

“natural” clusters such as geographical areas. These

clusters must be homogeneous. In case where no nat-

ural homogeneous clusters found such as customer-

product ownership data including only binary values,

these methods cannot be applied either.

2.2 Sampling Size Estimation

Techniques

The second major factor for sampling is the estima-

tion of the sample size. There are several sample

size estimation techniques in the literature. However,

in this study, we mainly focused on the techniques

specialized on association mining (Zaki et al., 1997;

Chakaravarthy et al., 2009; Toivonen et al., 1996;

Riondato and Upfal, 2012).

Association mining can be realized in two steps,

namely frequent itemset (FI) discovery and associa-

tion rule (AR) generation (Agrawal et al., 1993). A

randomly selected sample contains statistical errors,

particularly in support and conﬁdence calculations.

Error is calculated at either FI discovery step or AR

generation step. Moreover, they are compared by the

corresponding value of the universe either absolutely

or relatively. The classiﬁcation of the sampling size

estimation techniques depends on the type of the error

and the step where the error has emerged (Riondato

and Upfal, 2012).

Table 1: Sampling size estimation techniques.

Technique Type Formula

Zaki FI

abs

−2ln(1−γ)

Θδ

Toivonen FI

abs

2ε

Chakaravarthy FI

abs

(1−ε)ε

(∆ + 5 + ln

(1−ε)Θδ

)

Chakaravarthy AR

abs

(1−ε)ε

(∆ + 5 + ln

(1−ε)Θδ

)

Riondato FI

abs

(v + ln

)

Riondato FI

rel

4(2+ε)c

(2−ε)Θ

(vln

2+ε

Θ(2−ε)

+ ln

)

Riondato AR

abs

(vln

+ ln

)

Riondato AR

rel

(vln

+ ln

)

For the sake of brevity, let us give parameters used

in the techniques;

ε: upper bound of absolute/relative error,

δ: failure probability in FI discovery/AR genera-

tion step,

Θ: minimum support of FI,

γ: minimum conﬁdence of AR,

∆: maximum transaction length,

η: function of Θ, γ and ε,

p: function of η and Θ,

v: d-index of the universe,

c: constant.

Detailed explanation about these parameters and

proofs of approximations can be found in the studies

(Zaki et al., 1997; Chakaravarthy et al., 2009; Toivo-

nen et al., 1996; Riondato and Upfal, 2012; L

ofﬂer

and Phillips, 2009; Har-Peled and Sharir, 2011; Man-

nila et al., 1994). Studied sample size estimation tech-

niques according to their classiﬁcation are as follows;

2.2.1 FI - Absolute Error

The techniques in this group aim to control the error

in support values occurred at FI discovery step. The

absolute error is

error

abs

= |supp

− supp

|, (4)

where supp

and supp

denote the support of a given

itemset calculated from the sample and the universe,

respectively. These techniques are labeled as FI

abs

Table 1.

Zaki, Toivonen, Chakaravarthy and Riondato

techniques utilize Chernoff bounds theorem for sam-

ple size estimation. Each technique considers a differ-

ent random variable that is generated from the dataset.

Zaki concentrates on the expected support of frequent

itemsets, whereas Toivonen deals with the absolute

support error of the frequent itemsets.

Both Chakaravarthy and Riondato study ε-close

approximation of the frequent itemsets using absolute

support errors. Chakaravarthy considers the longest

transaction length in the universe, whereas Riondato

exploits the d-index of the universe. The d-index

relies on the VC dimension of the dataset, which

gives information about the transactions in the uni-

verse (Vapnik and Chervonenkis, 1971). Detailed

proofs can be found in the studies of (Zaki et al., 1997;

Chakaravarthy et al., 2009; Toivonen et al., 1996;

Riondato and Upfal, 2012).

2.2.2 FI - Relative Error

The technique in this group aims to control the error

in support values occurred at FI discovery step. The

relative error is

error

rel

|supp

− supp

|supp

(5)

Comparison of Sampling Size Estimation Techniques for Association Rule Mining

197

where supp

and supp

denote the support of a given

itemset calculated from the sample and the universe,

respectively. These techniques are labeled as FI

rel

Table 1.

Riondato technique uses Chernoff bounds theo-

rem for sample size estimation. The d-index of the

universe is exploited for a relative ε-close approxi-

mation of the frequent itemsets. The relative errors

occurred in the approximations are considered in the

computations. Detailed proof can be found in the

study of (Riondato and Upfal, 2012).

2.2.3 AR - Absolute Error

The technique in this group aim to control the error

in conﬁdence values occurred at AR generation step.

The absolute error is

error

abs

= |con f

− con f

| (6)

where con f

and con f

denote the conﬁdence of a

given rule calculated from the sample and the uni-

verse, respectively. These techniques are labeled as

abs

in Table 1.

Chernoff bounds theorem on absolute conﬁdence

errors of an ε-close approximation of the association

rules is executed by both of the techniques. Chakar-

avarthy considers the longest transaction length in the

universe, whereas Riondato exploits d-index of the

universe. η and p parameters are functions of Θ, γ and

absolute ε. Detailed proofs, the deﬁnitions of η and

p parameters can be found in the studies of (Chakar-

avarthy et al., 2009; Riondato and Upfal, 2012).

2.2.4 AR - Relative Error

The technique in this group aims to control the error

in conﬁdence values occurred at AR generation step.

The relative error is

error

rel

|con f

− con f

|con f

(7)

where con f

and con f

denote the conﬁdence of a

given rule calculated from the sample and the uni-

verse, respectively. These techniques are labeled as

rel

in Table 1.

Riondato technique utilizes Chernoff bounds the-

orem. Relative ε-close approximation of association

rules by exploiting d-index of the universe is studied.

The d-index relies on the VC dimension of the dataset,

which gives information about the transactions in the

universe (Vapnik and Chervonenkis, 1971). η and p

parameters are functions of Θ, γ and relative ε. The

relative errors occurred in the approximations are con-

sidered in the computations. Detailed proof and the

deﬁnitions of η and p parameters can be found in the

study of (Riondato and Upfal, 2012).

3 REPRESENTATIVENESS TESTS

Application of the sampling method and the sampling

size estimation technique result into a statistical sam-

ple of the universe. The assumption under utilization

of sampling in association mining is that, the sam-

ple is similar to universe in terms of the associations

(Zaki et al., 1997; Chakaravarthy et al., 2009; Toivo-

nen et al., 1996; Riondato and Upfal, 2012). Thus,

the sample can be mined for associations instead of

the universe.

Statistical hypothesis tests are used in order to de-

termine the probability that a given hypothesis is true.

In this paper, hypothesis tests are realized in order to

prove the dissimilarity between the sample and the

universe. These tests contain two hypotheses, which

are opposite to each other, namely null hypothesis and

alternative hypothesis. The null hypothesis is

: s

= U

∀i, (8)

which assumes the sample s and the universe U have

same frequencies for all categories. The alternative

hypothesis is

: s

6= U

∃i, (9)

which assumes the sample s and the universe U differ

in some frequencies for some categories. The assess-

ment of the truth of H

is realized with tests, such as

and Kolmogorov-Smirnov (K-S). Each test outputs

a test statistics. These statistics are converted into p

values in order to compare with the acceptable signiﬁ-

cance level α. If p < α, then H

is rejected at the given

level of signiﬁcance. Otherwise, test has no result,

i.e. there is no sufﬁcient evidence to prove/disprove

the similarity between the sample and the universe.

For this work, the signiﬁcance level is assumed to be

α = 0.05. The computed p values are compared with

0.05, in order to reject the null hypothesis.

Statistics are computed from a different point of

view in both of the tests. χ

test computes the average

deviance in the frequencies, whereas K-S test com-

putes the maximum deviance in the cumulative fre-

quencies. χ

test is sensitive to sample size and small

frequencies (Agresti, 1996). In other words, a small

sample with small frequencies result into bias in test

results. In K-S test, type II error rates are greater than

test (Durbin, 1973). Thus, there is a tendency to-

wards the rejection of the null hypothesis. Therefore,

the p values calculated from each test, may result into

different values. Due to these drawbacks, both of the

tests are conducted for comparison of the results.

KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval

198

4 EXPERIMENTATIONS

Tests are conducted on real customer-product owner-

ship data. Original bank dataset contains 143 prod-

ucts, that are classiﬁed into 10 product groups ac-

cording to the hierarchy deﬁned by the bank. Aim-

ing to speed up the test phase, product groups are

mined for associations instead of all products. Uni-

verse dataset contains 1,048,575 customers and prod-

uct group ownership statuses. Rows and columns rep-

resent customers and product groups, respectively.

Sample size estimation technique parameters are

taken as accuracy ε = 0.04, failure probability δ =

0.07, minimum support Θ = 0.02 and minimum con-

ﬁdence γ = {0.06, 0.1, 0.14}. Accuracy and fail-

ure probability are chosen according to the study

of Riondato, whereas minimum support is chosen

based on the universe dataset (Riondato and Upfal,

2012). Minimum conﬁdence varies as in the study of

Riondato for ﬁxed accuracy, failure probability and

minimum support (Riondato and Upfal, 2012). Same

minimum support and minimum conﬁdence values

are used for association mining process.

Simple random sampling and stratiﬁed random

sampling methods were adopted. Simple random

sampling draws each transaction with equal probabil-

ities. In stratiﬁed random sampling, 4 categories are

created. Two most common product groups among

customers are discovered, say A and B. Combination

of these two product groups are built, namely only A

owners, only B owners, both A and B owners and none

of A and B owners. The ratios of these categories are

preserved in the samples as in the universe.

R programming language is used for code devel-

opment. The following steps are followed during test

phase;

1. Estimation of sample sizes,

2. If the technique estimates a smaller size than the

universe size, then 10 different samples are cre-

ated using simple random sampling and stratiﬁed

random sampling methods for each technique,

3. Analysis of χ

and K-S tests for representative-

ness of the samples,

4. Discovery of FIs and generation of ARs from uni-

verse and sample by using arules package of R

programming language,

5. Comparison of results and calculation of error val-

ues,

6. Comparison of elapsed time during AR genera-

tion from universe with total time spent on sample

creation and AR generation from sample.

4.1 Sample Size

Using techniques presented in Section 2.2, we have

calculated sample sizes. Table 2 shows sample size

estimations for varying γ values which is the main

parameter impacting the sample size. Sample sizes

estimated by Toivonen, Chakaravarthy FI

abs

, Chakar-

avarthy AR

abs

, Riondato FI

abs

ve Riondato FI

rel

not differ with γ values, since γ is not taken as a pa-

rameter in these formulae.

Table 2: Sample size estimations varying with minimum

conﬁdence.

Technique Type γ =

0.06

γ =

0.10

γ =

0.14

Zaki FI

abs

3867 6585 9426

Toivonen FI

abs

1047 1047 1047

Chakaravarthy FI

abs

≈15M ≈15M ≈15M

Riondato FI

abs

9574 9574 9574

Riondato FI

rel

≈15M ≈15M ≈15M

Chakaravarthy AR

abs

≈30M ≈30M ≈30M

Riondato AR

abs

15057 47005 96859

Riondato AR

rel

≈5M ≈5M ≈5M

Chakaravarthy FI

abs

, Chakaravarthy AR

abs

Riondato FI

rel

and Riondato AR

rel

techniques offer

bigger sizes than universe size (1048575). As one

of our main concern is to ﬁnd the optimal sample

size, a sample with a greater size than the actual

universe is an undesired outcome. Hence the tech-

niques stated above have been left out of further

investigations. Table 2 presents the results of sample

size estimations.

4.2 p Value

For each sample size presented in Table 2 that are

smaller than the universe size, we have created sam-

ples using simple random sampling and stratiﬁed ran-

dom sampling methods. We have drawn 10 different

samples in order to minimize error arising from ran-

domness of sampling methods.

We adopted p value for testing null hypothesis.

We determined α = 0.05 as signiﬁcance level of the

tests. If p values are less than the signiﬁcance level,

null hypothesis, i.e. the sample is similar to the uni-

verse, is rejected.

We present average p values calculated from χ

and K-S tests in Table 3 for the samples obtained from

simple random sampling and Table 4 summarizes the

same test results for the samples obtained from strati-

ﬁed random sampling.

The major interpretation of p values to understand

the representativeness of a sample is that, the p values

are greater than the signiﬁcance level. Thus, there is

Comparison of Sampling Size Estimation Techniques for Association Rule Mining

199

Table 3: Average p values for simple random samples computed from χ

and K-S tests.

Technique Type γ = 0.06 γ = 0.10 γ = 0.14

K-S χ

K-S

Zaki FI

abs

0.409 0.364 0.605 0.636 0.496 0.313

Toivonen FI

abs

0.429 0.365 0.643 0.408 0.589 0.339

Riondato FI

abs

0.437 0.583 0.531 0.670 0.458 0.493

Riondato AR

abs

0.425 0.328 0.558 0.499 0.612 0.575

Table 4: Average p values for stratiﬁed random samples computed from χ

and K-S tests.

Technique Type γ = 0.06 γ = 0.10 γ = 0.14

K-S χ

K-S

Zaki FI

abs

0.606 0.417 0.697 0.525 0.576 0.456

Toivonen FI

abs

0.619 0.475 0.501 0.525 0.477 0.264

Riondato FI

abs

0.624 0.504 0.710 0.428 0.505 0.640

Riondato AR

abs

0.618 0.451 0.692 0.649 0.577 0.481

no sufﬁcient evidence to disprove statistical similarity

between the universe and the samples.

p values obtained by χ

and K-S tests are not

equivalent because of the reasons explained in Section

3. Besides, we could not observe any proportionality

between sample sizes and p values. For the samples

with constant sizes but with varying γ values, the ap-

plication of the Toivonen technique has provided un-

stable p values.

We have tested both simple random sampling and

stratiﬁed random sampling methods under different

techniques but we cannot observe any signiﬁcant dif-

ference between results.

4.3 Absolute Support and Conﬁdence

Errors

Discovery of FIs and generation of ARs are real-

ized by Apriori algorithm. The absolute errors in

support and conﬁdence values are measured for FIs

and ARs respectively. Zaki and Toivonen techniques

miss some FIs and ARs that exist in the universe.

Corresponding p values of these techniques did not

give sufﬁcient information to disprove the similarity.

However, using absolute errors, we noticed that these

two sample size estimation techniques do not give sat-

isfactory results. The ineffectiveness of these meth-

ods depends on their small sample sizes.

Since loss in association rules is undesirable, these

two techniques are interpreted as ineligible for sam-

pling and they are not subject to further testing. Miss-

ing support and conﬁdence values are taken as 0. Av-

erage support and conﬁdence errors for simple ran-

dom samples (respectively for stratiﬁed random sam-

ples) are shown in Figure 1 (respectively in Figure 2)

for varying minimum conﬁdence. As shown in the

ﬁgures, Riondato’s techniques present better results

than other techniques in terms of support and conﬁ-

dence errors.

In compliance with our expectations, the conﬁ-

dence errors are high whenever support error is high.

In addition, there is a relation between the sample

size and the errors. The bigger the sample sizes, the

smaller the errors (See Table 2 for sample size varia-

tion).

Comparing the results of simple random sampling

and stratiﬁed random sampling methods, we did not

observe any remarkable difference.

Figure 1: Average support and conﬁdence errors for simple

random samples for varying minimum conﬁdence γ.

KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval

200

Figure 2: Average support and conﬁdence errors for strati-

ﬁed random samples for varying minimum conﬁdence γ.

4.4 Time Consumption

We present time consumptions for both universe and

sample until the end of AR generation in Figure 3 and

Figure 4. Tests are conducted on a PC with 3.2 G Hz

i5 processors and 8 GB RAM.

For universe, only AR generation time is given,

whereas for sampling techniques, average total time

for sample size estimation, simple random sampling

or stratiﬁed random sampling and AR generation is

given. As expected, for all γ values, sampling tech-

niques performed at least approximately six times bet-

ter than universe. We anticipate that time performance

will be more visible when 143 products are included

in the sampling process rather than just 10 groups of

product.

Figure 3: Time consumptions (in seconds) until AR gener-

ation for simple random samples.

Figure 4: Time consumptions (in seconds) until AR gener-

ation for stratiﬁed random samples.

5 CONCLUSIONS AND FUTURE

WORKS

We targeted creating a representative small size sam-

ple out of universe and mining it for association rule

retrieval. The initiative for sampling is to minimize

memory and time consumptions. For this purpose,

sampling size estimation techniques specialized on

association mining, sampling methods and represen-

tativeness tests are investigated and applied in this

study. Samples are created by utilizing simple ran-

dom sampling and stratiﬁed random sampling meth-

ods to crosscheck the results. For each technique sat-

isfying size condition, 10 samples are created. The ra-

tionale behind multiple samples for a given technique

is to minimize noise introduced by random sampling

methods. Techniques are tested with varying mini-

mum conﬁdence values. The choice of parameter val-

ues is based on the study of Riondato. The very ﬁrst

interpretation about techniques is that not all of them

are applicable for any size of universe. We observed

3 different indicators in order to compare the results.

First, we examined p value as an a-priori indica-

tor of representativeness. According to p values, we

could not reject any sample because of representative-

ness. However, when we compare FIs and ARs from

the universe and the sample, we realized that some

techniques miss some FIs and ARs, leading to infor-

mation loss. For instance, sample sizes calculated by

Toivonen technique are not rejected because of rep-

resentativeness according to p values for γ = 0.06.

However, it misses some FIs and ARs. Hence, we

conclude that traditional statistical methods are not

suitable tools for testing representativeness of sam-

ples created for association mining. One of our con-

tributions is the identiﬁcation of the unavailability of

the statistical tests to check the representativeness of

sampling for association mining.

In addition, observations in absolute errors in con-

ﬁdence and support helped us to identify sample size

Comparison of Sampling Size Estimation Techniques for Association Rule Mining

201

estimation techniques leading to loss of FIs and ARs.

We noticed that use of these techniques for associa-

tion mining is not convenient.

Examining the absolute errors, we veriﬁed that the

bigger the sample size, the smaller the absolute errors.

Riondato FI

abs

and AR

abs

return the smallest absolute

errors due to their high sample size. We could not

ﬁnd any threshold of acceptance for errors identiﬁed

in the studies of this domain. In future works, we aim

to determine this threshold.

Besides, time elapsed during AR generation from

the universe is compared with total time elapsed dur-

ing sample size estimation, creating samples with

simple random sampling or stratiﬁed random sam-

pling method and AR generation from the sample.

Each of the techniques performed better than universe

in terms of time consumption. According to the abso-

lute errors, Riondato FI

abs

and Riondato AR

abs

tech-

niques are the best performers. When smaller sam-

ple size and less time consumption criteria are taken

in concern, Riondato FI

abs

is the leading sample size

estimation technique. Among several different sam-

ple size estimation techniques, we identiﬁed Riondato

abs

to be the most suitable technique for our retail

banking data.

Dataset contains retail bank customers and their

product group ownership information. Rather than

the individual products owned by the customers, the

groups of these products are taken into consideration.

The main reason for this decision is to eliminate spar-

sity on the dataset and speed up the test phase. Use

of product groups has led to small time consump-

tions even on the universe. Even though duration

gain seems to be in the order of seconds, bigger gains

can be obtained if larger product sets are tested. For

next studies, dataset will be expanded and robustness

check will be done with an alternative dataset.

Moreover, systematic, cluster and multistage sam-

pling methods can be applied during construction of

association rule mining data. For instance, the cus-

tomers which will be subjects of ARM can be drawn

according to their clusters (e.g. geographical areas).

Our research focuses on the association rule mining

data (including binary values). Extraction of this data

from customers’ dataset will be examined in further

studies.

REFERENCES

Agrawal, R., Imieli

nski, T., and Swami, A. (1993). Min-

ing association rules between sets of items in large

databases. In ACM SIGMOD Record, volume 22,

pages 207–216. ACM.

Agresti, A. (1996). An introduction to categorical data

analysis, volume 135. Wiley New York.

Chakaravarthy, V. T., Pandit, V., and Sabharwal, Y. (2009).

Analysis of sampling techniques for association rule

mining. In Proceedings of the 12th international con-

ference on database theory, pages 276–283. ACM.

Durbin, J. (1973). Distribution theory for tests based on the

sample distribution function, volume 9. Siam.

Har-Peled, S. and Sharir, M. (2011). Relative (p, ε)-

approximations in geometry. Discrete & Computa-

tional Geometry, 45(3):462–496.

Hidber, C. (1999). Online association rule mining, vol-

ume 28. ACM.

Hipp, J., G

untzer, U., and Nakhaeizadeh, G. (2000). Algo-

rithms for association rule mining—a general survey

and comparison. ACM sigkdd explorations newsletter,

2(1):58–64.

ofﬂer, M. and Phillips, J. M. (2009). Shape ﬁtting on point

sets with probability distributions. In Algorithms-ESA

2009, pages 313–324. Springer.

Mannila, H., Toivonen, H., and Verkamo, A. I. (1994). E

cient algorithms for discovering association rules. In

KDD-94: AAAI workshop on Knowledge Discovery in

Databases, pages 181–192.

Pei, J., Han, J., Lu†, H., Nishio, S., Tang, S., and Yang, D.

(2007). H-mine: Fast and space-preserving frequent

pattern mining in large databases. IIE Transactions,

39(6):593–605.

Pei, J., Han, J., Mao, R., et al. (2000). Closet: An efﬁ-

cient algorithm for mining frequent closed itemsets. In

ACM SIGMOD workshop on research issues in data

mining and knowledge discovery, volume 4, pages 21–

30.

Riondato, M. and Upfal, E. (2012). Efﬁcient discovery of

association rules and frequent itemsets through sam-

pling with tight performance guarantees. In Machine

Learning and Knowledge Discovery in Databases,

pages 25–41. Springer.

Toivonen, H. et al. (1996). Sampling large databases for

association rules. In VLDB, volume 96, pages 134–

145.

Vapnik, V. N. and Chervonenkis, A. Y. (1971). On the uni-

form convergence of relative frequencies of events to

their probabilities. Theory of Probability & Its Appli-

cations, 16(2):264–280.

Zaki, M. J. and Hsiao, C.-J. (2002). Charm: An efﬁcient al-

gorithm for closed itemset mining. In SDM, volume 2,

pages 457–473. SIAM.

Zaki, M. J., Parthasarathy, S., Li, W., and Ogihara, M.

(1997). Evaluation of sampling for data mining of as-

sociation rules. In Research Issues in Data Engineer-

ing, 1997. Proceedings. Seventh International Work-

shop on, pages 42–50. IEEE.

Zhang, H., Zhao, Y., Cao, L., and Zhang, C. (2008). Com-

bined association rule mining. In Advances in Knowl-

edge Discovery and Data Mining, pages 1069–1074.

Springer.

KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval

202