Aerodynamical Resistance in Cycling
CFD Simulations and Comparison with Experiments
Luca Oggiano, Live Spurkland, Lars Sætran and Lars Morten Bardal
Norwegian University Of Science and Technology, Deparment of Energy and Process Engineering,
K. Hejes Vei 2b, 7042 Trondheim, Norway
Keywords: Aerodynamics, CFD, Wind Tunnel Testing, Cycling.
Abstract: The present work shows a comparison between computational fluid dynamics (CFD) simulations obtained
using the Unsteady Reynolds Averaged Navier-Stokes solver STARCCM+ from CD-Adapco and
experiments carried out in the subsonic wind tunnel at NTNU. The models tested in the wind tunnel (a
mannequin and real cyclist in static position) were 3D scanned using a 3D scanner, consisting 48 single-lens
reflex cameras surrounding the object in three heights (low/ground-midi-above). A hybrid meshing
technique was used in order to discretize the surface and the volume. Polyhedral cells were used on the
model surface and in the near volume while a structured grid was used in the rest of the domain. An
unsdeady RANS approach was used and the turbulence was modelled using the Menter implementation of
the k-ω model. No wall functions were used and the boundary layer was fully resolved. The first part of the
paper focuses on the mannequin while in the second part the comparison between the experimental results
and simulation on the real cyclist are presented. An overall good agreement between the simulations and the
experiments was found proving that CFD could be a complementary tool to wind tunnel testing.
1 INTRODUCTION
The aerodynamic drag is the main opposing force
that cyclists need to overcome and it counts up 90%
((De Groot et al., 1995, Di Prampero, 2000; Oggiano
et al., 2008)) of the total resisting forces experienced
by a cyclist at racing speeds. The cyclist itself counts
up to 70% of the total drag while the remaining 30%
is due to the bicycle (Blocken et al., 2013;
Underwood, 2012; Underwood and Jermy, 2011;
Oggiano et al., 2008) and this leads to the fact that
even small reductions could give large
improvements in terms of performances.
The aerodynamic drag generated by the cyclist is
directly linked to a number of parameters.
Expressing the drag as
(1)
It can be immediately noticed that, for a given
location where the air density [kg/m
3
] is assumed
to be constant, the drag is proportional to the square
of the wind speed U [m/s], to the frontal area A [m
2
]
and to the non-dimensional drag coefficient C
D
[-].
Being the frontal area measurements often not
reliable (Debraux et al., 2012), a combined
parameter called arag area C
D
A is used to quantify
the effectiveness of a cycling posture.
In order optimize their posture with the main goal
to reduce the drag area (and thus the drag),
experimental tests became common amongst elite
cyclists. Different methods of assessment of
aerodynamic drag (wind tunnel tests, linear
regression analysis models, traction resistance
measurement methods and deceleration methods) are
currently used and each of them has pros and cons
(Debraux et al., 2012).
Beside experimental methods, Computational
Fludi Dynamics (CFD) simulations became a viable
option due the increase in computational power
available and to the possibility to parallelize the
simulations splitting large meshes into smaller
domains. Encouraging results from CFD simulations
applied to cycling can be found in (Hanna, 2002;
Defraeye et al., 2010a; Defraeye et al., 2010b;
Defraeye et al., 2011; Lukes et al., 2002; Blocken et
al., 2013)
and while applications in other sports have
been carried out by a number of other authors
(Lecrivain et al., 2008; Minetti et al., 2009; Zaïdi et
al., 2010)
.
CFD simulations present some pros and some
cons if compared with wind tunnel tests. While wind
F
D
0.5c
D
U
2
A
Oggiano, L., Bardal, L., Sætran, L. and Spurkland, L..
Aerodynamical Resistance in Cycling - CFD Simulations and Comparison with Experiments.
In Proceedings of the 3rd International Congress on Sport Sciences Research and Technology Support (icSPORTS 2015), pages 183-189
ISBN: 978-989-758-159-5
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
183
tunnel tests are able to provide only the total drag
force acting on the model, CFD can provide drag
information on individual body segments or bicycle
components, increasing the insight in drag reduction
mechanisms and allowing local modifications.
Furthermore, CFD simulations are able to provide
instantaneous field data while wind tunnel tests are
not. On the other hand, the main disadvantage of
CFD versus wind tunnel tests is that moving athletes
are extremely complex to simulate and thus
simulations are confined to static models. The other
main issue is that, in order to reduce the
computational cost of the simulations, turbulence
has to be modelled and cannot be fully resolved.
This simplification has two main drawbacks: the
separation lines on the model will be placed
considering the flow around the model fully
turbulent (not always true in reality) and, even with
the use of surface roughness and transition models,
drag reduction techniques (Oggiano and Sætran,
2012; Oggiano et al., 2009; Brownlie, 1992;
Brownlie et al., 1987; Brownlie et al., 2009) cannot
be simulated or directly implemented in the
simulation.
The present work aims to validate CFD
simulations towards experiments proving the
effectiveness of CFD as a complementary rather
than a substitute tool to wind tunnel tests.
2 EXPERIMENTAL SETUP
Testing of the mannequin models and cyclist were
conducted in the large wind tunnel at NTNU. The
wind tunnel is equipped with a 220KW fan engine,
has a maximum speed of 30m/s and the testing
section is 2,7x1,8x12,5 meters. A pitot tube and a
thermocouple type K was used to monitor the wind
speed and temperature respectively. The drag was
measured with a Schenck six component force
balance where only the axis of the drag direction
was used. The drag force was calculated from the
measured CdA values and normalized
2.1 Mannequin Model
The test on the mannequin model were conducted on
five velocities ranging from 9.53 to 18.2 m/s
(corresponding to 35 to 72,5 km/h).
The mannequin model used for the test was a
full-scale upper body including head and upper arms
belonging to a model of height 170 cm and weight
70 kg. Its position was adjusted to imitate that of a
cyclist in the drop bars. The forearms were removed
to reduce the amount of uncertainty and helmets
were not included in the test. The model was tested
with a number of jerseys with different surface
pattern and without jersey with different rough
patches applied to the shoulder. Its position was
adjusted to resemble the dropped position of a
cyclist.
2.2 Mannequin Model
The full scale test on a cyclist was carried out at a
single wind speed (13.09m/s). A regular road bike
was placed on a training roller so that the tires were
not touching the wind tunnel floor and the roller was
connected to the force plate. The front wheel was
stationary and supported by a custom-made wheel
stand. The cyclist was positioned in drop positon
with live pictures from a side camera projected in
front of the rider showing their position
superimposed with an outline of her initial position
to keep it as consequent as possible.
3 NUMERICAL SETUP
3.1 Computational Domain and
Geometry
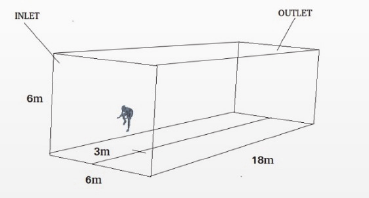
Figure 1: Numerical wind tunnel.
The numerical simulations were set up for a
cyclist without bicycle setup and for a mannequin
without support setup. The bike modelling was
discarded in order to reduce the mesh size and thus
the computational cost of the simulation. However,
due to this approach, the interaction between the
bike and the cyclist was discarded and simplified.
No roughness was added to the model while it has
been previously shown that roughness could be a
key factor and dramatically affect the drag
(Brownlie, 1992; Brownlie et al., 1987; Brownlie et
al., 2009). The digital models for mannequin and
cyclist were obtained using a high-resolution 3D
laser scanning. The cyclist and mannequin digital
models were placed in a numerical wind tunnel. A
icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support
184

preliminary study on the domain size was carried out
in order to avoid backflow that could affect the
simulation. The domain shape and size is specified
in Figure 1.
3.2 Mesh and Grid Sensitivity
Figure 2: Mesh refinement technique a) farfield area
(structured mesh). b) wake area (structured mesh). c) Near
model area (unstructured polyhedral mesh).
A hybrid meshing approach was used to mesh
the cyclist and the wind tunnel. A polyhedral
meshing approach was used to discretize the models
surface while a structured hexaedra approach was
used for the rest of the domain. The polyhedral
meshing technique allows smoother surfaces using
fewer cells than triangular and tetrahedral meshing
reducing computational cost. The boundary layer
was resolved using an extruded mesh consisting of
10 layers. A growing ratio of 1.25 was used and the
nearest cell to the surface was placed in order to
ensure a non-dimensional distance from the wall
y+<5, (where y+ is the distance y to the wall, non
dimentionalized with the friction velocity u
τ
and
kinematic viscosity ν). This is needed in order to
correctly resolve the viscous boundary layer in flows
with high Re numbers. The models were contained
in a near volume block of L x W x H = 2 x 2 x 1.5m
meshed with polyhedral meshing. A structured grid
with a greed refinement in the wake area was used to
model the rest of the domain. The near-model
volume was patched with the rest of the domain
using the overset mesh technique implemented in
STARCCM+. The overlap region between the near
model mesh and the domain mesh was chosen to me
10cm. Three different surface meshes were used in a
preliminary test in order to ensure a grid
independent solution: a reference mesh consisting of
6.1million cells approximately, a coarse grid
consisting of 3.1million approximately and a fine
grid consisting of 12million cells approximately.
3.3 Boundary Conditions
Standard boundary conditions suggested in the
STARCCM+ guide were used for the current
simulation (Cd-ADAPCO, 2015). A uniform flow
inlet was used at the inlet. For the oulet, assuming
the outlet pressure known and equal to the
atmospheric pressure, and being the exact details of
the flow distribution unknown a pressure oulet
boundary condition was used. Symmetrical
boundary conditions were used in sides, top and
bottom of the domain assuming that on the two sides
of the boundary, same physical processes exist. With
symmetrical boundary condition, all the variables
have same value and gradients at the same distance
from the boundary and no flow across boundary and
no scalar flux across boundary. Even if this
simplification could be considered acceptable, one
has to be aware that the numerical domain is
simplified with the real wind tunnel. In particular,
this assumption leads to the fact that friction at the
walls, with the direct consequence of boundary layer
growth, is neglected and blockage effects are not
considered (Chung, 2002). The model surface was
modelled as a smooth wall surface with no slip
conditions.
3.4 Solver Settings and Turbulence
Modelling
The URANS turbulent flow solver implemented in
STARCCM+ was used for the simulations and the k-
ω Menter SST turbulence model was used for the
simulations. A preliminary comparative study using
the standard one equation Spalart Allmaras (SA)
(Spalart, 2000) and the two equations k-ɛ model
(Launder and Sharma, 1974) and the k-ω Menter
SST (Menter, 1994) models was carried out and no
noticeable differences between the use of the three
models were found. Even if it is common knowledge
that that no single turbulence model can be
considered superior for all classes of problems and
thus the choice of turbulence model often depends
on considerations such as the physics embedded in
the problem, the level of accuracy required and the
available computational resources, the choice was
made based on comparisons carried out by other
authors. The SA does not accurately compute fields
that exhibit shear flow, separated flow, or decaying
turbulence. Its advantage is that it is quite stable and
shows good convergence. K-ɛ does not accurately
compute flow fields with adverse pressure gradients,
strong curvature to the flow, or jet flow. The k- ω
Menter SST model does not use wall functions and
tends to be most accurate when solving the flow near
the wall. Furthermore, SST model also enables to
capture the vortex structures developing in the wake
region. For this reason, since large separation and
Aerodynamical Resistance in Cycling - CFD Simulations and Comparison with Experiments
185
vorticity is expected in the present test, the k-ω SST
model was chosen (Zaïdi et al., 2010; Wilcox,
2006).
4 RESULTS AND DISCUSSION
4.1 Mannequin Models
The digital scanned model was positioned in the
numerical wind tunnel in order to correctly
reproduce the experiments position. The same
simulation was carried out at six different wind
speeds in order correctly replicate the wind tunnel
experiments and verify if the velocity could
influence the drag area.
4.1.1 Validation Against Experiments
(Jersey on)
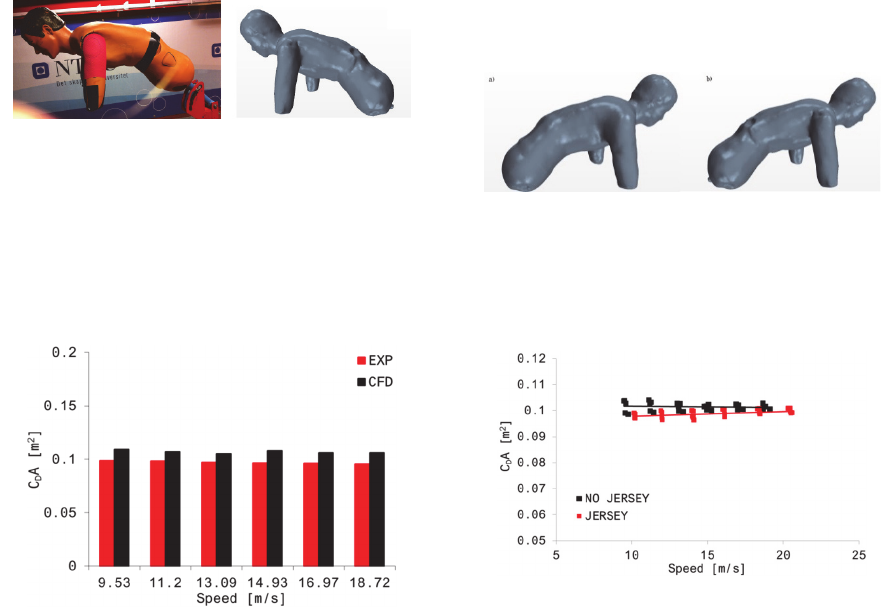
Figure 3: Mannequin model in the wind tunnel (left) and
3D laser scanned model (right).
Table 1: Comparison between experiments and
simulations for the mannequin with jersey on.
Figure 4: C
D
A values at different speeds for the
mannequin with the jersey on for experiments (red) and
simulations (black).
The results show that CFD simulations
consistently match experiments at different wind
speeds with an error between simulations and
experiments in the order of 10% which can
considered to be a good agreement (Blocken et al.,
2013). The results clearly show that the C
D
A
parameter is constant at different wind speeds
allowing further simulations to limited to a single
speed.
4.1.2 Effect of Jersey on the Surface
Two different configurations of the model were
simulated (with and without jersey) in order to
evaluate how the jersey could influence the overall
drag. The test was carried out at 14.93m/s with the
assumption that the drag coefficient would be
constant at different wind speeds. Grooves and
irregularities due to joints and mannequin
construction were present on the model without
jersey while these surface irregularities were either
covered or smoothed in the scanned model with the
jersey on (see Figure 5). In particular bumps and
imperfections on the back and shoulder area can be
seen in the Figure 5b while these imperfections are
smoothed out in the model shown in Figure 5a
Figure 5: 3D scanned model a) model with jersey on. b)
model without jersey.
The measured drag from the mannequin without jersey
resulted to be higher than the measured drag from the
mannequin with jersey on Figure 6.
Figure 6: Experimental results from the mannequin test
with and without jersey.
The comparison between CFD and experiments
presented in Figure 7 shows the same trend seen in
Figure 6 and the main conclusion is that placing a
jersey on the model surface affects the flow around
reduces drag.
Speed [m/s] 9.53 11.2 13.09 14.93 16.97 18.72
CFD 0.109 0.107 0.105 0.108 0.106 0.106
[m
2
] EXP 0.098 0.098 0.097 0.096 0.096 0.095
Error [%] 10.9 8.8 8.4 11.9 10.4 11.3
C
D
A
icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support
186

Figure 7: C
D
A values from experiments (red) and
simulations (black) for the mannequin model with and
without jersey at 14.93m/s.
The irregular surface on the plain model creates
low pressure zones that induce separation and
recirculation of the flow with a consequent increase
of pressure drag (Figure 8). In particular, it can be
seen in in Figure 8b the wake area is larger than in
Figure 8a. A high pressure area on the side of the
model without jersey is also present while the same
effect is not visible on the model with the jersey on.
Figure 8: Pressure contour plots on a) the mannequin with
jersey on and b) mannequin without jersey.
The same findings can be seen when plotting the
friction lines on the model. A recirculation area on
the side of the model can be seen. This recirculation
area is generated by the groove in the shoulder
region where the arm is attached to the torso. From
Figure 9 it can also be seen that the flow on the arm
separates differently on the model with jersey and on
the model without jersey.
Figure 9: Friciton lines on the model with jersey (a,c) and
without jersey (b,d).
Similar conclusions come also from figure 10
where the vorticity field around the model is
represented for visualization purposes. In the model
with no jersey Figure 10b, the groove in the shoulder
joint creates a vortex that develops and reattaches on
the side of the model while the irregularities in the
back induce separation.
Figure 10: Vorticity field around the mannequin model. a)
with jersey b) without jersey.
4.2 Cyclist
4.2.1 Validation Against Experiments
(Dropped Position)
Experiments were available only for the cyclist in
dropped position. The drag of the bare athlete with
no bike was obtained subtracting the drag measured
for the bare bike from the drag measurements from
the bike+cyclist test. While the experiments were
carried out at three different wind speeds, a single
CFD simulation at 13.09 m/s was carried out
assuming the C
D
A from CFD to be independent
from the wind speed.
The results from the CFD simulation match the
experiments with an error of 10% and the simulated
drag area C
D
A is consistently higher than the
measured one. The over prediction of the
aerodynamic drag is a known problem in CFD
simulations and it is directly linked to the turbulence
modelling (Blocken et al., 2013). The standard
turbulence models are in fact not able to correctly
simulate the vortices in the recirculation regions and
they often tend to keep the large structures without
correctly resolving the smaller structures that are
responsible of the vortex breaking mechanism,
leading to an over prediction of the total drag.
Figure 11: C
D
A values for the cyclist model from
simulations (black) and experiments (red).
Aerodynamical Resistance in Cycling - CFD Simulations and Comparison with Experiments
187

Figure 12 illustrates the vorticity field around the
cyclist and the pressure field on the cyclist. The
interaction between the different body parts can be
seen in Figure 12a where the vortices generated by
the arms directly interact with the athlete trunk.
Figure 12b gives an overview of the area where
separation might occur. The low pressure areas (blue
color) are areas where the flow is detached. Large
vortices are usually generated from these areas
leading to an increase in total drag. Major attention
to these areas is then important when designing a
low drag suit.
Figure 12: Vorticity field around the full model. And
pressure contour plots on the model.
5 CONCLUSIONS
CFD simulations proved to be a useful tool and the
results consistently matched the experimental results
with an over prediction estimated to be around 10%.
If on one side experiments are still needed,
especially for surface modifications and dynamic
testing, CFD could give a much better insight of the
pressure and force distribution on the body. CFD
could then be a good complementary tool to use in
parallel with wind tunnel testing
REFERENCES
Blocken, B., Defraeye, T., Koninckx, E., Carmeliet, J. &
Hespel, P. 2013. Cfd simulations of the aerodynamic
drag of two drafting cyclists. Computers & Fluids, 71,
435–445.
Brownlie, L. 1992. Aerodynamic characteristics of sports
apparel. Simon fraser university.
Brownlie, L., Gartshore, M., Mutch, B. & Banister, B.
1987. Influence of apparel on aerodynamic drag in
running. The Annals of Physiological Anthropology, 6,
133-143.
Brownlie, L., Kyle, C. R., Carbo, J., Demarest, N., Haber,
E., Macdonald, R. & Nordstrom, M. 2009.
Streamlining the time trial apparel of cyclists: the nike
swift spin project. Sports technology, 1-2, 53-60.
Cd-adapco 2015. Starccm+ user guide.
Chung, T. J. 2002. Computational fluid dynamics,
Cambridge University Press.
De Groot, G., Sargeant, A. & Geysel, J. 1995. Air friction
and rolling resistance during cycling. Medicine and
science in sports and exercise, 27, 1090–1095.
Debraux, P., Grappe, F., Manolova, A. V. & Bertucci, W.
2012. Aerodynamic drag in cycling: methods of
assessment. Sports biomechanics, 10, 197–218.
Defraeye, T., Blocken, B., Koninckx, E., Hespel, P. &
Carmeliet, J. 2010a. Aerodynamic study of different
cyclist positions: CFD analysis and full-scale wind-
tunnel tests. . Journal of biomechanics, 43, 1262-1268.
Defraeye, T., Blocken, B., Koninckx, E., Hespel, P. &
carmeliet, j. 2010b. Computational fluid dynamics
analysis of cyclist aerodynamics: performance of
different turbulence-modelling and boundary-layer
modelling approaches. Journal of Biomechanics, 43,
2281-2287.
Defraeye, T., Blocken, B., Koninckx, E., Hespel, P. &
Carmeliet, J. 2011. Computational fluid dynamics
analysis of drag and convective heat transfer of
individual body segments for different cyclist
positions. Journal of Biomechanics, 44, 1695–701.
Di Prampero, P. E. 2000. Cycling on earth, in space and
on the moon. European Journal Applied of
Physiology, 82, 345–360.
Hanna, R. K. 2002. Can CFD make a performance
difference in sport? In: Haake SJ, E. (ed.) The
Engineering of Sport 4. Oxford: blackwell science.
Launder, B. E. & sharma, B. I. 1974. Application of the
energy dissipation model of turbulence to the
calculation of flow near a spinning disc. Letters in
Heat and Mass Transfer, 1, 131-138.
Lecrivain, G., Slaouti, A., Payton, C. & Kennedy, I. 2008.
Using reverse engineering and computational fluid
dynamics to investigate a lower arm amputee
swimmer’s performance. Journal of Biomechanics, 13,
2855–2859.
Lukes, R. A., S.B., C. & S.J, H. 2002. The understanding
and development of cycling aerodynamics. Sports
engineering, 8, 59–74.
Menter, F. R. 1994. Two-equation eddy-viscosity
turbulence models for engineering applications. Aiaa
journa, 32, 1598–1605.
Minetti, A. E., Machtsiras, G. & C., M. J. 2009. The
optimum finger spacing in human swimming. Journal
of biomechanics, 42, 2188–90.
Oggiano, L. & Sætran, L. 2012. Experimental analysis on
parameters affecting drag force on speed skaters.
Sports technology, 3, 223-234.
Oggiano, L., Sætran, L., Leirdal, S. & Ettema, G. 2008.
Aerodynamic optimization and energy saving of
cycling postures for international elite level cyclists.
The Engineeeing of Sport 7, 597-604.
Oggiano, L., Troynikov, O., Konopov, I., Subic, A. & F.,
a. 2009. Aerodynamic behaviour of single sport jersey
fabrics with different roughness and cover factors.
Sports Engineering, 12, 1-12.
Spalart, P. R. 2000. Strategies for turbulence modelling
and simulations. Int. J. Heat Fluid Flow 21 (3), 252–
icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support
188
263.
Underwood, L. 2012. Aerodynamics of track cycling.
Doctor of philosophy, the University of Canterbury.
Underwood, L. & Jermy, M. C. Fabric testing for cycling
skinsuits. 5th Asia-pacific congress on sports
technology (APCST), 2011 Melbourne. 350–356.
Wilcox, D. C. 2006. Turbulence modelling for CFD, la
Canada, California, USA.
Zaïdi, H., Fohanno, S., Taïar, R. & Polidori, g. 2010.
Turbulence model choice for the calculation of drag
forces when using the CFD method. Journal of
Biomechanics, 10, 405-11.
Aerodynamical Resistance in Cycling - CFD Simulations and Comparison with Experiments
189
