Using Genetic Algorithm with Combinational Crossover to Solve
Travelling Salesman Problem
Ammar Al-Dallal
Computer Engineering Department, Ahlia University, Manama, Kingdom of Bahrain
Keywords: Genetic Algorithm, Travelling Salesman Problem (TSP), Crossover.
Abstract: This paper proposes a new solution for Traveling Salesman Problem (TSP) using genetic algorithm. A
combinational crossover technique is employed in the search for optimal or near-optimal TSP solutions. It is
based upon chromosomes that utilise the concept of heritable building blocks. Moreover, generation of a
single offspring, rather than two, per pair of parents, allows the system to generate high performance
chromosomes. This solution is compared with the well performing Ordered Crossover (OX). Experimental
results demonstrate that, due to the well structured crossover technique, has enhanced performance.
1 INTRODUCTION
Genetic algorithm is a sort of adaptive worldwide
searching probabilistic optimization algorithm,
which often simulates the procedure associated with
organisms’ inheritance and evolution. It's been
widely applied to the areas of neural network,
combinatorial optimization, economical forecasts
and pattern recognition. The principle concept of the
genetic algorithm is derived from inheritance and
evolution. It is mainly based on mechanism of
biological evolution and genetics principle, in
accordance with natural selection and survival of the
fittest principle, using simple coding technology in
order to resolve complex problems.
Travelling salesman problem (TSP) is one of the
typical NP- completeness problems in combinational
optimization (Yuan et al, 2009). It is described as
follows. A salesman has to visit a number of cities
only once and then returns home. The distances
between any pair of cities are given at first and it is
required to find the shortest path. In which order
should the cities be visited to minimize the distance
travelled?
There are two kinds of TSP, symmetric TSP and
asymmetric TSP. In symmetric TSP, the distance
travelled from city i to city j is equal to the distance
travelled from city j to city i. In asymmetric TSP, the
distance travelled from city i to city j is not equal to
the distance travelled from city j to city i. In this
paper, symmetric TSP is considered.
1.1 The Mathematical Representation
of TSP
In math, the problem may be stated as follows (Yuan
et al, 2009). Given n cities, if V denotes the set of
cities as V = {v
1
, v
2
, v
3
,
…
, v
n
}, and T denotes a
permutation as T = (t
1
, t
2
, t
3
,
…
, t
n
}, where t
i
V,
(i=1,2,3, …,n}, and denoted t
n+1
= t
1
, then TSP is
given as:
(1)
Although this formulation is simple, TSP is hard
to solve. For a symmetric TSP with n cities the
number of possible solution is (n-1)!/2, which is a
very large number even for a relatively small n
(number of cities).
1.2 Genetic Algorithm Representation
of TSP
The search space S is a set consisting of all cities
provided in the dataset. Each path P consists of all
cities of the search space S selected in a random
order. Each chromosome in GA represents a
possible path, and each path is evaluated using a
fitness function f that accumulates the summation of
distances between these cities (more about the
fitness function is explained in Section III). A set of
possible paths (chromosomes) associated with their
Al-Dallal, A..
Using Genetic Algorithm with Combinational Crossover to Solve Travelling Salesman Problem.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 149-156
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
149
fitness value forms one generation. Finally, a GA
engine tries to output a set of paths that minimize the
value of f. The optimal solution is a path or set of
paths that have the minimum score (distance)
returned by the function f.
It is found that such an optimization problem can
be solved efficiently using Genetic Algorithm (GA)
(Yuan et al, 2009; Vahdati et al, 2009, Wang and
Zha, 2009; Zhao et al, 2008; Yu et al, 2011). In
addition, GA demonstrates near global optimality,
implicit parallelism, adaptability, and high
robustness (Yu et al, 2011).
In its simplest form, a GA is a probabilistic
algorithm used to simulate the mechanism of natural
selection of living organisms, and it is often used to
solve problems having expensive solutions in terms
of time and computation complexity. This is due to
the principles of selection and evolution employed to
produce several solutions for a given problem.
Generally speaking, GA’s search space is composed
of candidate solutions to the problem (represent
possible paths in TSP). Each chromosome has an
objective function value known as fitness value that
is the path length joining the cities. This measure is
used to favour selection of successful parents for
producing new offspring. Offspring solutions are
produced from parent solutions by the application of
selection, ocrossover and mutation operators
(Lianshuan, Zengyan, 2009). The Offspring forms
the next generation of possible solution. Following
generations are then created by applying these three
operators until one of the two following criteria is
satisfied. Either the maximum predefined number of
generations is created, or no further enhancement to
chromosomes (in terms of overall fitness value) is
observed, as compared to the previous generation. In
all cases, the system will return the best solution
from the last generation.
The rest of this paper is organized as follows:
Section two lists related work of TSP that is
implemented using GA. Section three describes the
proposed GA model to improve the process of
solving the symmetric TSP. Section four describes
the experiments and results. Finally, Section five
concludes this paper.
2 RELATED WORK
Many approaches and results on evolutionary
optimization for TSP have been published. Samples
of these approaches include the following:
Authors of (Yuan et al, 2009) proposed GA based
on good character breed. The searching space is
divided into segments based on the fine seed. At
first, GA runs several times and gets a perfect
individual every time to gather a fine seed set. To
strengthen the local search, every segment is treated
as a small size TSP to be optimum. This approach
demonstrates a slight improvement when applied to
a small dataset of size 150.
Vahdati et al proposed in (Vahdati et al, 2009) a
new solution for TSP using genetic algorithm. This
technique is based on applying heuristic crossover
and mutation operation to GA in order to prevent
premature convergence.
The heuristic crossover considers each
chromosome as a closed circle. Two pointers are
used for each parent. The decision whether to select
the clockwise or anticlockwise pointer is based on
the fitness. This technique is able to accelerate the
speed of convergence by reducing the number of
generations.
An improved combinational genetic algorithm for
travelling salesman problem is applied in (Wang and
Zhao, 2009). This approach adds a local search
procedure in the standard genetic algorithm. Local
search is performed on the best individual of each
generation. This method increases the stability of the
algorithm in addition to improving the precision.
The authors of (Yu et al, 2011) solved the TSP
using GA in which the algorithm employed a
roulette wheel based selection mechanism, the use of
a survival-of-the-fittest strategy, a heuristic
crossover operator, and an inversion operator. This
approach was applied in TSP with 50 cities, and it
was able to quickly obtain an optimal solution to
TSP from a huge search space. However, this study
is not provided with clear figures to demonstrate the
level of improvement over other techniques as stated
by the authors.
A multi-objective TSP that is implemented using
GA is presented in (Lianshuan and Zengyan, 2009).
It creates an initial population which satisfies the
basic qualification, then it calculates the two
objective-values: distance and cost. The aim is to
find the minimal of both the distance and the cost.
The objective value is then used to rank the
chromosomes with Pareto function. However, this
approach is not provided with clear figures to
demonstrate the level of accuracy and how quickly
the result is obtained.
Takahashi (Takahashi, 2011) suggested solving
TSP through a Combinational method called:
iterative Extended Changing Crossover Operators.
This method combines Edge Assembly Crossover
(EAX) and Ant Colony Optimization (ACO). At the
first stage, ACO tries to search for provisional
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
150

solutions by using initial circuits generated by
uniformly random numbers with a certain random
number called seed. Next EAX follow the
provisional solutions generated by ACO and
continuously searches for the better solutions and
generates individuals having higher fitness. The
provisional solutions compose the chromosomes.
The next solutions are generated by EAX and
merged with new solutions generated by ACO. With
this merged file, EAX is executed again in order to
improve the solutions to create the next optimum
solutions. This approach is applied on medium-sized
TSP dataset and the results shows that it is effective
to produce well performing offspring.
Another approach developed by (Kuroda et al,
2010) is called Z-crossover. The Z-Cross works as
follows: first is to set a zone in the travelling area
according to some rules. Secondly, the edges
connecting cities between inside and outside the
zone are cut. Thirdly, the edges inside the zone of
one parent and those of the other parent are
exchanged. Finally, the sub-tours and isolated cities
produced by the third step mentioned above are
reconnected to construct a new tour of TSP.
Razali and Geraghty in (Razali and Geraghty,
2011) examined the performance of TSP through
analysing three selection techniques. These
techniques are: Tournament Selection, Proportional
Roulette Wheel Selection and Rank-based Roulette
Wheel Selection. The experiments are performed on
datasets with sizes between 10 and 51 cities. The
results show that the tournament selection
outperforms the others where it achieved the best
solution quality with low computing times.
The authors of (Sallabi and El-Haddad, 2009)
proposed an improved genetic algorithm to solve the
TSP. They suggested two crossover techniques. The
first one is the swapped inverted crossover. It can be
applied to a one or two-point crossover. After
partitioning the chromosomes, the genes within the
each partition are flipped in their order and then
swapped between parents. The second suggested
crossover is the rearrangement crossover. It works
by finding the greatest or maximum value of a city
distance among all the adjacent cities on the tour,
and then swap city i with three other cities, one at a
time. This method may not achieve improvement
after several iterations but may take a big jump and
improve the result.
A comparative study is done by Otman and
Abouchabaka (Otman and Abouchabaka, 2012) to
investigate the performance of six crossover
techniques that are applied to solve TSP. These
crossover techniques include: Uniform Crossover
Operator, the Cycle Crossover, the Partially Mapped
Crossover, the Uniform Partially-Mapped
Crossover, the Non-Wrapping Ordered Crossover
and the Ordered Crossover (OX). The experiments
were done on one instance of TSPLIB that is
BERLIN52. The results confirm that the best known
solution for the TSP instance was obtained by using
the OX.
(Osaba et al, 2013) applied multi-crossover and
adaptive island based population algorithm to solve
routing problems such as TSP. In this technique, the
entire population is divided into subpopulations,
each with a different crossover function, which can
be switched according to the efficiency. Each
subpopulation begins with a very low value of
crossover probability and then varies with the
change of the current generation number and the
search performance of recent generations.
As mentioned above, several approaches are
applied to solve TSP. The main contribution of this
work is to develop two new crossover techniques:
Two-Point Crossover with Replacement and
Combinational Crossover as well as adopting
specific GA operators in order to investigate their
performance compared to well-performing
techniques.
3 THE PROPOSED GA FOR
SOLVING TSP
This section describes the proposed GA model by
explaining its components and operators.
3.1 Chromosome Representation
As a matter of fact, chromosomes in GA are used to
represent the possible solution for the problem under
consideration. The chromosome consists of genes
that when integrated together form the complete
solution. For TSP, the best representation is to use
integers to refer to cities numbers. Each
chromosome consists of a sequence of integers to
represent a possible path that the salesperson may
visit. The order of these cities within the
chromosome represents the order of cities to be
visited. A problem with 7 cities is represented as a
chromosome of 7 genes as shown in Figure 1. This
chromosome forms a possible solution that is a path
starts from city number 2 passes through cities 5 - 1 – 4
– 6 - 7 -3 and ends at 2 again, since the path must be
closed path.
Using Genetic Algorithm with Combinational Crossover to Solve Travelling Salesman Problem
151

Figure 1: Sample chromosome.
3.2 Initial Generation Creation
When looking at the methods of creating initial
generation, there is a trade-off between creating an
initial generation in a fast way with low quality or
slower way but with higher quality. Fast creation is
done by selecting individuals randomly without any
selection criteria. However, this method may stick at
a local optimum solution causing the results to be
less effective due to fast convergence (Aly, 1990).
Since there is no specific criterion that favours any
city, a pure random selection is applied to select the
genes (cities) of the initial generation.
3.3 Parent Selection
Once the first generation is created, the operators of
GA are applied. The first operator of GA is parent
selection. Based on the results obtained by (Razali
and Geraghty, 2011), the tournament selection is
adopted in this work.
In tournament selection (Yeh, 2007), a group of i
individuals are randomly chosen from the
population. This group takes part in a tournament
and an individual with highest fitness value wins. In
many cases i is chosen to be two, and this method is
called binary tournament selection. To further
enhance this selection, i is selected to be five. And
the best of these five is selected.
In order to speed up convergence and avoid
creating large number of generation, elitism
technique can be applied as a selection technique
(Asllani and Lari, 2007). In this technique best l
members from the current generation are selected to
form the mating pole for next generation. It is
applied to ensure gradual improvement of the
solution. In this paper, l is selected to have best two
thirds of the current generation, i.e. the best 67% of
the current population.
A validation process, before applying crossover,
is applied to insure that the two selected parents are
different from each other, i.e. P1
P2.
3.4 Fitness Function
The fitness function f is used to evaluate each
individual (chromosome) to determine the best 67%
chromosomes of the population.
It is evaluated by accumulating the sum of
distances between the adjacent cities forming a path.
Assume that a chromosome has a length of n cities,
then the fitness function is calculated as follows
(Vahdati et al., 2009):
(2)
And
is the distance between city c
i
and c
i+1
. If both cities have x and y coordinates, then
the distance is calculated as:
(3)
3.5 Crossover Operator
One of the main operators that heavily affects the
performance of GA system is crossover. In
literature, many techniques of crossover have been
developed and analysed to study their effect on the
output from several perspectives. In all cases,
crossover is performed such that the order of the
genes, hence the developed path, is changed in a
systematic manner to produce a new visible solution.
While many approaches are developed by
researchers to enhance the performance of GA, this
work is featured by introducing two new crossover
techniques that are expected to improve the
performance of the proposed system. The first
proposed crossover technique is called Two Point
Crossover with Replacement (TPXwR). The second
proposed crossover technique is called
Combinational Crossover Technique (CXT). These
two crossover techniques will be investigated in
terms of improvement of finding the shortest path.
3.5.1 The Design of Two Point Crossover
with Replacement (TPXwR)
The technique proposed in TPXwR is derived from
the two-point crossover, and it works like this:
Two chromosomes (parents) are selected from
best 67% (two-thirds) of the current generation using
binary tournament selection. These parents are
named p1 and p2. Then, two crossover points cp1
and cp2 are selected randomly. These two points
will divide each parent into three portions. Let a, b
and c be the portions of p1 and d, e and f be the
portions of p2 as shown in Figure 2.
Two offsprings O
1
and O
2
are formed from these
parents. Offspring one is created according to the
following steps. The first and last portions a and c
are copied to the corresponding positions of O
1
.
Then portion e of p2 is copied to O
1
. If a gene of
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
152
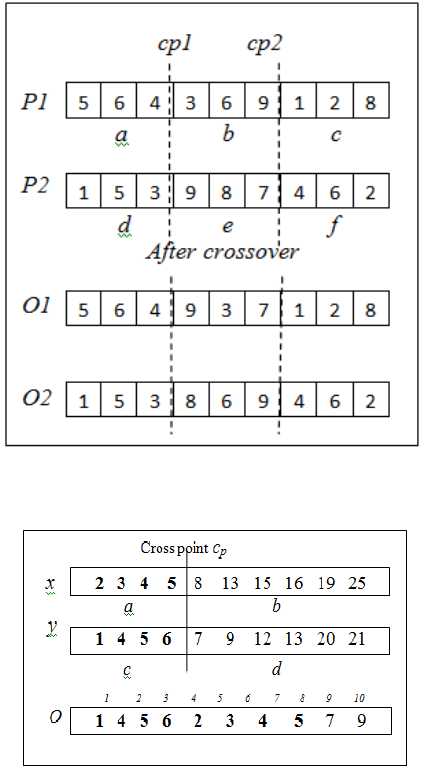
portion e is already existed in O
1
, then it will be
replaced by a gene from portion d of p2. If genes of
d are again exist in O
1
, then it will be replaced by a
gene from portion f.
To create the second offspring O
2
, similar steps
are applied. The first and last portions d and f are
copied to the corresponding positions of O
2
. Then
portion b of p1 is copied to O
2
. If a gene of portion b
is already existed in O
2
, then it will be replaced by a
gene from portion a. If genes of a are again exist in
O
2
, then it will be replaced by a gene from portion c.
During this process, the uniqueness of genes
(cities) within the newly created chromosome is
preserved. Figure 2 provides an example of this
technique where the steps to create the offspring are
as follow:
1. Genes of portions a and c are copied directly
to the corresponding position of the first
offspring O
1
since these are the first genes
added and no need to check their uniqueness.
2. Genes of portion e are copied to the
corresponding position of the first offspring
after checking the uniqueness of genes. 9 and
7 are added from e.
3. If the added gene to the offspring is already
existed in O
1
(8 from e in this example) then
it is replaced by one from portion d, having
that it does not already exist in this offspring
(3 from portion d). Otherwise, it is replaced
with one from portion f.
4. Similar steps are applied when creating the
second offspring with reversing rules.
This technique is considered to be an example of
simple two-point crossover technique but with
replacement when the newly added gene is already
existed in the constructed chromosome. Apparently,
it could produce better offspring compared to their
parents. However, a good generated chromosome
(path) could be disrupted or broken if the crosspoints
happen to be somewhere within a good block
causing it to break an optimal path.
3.5.2 The Design of Combinational
Crossover Technique (CXT)
The second proposed crossover technique is the
Combinational Crossover Technique (CXT). This
technique is applied to a semi-ordered chromosome.
In the semi-ordered chromosome, the first two genes
(cities) are ordered such that these genes have the
shortest path among the paths between all genes of
this chromosome. The closest cities (shortest paths)
appear to the left of the chromosome. The process of
reordering of genes is done after creating the
chromosome.
The proposed CXT also applies the fusion
crossover (Vrajitoru, 1998), where only one offspring
is generated from two selected parents. In this
technique, the offspring inherits the genes from one
of the parents with a probability according to its
performance. The advantage of this technique is that
the good genes of both parents are inherited
simultaneously to the offspring, producing high-
quality offspring and increasing the speed of
convergence.
Figure 2: Example to illustrate the TPXwR crossover
technique.
Figure 3: Example to illustrate the CXT crossover
technique.
The CXT technique is explained through the
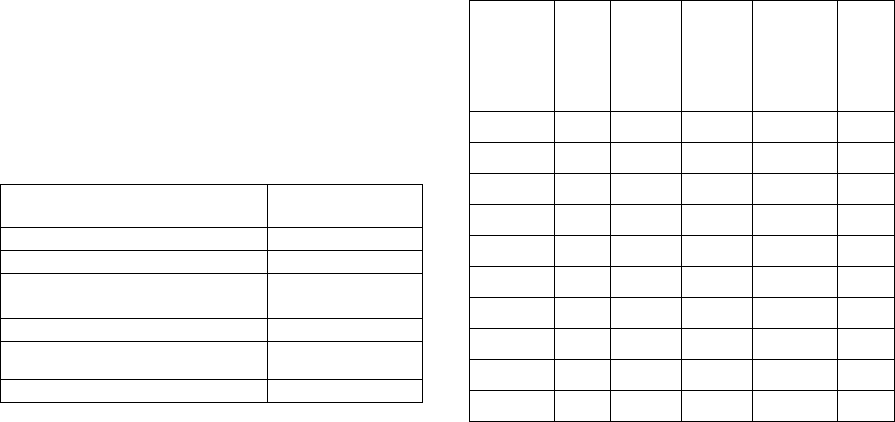
example depicted in Figure 3. The number of cities
in this example is 10 and the numbers inside the
chromosomes represent the length between nodes i
and i+1, and i is between 1 and 10 according to the
mathematical model explained in Section I.
Using Genetic Algorithm with Combinational Crossover to Solve Travelling Salesman Problem
153
1. Select two parents x and y randomly from the
best 67% chromosomes of the current
generation.
2. Select one crosspoint randomly. This
crosspoint will divide x into two portions a and
b. Also, y will be divided into two portions c
and d.
3. Calculate the fitness of the first gene of each
parent. That is the first gene of portions a and c.
4. The one that has the lower fitness values is
selected as parent 1. In this example, y is
selected as parent 1 since the fitness of the first
gene is 1 which is less than 2 for parent x.
5. Copy the genes from the left portion (portion c
in this example) to the left portion of the
offspring O.
6. Continue filling the offspring with the genes
from the left portion of the second parent to the
offspring (portion a). Need to maintain the
length of the offspring equal to the parent’s
length. That is the genes from the second
parent will be copied until the length of the
offspring is equal to the parent’s length.
7. If the length of the offspring is still smaller
than the parent’s after the previous step, then
more genes need to be copied from either
parent.
8. The fitness values of genes of portions b and d
are compared starting from location cp+1. The
portion with the gene that has a lower fitness
value will contribute to the offspring O. This is
done in order to generate offspring with
appropriate genes from each parent and to
guarantee that the length of O is equal to the
length of the parent.
9. Through the process of copying the remaining
genes from the parents, the uniqueness of the
copied genes must be considered, i.e., each
gene can occur only once in the new offspring.
10. Last step is to order the genes based on their
fitness value. The order is done in ascending
order as preparation for the next crossover
process.
The rationale behind selecting the portion with the
lower fitness to start with is the need to inherit the
good order of cities and maintain the good building
blocks while passing them to the resulting offspring.
4 EXPERIMENTS AND RESULTS
This section describes the data set used to test the
performance of the proposed technique. Then it
analyses the obtained results.
4.1 Dataset Description
In order to investigate the performance of the
proposed techniques, several experiments need to be
conducted on a benchmark dataset. 10 instances are
chosen from TSPLIB (Reinelt, 1991) to perform the
needed experiments. These 10 sets differ in size and
ranging from 22 cities to 318 cities.
The proposed GA system starts by creating initial
generation consisting of 50 chromosomes. Recall
that each chromosome forms a possible solution
(travelling path). Hence, the length of the
chromosome is equal to the number of cities of the
applied dataset. The stopping condition of the
proposed system is one of the following: either the
maximum predefined number of generations is
created, or no further enhancement to chromosomes
(in terms of overall fitness value) is observed, as
compared to the previous generation. The crossover
probability is chosen to be 1. These parameters are
listed in Table 1.
4.2 Analysis of the Results
In order to evaluate the proposed crossover
techniques, they are compared with the results
obtained by applying the algorithm explained in
(Otman and Abouchabaka, 2012). As mentioned in
Section II, OX has obtained best results among six
options of crossover techniques.
The considered results of the experiments are the
chromosomes of the last generation. These results
are illustrated in Table 2. The first column is the
name of the dataset. The number associated to the
dataset name reflects the size of the set. The next
three columns are the results obtained from TPXwR,
CXT and OX techniques. The last two columns
provide the improvement in the fitness value of CXT
compared to OX and TPXwR.
When comparing the two proposed crossovers,
the CXT which produces one offspring in each
crossover process, shows better performance in
general in terms of the shortest path (fitness value).
For all sets, CXT achieves shorter path than TPXwR
except for berlin52 dataset. The improvement of
CXT over TPXwR ranges between 1.3% and
17.19%. The reason behind this improvement is that
in CXT the offspring inherits the well-performing
building blocks from parents that include adjacent
cities with minimal distance. Repeating this process
in every generation provides a great chance to
achieve better results, having that both techniques
are producing the same number of generations.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
154
By analysing the results obtained by the two
proposed techniques and the results obtained by the
well know OX technique, it can be noticed that CXT
outperforms OX by percentage starting from 2.86%
for only one dataset, i.e. lin318 dataset and increases
to reach maximum of 22.38% for the eil76.
When looking at the results of the last
generations, it ascertains that the proposed crossover
is successful in enhancing the chromosome
performance since the aim of this process is to
produce better offspring from the parents.
The main reason behind the improvement in
performance is the way of implementing CXT. The
main contribution to the high improvement is
coming from the method of adding first genes to the
offspring. The first added genes are added based on
the fitness value (path length). The cities with lower
path length form a “good” building block. One of
the objectives when developing a crossover
technique is not to destruct these well performing
building blocks. And this is what is achieved in this
technique. This “good” building block is inherited
unchanged to the offspring. Not only this but also
the best building block of the second parent is also
passed to the offspring. Hence, each crossover
process adds two “good” building blocks to the
created offspring causing an enhancement in the
fitness value.
Table 1: Parameter setting of GABIR.
Parameter Description
Value
Population size
50
Maximum number of generations
200
Chromosome length
No. of cities of the
running set
Crossover rate
1
The number of best individuals
forming the crossover mate (Elitism)
2/3 of the population
Mutation rate
0.1
5 CONCLUSIONS
One of the permanent challenges for TSP problem is
to find the optimal solution (shortest path) using a
simple solution.
This paper applied a GA-based system to solve it
by developing two crossover techniques. The first
one is the 2-point crossover with replacement
TPXwR that produces two offspringss in each
crossover operation. However, this technique is
defective, where using multiple crosspoints causes
many breaks in good behavioural building blocks.
This in turn delays the convergence process. In order
to overcome this drawback, another crossover
technique is proposed. This crossover is the
Combinational Crossover Technique CXT. It works
by applying one-point crossover on an ordered
chromosome to produce only one offspring. The
experiment was applied on 10 datasets ranging in
size from 22 and 318 cities and compared to well-
performing OX crossover technique.
The results obtained show that the CXT
outperforms both TPXwR and OX. The
improvement of CXT ranges between 1.3% to
around 17% compared to TPXwR and ranges
between 2% and 22.4% compared to OX.
To generalize the results and further demonstrate
its efficiency, the proposed techniques need to be
compared with additional crossover techniques such
as the Uniform crossover, Edge Assembly Crossover
and Ant Colony Optimization. In addition, they need
to be applied on bigger TSP datasets.
Table 2: The fitness of each date set after last generation.
Dataset
CXT
TPXwR
OX
% Impr. of
CXT over
TPXwR
%
Impr.
of CXT
over
OX
ulysses22
1310
1480
1582
11.49%
17.19
att48
1211
1461
15356
17.14%
21.12
eil51
1370
1407
1530
2.63%
10.43
berlin52
2625
2506
2951
-4.75%
11.05
st70
3129
3182
3730
1.67%
16.10
eil76
1971
2285
2539
13.74%
22.38
rat99
7617
8054
8333
5.43%
8.59
kroA100
1483
1522
1686
2.53%
11.97
gr120
9389
10182
10886
7.79%
13.76
lin318
5686
5762
5854
1.31%
2.86
REFERENCES
Yuan L., Lu Y., Li M., 2009. "Genetic Algorithm Based
on Good Character Breed for Traveling Salesman
Problem," 1st International Conference Information
Science and Engineering (ICISE), pp.234,237, 26-28
Dec.
Vahdati, G., Yaghoubi, M., Poostchi, M., Naghibi S,
M.B., 2009. "A New Approach to Solve Traveling
Salesman Problem Using Genetic Algorithm Based on
Heuristic Crossover and Mutation
Operator," International Conference of Soft
Using Genetic Algorithm with Combinational Crossover to Solve Travelling Salesman Problem
155

Computing and Pattern Recognition. SOCPAR '09,
pp.112,116, 4-7 Dec.
Wang S., Zhao A., 2009. "An Improved Hybrid
Genetic Algorithm for Traveling Salesman
Problem", International Conference on Computational
Intelligence and Software Engineering,. CiSE 2009. ,
vol., no., pp.1,3, 11-13 Dec.
Zhao G., Luo W., Nie H., Li C., 2008. "A Genetic
Algorithm Balancing Exploration and Exploitation for
the Travelling Salesman Problem," Fourth
International Conference on Natural Computation,
ICNC '08. , vol.1, pp.505,509, 18-20 Oct.
Yu Y., Chen Y., Li T., 2011. "A New Design of
Genetic Algorithm for Solving TSP," Fourth
International Joint Conference on Computational
Sciences and Optimization (CSO), pp.309- 313, 15-19
April.
Lianshuan S., Zengyan L., 2009. "An Improved Pareto
Genetic Algorithm for Multi-objective TSP," Fifth
International Conference on Natural Computation,
ICNC '09 , vol.4, pp.585,588, 14-16 Aug.
Takahashi, R., 2011. "Solving the Traveling Salesman
Problem through Iterative Extended Changing
Crossover Operators," 10th International Conference
on Machine Learning and Applications and
Workshops (ICMLA), 2011, vol.1, pp.253,258, 18-21
Dec.
Kuroda, M., Yamamori, K., Munetomo, M., Yasunaga,
M., Yoshihara, I., 2010. "A proposal for Zoning
Crossover of Hybrid Genetic Algorithms for large-
scale traveling salesman problems," IEEE Congress
on Evolutionary Computation (CEC), , vol., no.,
pp.1,6, 18-23 July.
Razali M.. R., and Geraghty J., 2011. "Genetic algorithm
performance with different selection strategies in
solving TSP”, World Congress Engineering 2011, vol
II WCE,(London UK).
Sallabi O., El-Haddad Y.. 2009. An Improved Genetic
Algorithm to Solve the Travelling Salesman Problem.
World Academy of Science, Engineering and
Technology. vol.52, pp. 471-474.
Otman A., Abouchabaka J., 2012. "A comparative study
of adaptive crossover operators for genetic algorithms
to resolve the traveling salesman problem." IJCA,
vol.31, no. 11, pp. 49-57.
Osaba E., Onieva E., Carballedo R., Diaz F., Perallos A.,
and Zhang X., 2013. “A multi-crossover and adaptive
island based population algorithm for solving routing
problems,” Journal of Zhejiang University SCIENCE
C, vol. 14, no. 11, pp. 815–821.
Aly A., 1990. “Applying genetic algorithm in query
improvement problem”. Information Technologies and
Knowledge, vol.1, pp. 309-316.
Yeh, J.-Y., Lin, J.-Y., Ke, H.-R., and Yang, W.-P., 2007.
“Learning to rank for information retrieval using
genetic programming”. In Proceedings of ACM SIGIR
Workshop on Learning to Rank for Information
Retrieval (LR4IR '07), pp. 41-48. Amsterdam,
Netherlands.
Asllani, A., Lari, A., 2007. “Using genetic algorithm for
dynamic and multiple criteria web-site optimization”s,
European Journal of Operational Research, Volume
176, Issue 3, 1 February 2007, pp. 1767-1777.
Vrajitoru D., 1998. “Crossover improvement for the
genetic algorithm in information retrieval”.
Information Processing and Management , vol. 34, no.
4, ,pp. 405-415.
Reinelt G., 1991. “TSPLIB – a traveling salesman
problem library”, ORSA Journal on Computing, ,
Vol.3, No.4, pp.376-384.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
156
