Genetic Algorithm as Machine Learning for Profiles Recognition
Yann Carbonne
1
and Christelle Jacob
2
1
University of Technology of Troyes, 12 rue Marie Curie, Troyes, France
2
Altran Technologies, 4 avenue Didier Daurat, Blagnac, France
Keywords: Genetic Algorithm, Machine Learning, Natural Language Processing, Profiles Recognition, Clustering.
Abstract: Persons are often asked to provide information about themselves. These data are very heterogeneous and
result in as many “profiles” as contexts. Sorting a large amount of profiles from different contexts and
assigning them back to a specific individual is quite a difficult problem. Semantic processing and machine
learning are key tools to achieve this goal. This paper describes a framework to address this issue by means
of concepts and algorithms selected from different Artificial Intelligence fields. Indeed, a Vector Space Model
is customized to first transpose semantic information into a mathematical model. Then, this model goes
through a Genetic Algorithm (GA) which is used as a supervised learning algorithm for training a computer
to determine how much two profiles are similar. Amongst the GAs, this study introduces a new reproduction
method (Best Together), and compare it to some usual ones (Wheel, Binary Tournament).This paper also
evaluates the accuracy of the GAs predictions for profiles clustering with the computation of a similarity
score, as well as its ability to classify two profiles are similar or non-similar. We believe that the overall
methodology can be used for any kind of sources using profiles and, more generally, for similar data
recognition.
1 INTRODUCTION
For several years, we have witnessed the exponential
growth of data worldwide. According to the experts,
90% of world data had been generated over the last
two years. Human cannot handle this large amount of
data, hence machine comes in the foreground for
processing and extracting meaningful information
from them.
In this paper, we will focus on a special kind of
data: those concerning people. These data can be very
heterogeneous due to the diversity of their origin.
Data comes from several sources: public (social
media, forums, etc.) or private (employee database,
customer database, etc.).
Despite their diversity, collected data are
processed the same way: each user (a real person) is
matched with one or several profiles. A profile could
contain global information (city, gender …) or
specific information (work history …). The
information volume could also be dense or sparse.
This paper differs from existing studies about
profiles recognition in social networks (Rawashdeh &
Ralescu, 2014) because it does not focus on similarity
between profiles within a social network but between
different social networks. Even if existing solutions,
such as the use of Vector Space Models (VSM) for
information retrieval (Salton, 1968), inspired our
study, they are not straight related.
The problem is to identify the same real person
between different profiles from different sources.
To do so, the objective is to teach a computer to
automatically answer the question: “Are these two
profiles about the same real person?”. Just like it
would be for a human, the teaching will be split in
two phases. During a first phase, the computer will
use a human-made set of data to train. Within this
training set, for each possible combination of profiles,
the question above had been answered. The training
should be done with various profiles from different
sources to be relevant. After the training phase, the
computer will be able to predict a similarity score
between two profiles. The performances will be
determined through the analysis of predefined criteria
for predictions.
In this study, we investigate how to determine a
person profile using a combination of natural
language processing, genetic algorithm and machine
learning. In addition, we propose a new reproduction
mechanism, named here Best Together (BT). The
Carbonne, Y. and Jacob, C..
Genetic Algorithm as Machine Learning for Profiles Recognition.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 157-166
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
157

new reproduction is compared with other methods
such as Wheel and Binary Tournament. Results
indicate BT as a promising strategy for profile
recognition.
This paper is organized as follows: Section 2
introduces how to convert a profile (a set of semantic
information) to a mathematic model, understandable
for a computer. Section 3 describes the overview of
the genetic algorithm used to train the computer for
profile recognition. Section 4 analyses the results of
the prediction made by our model and it will be
followed by our conclusions.
2 MATHEMATICS DESIGN FOR
PROFILES
2.1 Representation of a Profile
First of all, let us introduce the mathematical model
used for profiles representation. A profile will be
considered as a set of labelled semantic information.
For example:
Table 1: Profile example.
Information Label
Foo firstname
Bar lastname
Paris city
beer like
In order to be able to compare several profiles on
a same frame of references, we will use the Vector
Space Models (VSM) of semantics.
Indeed, computers have difficulty understanding
semantic information but VSM provides a solution
for this problem. They have widely been used in
different fields as a recent survey highlights (Turney
and Pantel, 2010). In particular, they have been
successfully used in the field of Machine Learning for
classification (Dasarathy, 1991) and also for
clustering (A. K. Jain, 1999).
Within a VSM, each profile P
x
will be transposed
as a vector V
x
with N
x
dimensions which are all the
information in the profile P
x
. For example, the profile
above will be a vector with the dimensions: “Foo”,
“Bar”, “Paris” and “beer”.
The value of V
x
in a specific dimension δ will be
a weighting from the label matched with the
information δ.
The VSM consists in creating a new vector space
of M dimensions. For two vectors V
x
and V
y
, the
dimension M is set as:
M = N
x
∪ N
y
(1)
Whenever transposing a vector into a VSM, the
vector has a value 0 on its non-existing dimensions.
Illustration to the use of VSM with an example :
considering two profiles P
1
and P
2
:
Table 2: Contents for profiles P
1
and P
2
.
P
1
P
2
Foo firstname Foo firstname
Bar lastname Bar lastname
Google organisation Horses like
Paris city Google like
For the purpose of this example, the weighting for
each label are:
Table 3: Weighting example.
Label Weight
firstname 0.7
lastname 0.8
organisation 0.4
city 0.5
like 0.1
The associated VSM, with the vector V
1
for P
1
and
V
2
for P
2
, will be:
Table 4: VSM for V
1
and V
2
.
Dimension V
1
V
2
Foo 0.7 0.7
Bar 0.8 0.8
Google 0.4 0.1
Paris 0.5 0
Horses 0 0.1
The advantage of this representation is to keep the
semantic information in the forefront of the
mathematic analysis. In the example above, both
profiles have the information “Google” but for one,
this information is labelled as “organisation” and for
the other, it is labelled as “like”. Even with these
different labels, this model will consider the
information important but at a different scale. By
intuition, we would like to set the label “organisation”
at a higher value than the label “like” because the
former is usually more relevant to distinct two
profiles than the later. We acquired this intuition
through our experience and we would like the
computer to get the same “intuition” for any kind of
labels.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
158
2.2 Similarity Function
Once the VSM for two vectors V
x
and V
y
is created,
the usual method is to compute their similarity with
the cosine (Turney and Pantel, 2010):
similarity (V
x
,V
y
) = cos (α) (2)
where α is the angle between V
x
and V
y
.
This similarity rate gives a good clue of how close
two vectors are within their vector space, therefore
how similar two profiles are.
But there is a human intuition in profiles
recognition that is missing with this computation.
Sometimes, two profiles do not contain enough
relevant information to evaluate their similarity. For
example, if two profiles like the same singer and these
profiles only contain this information, it is not enough
to determine they both concern the same person.
Through experimentation, we noticed that the norm
of a vector is a good metric to evaluate the relevance
of a profile. Therefore, the similarity rate is smoothed
with the average norm of the two vectors:
similarity(V
x
,V
y
) = cos(α) * (‖V
x
‖ + ‖V
y
‖) / 2
(3)
where ‖V‖ is the Euclidean norm for the vector V. The
factor (‖V
x
‖ + ‖V
y
‖) / 2 goes through a repair function
which assures it stays in the real interval [0,1].
This similarity rate is a real value in [0,1] and it
can be interpreted as a percentage. For example, a rate
of 0.27 corresponds to 27% of similarity.
To sum it up, making use a VSM is an effective
process to move from semantic information to a
mathematic model which will be used to compute
effectively the similarity between two profiles. The
next step is to teach the computer to find dynamically
the weighting for each label. For this purpose, a
genetic algorithm is applied in this study.
3 GENETIC ALGORITHM
Genetic algorithms (GA) are heuristics, based on
Charles Darwin’s theory of natural evolution, used to
solve optimization problems (Hüe, 1997). The
general process for a GA is described as follows
(Eberhart et al., 1996), (Kim and Cho, 2000):
Step 1: Initialize a population.
Step 2: Compute the fitness function for each
chromosome in the population.
Step 3: Reproduce chromosomes, based on their
fitness.
Step 4 : Perfom crossover and mutation.
Step 5 : Go back to step 2 or stop according to a
given stopping criteria.
GA can also be used as Machine Learning (ML)
algorithm and has been shown to be efficient in this
purpose (Goldberg, 1989). The idea behind is that
natural-like algorithms can demonstrate, in some
cases in the ML field, a higher efficiency compared
to human-designed algorithms (Kluwer Academic
Publishers, 2001). Indeed, actual evolutionary
processes have succeeded to solve highly complex
problems, as proved through probabilistic arguments
(Moorhead and Kaplan, 1967).
In our case, GA will be used to determine an
adequate set of weighting for each label present in a
training set. Our training set is composed with
similarities between profiles, two profiles are either
similar (output = 1) or not similar (output = 0).
3.1 Genetic Representation
The genotype for each chromosome of the population
will be the group of all labels in the training set. Each
label is defined as a gene and the weighting for a
specific label is the allele of the linked gene. The
weighting is a value in [0,1], it could be translated as
the relevance of a label and it reaches its best at value
1 and worst at 0.
3.2 Population Initialization
For population initialization, there are two questions
: “What is the initial population size ?” and “What is
the procedure to initialize the population ?”.
About the population size, the goal is to find a
compromise between the global complexity and the
performance of the solution (Holland, 1992). A small
population may fail to converge and a large one may
demand an excessive amount of memory and
computation time. It turns out that the size of the
initial population has to be carefully chosen, tailored
to address our specific problem.
As a reminder, in our problem, the GA have to
compute weighting for a number N of labels in the
training set. We evaluated different values for the
population size, compromised between efficienty and
complexity and chose to fix the population size to
2×N.
Secondly, to initialize a population, there are
usually two ways: heuristic initialization or random
initialization. The heuristic initialization, even if it
allows to converge faster to a solution, has the issue
to restrain the GA to search solutions in a specific area
and it may fail to converge to a global optimum (Hüe,
1997). A random initialization is a facilitating factor
for preventing GA to get stuck in a local optima.
In our case, the random initialization consists in
Genetic Algorithm as Machine Learning for Profiles Recognition
159

giving a random weighting between [0,1] for each
gene within the genotype.
3.3 Fitness Function
The main purpose of a fitness function is to evaluate
a chromosome, based on how well it fits the desired
solution (Hüe, 1997).
In our case, chromosomes are evaluated on how
well they fit the training set, using the VSM method
to predict similarities. We chose to use a fitness
function which is widely used in the ML field (Shen,
2005), as our problem can be related to a regression
problem. It is called the logarithmic loss which is
defined as follows:
loss= -
1
M
(y
i
log
M
i=1
p
i
+
1- y
i
log(1- p
i
))
(4)
where M is the number of examples in our training
set, y
i
is the output (0 or 1) of the ith example and p
i
is the output in [0;1] from the current chromosome.
To prevent the asymptote at 0 from the logarithmic
function, the predicted output p is replaced with:
p:maxmin
p,1‐10
‐15
,10
‐15
(5)
3.4 Crossover
Crossover is the artificial reproduction method for a
GA. It has to define how two selected chromosomes
will produce an offspring. Crossover is crucial for
GA, causing a structured exchange of genetic
information between solutions which could lead good
solutions to better ones (Srinivas and Patnaik, 1994).
We chose to use the arithmetic crossover with an
alpha parameter at 0.5. This crossover creates
children that are the weighted arithmetic mean of two
parents:
offspring = 0.5 * parent1 + 0.5 * parent2 (6)
3.5 Mutation
Mutation forces some chromosomes to change and it
allows the GA to get away from a local optima (Hüe,
1997).
In our case, the risk to get stuck in a local optima
is present. Indeed, the aim for our GA is to find the
optimized weighting for a set of labels which consists
in finding the relevant labels (high weighting) and the
non-relevant ones (low weighting), consequently
creating an ordering for the labels. Local optima
would consists of a version of the GA detecting that,
for example, the label “lastname” is relevant to find
some similarities within the training set. This result
will lead to a better fitness function. But it would be
a local optima due to the necessity to find the right
weighting and ranking for each label. The GA should
be defined with a sufficient amount of diversity which
will allows keeping a good weighting for a specific
label but still enabling variation to the other labels.
Therefore, we chose to implement a mutation
method which enhances the diversity.
Beside the mutation chance M
c
, which determines
the chance for an offspring to mutate, we set up a
mutation rate M
r
. If a new chromosome mutates (i.e.
if a random number in [0,1] < M
c
), each of its alleles
will vary depending on a random factor F in [1 - M
r
,
1 + M
r
]. Of course, a repair function is applied to
ensure that each allele stays in [0,1].
3.6 Reproduction
The reproduction (or selection) method is intended to
improve the average quality for a new generation. To
fulfill this goal, this method usually follows the
Darwin’s principle that the fittest chromosomes will
tend to reproduce more (Hüe, 1997).
There are two categories of reproduction methods:
proportionate and ordinal-based.
The first one is based on the fitness value and
gives each chromosome a chance to reproduce
proportionally to its value. A typical method is the
wheel (Goldberg, 1989). We consider a wheel where
each chromosome has a portion with a size
proportional to its score. To select partners for
crossover, we simply “launch” the wheel. With this
method, each chromosome has a chance to be a
parent, even so, statistically, the fittest chromosomes
might have a better chance than the others.
On the contrary, for ordinal-based methods, the
chromosomes are ranked according to their fitness
and the selection is based upon the rank of a
chromosome within the population. A classical
approach is the use of the tournament method (Miller
and Goldberg, 1995). This method needs to get a
parameter S (tournament size) which determines the
size for a round. In fact, this method proceeds round
after round. At each round, S chromosomes are
randomly selected, the highest-ranked chromosome
wins the round and it is selected for crossover.
However, for this specific problem of profiles
recognition, we came up with a new idea which will
be presented afterwards. Then, we will show the
results in comparison with the state of the art of
reproduction method.
Usually, a GA have a low mutation chance (~
0.05) which leads to a controlled diversity. The
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
160

reproduction method also controls the diversity by
letting globally a chance for each chromosome to be
selected for crossover.
The idea of our GA is to set up a huge mutation
factor (Section 3.5) which will ensure the diversity of
our algorithm and prevent it to get stuck in a local
optima. Beside this point, the tactic is to have a highly
selective reproduction method which allows to get rid
of all non-adequate chromosomes. To sum up, a
generation will have a lot of diversity but will quickly
throw non-suitable chromosomes away. The diversity
is assured by our mutation method, so we just need
the reproduction method to be selective.
Consequently, we created our own reproduction
method, labelled as Best Together (BT). It is inspired
by the idea of considering only an elite group of
chromosomes for reproduction, introduced with the
incoming of Biased Random-Key Genetic
Algorithms (Resende, 2010). It is an ordinal-based
method; thereby it is necessary to rank the population.
For a population of size N, this method will select a
number X of the best chromosomes. Each of these
selected chromosomes will reproduce with all others
selected chromosomes. We know that it leads to a
number of crossover equals to:
X * (X – 1) / 2
(7)
Each crossover producing an offspring, the
population size needs to stay approximately the same.
To do so, we need the equation 7 to be equal to N,
which leads to the following polynomial equation:
X² - X – 2*N = 0 (8)
The X computed by the BT method is the positive
solution of this quadratic form (which always exists
because if a = 1 and c = -2, then the determinant ≥ 0).
The solution might be a real number, therefore only
the floor of X is kept. It slightly decreases the
population size but it does not really affect the quality
of the GA.
As we explained, once the BT method has
computed this value X, it takes a group of X best
chromosomes and applies crossover with all
combinations, except for a chromosome with itself.
3.7 Comparison
In (Section 3.6), we presented a new reproduction
method which differs from the state of the art. In this
section, we will compare it with some state of the art
GA over our training set.
We compared 3 GA with the following
parameters:
1) A wheel reproduction.
2) A tournament reproduction with a
tournament size 2 (binary tournament).
3) Our BT reproduction method.
For the figure 1, we set M
c
= 0.75 and M
r
= 0.8, which
is considered as a large mutation chance and we saved
the best score for the fitness function in each
generation.
Figure 1: Comparison of reproduction with a large
mutation.
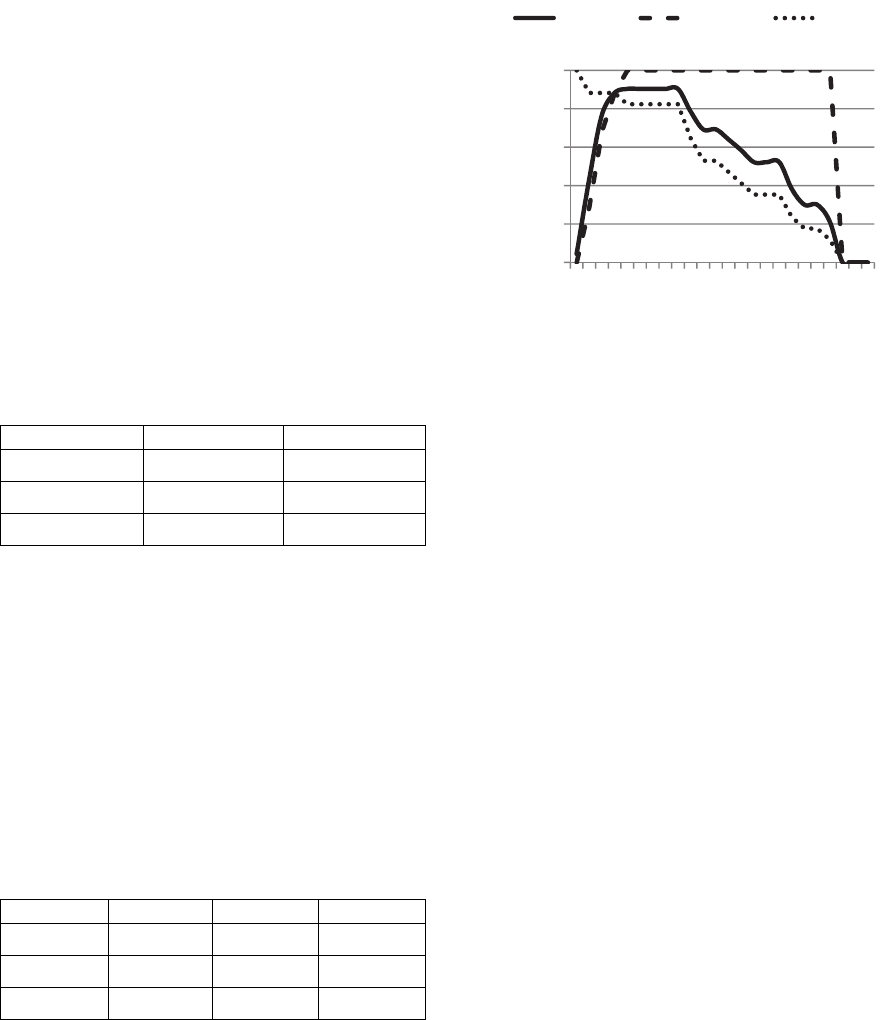
The BT method converges faster than the Wheel and
Tournament methods: it reaches a LogLoss value
below 0.17 at the 14
th
generation. The Wheel reaches
this threshold at the 27
th
generation and the
Tournament does not reach it within the first 50
generations.
But the BT method is a specific method for a large
mutation chance and it performs poorly with a low
mutation chance. As you can observe with the figure
2, where we set M
c
= 0.1 and M
r
= 0.8:
Figure 2: Comparison of reproduction with a low mutation.
0
0,01
0,02
0,03
0,04
0,05
1 5 9 13 17 21 25 29 33 37 41 45 49
BestLogLoss
No.ofgeneration
Tournament BT Wheel
Genetic Algorithm as Machine Learning for Profiles Recognition
161

4 RESULTS
The real test of our algorithm will be done in a
supervised machine learning context. It will be
evaluated for the quality of its predictions.
For that, we trained our model with the GA
presented in (Section 3) over a training set composed
of 3,003 similarities between profiles. In the training
set, an output for a similarity between two profiles is
either 1 (the two profiles correspond to the same
person) or 0. Apart from the training set, we have a
test set, composed with 741 similarities and their
output with the same format. This set is not used to
train the model with the GA; its only purpose is to
evaluate predictions for our trained model.
These sets are extracted from different sources.
Therefore, each set is really disparate because its
contain profiles with different size.
Figure 3: Distribution of the profiles in the training set.
The distribution of profiles, in the training set,
according to the number of information per profile is
as follows:
Within the training set, the average information
per profile is 14.49 but the standard deviation is
11.13. This standard deviation is really high
compared with the average, which proves the
diversity in the training set. Even if the test set is
smaller, its average is 14.57 and its standard deviation
is 11.08, which is almost the same diversity as the
training set.
During our training phase, our model learns from
a dataset with discrete outputs. But as we are using a
mathematical model (described in section 2) based on
cosine to compute similarity rate, the outputs are
continuous values.
Therefore, this section will present how our model
performs on this test set viewed from two aspects:
regression problem and classification. The former
will evaluate our original model to predict continuous
valued output, corresponding to the similarity rate
between two profiles. The second will adapt our
model to determine if either two profiles are similar
(class = 1) or non-similar (class = 0).
4.1 Regression Problem
In our case, the regression problem is translated into
the capacity for our model to determine that some pair
of profiles are more similar than others, even if all
these pairs correspond to the same person (output =
1). The differences between similarity rates come
from the fact that, even for a human, deducing that 2
profiles correspond to the same person is more
obvious with some data than others.
But we cannot objectively evaluate the similarity
score computed by our model. Imagine that, for a
specific pair of profiles, our model sets up a similarity
score at 0.7. As humans, a value of 0.7 has no
meaning when it comes to decide whether two
profiles concern the same person, or two. We expect
“yes” or “no”. For our model, 0.7 makes sense from
a computational point of view.
Actually, what we really need is to find clusters of
profiles which correspond to the same person.
In our test set, we have the following clusters:
Figure 4: Clusters within the test set.
Each node represents a profile and each link
represents a similarity between 2 profiles (output =
1). The cluster 1 – 2 – 3 means that each profile is
related to the same real person.
Our model predicted the following clusters:
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
162
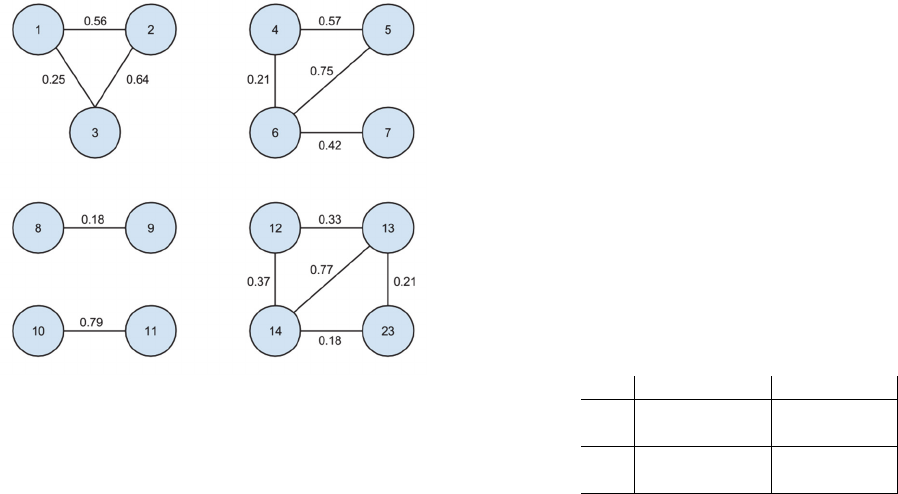
Figure 5: Clusters prediction.
Each value matched with a link corresponds to a
similarity value between 2 profiles. We removed the
links with a 0 value.
The first observation is that each cluster is there,
even if some links (5-7, 4-7 and 12-23) are missing.
This means that the model allows us to indirectly link
profiles which are not similar with the direct
comparison of their data.
We can also observe an expected pattern with the
first cluster (1-2-3), where the links 1-2 and 2-3 have
strong similarities while the link 1-3 is weak. Indeed,
when we look closer at the test set, the profile 2
contains more relevant information than both profiles
1 and 3. Therefore, this is really positive that our
model is also able to detect both strong and weak
similarities.
4.2 Binary Classification
For binary classification, we need our model to be
able to classify two profiles as similar (class 1,
positive class) or non-similar (class 0, negative class).
4.2.1 Threshold
In order to allow our model to classify two profiles,
we need to set up a threshold. Two profiles with a
predicted value below this threshold will be classified
as the class 0, otherwise as the class 1.
As part of the learning phase, this threshold shall
be tuned so as to match user’s expectation about the
model. A high threshold should be used if the user
wants his model to be restrictive to determine that two
profiles are similar and, in return, a low threshold for
an extendible model is needed.
To give an example, in the context of our project,
we fixed the threshold to 0.075 because we presume
that two profiles are similar when some relevant
information match.
4.2.2 Metrics
First of all, we need to define the different metrics
widely used in binary classification problems.
In binary classification, a model predicts if a data
has a class 0 or 1 (predicted class) and a dataset
indicate the actual class for this data.
Then, we can introduce 4 metrics as follow:
Table 5: Main metrics for binary classification.
Actual Class
1 0
Predicted
Class
1 True positive False
positive
0 False
negative
True
negative
In general, positive = identified and negative =
rejected. Therefore:
True positive (TP) = correctly identified
False positive (FP) = incorrectly identified
True negative (TN) = correctly rejected
False negative (FN) = incorrectly rejected
Usually, a metric accuracy is used and defined as:
⁄
(9)
where M = size of the dataset.
But in our case it will not be relevant because we
can define our class 1 as a skewed class. Our training
set is composed with 3003 similarities but only 26 of
them (0.87%) have an output of 1. It means that if a
model predicts always the class 0, it would have an
accuracy of 99.13%.
Therefore, a binary classification problem with a
skewed class is defined as an imbalanced learning
problem and it should be handled specially (He &
Garcia, 2009). Then, we would use other metrics such
as precision (P) and recall (R). Precision is defined as
follows:
⁄
(10)
This metrics is useful to evaluate how well a
model predicts positives values.
The recall (R) is defined as follows:
⁄
(11)
This metric, also named sensitivity, measures the
rate of a model to predict incorrect positives classes.
Genetic Algorithm as Machine Learning for Profiles Recognition
163
These two metrics are really useful but there is an
issue: they are interdependent.
Supposing that we want the model to predict that
two profiles are similar only if it is very confident (i.e.
avoid false positives). Then, we would fix the
threshold to a high value, like 0.9. Doing so, the
model will have a higher precision and a lower recall.
On the contrary, considering we would like a
model which avoid missing similarities between
profiles (i.e. avoid false negatives). This time, we
would fix the threshold to a low value, like 0.1. The
result will be a higher recall and a lower precision.
Now, the problem is that we need a good metric
that will help to find a balance between precision and
recall. As an illustration, considering the following
table:
Table 6: Use of Average to compare Precision and Recall.
Precision Recall Average
0.5 0.4 0.45
0.7 0.1 0.4
0.02 1.0 0.51
Genuinely, the first pair (0.5, 0.4) seems better
than the last pair (0.02, 1.0) which is unbalanced. But
the first pair has a worse average than the last pair.
To prevent that, we introduce a last metric, the F1-
Score, as follows:
12
⁄
(12)
This metric is a weighted average of the precision and
recall and we will use this one to measure our test
accuracy.
To show its effectiveness, we updated the table
above with this new metric:
Table 7: Comparison of the Average and F1Score.
Precision Recall Average F1Score
0.5 0.4 0.45 0.444
0.7 0.1 0.4 0.175
0.02 1.0 0.51 0.0392
The F1Score, as well as the other metrics, reaches
its best at value 1 and worst score at 0.
For our test set, we tried different values for the
threshold:
Figure 6: Precision, Recall and F1Score within the test set.
Considering this figure, the first information is that
our model is highly precise. From a low threshold
(0.075) to the highest prediction within the test set
(0.79), the metric precision is always at 1. This level
of precision allows to select a low threshold. This low
threshold also permits to keep a high value for the
metric recall, which gets lower when the threshold
rises.
4.2.3 ROC Curve
In binary classification, a Receiver Operation
Characteristic (ROC) curve is a statistical tool for
evaluating a classifier and choosing a threshold. In
particular, it is fundamental in medicine to determine
a cutoff value for a clinical test (Campbell & Zweig,
1993).
The curve is created by plotting the true positive
rate in function of the false positive rate at various
threshold settings. In Machine Learning, the true
positive rate is the metric called recall and the false
positive rate is named fall-out. The fall-out is defined
as follows:
⁄
(13)
A high threshold would decrease both fall-out and
recall. However, the objective is to get the highest
recall and the lowest fall-out. Indeed, a test with
perfect discrimination has a ROC curve that passes
through the point (0,1) which is called a perfect
classification. Therefore, the closer the curve is to the
upper left corner, the higher the overall accuracy of
the test (Campbell & Zweig, 1993).
The graphical plot of the ROC curve for our test
set is as follows:
0
0,025
0,075
0,125
0,175
0,25
0,35
0,45
0,55
0,65
0,75
0,85
0
0,2
0,4
0,6
0,8
1
Threshold
Value
F1Score Precision Recall
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
164

Figure 7: ROC curve within the test set.
The linear line from the point (0,0) to the point (1,1)
corresponds to a random classification and is called
the line of no-discrimination.
The elbow of the curve (i.e. the best trade-off
point) is explicit and correspond to our selected
threshold of 0.75. The curve for our classifier is really
close to the perfect classification which proves the
high accuracy of our model.
5 CONCLUDING REMARKS
In this paper, we proposed and developed a machine
learning algorithm based on a genetic algorithm for
profiles recognition. Our solution is a combination
between natural language processing, evolutionary
algorithm and surpervised machine learning.
First, we recalled how to represent a profile in a
Vector Space Models, in order to ease the processing
of semantic data.
In a second part, the principle of genetic
algorithms is described; and used to train the
computer to evaluate the significance of each label.
This phase still requires human intervention throught
a training set.
Finally, we tested the model predictions within a
complete new dataset. These predictions revealed a
highly precise model.
Our model allowed to automatically determine
both a similarity score between profiles and which
profiles correspond to the same person.
The solution proposed in this paper is adaptable
and generic. This adaptation is due to the fact that the
model is not restricted to a fixed set of labels. As long
as the labels are present into the training set, both the
mathematical model and the genetic algorithm would
adapt to a new set of labels.
Therefore we strongly believe it could be used for
any kind of sources containing profiles. Moreover,
this solution could also be used to other applications
of similar data recognition.
ACKNOWLEDGEMENTS
We are thankful to Michel Bordry for his help during
the manuscript review. We also thank Andréa
Duhamel for her insightful comments.
REFERENCES
A. K. Jain, M. M. P. F., 1999. Data Clustering: A Review.
ACM Computing Surveys (CSUR), Volume 31, pp. 264-
323.
Campbell, G. & Zweig, M. H., 1993. Receiver-Operation
Characteristic (ROC) Plots: A Fundamental Evaluation
Tool in Clinical Medicine. Clin Chem, 39(4), pp. 561-
577.
Dasarathy, B. V., 1991. Neared neighbor (NN) Norms: NN
Pattern Classification Techniques. IEEE Computer
Society Press.
Eberhart, R. C., Simpson, P. K. & Dobbins, R., 1996.
Computational Intelligence PC Tools. s.l.:AP
Professional.
Goldberg, D. E., 1989. Genetic Algorithms in Search,
Optimization, and Machine Learning. Boston, MA,
USA: Addison-Wesley Longman Publishing Co., Inc.
He, H. & Garcia, E. A., 2009. Learning from Imbalanced
Data. IEEE Transactions on Knowledge and Data
Engineering, Volume 21, pp. 1263-1284.
Holland, J. H., 1992. Adaptation in natural and artificial
systems. Cambridge, MA, USA: MIT Press.
Hüe, X., 1997. Genetic Algorithms for Optimisation :
Background and Applications. s.l.:s.n.
Kim, H. & Cho, S., 2000. Application of interactive genetic
algorithm to fashion design. Engineering Applications
of ArtiÆcial Intelligence.
Kluwer Academic Publishers, 2001. Genetic Algorithms
and Machine Learning. Machine Learning.
Miller, B. L. & Goldberg, D. E., 1995. Genetic Algorithms,
Tournament Selection, and the Effects of Noise.
Complex Systems, Issue 9, pp. 193-212.
Moorhead, P. S. & Kaplan, M. M., 1967. Mathematical
challenges to the neo-Darwinian interpretation of
evolution. Wistar institute symposium monograph,
Issue 5.
Rawashdeh, A. & Ralescu, A. L., 2014. Similarity Measure
for Social Networks - A Brief Survey.
Resende, M. G., 2010. Biased Random-key genetic
00,51
0
0,2
0,4
0,6
0,8
1
FallOut
Recall
RandomClassification
OurClassification
PerfectClassification
Genetic Algorithm as Machine Learning for Profiles Recognition
165
algorithms with applications in telecommunications.
AT&T Labs Research Technical Report.
Salton, G., 1968. Automatic Information Organization and
Retrieval.
Shen, Y., 2005. Loss Functions for Binary Classification
and Class Probability Estimation, s.l.: University of
Pennsylvania.
Srinivas, M. & Patnaik, L. M., 1994. Adaptive Probabilities
of Crossover and Mutation in Genetic Algorithms.
IEEE Transactions on systems, man and cybernetics,
Volume 24, pp. 656-667.
Turney, P. D. & Pantel, P., 2010. From Frequency to
Meaning : Vector Space Models of Semantics. Journal
of Artificial Intelligence Research.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
166
