Application of Adaptive Differential Evolution for Model Identification in
Furnace Optimized Control System
Miguel Leon
1
, Magnus Evestedt
2
and Ning Xiong
1
1
Innovation, Design and Tecnology Department, Malardalen University, Vasteras, Sweden
2
Industrial Systems, Prevas, Vasteras, Sweden
Keywords:
Differential Evolution, Optimization, Model Identification, Temperature Estimation.
Abstract:
Accurate system modelling is an important prerequisite for optimized process control in modern industrial
scenarios. The task of parameter identification for a model can be considered as an optimization problem
of searching for a set of continuous parameters to minimize the discrepancy between the model outputs and
true output values. Differential Evolution (DE), as a class of population-based and global search algorithms,
has strong potential to be employed here to solve this problem. Nevertheless, the performance of DE is
rather sensitive to its two running parameters: scaling factor and crossover rate. Improper setting of these
two parameters may cause weak performance of DE in real applications. This paper presents a new adaptive
algorithm for DE, which does not require good parameter values to be specified by users in advance. Our
new algorithm is established by integration of greedy search into the original DE algorithm. Greedy search
is conducted repeatedly during the running of DE to reach better parameter assignments in the neighborhood.
We have applied our adaptive DE algorithm for process model identification in a Furnace Optimized Control
System (FOCS). The experiment results revealed that our adaptive DE algorithm yielded process models
that estimated temperatures inside a furnace more precisely than those produced by using the original DE
algorithm.
1 INTRODUCTION
System modelling and identification provide an im-
portant basis for optimized process control in modern
industrial scenarios. Its main goal is to identify a pro-
cess model that is able to accurately predict the output
of a system in response to a set of inputs. Generally,
a process model can be constructed in two steps. In
the first step, the structure of the model is determined
in terms of expert knowledge and insight into the pro-
cess. In the second step, the parameters of the struc-
tured model are to be identified. This can be consid-
ered as an optimization problem of searching for a set
of continuous parameters to minimize the discrepancy
between the model outputs and true output values on
a set of training samples.
Traditionally, the methods such as Least Mean
Square (LMS) algorithm or Recursive Least Square
Estimation (RLS) algorithms have been used to solve
the model parameter identification problems. How-
ever, they are subject to two limitations. First, they
were developed for linear system identification, i.e.
when the process model is assumed to be linear. Sec-
ond, they are essentially derivative-based optimiza-
tion techniques and may fail to find the optimal solu-
tion when locating many (model) parameters in high
dimensional spaces.
This paper advocates the application of Differ-
ential Evolution (DE) (Storn and Price, 1997) algo-
rithms to solve the parameter identification problems
for nonlinear process models. DE presents a class
of evolutionary computing techniques that perform
population-based and beam search, thereby exhibit-
ing strong global search ability in complex, non-linear
and high dimensional spaces (Xiong et al., 2015). DE
differs from many other evolutionary algorithms in
that mutation in DE is based on differences of pair(s)
of individuals randomly selected. Thus, the direction
and magnitude of the search is decided by the distri-
bution of solutions instead of a pre-specified probabil-
ity density function. The merits of DE include simple
and compact structure, easy use, as well as high con-
vergence speed, which make it quite competitive in
comparison with other evolutionary algorithms.
However, in real applications, the performance of
DE is largely dependent on the values of scaling factor
48
Leon, M., Evestedt, M. and Xiong, N..
Application of Adaptive Differential Evolution for Model Identification in Furnace Optimized Control System.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 48-54
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

and crossover rate, which are two important control
parameters of DE. Improper setting of such parame-
ters will lead to low quality of solutions found by DE.
Yet finding suitable values for them is by no means a
trivial task, it involves a trial-and-error procedure that
is time consuming.
In this paper we present a new adaptive algorithm
for DE, which does not require good parameter val-
ues (scaling factor and crossover rate) to be specified
by users beforehand. Our new algorithm is estab-
lished by integration of greedy search into the original
DE algorithm. Greedy search is conducted repeatedly
during the running of DE to reach better parameter
assignments in the neighborhood. So far we have ap-
plied our adaptive DE algorithm for process model
identification in a Furnace Optimized Control System
(FOCS). The experiment results revealed that our al-
gorithm yielded process models that estimated tem-
peratures inside a furnace more precisely than those
produced by using the original DE algorithm.
The remainder of the paper is organized as fol-
lows. Section 2 briefly describes the application sce-
nario. The original DE algorithm is outlined in Sec-
tion 3, which is followed by the new adaptive DE al-
gorithm in Section 4. Section 5 presents the results
of experiments for model identification in a Furnace
Optimized Control System. Section 6 discusses some
relevant works. Finally, concluding remarks are given
in Section 7.
2 PROBLEM FORMULATION
Energy consumption and environmental considera-
tion are important issues to be handled within the
steel industry today. In this respect, inventing and
developing new ways to decrease fuel and emission
levels in steel production and treating are crucial to
production economy. The FOCS system was devel-
oped for reheating furnaces in the early 1980s, and
has since grown to be the most commonly used sys-
tem in the Scandinavian steel industry, (Norberg and
Leden, 1988).
Due to the harsh environment inside the reheating
furnace, the temperature of the heated steel cannot be
measured continuously. Therefore, the FOCS system
core is a temperature calculation model that utilizes
temperature sensor measurements in the walls inside
the furnace as well as current fuel flow, to estimate the
temperature in the heated material. In order to gain
optimal control performance, it is crucial to estimate
the temperatures accurately.
The temperature inside the material can be mea-
sured through the furnace by a test measurement
setup. This is normally done 2-3 times every year to
certify the furnace operation. The measurements are
also used to calibrate the FOCS temperature calcula-
tion model, by changing the model parameters to fit
the model output to the measurements. The calibra-
tion is performed manually and can be a tedious task
due to many parameters and evaluation of several test
measurements simultaneously.
We attempted to apply DE algorithms to facilitate
the automatic determination of the parameters of this
process model. The goal is to find such a set of pa-
rameters to minimize the error between the estimated
temperatures from the model and the actual tempera-
tures obtained from the measurements. After the ex-
ecution of DE, we acquire the optimal parameters of
the model, as shown in Fig.1. Subsequently this op-
timal model can be employed in future occasions to
produce reliable estimates of temperatures based on
input conditions.
Figure 1: DE, parameterized model, and temperature esti-
mation.
3 DIFFERENTIAL EVOLUTION
The DE algorithm proposed by R. Storn and K. Price
in 1997 (Storn and Price, 1997) is an stochastic and
population based evolutionary algorithm for global
numerical optimization. The population is compose
by N
P
individuals, solutions of the problem, repre-
sented by X
i,G
= {x
i,1
, x
i,2
, . . . , x
i,D
}, where i =1, 2,. . . ,
N
P
and represents the ith individual, D is the dimen-
sion of the problem and G stands for the generation
that the population belong. DE has three main op-
erators at every generation G: mutation, crossover
and selection. The notation used to name them is
DE/x/y/z, where x represents the mutation strategy
used, y is the number of difference of individuals used
in the mutation strategy and z stands for the crossover
method used. Next we shall briefly describe these
three operators used in a basic DE algorithm.
Mutation: In this first step, NP mutant vectors are
created using individuals randomly selected from the
current population. Indeed there are a lot of mutation
Application of Adaptive Differential Evolution for Model Identification in Furnace Optimized Control System
49
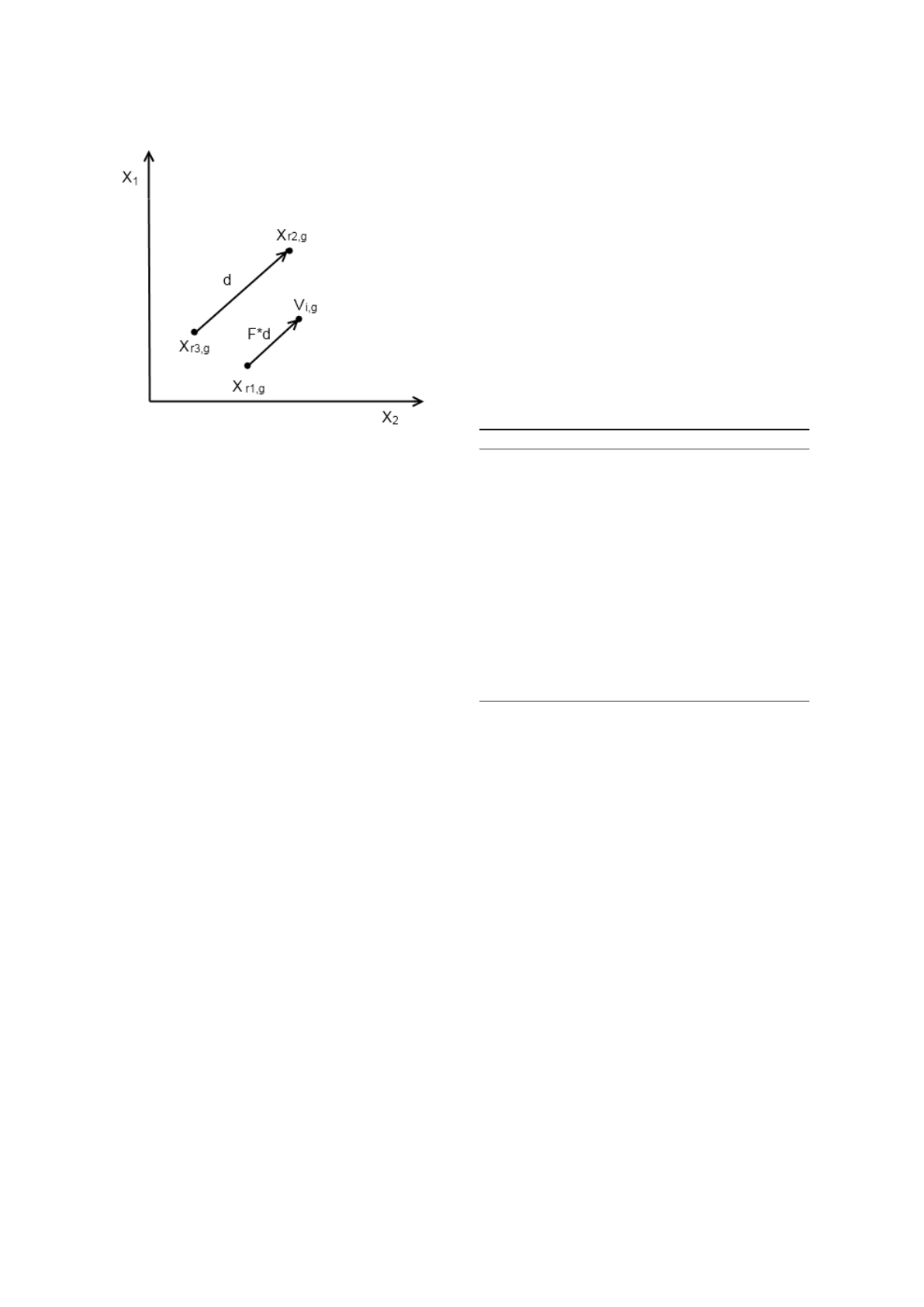
Figure 2: Random mutation with one difference vector.
strategies which can be used to generate mutant vec-
tors. But only the random mutation strategy will be
explained below. The other mutation strategies and
their performance are discussed in (Leon and Xiong,
2014a). The calculation of the mutant vector V
i,G
us-
ing the random mutation strategy is given in Eq.1.1.
V
i,G
= X
r
1
,G
+ F × (X
r
2
,G
− X
r
3
,G
) (1)
where r
1
, r
2
; r
3
are random integers from 1 to N
P
, and
F is the scaling factor inside the interval [0, 2]. Fig.
2 shows how this mutation strategy works, where d is
the difference vector between X
r
2
,G
and X
r
3
,G
.
As can be seen from Eq. 1,, values in the mutant
vector V
i,G
may violate pre-defined boundary con-
straints for the decision variables. To repair such ille-
gal solution (if it emerges), we modify V
i,G
according
to Eq.2.
V
i,G
[ j] =
(
(Low[ j] if V
i,G
[ j] < Low[ j],
(U pper[ j] if V
i,G
[ j] > U pper[ j].
(2)
where V
i,G
[ j] denotes the jth component of vector
V
i,G
, and Low[j] and Upper[j] stand for the low and
upper bounds of the jth decision variable respectively.
Crossover: In this second step, the parent solution
X
i,G
from the current population and the mutant vector
V
i,G
are recombined to create a new solution. This
new solution is called trial vector and it is represented
by T
i,G
. Every parameter inside the trial vector is
generated according Eq. 3. This equation ensures that
T
i,G
is different from X
i,G
in one component at least.
T
i,G
[ j] =
(
V
i,G
[ j] if rand[0, 1] <= CR or j = j
rand
X
i,G
[ j] otherwise
(3)
where j represents the index of every parameter in a
vector, J
rand
is a randomly selected integer between 1
and N
p
and CR is the crossover probability.
Selection: This operation selects the individuals
for the next generation. An individual X
i,G+1
in the
next generation is decided by comparing the fitness
value of the parent X
i,G
and the fitness value of the
trial vector T
i,G
. Therefore, if the problem of interest
is minimization, the individuals in the new generation
are given as follows:
X
i,G+1
=
(
T
i,G
if f (T
i,G
) < f (X
i,G
)
X
i,G
otherwise
(4)
where f denotes the fitness function. The pseudocode
of basic DE is given in Algorithm 1.
Algorithm 1: Differential Evolution.
1: Initialize the population with randomly created
individuals.
2: Calculate the fitness values of all individuals in
the population.
3: while The termination condition is not satisfied
do
4: Create mutant vectors using the random muta-
tion strategy in Eq. 1.
5: Create trial vectors by recombining parents
vectors with mutant vector according to Eq. 3.
6: Evaluate trial vectors with the fitness function.
7: Select the best vectors as individuals in the next
generation according to Eq. 4.
8: end while
4 A NEW DE ALGORITHM WITH
PARAMETER ADAPTATION
As is stated above that the scaling factor (F) and
crossover rate (CR) are two important running param-
eters for DE that significantly affect the optimization
performance. It is also recognized that the proper
value of F may change with time in the evolution-
ary process, while the crossover probability CR is
more dependent on the characteristics of the under-
lying problem. Therefore we aim to develop a new
DE algorithm with parameter self-adaptation. This is
achieved by incorporating greedy local search to dy-
namically adjust the F and CR values during the run-
ning of DE. In the following we shall first outline the
greedy search scheme for parameter adaption in Sub-
section 4.1. Subsequently, the evaluation of parameter
assignments to support the greedy search is discussed
in Subsection 4.2. Finally we outline our adaptive DE
algorithm as a whole in Subsection 4.3.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
50

4.1 Greedy Search for Parameter
Adaptation
We use greedy search to adjust the values of parame-
ters in every learning period, which consists of a spec-
ified number of generations of the evolutionary pro-
cess. The basic idea is to find the best candidate for
parameter assignment in the local neighbourhood of a
current candidate. Hence, in each learning period, the
current candidate and its two neighbouring ones are
examined for their quality, and the best neighbouring
candidate replaces the current one if it is assessed to
be better than the current one. Then the search moves
on to the next learning period. A description of the
greedy search scheme designed for parameter adapta-
tion is given below:
The general greedy search scheme for parameter
adaptation:
1. Set the index fo the first learning period LP = 1.
2. C = initial candidate for parameter assignment
3. Expand C: creating two neighbouring candidates
C
1
and C
2
as children of C
4. Evaluate the quality of the three candidates C, C
1
and C
2
for parameter assignment
5. Let C
∗
be the best one from C
1
and C
2
6. C = C
∗
If C
∗
is superior to C
7. LP = LP + 1 and go to Step 3
It is important to note that the above greedy search
scheme does not terminate when no better candidate
can be found in the neighborhood. Instead the search
always continues from one learning period to another
to achieve continuous adaptation of parameters during
the execution of the DE algorithm.
4.2 Evaluation of Candidates for
Parameter Assignment
The implementation of the greedy search scheme de-
scribed above entails reliable assessment of candi-
dates for DE parameter assignment. Owing to the
stochastic operations in DE, an assignment of param-
eters has to be tested by applying it with a number of
times. We desire those parameter assignments that not
only offer a high chance of survival for trial solutions
but also enable substantial improvement of fitness in
the next generation.
Lets now consider a candidate Z
P
and assume that
Z
P
has been tested N times by using it to produce trial
solutions. Let X
j
and V
j
be the parent and trial solu-
tions respectively in the jth test of Z
P
. The relative
improvement (for a minimization problem) from this
test is defined as
RI(C, j) =
(
f (X
j
) ∗ 10
n
− f (V
j
) ∗ 10
n
, i f f (X
j
) ≥ f (V
j
),
0, otherwise.
(5)
where f is the objective function and n is an integer
such that f (V
j
) ∗ 10
n
lies in the interval [1,10].
The progress rate (PR) for Z
P
is the average of the
relative improvements from all the N tests, thus we
have
PR(Z
P
) =
1
N
N
∑
j=1
RI(Z
P
, j) (6)
The progress rate defined in 6 is used as the mea-
sure to assess candidates for parameter assignment in
the greedy search.
4.3 Adaptive DE Algorithm with
Greedy Search
The Adaptive Differential Evolution algorithm is de-
veloped by incorporation of the greedy search mech-
anism into the basic DE algorithm. The whole evolu-
tionary process is divided into a sequence of learn-
ing periods and every learning period consists of a
fixed number of generations. The greedy search is
performed in successive learning periods to facilitate
continuous and dynamic adjustment of F and CR val-
ues during the execution of the algorithm.
The initial candidate for mutation factor is set as
F = 0.5, and its two neighbours are F +C
1
and F −C
1
respectively, where C
1
is a user specified small posi-
tive number. The initial candidate for crossover rate
is a Cauchy distribution with its centre being CR
m
=
0.5 and its scale parameter equal to 0.2. The two
neighbours of this current distribution are the shifted
Cauchy distributions with their centres being located
at CR
m
+C
2
and CR
m
−C
2
respectively, where C
2
is
a small positive number specified by user. Every cur-
rent and neighbouring candidate (for both the scaling
factor and crossover rate) receives a probability of 1/3
to be associated with an individual vector in the pop-
ulation in order to get a sufficient number of usages
(tests) in the learning period. At the end of the learn-
ing period, a neighbouring candidate may replace the
current one as a result of the comparison of the as-
sessed progress rates.
A more detailed description of our method is
given in the pseudocode of Algorithm 2.
Application of Adaptive Differential Evolution for Model Identification in Furnace Optimized Control System
51

Algorithm 2: Adaptive DE Algorithm with Greedy Search.
1: Set CR
m
= 0.5, F = 0.5, LP = 20, d
1
= d
2
= 0.01;
2: Z
F
= {F −d
1
, F, F +d
1
};
3: Z
CR
= {CR
m
− d
2
,CR
m
,CR
m
+ d
2
};
4: Initialize the population with randomly created
individuals.
5: Evaluate the population.
6: G = 1;
7: while The termination condition is not satisfied
do
8: for i = 1 to N
P
do
9: Set F
i
by randomly selecting one element
from Z
F
.
10: Set µ
CR
by randomly selecting one element
from Z
CR
.
11: CR
i
= Cauchy(µ
CR
, 0.2).
12: Create the mutant vector using the mutation
strategy given in Equation 1
13: Repair the mutant vector if it has values out-
side the boundaries, using Equation 2.
14: Create the trial vector by recombining the
mutant vector with the parent vector accord-
ing to Equation 3.
15: Evaluate the trial vector with the fitness
function.
16: Select the winning vector according to
Equation 4 as the individual in the next gen-
eration.
17: end for
18: if G%LP == 0 then
19: F = best(Z
F
).
20: Z
F
= {F −d
1
, F, F +d
1
};
21: CR
m
= best(Z
CR
).
22: Z
CR
= {CR
m
− d
2
,CR
m
,CR
m
+ d
2
};
23: end if
24: G = G + 1;
25: end while
5 EXPERIMENTS
The purpose of this section is to examine the capabil-
ity of our adaptive DE algorithm in a real industrial
scenario. We applied our algorithm on the problem
of model identification in FOCS and then compared
its results with those obtained by using the basic DE
algorithm on the same problem.
5.1 Experimental Settings
Our adaptive DE algorithm and basic DE were tested
in the experiments for comparison. Both algorithms
use the binomial crossover operator, and both have
three important running parameters: population size
(NP), crossover rate (CR) and mutation factor (F).
The parameters adopted for the basic DE are: N
P
=
60, CR = 0.5 and F = 0.5. The parameters used in our
adaptive algorithm are: N
P
= 60, CR
m
= 0.5, F = 0.5,
C
1
= C
2
= 0.01, and the learning period LP = 3.
The two algorithms were executed 10 times to
solve the model identification problem. The maxi-
mal number of evaluations was set to a relatively low
amount 2000, due to the high computational cost in
fitness evaluations.
5.2 Comparing Our Adaptive with
Basic DE
The errors of the process models found by the two al-
gorithms in the 10 executions are listed in Table 1 for
comparison. In the table we also see the best, mean
and worst errors from the 10 executions for each of
the algorithms.
Table 1: Errors of the models from the two algorithms.
Execution DE GADE
Exec 1 277.6 224.8
Exec 2 242.8 259.7
Exec 3 250.8 243.9
Exec 4 274 247
Exec 5 266.1 243.5
Exec 6 281.8 237.9
Exec 7 269.2 247.7
Exec 8 275.6 237.8
Exec 9 267.8 235.2
Exec 10 278.2 237.8
MEAN: 268.39 241.53
WORST: 281.8 259.7
BEST: 242.8 224.8
Table 2 shows the reduction of the mean error
achieved by our adaptive DE algorithm: the reduc-
tions in the absolute value and the percentage.
Table 2: The reduction of error by using our adaptive DE.
Value Percentage
Improvement 26.86 10.01 %
As can be observed from these two tables (Tables
1 and 2), our adaptive DE algorithm outperforms the
basic DE in this industrial problem. The mean error
from our algorithm is 10% smaller than that of the
basic DE, which indicates a significant improvement
in the quality of the acquired solutions.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
52
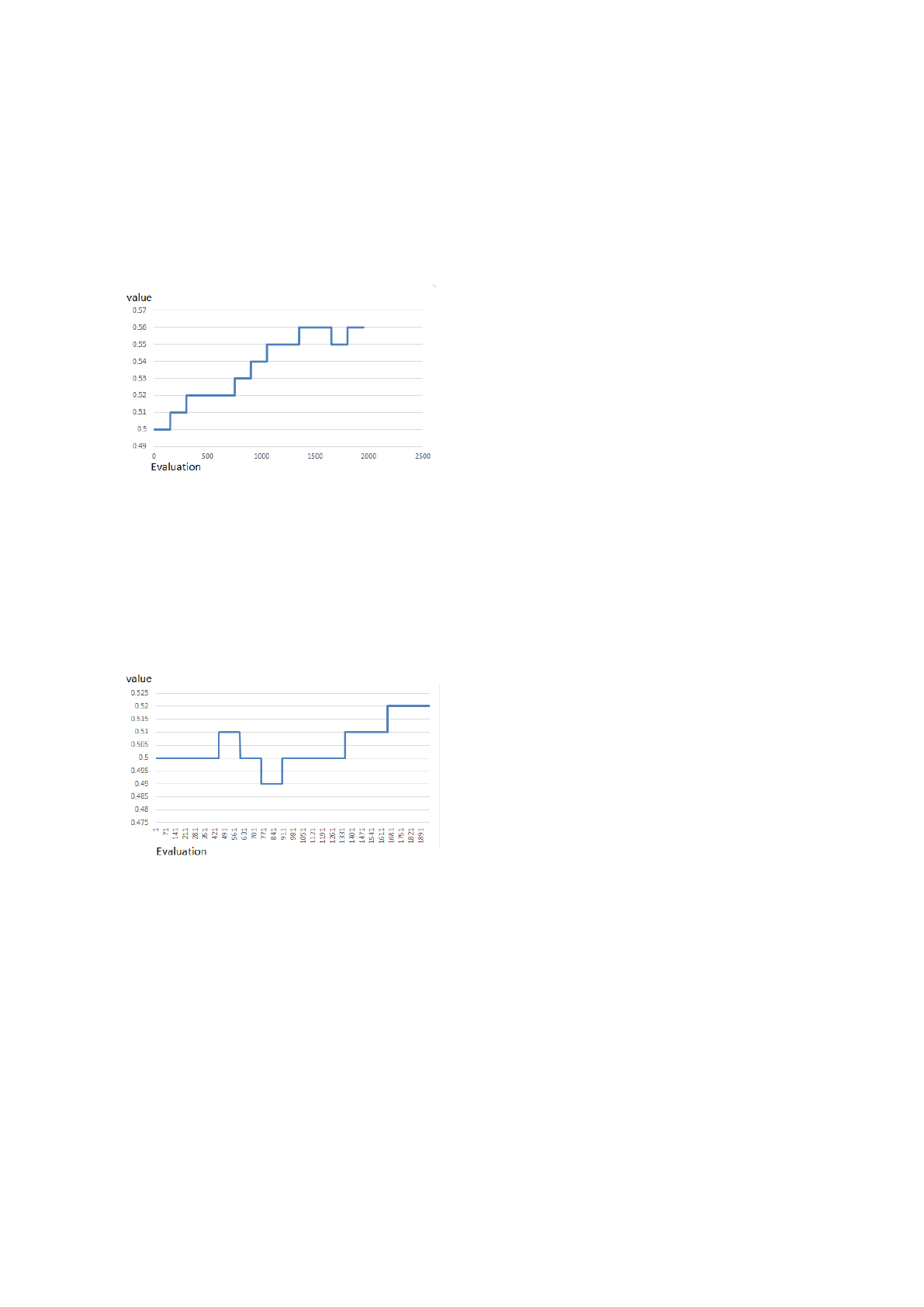
5.3 Evolution of the Parameters
In Fig. 3, we can see the evolution of the scaling fac-
tor (F) during the optimization process. Since the in-
dividuals of the population were similar to each other
at the beginning, the value of F started to increase to
enable big movement in the mutation.
Figure 3: The evolution of the scaling factor F.
In Fig. 4, we can observe the change of the dis-
tribution center (CR
m
) for the crossover probability
during the process. The value of CR
m
increased for
the same reason as stated for the scaling factor F, i.e.,
the individuals in the population were similar to each
other. Hence we needed more elements from the mu-
tant vectors to increase the diversity of the population.
Figure 4: The evolution of the distribution center for the
crossover probability.
6 RELATED WORK
DE has been applied successfully in many real ap-
plications such as system design and parameter opti-
mization. In (Sickel et al., 2007) DE and Fast Differ-
ential Evolution (FDE) were employed to solve two
different problems in Power Plant Control. With the
experiments, the authors showed that DE and FDE
outperformed Particle Swarm Optimization (PSO)
and its variants. In (Bakare et al., 2007) comparisons
were made between DE with PSO in the tasks of re-
active control of the power and voltage. The con-
clusion from both (Sickel et al., 2007) and (Bakare
et al., 2007) was that DE outperformed PSO, yet with-
out significant superiority. In (Mohanty et al., 2014)
the authors employed DE in the applications of load
frequency control of a multi-source power system.
They proposed the application of DE to optimize P, PI
and PID controllers. However, the running parame-
ters of DE were tuned manually with a trial-and-error
method to achieve good optimization performance.
The main problem with applying DE to solve
practical problems lies in the parameter setting. Very
often domain engineers do not have that knowledge to
decide which parameters to choose for DE. Therefore
it is an appealing idea to enhance DE with some abil-
ity of self-adapting its parameters. The direction of
research has received some efforts recently. In (Gong
and Cai, 2014) multi-strategy adaptive differential
evolution was proposed to locate the best parame-
ters for the model of the proton exchange membrane
fuel cell. Zou et al. (Zou et al., 2011) proposed an
improved Differential Evolution (IDE) with an adap-
tive mutation factor and a dynamical crossover rate
to solve the task assignment problem. In (Mulumba
and Folly, 2012) Self-Adaptive Differential Evolution
(SADE) was used to tune the parameters of a power
system stabilizer (PSS).
7 CONCLUSION
This paper shows that Differential Evolution (DE)
algorithms can be applied successfully to solve the
problem of parameter identification in process model-
ing. This is implemented by utilizing DE as a power-
ful global search mechanism to discover best parame-
ters of the model to minimize the difference between
model outputs and true measurement values. Further,
we present a new adaptive DE algorithm that exhibits
two attractive properties for real applications. First,
it does not require prior knowledge about the good
values of the scaling factor and crossover rate for DE.
Second, it enables self-adaptation of these two param-
eters during the running of DE. Case study has been
done of applying this algorithm within the context of
the Furnace Optimized Control System. The results
of the experiments indicate that our new adaptive DE
algorithm outperformed the original DE by yielding
higher accuracy of the models produced.
For future work, we plan to enhance our adaptive
DE algorithm with a more advanced mutation strat-
egy. We also intend to incorporate local search such
as Simplex, Quasi Newton method or some Random
Application of Adaptive Differential Evolution for Model Identification in Furnace Optimized Control System
53
local search methods (Leon and Xiong, 2014b) (Leon
and Xiong, 2015) into the current adaptive DE algo-
rithm. At last, more case studies will be made to ex-
amine our work in more industrial scenarios.
ACKNOWLEDGEMENTS
The work is supported by the Swedish Knowledge
Foundation (KKS) grant (project no 16317).
REFERENCES
Bakare, G., Krost, G., Venayagamoorthy, G., and Aliyu,
U. (2007). Comparative application of differential
evolution and particle swarm techniques to reactive
power and voltage control. In International Confer-
ence on Intelligent Systems Applications to Power Sys-
tems, 2007. ISAP 2007. Toki Messe, Niigata, pages 1–
6.
Gong, W. and Cai, Z. (2014). Parameter optimization of
pemfc model with improved multi-strategy adaptive
differential evolution. Engineering Applications of Ar-
tificial Intelligence, 27:28–40.
Leon, M. and Xiong, N. (2014a). Investigation of mutation
strategies in differential evolution for solving global
optimization problems. In Artificial Intelligence and
Soft Computing, pages 372–383. springer.
Leon, M. and Xiong, N. (2014b). Using random local
search helps in avoiding local optimum in diefferential
evolution. In Proc. Artificial Intelligence and Applica-
tions, AIA2014, Innsbruck, Austria, pages 413–420.
Leon, M. and Xiong, N. (2015). Eager random search for
differential evolution in continuous optimization. In
Progress in Artificial Intelligence, pages 286–291.
Mohanty, B., Panda, S., and PK, H. (2014). Controller
parameters tuning of differential evolution algorithm
and its application to load frequency control of multi-
source power system. International journal of electri-
cal power & energy systems, 54:77–85.
Mulumba, T. and Folly, K. (2012). Application of self-
adaptive differential evolution to tuning pss parame-
ters. In Power Engineering Society Conference and
Exposition in Africa (PowerAfrica), 2012 IEEE, Jo-
hannesburg, pages 1–5.
Norberg, P. and Leden, B. (1988). New developments of
the computer control system focs-rf - application to
the hot strip mill at ssab, domnarvet. SCANHEATING
II, pages 31–60.
Sickel, J. V., Lee, K., and Heo, J. (2007). Differential evo-
lution and its applications to power plant control. In
International Conference on Intelligent Systems Ap-
plications to Power Systems, 2007. ISAP 2007., Toki
MEsse, Niigata, pages 1–6. IEEE.
Storn, R. and Price, K. (1997). Differential evolution - a
simple and efficient heuristic for global optimization
over continuous spaces. Journal of Global Optimiza-
tion, 11(4):341 – 359.
Xiong, N., Molina, D., Leon, M., and Herrera, F. (2015).
A walk into metaheuristics for engineering optimiza-
tion: Principles, methods, and recent trends. Interna-
tional Journal of Computational Intelligence Systems,
8(4):606–636.
Zou, D., Liu, H., Gao, L., and S.Li (2011). An improved dif-
ferential evolution algorithm for the task assignment
problem. Engineering Applications of Artificial Intel-
ligence, 24:616–624.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
54
