Dynamic Feature Selection with Wrapper Model and Ensemble
Approach based on Measures of Local Relevances and Group Diversity
using Genetic Algorithm
Marek Kurzynski, Pawel Trajdos and Maciej Krysmann
Department of Systems and Computer Networks, Wroclaw University of Technology,
Wyb. Wyspianskiego 27, 50-370, Wroclaw, Poland
Keywords:
Feature Selection, Feature Relevance, Diversity of Feature Ensemble, Genetic Algorithm.
Abstract:
In the paper the novel feature selection method, using wrapper model and ensemble approach, is presented.
In the proposed method features are selected dynamically, i.e. separately for each classified object. First,
a set of identical one-feature classifiers using different single feature is created and next the ensemble of
features (classifiers) is selected as a solution of optimization problem using genetic algorithm. As an optimality
criterion, the sum of measures of features relevance and diversity of ensemble of features is adopted. Both
measures are calculated using original concept of randomized reference classifier, which on average acts like
classifier with evaluated feature. The performance of the proposed method was compared against six state-
of-art feature selection methods using nine benchmark databases. The experimental results clearly show the
effectiveness of the dynamic mode and ensemble approach in feature selection procedure.
1 INTRODUCTION
In the past three decades, the feature selection (FS)
methods havebeen studied intensivelyin the literature
of machine learning and pattern recognition (Chan-
drashekar and Sahin, 2014). The aim of FS is to
choose a small subset of the relevant features from
the original ones according to adopted relevance eval-
uation criterion, which usually leads to better learn-
ing performance, i.e. higher accuracy of classifica-
tion, lower computational cost, and better model in-
terpretability.
The existing FS algorithms generally can be
grouped into three categories: supervised, unsuper-
vised, and semi-supervised FS. The supervised FS
methods, which select features according to labeled
training data, can further be broadly categorized into
three groups: filter models, wrapper models and em-
bedded models (Guyon and Elisseeff, 2003).
The filter methods choose important features by
evaluating different models of relation (consistency,
dependency, information, correlation) between indi-
vidual feature and class labels, without involving any
learning algorithm (classification method). A typical
filter algorithm consists of two steps. In the first step,
each feature is ranked using different criteria for FS,
such as Kolmogorov measure, Bhattacharyya mea-
sure, Machalanobis distance, Shanon entropy, infor-
mation gain to name only a few (Bolon-Canedo et al.,
2012), (Duda et al., 2012). In the second step, features
with the highest rankings are chosen as input data in
the classification model.
The wrapper model uses the classification accu-
racy of a predefined classifier (learning model) to de-
termine the quality of selected features. They often
report better results than filter methods, but at the
price of an increased computational cost. Finally,
the embedded methods use internal information of
the classification model to perform feature selection
(Saeys et al., 2007).
Recently, ensemble methods have been developed
as an effective tool for FS (Saeys et al., 2008). It is
reported, that ensemble feature selection may reduce
the risk of choosing an unstable subset and ensemble
feature selection might give a better approximation to
the optimal subset or ranking of features (Wang et al.,
2010). Similar to the construction of ensemble mod-
els for supervised learning, there are three phases in
creating a feature selection ensemble: generation, se-
lection and integration (fusion) (Kuncheva,2004a). In
the generation phase a set of different feature selec-
tors is created. In the selection phase one or a subset
of these feature selectors is selected from the pool,
and in the integration phase the final set of features is
Kurzynski, M., Trajdos, P. and Krysmann, M..
Dynamic Feature Selection with Wrapper Model and Ensemble Approach based on Measures of Local Relevances and Group Diversity using Genetic Algorithm.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 167-173
ISBN: 978-989-758-157-1
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
167

selected as a fusion of results of selected feature selec-
tors. It must be emphasized that such a representation
is not unique (Lysiak et al., 2014) since the selection
and integration phases may be optional. For instance,
one may find the set of selected features, where all
feature selection methods (feature selectors) are used
without any selection or the set of selected features,
where just one selector from the pool is used, mak-
ing the integration phase unnecessary. Variation in
the generating phase can be achieved by using vari-
ous feature selection methods (e.g. various criteria of
features evaluation in the filter approach). Aggregat-
ing the different feature selection results can be done
by voting, e.g. in the case of deriving a consensus
feature ranking, or by counting the most frequently
selected features in the case of deriving a consensus
feature subset.
In this work, the novel ensemble feature selection
method using wrapper model is proposed, which is
based on dynamic ensemble selection (DES) scheme
(Woloszynski et al., 2012). In the proposed approach,
in the generation phase a set of identical classifiers
using different single features is created. In the selec-
tion phase the ensemble of features (one-feature clas-
sifiers) from the pool is selected, and in the integra-
tion phase the selected features (selected one-feature
classifier) are combined and used for classification of
a test object. According to the DES scheme, the fea-
tures are selected in dynamic mode, i.e. the set of
selected features can be different for different test ob-
jects in contrast to the static mode, where the selected
set of features is the same for all test objects. In the
selection phase, we formulate the optimal feature se-
lection problem adopting the sum of relevance of fea-
tures and diversity of feature ensemble as an optimal-
ity criterion. Since this problem can not be directly
solved using analytical ways, we propose to apply
genetic algorithm (GA), which is very well-known
search heuristic procedure and has been successfully
applied to a broad spectrum of different optimization
problems (Goldberg, 1989). Methods for calculating
measure of feature relevance and measure of diver-
sity of features ensemble are based on the original
concept of a randomized reference classifier (RRC)
(Woloszynski and Kurzynski, 2011), which on aver-
age acts like classifier with evaluated feature.
The paper is organized as follows. In section 2,
the measures of feature relevance and diversity of fea-
ture ensemble using randomized reference classifier
are developed. Furthermore, the optimization prob-
lem is defined and solution based on genetic algo-
rithm is presented. Results of experimental investiga-
tions with statistical verification are presented in sec-
tion 3. Section 4 concludes the paper.
2 DYNAMIC FEATURE
SELECTION
2.1 Preliminaries
Let
f = ( f
(1)
, f
(2)
, . . . f
(L)
), (1)
and
x = (x
(1)
, x
(2)
, . . . x
(L)
), x
(l)
∈ X
(l)
(2)
be a vector of primary features and vector of their
values, respectively. Let ψ
l
(l = 1, 2, . . . L) be a
trained classifier using feature f
(l)
, which maps one-
dimensional feature space into the set of class num-
bers, viz.
ψ
l
: X
(l)
⇒ M = {1, 2, . . . M}. (3)
Classification is made according to the maximum
rule
ψ
l
(x
(l)
) = i ⇔ d
(i)
ψ
l
(x
(l)
) = max
j∈M
d
( j)
ψ
l
(x
(l)
), (4)
where
[d
(1)
ψ
l
(x
(l)
), d
(2)
ψ
l
(x
(l)
), . . . d
(M)
ψ
l
(x
(l)
)] (5)
is a vector of class-supports (classifying functions)
produced by ψ
l
(x
(l)
). The value of d
( j)
ψ
l
(x
(l)
), ( j ∈ M )
represents a support given by the classifier ψ
l
for the
fact that object described by x
(l)
belongs to the jth
class. Without the loss of generality, we assume that
d
( j)
ψ
l
≥ 0 and
∑
j
d
( j)
ψ
l
= 1.
In this study, we propose two measures which are
the basis for dynamic selection of features from the
vector of primary features (1):
1. local (at a point x = (x
(1)
, x
(2)
, . . . x
(L)
)) relevance
measure R( f
(l)
|x) of individual feature f
(l)
. This
measure evaluates the capability of classifier ψ
l
to
correct classification of a test object x;
2. diversity measure D(F
E
|x) of any ensemble of fea-
tures F
E
considered as the independency of the er-
rors made by the classifiers with member features
at a test point x.
In this paper, the trainable relevance and diversity
measures are proposed using probabilistic model. It
is assumed that a validation set
V = {(x
1
, j
1
), (x
2
, j
2
), . . . , (x
N
, j
N
)}, (6)
x
k
∈ X = X
(1)
×, X
(2)
× . . . × X
(L)
, j
k
∈ M
containing pairs of primary features vector and their
corresponding class label is available for the super-
vised learning of relevance and diversity measures.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
168

2.2 Measures of Relevance and Group
Diversity
The concept of a hypothetical classifier called ran-
domized reference classifier (RRC) originally intro-
duced in (Woloszynski and Kurzynski, 2011) is a con-
venient and effective tool for determining both rele-
vance and diversity measures.
A classifier ψ
l
is modeled by a random-
ized reference classifier, which takes decisions
in a random manner. The RRC
l
classifies
object x
(l)
∈ X
(l)
according to the maximum
rule (4) and it is constructed using a vector
of class supports [δ
(1)
l
(x
(l)
), δ
(2)
l
(x
(l)
), . . . , δ
(M)
l
(x
(l)
)],
which are observed values of random variables
[∆
(1)
l
(x
(l)
), ∆
(2)
l
(x
(l)
), . . . , ∆
(M)
l
(x
(l)
)]. Probability dis-
tributions of the random variables satisfy the follow-
ing conditions:
1. ∆
( j)
l
(x
(l)
) ∈ [0, 1],
2. E[∆
( j)
l
(x
(l)
)] = d
( j)
ψ
l
(x(l)), j = 1, 2, . . . , M,
3.
∑
j=1,2,...,M
∆
( j)
l
(x
(l)
) = 1,
where E is the expected value operator. In other
words, class supports produced by the modeled clas-
sifier ψ
l
are equal to the expected values of class sup-
ports produced by the RRC
l
.
Since the RRC performs classification in a
stochastic manner, it is possible to calculate the
probability of classification of an object x =
(x
(1)
, x
(2)
, . . . x
(L)
) to the i-th class:
P
(RRC
l
)
(i|x) =
Pr[∀
k=1,...,M, k6=i
∆
(i)
l
(x
(l)
) > ∆
(k)
l
(x
(l)
)]. (7)
In particular, if the object x belongs to the i-th
class, from (7) we simply get the conditional prob-
ability of correct classification Pc
(RRC
l
)
(x).
The key element in the modeling presented above
is the choice of probability distributions for the ran-
dom variables ∆
( j)
l
(x
(l)
), j ∈ M so that the conditions
1-3 are satisfied. In this paper, the beta probability
distributions are used with the parameters α
( j)
l
(x
(l)
)
and β
( j)
l
(x
(l)
) (j ∈ M ). The justification of the choice
of the beta distribution can be found in (Woloszynski
and Kurzynski, 2011), and furthermore the MATLAB
code for calculating probabilities (7) was developed
and it is freely available for download (Woloszynski,
2013).
Applying the RRC
l
to a validation point x
k
and putting in (7) i = j
k
, we get the probability
of correct classification of RRC
l
at a point x
k
=
(x
(1)
k
, x
(2)
k
, . . . x
(L)
k
) ∈ V , namely:
Pc
(RRC
l
)
(x
k
) = P
(RRC
l
)
( j
k
|x
k
), x
k
∈ V . (8)
Similarly, putting in (7) a class j 6= j
k
, we get the
class-dependent error probability at a point x
k
∈ V :
Pe
(RRC
l
)
( j|x
k
) = P
(RRC
l
)
( j|x
k
), (9)
x
k
∈ V , j(6= j
k
) ∈ M .
Since the RRC
l
can be considered equivalent to the
modeled classifier ψ
l
, it is justified to use the proba-
bility (7) as the relevance measure of feature f
l
at the
validation point x
k
∈ V , i.e.
R(ψ
l
|x
k
) = Pc
(RRC
l
)
(x
k
). (10)
The relevance measure for the validation objects
x
k
∈ V can be then extended to the entire feature
space X
(l)
. To this purpose, the following normal-
ized Gaussian potential function model was used
(Woloszynski and Kurzynski, 2010):
R( f
(l)
|x) =
∑
x
k
∈V
R( f
(l)
|x
k
)exp(−dist(x
(l)
, x
(l)
k
)
2
)
∑
x
k
∈V
exp(−dist(x
(l)
, x
(l)
k
)
2
)
, (11)
where dist(x
(l)
, x
(l)
k
) is the Euclidean distance be-
tween the objects x and x
k
in the space X
(l)
.
The diversity of a feature ensemble F
E
is consid-
ered as an independency of the errors made by classi-
fiers ψ
l
using the member features f
(l)
∈ F
E
. Hence,
the method in which diversity measure is calculated
as a variety of class-dependent error probabilities (9)
is fully justified.
Similarly, as in relevance measure, we assume that
at a validation point x
k
∈ V the conditional error prob-
ability for the class j 6= j
k
of the classifier ψ
l
is equal
to the appropriate probability of the equivalent RRC
l
,
namely:
Pe
(ψ
l
)
( j|x
k
) = Pe
(RRC
l
)
( j|x
k
). (12)
Next, these probabilities can be extended to the
entire feature space X
(l)
using Gaussian potential
function (11):
Pe
(ψ
l
)
( j|x) =
∑
x
k
∈V , j
k
6= j
Pe
(ψ
l
)
( j|x
k
)exp(−dist(x
(l)
, x
(l)
k
)
2
)
∑
x
k
∈V , j
k
6= j
exp(−dist(x
(l)
, x
(l)
k
)
2
)
. (13)
According to the presented concept, with the use
of probabilities (13), first we calculate pairwise diver-
sity at the point x ∈ X for all pairs of features f
(l)
and
f
(k)
(for classifiers ψ
l
and ψ
k
), l, k = 1, 2, . . . L, l 6= k:
D( f
(l)
, f
(k)
|x) =
Dynamic Feature Selection with Wrapper Model and Ensemble Approach based on Measures of Local Relevances and Group Diversity
using Genetic Algorithm
169

1
M
∑
j∈M
|Pe
(ψ
l
)
( j|x) − Pe
(ψ
k
)
( j|x)|, (14)
and finally, we get diversity of ensemble of n (n ≤ L)
features F
E
(n) at a point x ∈ X as a mean (normal-
ized) value of pairwise diversities (14) for all pairs of
member features, namely:
D(F
E
(n)|x) =
2
n· (n − 1)
×
×
∑
f
(l)
, f
(k)
∈F
E
(n);l6=k
D( f
(l)
, f
(k)
|x). (15)
2.3 The Optimal Feature Selection
The proposed dynamic feature selection method
(DFS) is constructed as follows:
1. For a given test object x ∈ X , the relevance mea-
sures (11) are calculated for each feature f
(l)
, and
pairwise diversities (14) are calculated for each
pair of features ( f
(l)
, f
(k)
) from the primary vec-
tor of features (1).
2. For a given n the ensemble F
∗
E
(n) is found as a
solution of the following optimization problem
Q(F
∗
E
(n)|x) = max
F
E
(n)
Q(F
E
(n)|x), (16)
where
Q(F
E
(n)|x) = D(F
E
(n)|x)+
+
1
n
∑
f
(l)
∈F
E
(n)
R( f
(l)
|x). (17)
This step eliminates irrelevant features and keeps
the ensemble of selected features maximally di-
verse.
Then, the ensemble of classifiers
Ψ
∗
= {ψ
l
}, l : f
(l)
∈ F
∗
E
(n) (18)
using selected features is combined by weighted ma-
jority voting on real-value level, where the weights
are equal to the relevance measure (11) of the selected
features. This method leads to the following vector of
class supports produced by the multiclassifier (18) for
given object x ∈ X
d
(DFS)
j
(x) =
∑
l:f
(l)
∈F
∗
E
(n)
R( f
(l)
|x) d
( j)
ψ
l
(x
(l)
) (19)
and final decision is made according to the maximum
rule (2).
2.4 Solution of the Optimization
Problem
The formula (16) presents a combinatorial optimiza-
tion problem, in which we have to choose the best so-
lution from the search space containing 2
L
elements.
As a solution method, we propose to apply genetic al-
gorithm (GA), which is a popular and powerful search
technique. In the conducted experimental investiga-
tions the GA was proceeded as follows:
Coding method – Binary coding was applied for
representation of chromosome. The chromosome is a
string of L binary-valued genes. Value 1 (0) denotes
that a given feature is (is not) a member of an ensem-
ble.
The fitness function – Each chromosome is evalu-
ated using criterion (17).
Initialization – The binary-coded GA starts with
constructing an initial population of individuals, gen-
erated randomly within the search space. Each gene
of the chromosome was a random binary number uni-
formly distributed. The size of population – after the
trials – was set to 2× L.
Selection – In this research a roulette wheel ap-
proach was applied.
Crossover – The crossover process defines how
genes from the parents have been passed to the off-
spring. In experiments a single point crossover was
applied.
Mutation – Mutation is carried out by perturbing
genes of chromosomes after crossover.
The probability of mutation was equal to 0.08.
Stop procedure – Evolution process was termi-
nated after 500 generations.
3 EXPERIMENTS
3.1 Experimental Setup
In order to evaluate the performance of the proposed
feature selection method, the experimental investiga-
tions were made using 9 benchmark data sets taken
from the UCI Machine Learning Repository (Bache
and Lichman, 2013) and Ludmila Kuncheva Collec-
tion (Kuncheva, 2004b) (Laryngeal3). A brief de-
scription of each database is given in Table 1. The
experiments were conducted using MATLAB with
PRTools package (Duin et al., 2007).
Two-fold cross-validation was used to extract
training and testing sets from each data set. For the
calculation of the relevance and diverse measures,
a two-fold stacked generalization method (Wolpert,
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
170

1992) was used. In the method, the training set is
split into two sets A and B of roughly equal sizes. The
set A is first used for the training of the classifiers in
the ensemble, while the set B is used for the calcu-
lation of the relevance and diversity measures. Then,
the set B is used for the training, while the measures
of relevance and diversity are calculated using the set
A. Finally, the measures calculated for both sets are
stacked together and the classifiers in the ensemble
are trained using the union of the sets A and B (i.e.
the original training set). In this way, the measures
of relevance and diversity of features are calculated
for all objects in the original training set, but the data
used for the calculation is unseen during the classifier
training.
Two classifiers were applied in the experiments:
k-NN algorithm for k=3 and Naive Bayes (NB)
method. The performance of the proposed dynamic
feature selection method (DFS) was compared against
the following six state-of-art feature selection meth-
ods with the same 3-NN and NB classifiers:
1. Forward Sequential Wrapper Method (FSw).
In this method at first the best single feature is
chosen, next to the already selected feature we
add another one so as to create the best couple,
then the best three features including the selected
first and second ones are chosen and so one. The
procedure was continued up to n features (Duda
et al., 2012).
2. Backward Sequential Wrapper Method (BSw).
This method is the same as the FSw method, ex-
cept that features are sequentially removed from a
full feature vector until n features is left.
3. Floating Forward Sequential Wrapper
Method (FFSw). This method is the same as the
Fsw method, except that it excludes one feature
at a time from the subset obtained in the previous
step and evaluates the new subset. If excluding a
feature leads to the better result then this feature
is removed, if not, this subset remains unchanged
(Chandrashekar and Sahin, 2014).
4. ReliefF Filter Method (RFf). The ReliefF
method consists of randomly sampling training
objects. For each sampled object its k nearest
neighbors from the same class (called nearest hit)
and from each different class (called nearest miss)
are determined and their contribution is weighted
by the prior distribution of each class. The rel-
evance of feature is computed as the average of
all examples of magnitude of the difference be-
tween the distance to the k nearest hits and the dis-
tance to the k nearest miss, projecting on this fea-
ture. Finally, the features are rankedand those that
exceed a specified threshold are selected (Zafra
et al., 2010).
5. Filter Method Based on Information Gain
(IGf). The information gain of a given feature
with respect to the class number is the reduction
in uncertainty about the class number (class un-
predictability), when we know the value of this
feature (Duda et al., 2012)
6. Filter Ensemble Method (EMf). In the ensem-
ble method the filter feature selectors were ap-
plied. The base feature selectors were based on
the following criteria: Mahalanobis measure, Kol-
mogorov measure, Matusita measure, Informa-
tion gain, ReliefF method, Fisher score (Bolon-
Canedo et al., 2012), (Gu et al., 2012), (Duda
et al., 2012). The feature rankings provided by the
base feature selectors were aggregated into con-
sensus feature ranking by the voting method, i.e.
the sum of feature ranks (Saeys et al., 2008).
Table 1: Datasets used in tests.
Database #Objects #Features #Classes
Ionosphere 351 34 2
Laryngeal3 353 16 3
Wine 178 13 3
Parkinson 197 22 2
Segment. 2310 19 7
Spam 4601 57 2
Dermat. 366 34 6
OptDigits 3823 64 10
PageBlock 5473 10 5
3.2 Results and Discussion
The results obtained for different feature selection
methods using 3-NN and Naive Bayes classifiers are
shown in Tables 2 and 3, respectively. These results
are the classification accuracies (i.e. the percentage
of correctly classified objects) averaged over 10 runs
(5 replications of 2-fold cross validation). Statisti-
cal differences between the performances of the DFS
method and six feature selection methods were eval-
uated using Dietterich 5x2cv test (Dietterich, 1998).
The level of p ≤ 0.05 was considered statistically sig-
nificant. In the Tables, the statistically significant dif-
ferences are marked by asterisks with respect to the
DFS method. In the parenthesis, there are indicated
numbers of features for which the best result for each
method is achieved.
For all feature selection methods, the accuracies
for 3-NN classifier are better than for Naive Bayes
algorithm.
Dynamic Feature Selection with Wrapper Model and Ensemble Approach based on Measures of Local Relevances and Group Diversity
using Genetic Algorithm
171

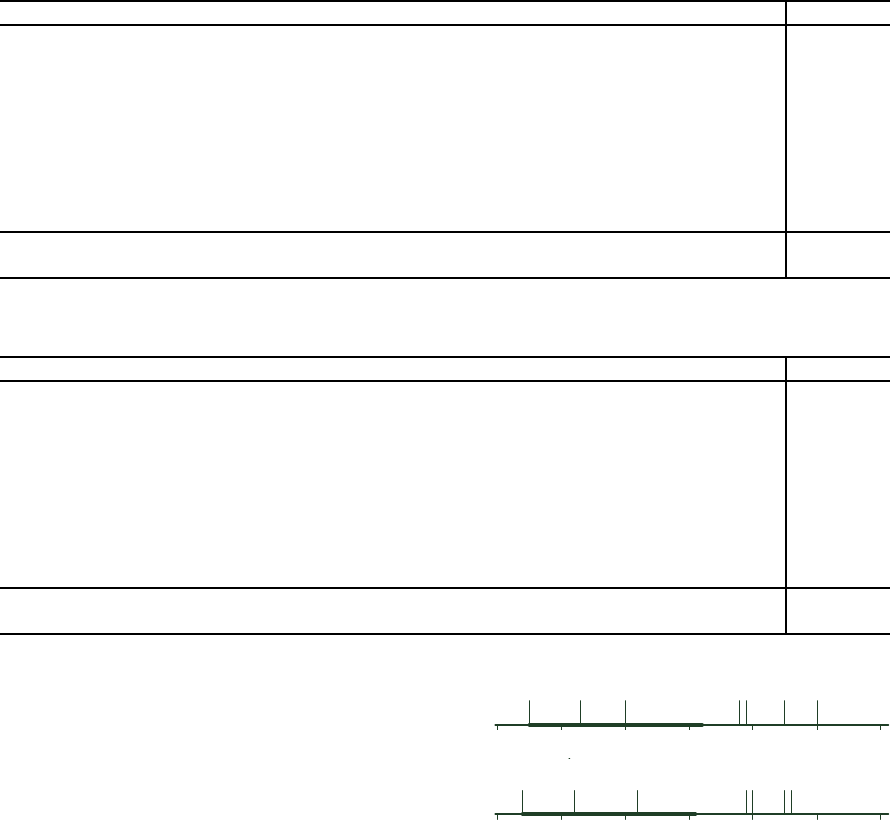
Table 2: Classification accuracies of the feature selection methods for Naive Bayes classifier. The best result for each dataset
is bolded.
Database FSw BSw FFSw RFf GIf EMf DFS
Ionosphere 77.7
∗
(11) 75.5
∗
(13) 79.5(11) 78.8
∗
(13) 80.1(12) 83.4(13) 83.0(10)
Laryngeal3 67.2
∗
(6) 66.9
∗
(7) 66.2
∗
(8) 68.2(7) 67.7
∗
(8) 70.2(9)
71.8(7)
Wine 79.3(8) 77.3
∗
(7) 81.8(6) 84.8(8) 82.6(6) 80.1(6) 83.8(7)
Parkinson 75.3
∗
(9) 76.2
∗
(10) 80.1(11) 78.8(9) 79.3(8) 82.3(8)
83.4(10)
Segmentation 77.2
∗
(8) 77.1
∗
(10) 81.8
∗
(11) 80.5
∗
(11) 78.5
∗
(9) 80.1
∗
(8) 85.2(10)
Spam 73.5
∗
(23) 71.2
∗
(20) 72.2
∗
(22) 79.7(26) 70.4
∗
(21) 78.2(19)
79.1(23)
Dermathology 59.3
∗
(10) 70.1
∗
(12) 73.2
∗
(8) 76.8(13) 74.4
∗
(11) 80.7(13) 79.4(9)
OptDigits 79.8
∗
(26) 80.3
∗
(30) 79.3
∗
(23) 82.9(29) 77.8
∗
(24) 84.9(28)
84.3(26)
Page Block 83.5
∗
(4) 84.1
∗
(7) 81.3
∗
(5) 86.6(7) 82.8
∗
(4) 87.9(5) 89.7(4)
Average rank 5.5 6.0 4.8 3.0 4.9 2.3 1.5
Average 74.7 75.4 77.2 79.6 77.0 80.9 82.8
Table 3: Classification accuracies of the feature selection methods for 3-NN classifier. The best result for each dataset is
bolded.
Database FSw BSw FFSw RFf GIf EMf DFS
Ionosphere 77.2
∗
(10) 79.9(15) 80.6(12) 82.2(13) 81.5(12) 84.5(13) 83.5(12)
Laryngeal3 69.2
∗
(8) 69.7(9) 71.1(10) 70.8(7) 68.8
∗
(8) 73.7(9)
73.0(8)
Wine 78.4
∗
(8) 79.4
∗
(9) 80.5(8) 82.7(8) 84.7(6) 86.3(6) 88.0(9)
Parkinson 77.2
∗
(8) 78.3
∗
(11) 79.3
∗
(10) 80.1(9) 75.5
∗
(8) 82.9(8)
85.2(9)
Segmentation 80.3
∗
(9) 78.1
∗
(11) 81.4
∗
(11) 83.7(11) 86.2(9) 80.2
∗
(8) 85.8(10)
Spam 71.2
∗
(25) 70.1
∗
(21) 67.1
∗
(18) 73.5
∗
(26) 69.9
∗
(21) 75.0(19) 77.6(20)
Dermathology 71.4
∗
(14) 70.9
∗
(12) 74.4(9) 73.9
∗
(13) 73.9
∗
(11) 76.6(13)
77.9(10)
OptDigits 81.1
∗
(28) 81.8
∗
(30) 80.3
∗
(25) 86.1(32) 78.9
∗
(25) 85.9(30) 86.6(27)
Page Block 85.4
∗
(5) 84.9
∗
(7) 83.2
∗
(6) 90.1(7) 84.3
∗
(5) 88.3(6)
89.8(5)
Average rank 5.5 5.6 4.9 3.2 5.0 2.2 1.4
Average 76.8 77.0 77.5 80.3 78.1 81.4 83.0
The DFS method for Naive Bayes classifier out-
performed the FSw, BSw, FFSw, RFf, GIf and EMf
methods by 8.1%, 7.4%, 5.6%, 3.2%, 5.8% and 1.9%,
on average, respectively. The DFS method for 3-NN
classifier outperformed the FSw, BSw, FFSw, RFf,
GIf and EMf methods by 6.2%, 6.0%, 5.5%, 2.7%,
4.9% and 1.6%, on average, respectively.
The method developed produced statistically sig-
nificant higher accuracies, than the other feature se-
lection methods, in 62 out of 108 cases (9 datasets ×
6 feature selection methods compared × 2 classifier
types used).
Statistical differences in rank between the FS
methods were obtained using a Friedman test with
Iman and Davenport correction combined with a post
hoc Holm stepdown procedure (Demˇsar, 2006). The
average ranks of the FS methods and a critical rank
difference, calculated using a Bonferroni – Dunn test
(Demˇsar, 2006), are visualised in Fig. 1. The level of
p < 0.05 was considered as statistically significant.
The DFS method has statistically higher average rank
than all feature selection methods but EMf and RFf
methods.
3
4
5 6 7
EMf
DFS
FSw
IGf
BSw
FFSw
21
3
4
5 6 7
EMfDFS
FSw
IGf BSwFFSwRFf
21
A)
B)
RFf
Figure 1: Average ranks of the feature selection methods
for different classifiers: A) Naive Bayes classifier, B) 3-
NN classifier. Thick interval is the critical rank differ-
ence (2.686) calculated using the Bonferroni – Dunn test
(p < 0.05).
4 CONCLUSIONS
Feature selection is the process of detecting the rel-
evant features and discarding the irrelevant ones. A
correct selection of the features leads to the im-
provement of classifier learning procedure in terms of
learning speed, generalization capacity and simplicity
of the induced model (Bolon-Canedo et al., 2012).
In this work, the novel ensemble feature selec-
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
172

tion method using wrapper model is proposed. In the
method, the features are selected in dynamic mode,
i.e. the set of selected features can be different for dif-
ferent test objects in contrast to the static mode, where
the selected set of features is the same for all test ob-
jects. In the selection procedure, we formulate the
optimal feature selection problem adopting the sum
of relevance of features and diversity of feature en-
semble as an optimality criterion. Since this problem
can not be directly solved using analytical ways, we
propose to apply genetic algorithm (GA).
The performance of proposed feature selection
method (DFS) was experimentally verified using 7
real benchmark data sets. The DFS method out-
performed the six state-of-art feature selection algo-
rithms in terms of the quality of the feature subset and
the classification accuracy.
There are some avenues for future research. First,
we can consider the cost associated with each fea-
ture, which in the optimization problem (16) can play
the role of constraints. It means, that feature selec-
tion method should maximize the sum of relevance
of features and diversity of feature ensemble in dy-
namic fashion, and simultaneously should keep the
cost of measure of member features on an acceptable
level. Second, we can apply for solving optimization
problem (16) other heuristic optimization procedures,
e.g. the simulated annealing (SA) algorithm. As it
results from the authors’ earlier experience (Lysiak
et al., 2014), the SA method is faster than the GA
algorithm, which can have great practical importance.
ACKNOWLEDGEMENTS
We would like to thank the anonymous reviewers for
their constructive comments and helpful suggestions.
This work was financed from the National Science
Center resources in 2012-2014 as a research project
No ST6/06168 and supported by the statutory funds
of the Department of Systems and Computer Net-
works, Wroclaw University of Technology.
REFERENCES
Bache, K. and Lichman, M. (2013). UCI machine learning
repository.
Bolon-Canedo, V., Sanchez-Marono, N., and Alonzo-
Betandos, A. (2012). A review of feature selection
methods on synthetic data. Knowledge Information
System, 34:483–519.
Chandrashekar, G. and Sahin, F. (2014). A survey on fea-
ture selection methods. Computers and Electrical En-
gineering, 40:16–28.
Demˇsar, J. (2006). Statistical comparisons of classifiers
over multiple data sets. The Journal of Machine
Learning Research, 7:1–30.
Dietterich, T. (1998). Approximate statistical tests for com-
paring supervised classification learning algorithms.
Neural Computation, 10:1895–1923.
Duda, R., Hart, P., and Stork, D. (2012). Pattern Classifica-
tion. Wiley Interscience, New York.
Duin, R., Juszczak, P., Pekalska, E., and et al. (2007). A
matlab toolbox for pattern recognition.
Goldberg, D. (1989). Genetic Algorithms in Search, Op-
timization and Machine learning. Addison-Wesley
Publishing Company, London.
Gu, Q., Li, Z., and Han, J. (2012). Generalized fisher score
for feature selection. CoRR, abs/1202.3725.
Guyon, I. and Elisseeff, A. (2003). An introduction to vari-
able and feature selection. Journal on Machine Learn-
ing Research, 3:1157–1182.
Kuncheva, L. (2004a). Combining Pattern Classifier: Meth-
ods and Algorithms. Wiley-Interscience, London.
Kuncheva, L. (2004b). Ludmila kuncheva collection.
Lysiak, R., Kurzynski, M., and Woloszynski, T. (2014). Op-
timal selection of ensemble classifiers using measures
of competence and diversity of base classifiers. Neu-
rocomputing, 126:29–35.
Saeys, Y., Abeel, T., and Van de Peer, Y. (2008). Ro-
bust feature selection using ensemble feature selec-
tion techiques. Lecture Notes in Artificial Intelligence,
5212:313–325.
Saeys, Y., Inza, I., and Larranaga, P. (2007). A review of
feature selection techniques in bioinformatics. Bioin-
formatics, 23:2507–2517.
Wang, H., Khoshgoftaar, T., and Napolitano, A. (2010).
A comparative study of ensemble feature selection
techniques for software defect prediction. In 2010
Ninth Int. Conf. on Machine Learning and Applica-
tions, pages 135–140. IEEE Computer Society.
Woloszynski, T. (2013). Classifier competence based on
probabilistic modeling (ccprmod.m) at matlab central
file exchange.
Woloszynski, T. and Kurzynski, M. (2010). A measure
of competence based on randomized reference classi-
fier for dynamic ensemble selection. In 2010 Twenti-
eth International Conference on Pattern Recognition,,
pages 4194–4197. Int. Association on Pattern Recog-
nition.
Woloszynski, T. and Kurzynski, M. (2011). A probabilistic
model of classifier competence for dynamic ensemble
selection. Pattern Recognition, 44(10-11):2656–2668.
Woloszynski, T., Kurzynski, M., Podsiadlo, P., and Sta-
chowiak, G. (2012). A measure of competence based
on random classification for dynamic ensemble selec-
tion. Information Fusion, 13:207–213.
Wolpert, D. H. (1992). Stacked generalization. Neural Net-
works, 5:214–259.
Zafra, A., Pechenizkiy, M., and Ventura, S. (2010). Reduc-
ing dimensionality in multiple instance learning with
a filter method. Lecture Notes in Computer Science,
6077:35–44.
Dynamic Feature Selection with Wrapper Model and Ensemble Approach based on Measures of Local Relevances and Group Diversity
using Genetic Algorithm
173