A Reward-driven Model of Darwinian Fitness

Jan Teichmann

, Eduardo Alonso

and Mark Broom

Department of Mathematics, City University London, London EC1V 0HB, U.K.

Department of Computer Science, City University London, London EC1V 0HB, U.K.

Keywords: Darwinian Fitness, Reward, Prey-predator Co-evolution.

Abstract: In this paper we present a model that, based on the principle of total energy balance (similar to energy

conservation in Physics), bridges the gap between Darwinian fitness theories and reward-driven theories of

behaviour. Results show that it is possible to accommodate the reward maximization principle underlying

modern approaches in behavioural reinforcement learning and traditional fitness approaches. Our

framework, presented within a prey-predator model, may have important consequences in the study of

behaviour.

1 INTRODUCTION

In an evolutionary context, models such as optimal

foraging theory (OFT) look at behaviour from the

point of view of maximizing Darwinian fitness (e.g.,

Orr, 2009). On the other hand, the fact that animals

show clear reward driven motivations has been

extensively reported (Barto et al., 1990; Sutton and

Barto, 1998). From the evolutionary perspective

models assume a monotonically increasing

functional relationship between rewards and fitness.

In such a scenario optimization of rewards seems

like a straightforward choice. Nevertheless, the

success of reward mediated learning as an

omnipresent adaptation to the environment can

easily deceive the observer into believing that this

assumption, that animals just optimize rewards, is

generally true (Staddon, 2007), and, very little is still

known about the relationship between behavioural

and genetic traits. To fully understand the evolution

of animal behaviour we require both mechanistic

and functional approaches. The mechanistic

approach tries to quantify the influence of genetic

and environmental factors on the phenotype,

whereas the functional approach tries to describe

how the interaction of phenotypes and their

environment affects fitness. Functional approaches

towards understanding behaviour have received very

little attention (see, for example, Dingemanse and

Réale, 2005). Similarly, it is evident that,

notwithstanding the accomplishments of

computational theories of reinforcement learning in

modelling neural and psychological factors (e.g.,

Dayan and Daw, 2008; Rangel et al., 2008; Schultz,

2008), the use of rewards in this area is a great

simplification of the true nature of rewards

(Teichmann et al., 2014). Although new ways to

enrich the reinforcement learning ontology with

ethological and evolutionary information have been

reported (Alonso et al., 2015), the problem of

integrating reward-driven approaches and fitness

theories has not been tackled so far. It is apparent

that whereas rewards reflect some fitness

component, a general relationship between strength

of rewards and fitness needs to be established.

The question is: is it possible to determine the

fitness component of rewards from the

environmental set-up and the behaviour of

predators? In order to solve this conundrum we have

assumed that predators generally show evolved

behaviour adapted to their environment and that

without the occurrence of new mutants selection is

of a stabilizing nature: the end-result is a stable

system of balanced interactions of co-evolved

predators and all their prey. We use the stability

argument to infer the fitness components of

subjective rewards. The observed environment is

interpreted as an evolutionarily stable snapshot

without the presence of any mutants with fitness

advantages/disadvantages. The resulting model has

been used previously to model the outcome of

reward driven learning (Teichmann, 2014) and the

aim of this paper is to compare the results of reward

driven learned behaviour with the prediction of the

174

Teichmann, J., Alonso, E. and Broom, M..

A Reward-driven Model of Darwinian Fitness.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 174-179

ISBN: 978-989-758-157-1

fitness component of this model assuming energy

balance and evolutionary stability.

2 THE PREDATOR LIFETIME

MODEL

This section introduces the lifetime model of an

individual predator and the definition of the

individual’s fitness based on its interaction with the

environment in the form of payoffs and additional

aspects of its behaviour, metabolism, and lifetime

traits, age specifically.

We model a situation where the predator faces

different types of prey. These are either aposematic,

which are prey with invisible defences (such as

toxins) advertised by a clear signal (such as bright

colouration), or Batesian mimics, which are

undefended. We shall simply refer to the former type

as “models” and the latter as “mimics”. The predator

feeds on prey it encounters, as it cannot distinguish

between models and mimics based on their

appearance. However, the predator has the option to

move around freely in its environment to avoid

encounters with possibly aversive defended prey

based on its experience. Under the assumption of

interim stability without the presence of mutants it

follows that

 Eu



 R 0,

(1)

with

representing the metabolic cost of the

predator as time

passes during interaction

with

the prey,



the behavioural expenditure (an

energy related quantity defined as the energetic cost

of behaviour including, amongst others, locomotion

and reproduction), and

being the influx of some

fitness quantity from predation. These terms can be

interpreted as a form of energy and, generally,

 0

and

R 0

. If this condition is not met,

and the l.h.s. in Eq (1) is positive, the population of

predators would grow; and if the l.h.s. is negative,

the population of predators would shrink. In a

coupled system of co-evolution this would lead to

changing selective pressure on the prey population,

which is assumed to be stabilizing. For simplicity we

assume that the system has reached a stable point of

balanced interactions between predator and prey.

It must we noted that co-evolutionary dynamical

systems, in particular with multiple prey species, can

have many possible solutions, including cycling and

species extinction as well as a unique equilibrium.

We have focused only on the fitness of the predator,

through Eq. (1), and have not given the equivalent

functions for the different prey species at all. These

could take a wide number of forms. We don’t mean

to imply that under any given prey fitness function

there would be a stable equilibrium; only that there

would be a range of plausible scenarios which would

yield a stable equilibrium, and that we concentrate

on these cases only. In particular, an extreme case

would be if the fitness of the prey does not greatly

depend upon the fitness of our predator (they may

have many predators, others of which are more

numerous, or their mortality will be driven by

internal competition), when the system approximates

to a single species system given by Eq. (1). The

results in the next section will hold for all cases

which yield an equilibrium, but also for cycles of

sufficiently small amplitude. Of course, there can be

systems with species persistence and significant

oscillations where our results do not hold.

The total available prey from the prey population

is given by,

 g

X,Y





dxdy  2p



i ,x



i ,y



(2)

where



is a normalization factor and the dispersion

of each prey population

within the environment is

described by a Gaussian function

X,Y







exp 

X  x

i ,0





i ,x



Y  y

i ,0





i ,y

























(3)

with

i ,0

, y

i,0





being the centre of the prey

population with density

, and



i ,x



i ,y



the

spread of the prey. The payoff, aka the reward, is

defined as

R G





r * t





(4)

with

r *

being the assumed fitness component of the

payoff,

the cost incurred by ingesting toxins, and





the probability of ingesting a prey individual

of toxicity

after taste sampling as given by





1 d

(5)

We assume that

r *

is related to the fitness of the

prey. For example, if fitness is measured in terms of

energy the predator has a high fitness influx from a

prey which also had a great amount of energy

A Reward-driven Model of Darwinian Fitness

175

reserves for reproduction. Moreover, if

r *

relates to

the fitness of the prey this value has to be equal for

different types of prey under the assumption of

stability. If the fitness contribution of a type of prey

would be greater than the fitness of other prey types

it would be advantageous for the predator to feed

exclusively on this prey. It is apparent that fitness in

such an interpretation is not equivalent to the

standard idea of fitness of the number of offspring

surviving to reproductive age. Here

r *

is better

interpreted as an energetic quantity from which

individuals can allocate towards the cost of predator

defences, reproduction, metabolic costs of toxin

ingestion, or behavioural expenditures.

In summary, the fitness component

r *

for a

predator prey interaction with just a single type of

prey is given by

r* 





 t



 dt





 t















(6)

Eq. (6) consists of a scaling factor and the sum of

the predator's behavioural expenditure, its basal

metabolic cost, and the additional costs of foraging

such as the sampling of prey

, the handling of prey

, and the recovery from ingested toxins







represents the age dependent agility of the predator,

given by









(7)

In short, we solve Eq. (1) for

r *

by substituting for

with the definition in Eq. (6). Consequently,

r *

needs to be higher when (i) a predator feeds on toxic

prey; (ii) when the prey requires lengthy handling;

(iii) prey is rare; (iv) the predator has a high

metabolic rate

; (v) the predator utilizes costly

behaviour; or (vi) when predators live longer. On the

predator’s side

r *

can be termed the nutritional

value of prey within this context.

If we consider a predator feeding on an

aposematic prey in the presence of a Batesian mimic

the lifetime model needs to be refined to

accommodate the fact that the predator cannot

distinguish between the two prey populations and

has to use experience obtained from previous

exploration. As such both prey populations

experience some levels of predation. Moving to

multiple food sources

under the assumption of

stability gives the following condition

0  R

 t

 Eu





(8)

As discussed, we assume that both types of prey

contribute the same value of

r *

whereas the models

allocate parts of their energy inventory towards the

cost of their anti-predator defences and mimics have

to allocate greater amounts towards reproduction to

compensate for higher levels of predation, especially

in the case of predators which are able to taste-

sample their prey. Consequently,

r *

in the model-

mimic system is given as follows:

r* 









 t

 G

 d







t,i

 t

h,i









































(9)

That is, the case of multiple prey types is a direct

extension of the case of a single prey type in Eq. (6)

where the scaling factor and the outcome of

interaction with the prey is the sum over all the

contributing prey types.

3 RESULTS

The results in Figure 1 show the effects of different

aspects of the lifetime model on the nutritional value

r *

in the context of a single prey type. We see that

increasing prey abundance



reduces the required

nutritional value of prey. Nevertheless, there is a

minimal nutritional value prey must have which

depends on the metabolic rate of the predator

and

which is independent of the predator’s behavioural

expenditure





and the prey’s abundance



(Figures 1a and 1b). If prey is rare, the predator’s

behavioural expenditure



has a much greater

impact on

r *

than its metabolic rate

. The age

distribution or longevity of predators acts as a

simple multiplicative factor in this context. Figures

1(c) and 1(d) show the effects of prey toxicity t on

the nutritional requirement

r *

. Generally,

increasing prey toxicity t requires higher nutritional

values

r *

for stability. In the case of less toxic prey

the predator’s behavioural expenditure



again

has a greater impact on

r *

than its metabolic rate.

With increasing prey toxicity the predator’s

metabolic rate has greater impact on

r *

. The age

distribution or longevity of predators acts not just as

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

176

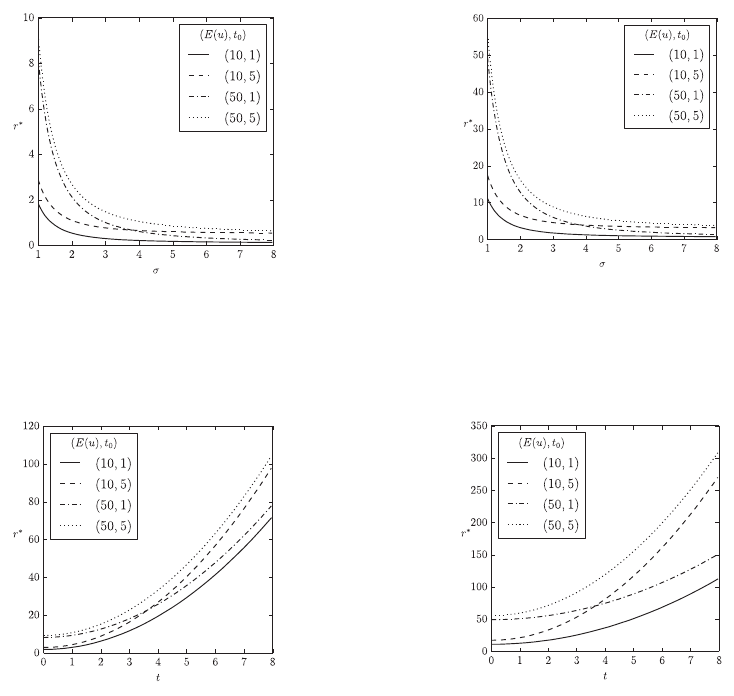
(a) The fitness component

r *

of a single prey type with respect

to the prey population’s abundance



, the predator’s behavioural

costs



, and the predator’s metabolic rate

. Hence there is

no ageing, i.e.,



A  0



 1

(b) The same as 1(a) with age distribution given by



r *

of a single prey type with respect

to the prey population’s toxicity t, the predator’s behavioural costs



, and the predator’s metabolic rate

. Here we have



 1

, and no ageing,



A  0



 1

(d) The same as 1(c) with age distribution given by

A  5

Figure 1: Effects of a single aposematic prey population on the fitness component

r *

in a stable predator-prey

environment without taste sampling:



 1



0.1

, and



0.1

a simple factor relating to prey toxicity, as it was the

case in prey abundance.

Figure 2 shows the results of Eq. (9) on the

dependency of different parameters of the model.

The overall prey abundance is held constant in all

charts. Figures 2(a) and 2(b) show the effects of a

second aposematic type of prey in comparison to an

environment with only one aposematic prey type. In

the case that the second aposematic prey is less

(more) toxic than the first prey type it reduces

(increases)

r *

overall. An increasing fraction of the

second prey type amplifies the effects on

r *

Additionally, taste sampling also amplifies the effect

of the second prey type on

r *

. However, the impact

of taste sampling is greater if the second prey type is

less toxic than the first prey type. Figures 2(c) and

2(d) show the effects of mimics. Generally, the

presence of mimics lowers

r *

and mimics have an

increasing impact on

r *

with increasing toxicity of

the aposematic model

. In the case of non-taste-

sampling predators the effect of mimics on

r *

linear with respect to the fraction of mimics in the

overall prey population

Taste-sampling generally

increases

r *

and the effect of mimics on

r *

becomes non-linear with increasing impact in the

case of mimics being rare.

A Reward-driven Model of Darwinian Fitness

177

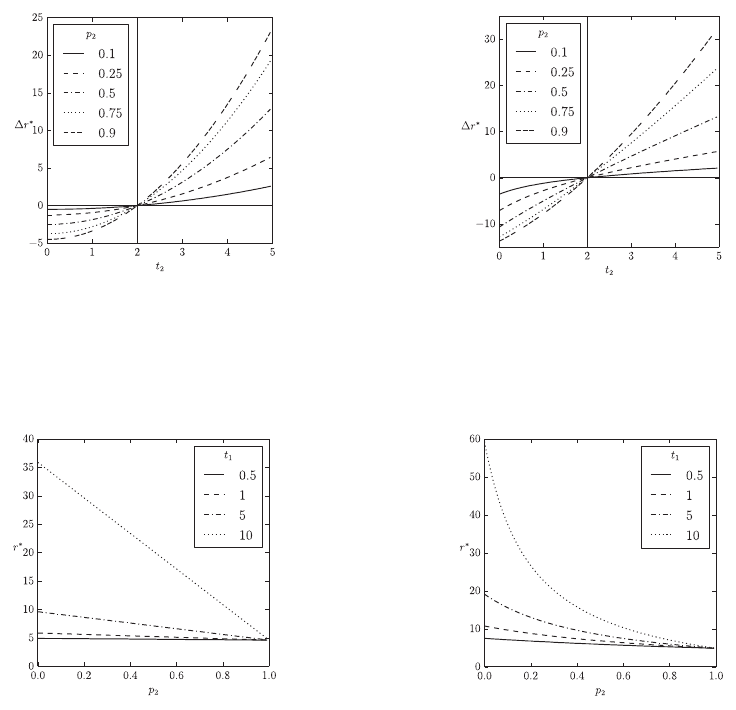
(a) Effects of a second aposematic prey population with respect to

its level of defence

and density

. The horizontal line

r*  0

and the vertical line

 2

indicate no differences.

Here there is no taste sampling



 1

, with



and

 1 p

(b) The same as 2(a) but with taste sampling with

 1

, and



0.1



, and





with respect to the mimics density

and the models toxicity

. Here there is no taste sampling



 1,

and



 1 p

(d) The same as 2(c) but with taste sampling with

 1,

and



0.1





Figure 2: Effects of aposematic prey expressed as the relative change in the fitness component

r *

in a stable predator-

prey environment with multiple prey populations when compared to an environment with a single prey-population. Here

 0.1

 0.25



 25



A  0



 1

, and





. The total prey abundance



is held constant.

4 CONCLUSIONS

In this paper we have presented a predator lifetime

model including traits such as metabolic costs,

locomotion, prey handling, and toxin recovery,

which had been abstracted away in the previous

studies of behaviour. The fitness quantity is obtained

by assuming a stabilizing co-evolution between

predator and prey and can be interpreted as a form of

energy. On the predator’s side this might be the

nutritional value of prey and on the prey’s side it

might be interpreted as an energy inventory which

the prey can allocate towards the costs of defence

and reproduction. Aposematic prey allocate a greater

amount towards the cost of its defence whereas the

mimics have to allocate a greater amount towards

their reproduction due to higher predation risks from

experienced predators. The presence of mimics

generally lowers the value of

r *

needed for such a

system to be stable. If models and mimics co-exist

with an unchanged

r *

we predict that the models

will be better defended than in the corresponding

scenarios without mimics.

If mimics and models co-exist but with

unchanged levels of defence then models are

predicted to be smaller and have lower nutritional

value than in a system without mimics. Taste-

sampling as a strategy increases

r *

if mimics are

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

178

rare or if models are only moderately well defended.

However, the impact of taste sampling is non-linear

especially in systems with highly defended models.

In such situations taste-sampling lowers

r *

Consequently, under the assumption of a fixed value

for

r *

and stability, a predator evolves a taste-

sampling strategy because mimics are less common

or models are better defended than in a comparable

stable environment where predators do not utilize

taste sampling.

Another interesting aspect is the effect of

different age distributions: in general longevity in

predators increases

r *

. The effects are linear with

regards to prey abundance but non-linear with

regards to prey toxicity where behavioural

expenditure gains increasing impact in the case of

defended prey and older predators, whereas

metabolic costs have an increased impact in the case

of non-defended prey. The main conclusions of this

paper are as follows:

 On the predator’s side

r *

is related to the

nutritional value of prey and on the prey’s side

it relates to an energy inventory which can be

allocated, amongst other things, towards the

cost of defences or reproduction;

 Behavioural expenditure has a greater impact

than metabolic costs when prey is rare and

undefended;

 Metabolic costs have a greater impact when

prey is abundant or highly defended;

 Longevity of the predator increases the

importance of behavioural expenditure in the

case of highly defended prey and the impact of

metabolic costs if prey is undefended;

 Mimics generally lower

r *

which leads to less

nutritional prey or better defended models if

r *

is meant to be unchanged;

 Predators utilize taste sampling if mimics are

rare or models are highly toxic.

REFERENCES

Alonso, E., Fairbank, M., and Mondragón, E. (2015).

Back to optimality: A formal framework to express the

dynamics of learning optimal behavior. Adaptive

Behavior, 23(4), 206-215.

Barto, A.G., Sutton, R.S., and Watkins, C.J.C.H. (1990).

Learning and sequential decision making. In Learning

and Computational Neuroscience: Foundations of

Adaptive Networks, M. Gabriel and J.W. Moore, Eds.,

pp. 539-602, Cambridge, Mass: MIT Press.

Dayan, P., and Daw, N.D. (2008). Decision theory,

reinforcement learning, and the brain, Cognitive,

Affective, & Behavioral Neuroscience 8, 429–453.

Dingemanse, N. J., and Réale, D. (2005). Natural selection

and animal personality, Behavior 142, 1159–1184.

Orr, H. A., (2009). Fitness and its role in evolutionary

genetics. Nature Review Genetics 10, 531-539.

Rangel, A., Camerer, C., and Montague, P.R. (2008). A

framework for studying the neurobiology of value-

based decision making, Nature Reviews Neuroscience

9, 545–556.

Schultz, W. (2008). Neuroeconomics: the promise and the

profit, Philosophical Transactions of the Royal Society

B: Biological Sciences 363, 3767–3769.

Staddon, J.E. (2007). Is animal behavior optimal? In A.

Bejan & G.W. Merkx (eds.) Constructal Theory of

Social Dynamics, NY: Springer.

Sutton, R.S., and Barto, A.G. (1998). Reinforcement

learning: An introduction, Boston, MA: Cambridge

University Press.

Teichmann, J. (2014). Models of aposematism and the role

of aversive learning. PhD dissertation, City University

London, London, UK.

Teichmann, J., Broom, M., and Alonso, E. (2014). The

application of temporal difference learning in optimal

diet models, Journal of Theoretical Biology 340, 11–

16.

A Reward-driven Model of Darwinian Fitness

179