Multi-Strategy Genetic Algorithm for Multimodal Optimization

Evgenii Sopov

Department of Systems Analysis and Operations Research, Siberian State Aerospace University, Krasnoyarsk, Russia

Keywords: Multimodal Optimization, Self-Configuration, Genetic Algorithm, Metaheuristic, Niching.

Abstract: Multimodal optimization (MMO) is the problem of finding many or all global and local optima. In recent

years many efficient nature-inspired techniques (based on ES, PSO, DE and others) have been proposed for

real-valued problems. Many real-world problems contain variables of many different types, including

integer, rank, binary and others. In this case, the weakest representation (namely binary representation) is

used. Unfortunately, there is a lack of efficient approaches for problems with binary representation. Existing

techniques are usually based on general ideas of niching. Moreover, there exists the problem of choosing a

suitable algorithm and fine tuning it for a certain problem. In this study, a novel approach based on a

metaheuristic for designing multi-strategy genetic algorithm is proposed. The approach controls the

interactions of many search techniques (different genetic algorithms for MMO) and leads to the self-

configuring solving of problems with a priori unknown structure. The results of numerical experiments for

classical benchmark problems and benchmark problems from the CEC competition on MMO are presented.

The proposed approach has demonstrated efficiency better than standard niching techniques and comparable

to advanced algorithms. The main feature of the approach is that it does not require the participation of the

human-expert, because it operates in an automated, self-configuring way.

1 INTRODUCTION

Many real-world problems have more than one

optimal solution, or there exists only one global

optimum and several local optima in the feasible

solution space. Such problems are called

multimodal. The goal of multimodal optimization

(MMO) is to find all optima (global and local) or a

representative subset of all optima.

Evolutionary and genetic algorithms (EAs and

GAs) demonstrate good performance for many

complex optimization problems. EAs and GAs are

also efficient in the multimodal environment as they

use a stochastic population-based search instead of

the individual search in conventional algorithms. At

the same time, traditional EAs and GAs have a

tendency to converge to the best-found optimum

losing population diversity.

In recent years MMO have become more

popular, and many efficient nature-inspired MMO

techniques were proposed. Almost all search

algorithms are based on maintaining the population

diversity, but differ in how the search space is

explored and how optima basins are located and

identified over a landscape. The majority of

algorithms and the best results are obtained for real-

valued MMO problems (Das et al., 2011). The main

reason is the better understanding of landscape

features in the continuous search space. Thus many

well-founded heuristics can be developed.

Unfortunately many real-world MMO problems

are usually considered as black-box optimization

problems and are still a challenge for MMO

techniques. Moreover, many real-world problems

contain variables of many different types, including

integer, rank, binary and others. In this case, usually

binary representation is used. Unfortunately, there is

a lack of efficient approaches for problems with

binary representation. Existing techniques are

usually based on general ideas of niching and fitness

sharing. Heuristics from efficient real-valued MMO

techniques cannot be directly applied to binary

MMO algorithms because of dissimilar landscape

features in the binary search space.

In this study, a novel approach based on a

metaheuristic for designing multi-strategy MMO GA

is proposed. Its main idea is to create an ensemble of

many MMO techniques and adaptively control their

interactions. Such an approach would lead to the

self-configuring solving of problems with a priori

unknown structure.

The rest of the paper is organized as follows.

Section 2 describes related work. Section 3 describes

Sopov, E..

Multi-Strategy Genetic Algorithm for Multimodal Optimization.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 55-63

ISBN: 978-989-758-157-1

the proposed approach. In Section 4 the results of

numerical experiments are discussed. In the

Conclusion the results and further research are

discussed.

2 RELATED WORK

The problem of MMO has exists since the first EAs.

The first MMO techniques were applied in EAs and

GAs for improvement in finding the global optimum

in the multimodal environment.

The MMO, in general, can have at least 3 goals

(Preuss, 2014):

 to find a single global optimum over the

multimodal landscape only;

 to find all global optima;

 to find all optima (global and local) or a

representative subset of all optima.

It is obvious that the second and the third goals

are more interesting from both a theoretical and a

practical point of view.

Over the past decade interest for this field has

increased. The recent approaches are focused on the

goal of exploring the search space and finding many

optima to the problem. Many efficient algorithms

have been proposed. In 2013, the global completion

on MMO was held within IEEE CEC'13 (Li et al.,

2013a).

The list of widespread MMO techniques includes

(Das et al., 2011; Liu et al., 2011; Deb and Saha,

2010):

1. General techniques:

 Niching (parallel or sequential)

 Fitness sharing, Clearing and Cluster-based

niching

 Crowding and Deterministic crowding

 Restricted tournament selection (RTS)

 Mating restriction

 Species conservation

2. Special techniques:

 Niching memetic algorithm

 Multinational EA

 Bi-objective MMO EA

 Clustering-based MMO EA

 Population-based niching

 Topological algorithms

3. Other nature-inspired techniques:

 PSO, ES, DE, Ant Colony Optimization and

others

Binary and binarized MMO problems are usually

solved using the GA based on general techniques.

Also special techniques are applied, but some of

their features can be lost in the binary space.

Unfortunately, many efficient nature-inspired MMO

algorithms have no binary version and cannot be

easily converted to binary representation.

As we can see from many studies, there is no

universal approach that is efficient for all MMO

problems. Many researches design hybrid

algorithms, which are generally based on a

combination of search algorithms and some heuristic

for niching improvement. For example, here are four

top-ranked algorithms from the CEC’13 competition

on MMO: Niching the CMA-ES via Nearest-Better

Clustering (NEA2), A Dynamic Archive Niching

Differential Evolution algorithm (dADE/nrand/1),

CMA-ES with simple archive (CMA-ES) and

Niching Variable Mesh Optimization algorithm (N-

VMO) (Li et al., 2013b).

Another way is combining many basic MMO

algorithms to run in parallel, migrate individuals and

combine the results. In (Bessaou et al., 2000) an

island model is applied, where islands are iteratively

revised according to the genetic likeness of

individuals. In (Yu and Suganthan, 2010) four MMO

niching algorithms run in parallel to produce

offspring, which are collected in a pool to produce a

replacement step. In (Qu et al., 2012) the same

scheme is realized using the clearing procedure.

The conception of designing MMO algorithms in

the form of an ensemble seems to be perspective. A

metaheuristic that includes many different MMO

approaches (different search strategies) can deal

with many different MMO problems. And such a

metaheuristic can be self-configuring due to the

adaptive control of the interaction of single

algorithms during the problem solving.

In (Sopov, 2015) a self-configuring multi-

strategy genetic algorithm in the form of a hybrid of

the island model, competitive and cooperative

coevolution was proposed. The approach is based on

a parallel and independent run of many versions of

the GA with many search strategies, which can deal

with many different features of optimization

problems inside the certain optimization class. The

approach has demonstrated good results with respect

to multi-objective and non-stationary optimization.

3 MULTI-STRATEGY MMO GA

In the field of statistics and machine learning,

ensemble methods are used to improve decision

making. On average, the collective solution of

multiple algorithms provides better performance

than could be obtained from any of the constituent

algorithms. This concept can be also used in the

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

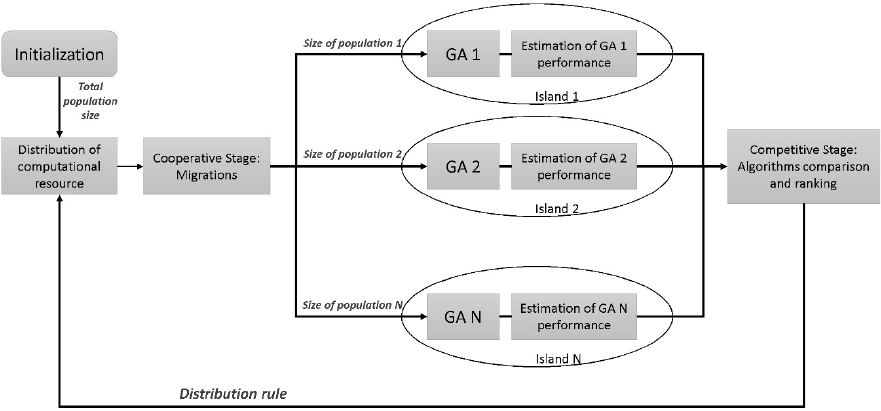
Figure 1: The Self*GA structure.

field of EA. The main idea is to include different

search strategies in the ensemble and to design

effective control of algorithm interaction. Our

hypothesis is that different EAs are able to deal with

different features of the optimization problem, and

the probability of all algorithms failing with the

same challenge in the optimization process is low.

Moreover, the interaction of algorithms can provide

the ensemble with new options for optimization,

which are absent in stand-alone algorithms.

The general structure of the self-configuring

multi-strategy genetic algorithm proposed in (Sopov,

2015) is called Self*GA (the star sign corresponds to

the certain optimization problem) and it is presented

in Figure 1.

The total population size (or the sum of

populations of all stand-alone algorithms) is called

the computational resource. The resource is

distributed between algorithms, which run in parallel

and independent over the predefined number of

iterations (called the adaptation period). All

algorithms have the same objective and use the same

encoding (solution representation). All populations

are initialized at random. After the distribution, each

GA included in Self*GA has its own population

which does not overlap with populations of other

GAs. At the first iteration, all algorithms get an

equal portion of the resource. This concept

corresponds to the island model, where each island

realizes its own search strategy.After the adaptation

period, the performance of individual algorithms is

estimated with respect to the objective of the

optimization problem. After that algorithms are

compared and ranked. Search strategies with better

performance increase their computational resource

(the size of their populations). At the same time, all

algorithms have a predefined amount of resource

that is not distributed to give a chance for algorithms

with low performance. This concept corresponds to

the competitive coevolution scheme.

Finally, migrations of the best solutions are set to

equate the start positions of algorithms for the run

with the next adaptation period. According to the

optimization problem, such a migration can be

deterministic, selection-based or random. This

concept corresponds to cooperative coevolution.

Such a technique eliminates the necessity to

define an appropriate search strategy for the problem

as the choice of the best algorithm is performed

automatically and adaptively during the run.

Now we will discuss the design of a Self*GA for

MMO problems that can be named SelfMMOGA.

At the first step, we need to define the set of

individual algorithms included in the SelfMMOGA.

In this study we use six basic techniques, which are

well-studied and discussed (Singh and Deb, 2006;

Das et al., 2011), and they can be used with binary

representation with no modification. Algorithms and

their specific parameters are presented in Table 1.

All values for radiuses and distances in Table 1 are

in the Hamming metric for binary problems and in

the Euclidean metric for continuous problems.

The motivation of choosing certain algorithms is

that if the SelfMMOGA performs well with basic

techniques, we can develop the approach with more

complex algorithms in further works.

The adaptation period is a parameter of the

SelfMMOGA. Moreover, the value depends on the

Multi-Strategy Genetic Algorithm for Multimodal Optimization

Table 1: Algorithms include in the SelfMMOGA.

Algorithm Parameters

Alg1 Clearing

Clearing radius, Capacity of

a niche

Alg2 Sharing

Niche radius, α

Alg3 Clustering

Number of clusters, min

distance to centroid, max

distance to centroid

Alg4

Restricted

Tournament

Selection (RTS)

Window size

Alg5

Deterministic

Crowding

Alg6

Probabilistic

Crowding

limitation of the computational resource (total

number of fitness evaluations).

The key point of any coevolutionary scheme is

the performance evaluation of a single algorithm.

For MMO problems performance metrics should

estimate how many optima were found and how the

population is distributed over the search space.

Unfortunately, good performance measures exist

only for benchmark MMO problems, which contain

knowledge of the optima. Performance measures for

black-box MMO problems are still being discussed.

Some good recommendations can be found in

(Preuss and Wessing, 2013). In this study, the

following criteria are used.

The first measure is called Basin Ratio (BR). The

BR calculates the number of covered basins, which

have been discovered by the population. It does not

require knowledge of optima, but an approximation

of basins is used. The BR can be calculated as













(1)

=1,,





∈















,



=

1,∈

0,

where pop is the population, k is the number of

identified basins by the total population, l is the

indicator of basin coverage by a single algorithm, b

is a function that indicates if an individual is in basin

To use the metric (1), we need to define how to

identify basins in the search space and how to

construct the function b(x,z).

For continuous MMO problems, basins can be

identified using different clustering procedures like

Jarvis-Patrick, the nearest-best and others (Preuss et

al., 2011). In this study, for MMO problems with

binary representation we use the following approach.

We use the total population (the union of

populations of all individual algorithms in the

SelfMMOGA). For each solution, we consider a

predefined number of its nearest neighbours (with

respect to the Hamming distance). If the fitness of

the solution is better, it is denoted as a local optima

and the centre of the basin. The number of

neighbours is a tunable parameter. For a real-world

problem, it can be set from some practical point of

view. The simplified basin identification procedure

is described using a pseudo-code as follows:

Z=∅;

for all (x ∈ total population)

{

for i=1,..,S

=define nearest neighbour(x);

for all y

if (fitness(x) > fitness(y

))

{

Z=Z+x;

};

The function b(x,z) can be easily evaluated by

defining if individual x is in a predefined radius of

basin centre z. The radius is a tunable parameter. In

this study, we define it as

=





(2)

where k is the number of identified basins (=



The second measure is called Sum of Distances

to Nearest Neighbour (SDNN). The SDNN penalizes

the clustering of solutions. This indicator does not

require knowledge of optima and basins. The SDNN

can be calculated as









=







,





(3)











,



=min

∈\















,



where d

is the distance to the nearest neighbour,

dist is the Hamming distance.

Finally, we combine the BR and the SDNN in an

integrated criterion K:

=∙1∙



(4)

where 

is a normalized value of , 

defines weights of the BR and the SDNN in the sum

(∈0,1.

Next, we need to design a scheme for the

redistribution of computational resources. New

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

population sizes are defined for each algorithm. In

this study, all algorithms give to the “winner”

algorithm a certain percentage of their population

size, but each algorithm has a minimum guaranteed

resource that is not distributed. The guaranteed

resource can be defined by the population size or by

problem features.

At the coopearative stage, in many

coevolutionary schemes, all individual algorithms

begin each new adaptation period with the same

starting points (such a migration scheme is called

“the best displaces the worst”). For MMO problems,

the best solutions are defined by discovered basins

in the search space. As we already have evaluated

the approximation of basins (Z), the solutions from Z

are introduced in all populations replacing the most

similar individuals.

Stop criteria in the SelfMMOGA are similar to

those in the standard GA: maximum number of

objective evaluations, the number of generations

with no improvement (stagnation), etc.

4 EXPERIMENTAL RESULTS

To estimate the approach performance we have used

the following list of benchmark problems:

 Six binary MMO problems are from (Yu and

Suganthan, 2010). These test functions are based

on the unitation functions, and they are

massively multimodal and deceptive.

 Eight real-valued MMO problems are from

CEC’2013 Special Session and Competition on

Niching Methods for Multimodal Function

Optimization (Li et al., 2013b).

Table 2: Test suite.

Problem

Number of desirable

optima

Problem

dimensionality*

binaryF11 32 global 30

binaryF12 32 global 30

binaryF13 27 global 24

binaryF14 32 global 30

binaryF15 32 global 30

binaryF16 32 global 30

cecF1 2 global + 3 local 9, 12, 15, 19, 22

cecF2 5 global 4, 7, 10, 14 ,17

cecF3 1 global + 4 local 4, 7, 10, 14 ,17

cecF4 4 global 14, 22, 28, 34, 42

cecF5 2 global + 2 local 11, 17, 24, 31, 37

cecF6 18 global + 742 local 16, 22, 30, 36, 42

cecF7 36 global 14, 20, 28, 34, 40

cecF8 12 global 8, 14, 20, 28, 34

* Real-valued problems have been binarized using the

standard binary encoding with 5 accuracy levels.

We have denoted the functions as in the source

papers. Some details of the problems are presented

in Table 2.

In all comparisons, all algorithms have equal

maximum number of the objective evaluations, but

may differ in population sizes.

The following criteria for estimating the

performance of the SelfMMOGA over the

benchmark problems are used for continuous

problems:

 Peak Ratio (PR) measures the percentage of all

optima found by the algorithm (Equation 5).

 Success Rate (SR) measures the percentage of

successful runs (a successful run is defined as a

run where all optima were found) out of all runs.

=

|

∈|



,

|



(5)

where =







,



,…,





is a set of known optima,

 is accuracy level.

The maximum number of function evaluation

and the accuracy level for the PR evaluation are the

same as in CEC completion rules (Li et al., 2013b).

The number of independent runs of the algorithm is

50.

In the case of binary problems, we cannot define

the accuracy level in the PR, thus the exact points in

the search space have to be found. This is a great

challenge for search algorithms, thus we have

substituted the SR measure with Peak Distance

(PD). The PD indicator calculates the average

distance of known optima to the nearest individuals

in the population (Preuss and Wessing, 2013).

=











,





(6)

To demonstrate the control of algorithm

interaction in the SelfMMOGA, we have chosen an

arbitrary run of the algorithm on the cecF1 problem

and have visualized the distribution of the

computational resource (see Figure 2). The total

population size is 200 and the minimal guaranteed

amount of the computational recourse is 10. The

maximum number of generations is 200 and the size

of the adaptation period is 10, thus the horizontal

axis contains numeration of 20 periods.

As we can see, there is no algorithm that wins all

the time. At the first two periods, Sharing (Alg2) and

Clearing (Alg1) had better performance. The highest

amount of the resource was won by Clustering

(Alg3) at the 10th period. At the final stages,

Deterministic Crowding showed better performance.

The results of estimating the performance of the

SelfMMOGA with the pack of binary problems are

Multi-Strategy Genetic Algorithm for Multimodal Optimization

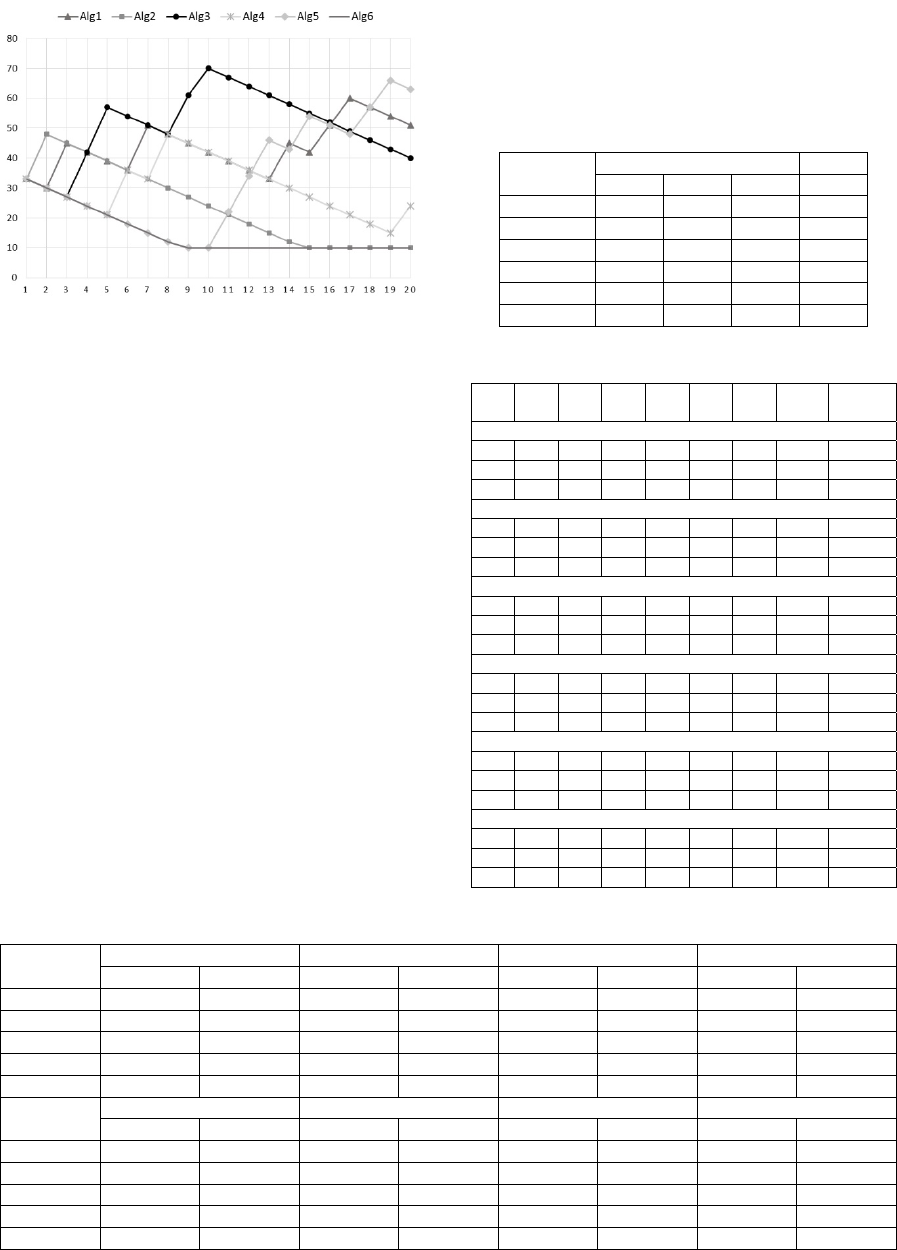
Figure 2: Example of the SelfMMOGA run.

presented in Table 3. The table contains the values

of the PR, the SR and the PD averaged over 50

independent runs. We also have compared the

results with Ensemble of niching algorithms (ENA)

proposed in (Yu and Suganthan, 2010). There is

only the SR value for the ENA.

The setting for the SelfMMOGA are:

 Maximum number of function evaluation is

50000 (as for the ENA);

 Total population size is 200 (the ENA uses 500);

 Adaptation period is 10 generations (25 times);

 All specific parameters of individual algorithms

are self-tunable using the concept from

(Semenkin and Semenkina, 2012).

As we can see, binary problems are not too

complex for the SelfMMOGA and the ENA.

Therefore we will analyze the results in details. In

Table 4, the results for stand-alone algorithms, the

average of 6 stand-alone algorithms and the

SelfMMOGA (6 algorithms ensemble) are

presented. The average value (“Mean” column) can

be viewed as the average performance of a randomly

chosen algorithm. Such an estimate is very useful for

black-box optimization problems, because we have

no information about problem features and,

consequently, about what algorithms to use. If the

performance of the SelfMMOGA is better that the

Table 3: Results for binary problems.

Problem

SelfMMOGA ENA

PR SR PD SR

binaryF11 1.00 1.00 0.00 1.00

binaryF12 1.00 1.00 0.00 1.00

binaryF13 1.00 1.00 0.00 1.00

binaryF14 1.00 1.00 0.00 1.00

binaryF15 1.00 1.00 0.00 1.00

binaryF16 1.00 1.00 0.00 0.99

Table 4: Detailed results for binary problems.

Alg1 Alg2 Alg3 Alg4 Alg5 Alg6 Mean

Self-

MMOGA

Problem: binaryF11

0.94 0.84 0.91 1.00 0.97 0.78 0.91 1.00

0.90 0.84 0.88 1.00 0.94 0.80 0.89 1.00

2.40 3.37 2.40 0.00 2.33 3.30 2.30 0.00

Problem: binaryF12

0.97 0.97 1.00 1.00 0.97 0.84 0.96 1.00

0.96 0.98 1.00 1.00 0.94 0.84 0.95 1.00

2.00 1.00 0.00 0.00 1.67 3.62 1.38 0.00

Problem: binaryF13

1.00 0.96 0.96 0.93 0.96 0.89 0.95 1.00

1.00 0.96 0.94 0.90 0.94 0.84 0.93 1.00

0.00 2.50 2.67 2.80 2.67 3.37 2.34 0.00

Problem: binaryF14

0.91 0.81 0.91 1.00 0.94 0.75 0.89 1.00

0.92 0.92 0.90 1.00 0.94 0.80 0.91 1.00

3.25 2.50 2.60 0.00 2.67 3.20 2.37 0.00

Problem: binaryF15

0.88 0.88 0.84 0.88 0.88 0.72 0.84 1.00

0.88 0.86 0.84 0.86 0.84 0.64 0.82 1.00

2.33 2.57 2.62 2.71 2.37 3.06 2.61 0.00

Problem: binaryF16

0.84 0.75 0.84 0.88 0.78 0.56 0.78 1.00

0.84 0.80 0.86 0.84 0.76 0.66 0.79 1.00

3.25 2.80 3.00 2.87 3.08 3.47 3.08 0.00

Table 5: The SelfMMOGA results (PR and SR) for continuous problems.

Accuracy

level ε

cecF1 cecF2 cecF3 cecF4

PR SR PR SR PR SR PR SR

1e-01 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000

1e-02 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000

1e-03 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000

1e-04 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000

1e-05 1.000 1.000 1.000 1.000 1.000 1.000 0.887 0.623

Accuracy

level ε

cecF5 cecF6 cecF7 cecF8

PR SR PR SR PR SR PR SR

1e-01 1.000 1.000 0.843 0.540 0.851 0.540 1.000 1.000

1e-02 1.000 1.000 0.834 0.536 0.792 0.223 1.000 1.000

1e-03 1.000 1.000 0.814 0.378 0.762 0.029 0.966 0.775

1e-04 1.000 1.000 0.560 0.140 0.731 0.000 0.964 0.753

1e-05 1.000 1.000 0.000 0.000 0.687 0.000 0.954 0.670

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

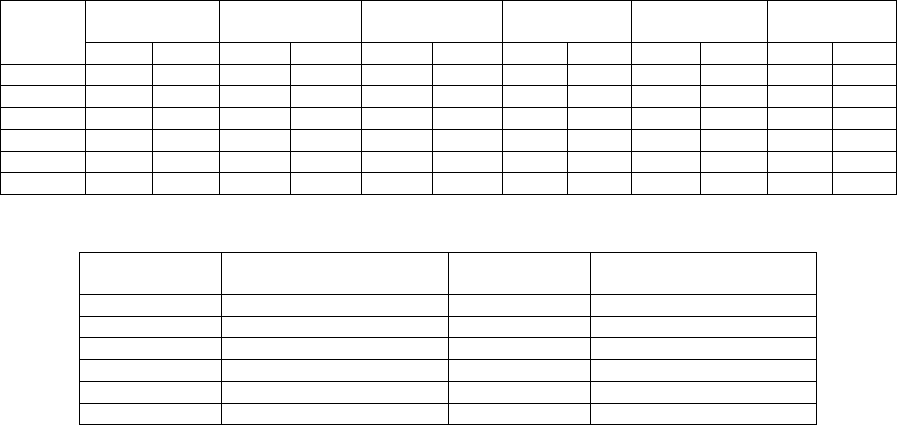
Table 6: Average PR and SR for each algorithm.

SelfMMOGA DE/nrand/1/bin cDE/rand/1/bin N-VMO dADE/nrand/1

PNA-

NSGAII

PR SR PR SR PR SR PR SR PR SR PR SR

1e-01 0.962 0.885 0.850 0.750 0.963 0.875 1.000 1.000 0.998 0.938 0.945 0.875

1e-02 0.953 0.845 0.848 0.750 0.929 0.810 1.000 1.000 0.993 0.828 0.910 0.750

1e-03 0.943 0.773 0.848 0.748 0.847 0.718 0.986 0.813 0.984 0.788 0.906 0.748

1e-04 0.907 0.737 0.846 0.750 0.729 0.623 0.946 0.750 0.972 0.740 0.896 0.745

1e-05 0.816 0.662 0.792 0.750 0.642 0.505 0.847 0.708 0.835 0.628 0.811 0.678

Average 0.916 0.780 0.837 0.750 0.822 0.706 0.956 0.854 0.956 0.784 0.893 0.759

Table 7: Algorithms ranking over cecF1-cecF8 problems.

Rank by

PR criterion

Algorithm

Rank by

SR criterion

Algorithm

1 N-VMO and dADE/nrand/1 1 N-VMO

2 SelfMMOGA 2 dADE/nrand/1

3 PNA-NSGAII 3 SelfMMOGA

4 DE/nrand/1/bin 4 PNA-NSGAII

5 cDE/rand/1/bin 5 DE/nrand/1/bin

- - 6 cDE/rand/1/bin

average of its component, we can conclude that on

average the choice of the SelfMMOGA will be

better.

As we can see from Table 4, the SelfMMOGA

always outperforms the average of its stand-alone

component algorithms for binary problems.

Moreover, for problems F15 and F16 no stand-alone

algorithm has a SR value equal to 1, but the

SelfMMOGA does.

The results of estimating the performance of the

SelfMMOGA with the pack of continuous problems

are presented in Tables 5-6. Table 5 shows detailed

results, Table 6 shows a comparison of average

values with other techniques and Table 7 contains

ranks of algorithms by separate criteria.

All problems and settings are as in the rules of

the CEC’13 competition on MMO. For each

problem there are 5 levels of accuracy of finding

optima (={1e-01, 1e-02,…, 1e-05}). Thus, each

problem have been binarized 5 times. The

dimensionalities of binarized problems are presented

in Table 2.We have also compared the results of the

SelfMMOGA runs with some efficient techniques

from the competition. The techniques are

DE/nrand/1/bin and Crowding DE/rand/1/bin (Li et

al., 2013b), N-VMO (Molina et al., 2013),

dADE/nrand/1 (Epitropakis et al., 2013), and PNA-

NSGAII (Bandaru and Deb, 2013).

The settings for the SelfMMOGA are:

 Maximum number of function evaluation is

50000 (for cecF1-cecF5) and 200000 (for cecF6-

cecF8);

 Total population size is 200;

 Adaptation period is 10 generations 25 times (for

cecF1-cecF5) and 25 generations 40 times

(cecF6-cecF8);

 All specific parameters of individual algorithms

are self-tunable.

As we can see from Tables 5-7, the

SelfMMOGA shows results comparable with

popular and well-studied techniques. It yields to

dADE/nrand/1 and N-VMO, but we should note that

these algorithms are specially designed for

continuous MMO problems, and have taken 2nd and

4th places, respectively, in the CEC competition. At

the same time, the SelfMMOGA has very close

average values to the best two algorithms, and

outperforms PNA-NSGAII, CrowdingDE and DE,

which have taken 7th, 8th and 9th places

respectively.

In this study, we have included only basic MMO

search techniques in the SelfMMOGA.

Nevertheless, it performs well due to the effect of

collective decision making in the ensemble. The key

feature of the approach is that it operates in an

automated, self-configuring way. Thus, the

SelfMMOGA can be a good alternative for complex

black-box MMO problems.

5 CONCLUSIONS

In this study, a novel genetic algorithm (called

SelfMMOGA) for multimodal optimization is

proposed. It is based on self-configuring

metaheuristic, which involves many different search

Multi-Strategy Genetic Algorithm for Multimodal Optimization

strategies in the process of MMO problem solving

and adaptively control their interactions.

The SelfMMOGA allows complex MMO

problems to be dealt with, which are the black-box

optimization problems (a priori information about

the objective and its features are absents or cannot

be introduces in the search process). The algorithm

uses binary representation for solutions, thus it can

be implemented for many real-world problems with

variables of arbitrary (and mixed) types.

We have included 6 basic MMO techniques in

the SelfMMOGA realization to demonstrate that it

performs well even with simple core algorithms. We

have estimated the SelfMMOGA performance with

a set of binary benchmark MMO problems and

continuous benchmark MMO problems from

CEC’2013 Special Session and Competition on

Niching Methods for Multimodal Function

Optimization. The proposed approach has

demonstrated a performance comparable with other

well-studied techniques.

Experimental results show that the SelfMMOGA

outperforms the average performance of its stand-

alone algorithms. It means that it performs better on

average than a randomly chosen technique. This

feature is very important for complex black-box

optimization, where the researcher has no possibility

of defining a suitable search algorithm and of tuning

its parameters. The proposed approach does not

require the participation of the human-expert,

because it operates in an automated, self-configuring

way.

In further works, we will investigate the

SelfMMOGA using more advanced component

techniques.

ACKNOWLEDGEMENTS

The research was supported by President of the

Russian Federation grant (MK-3285.2015.9). The

author expresses his gratitude to Mr. Ashley

Whitfield for his efforts to improve the text of this

article.

REFERENCES

Bandaru, S. and Deb, K., 2013. A parameterless-niching-

assisted bi-objective approach to multimodal

optimization. Proc. 2013 IEEE Congress on

Evolutionary Computation (CEC’13). pp. 95-102.

Bessaou, M., Petrowski, A. and Siarry, P., 2000. Island

Model Cooperating with Speciation for Multimodal

Optimization. Parallel Problem Solving from Nature

PPSN VI, Lecture Notes in Computer Science, Volume

1917. pp. 437-446.

Das, S., Maity, S., Qub, B.-Y. and Suganthan, P.N., 2011.

Real-parameter evolutionary multimodal optimization:

a survey of the state-of-the art. Swarm and

Evolutionary Computation 1, pp. 71–88.

Deb, K. and Saha, A., 2010. Finding Multiple Solutions

for Multimodal Optimization Problems Using a Multi-

Objective Evolutionary Approach. Proceedings of the

12th Annual Conference on Genetic and Evolutionary

Computation, GECCO 2010. ACM, New York. pp.

447-454.

Epitropakis, M.G., Li, X. and Burke, E.K., 2013. A

dynamic archive niching differential evolution

algorithm for multimodal optimization. Proc. 2013

IEEE Congress on Evolutionary Computation

(CEC’13). pp. 79-86.

Li, X., Engelbrecht, A. and Epitropakis, M., 2013a.

Results of the 2013 IEEE CEC Competition on

Niching Methods for Multimodal Optimization.

Report presented at 2013 IEEE Congress on

Evolutionary Computation Competition on: Niching

Methods for Multimodal Optimization.

Li, X., Engelbrecht, A. and Epitropakis, M.G., 2013b.

Benchmark functions for CEC’2013 special session

and competition on niching methods for multimodal

function optimization. Evol. Comput. Mach. Learn.

Group, RMIT University, Melbourne, VIC, Australia.

Tech. Rep.

Liu, Y., Ling, X., Shi, Zh., Lv, M., Fang. J. and Zhang, L.,

2011. A Survey on Particle Swarm Optimization

Algorithms for Multimodal Function Optimization.

Journal of Software, Vol. 6, No. 12. pp. 2449-2455.

Molina, D., Puris, A., Bello, R. and Herrera, F., 2013.

Variable mesh optimization for the 2013 CEC special

session niching methods for multimodal optimization.

Proc. 2013 IEEE Congress on Evolutionary

Computation (CEC’13). pp. 87-94.

Preuss, M. and Wessing, S., 2013. Measuring multimodal

optimization solution sets with a view to

multiobjective techniques. EVOLVE – A Bridge

between Probability, Set Oriented Numerics, and

Evolutionary Computation IV. AISC, vol. 227,

Springer, Heidelberg. pp. 123–137.

Preuss, M., 2014. Tutorial on Multimodal Optimization. In

the 13th International Conference on Parallel

Problem Solving from Nature, PPSN 2014, Ljubljana,

Slovenia.

Preuss, M., Stoean, C. and Stoean, R., 2011. Niching

foundations: basin identification on fixed-property

generated landscapes. Proceedings of the 13th Annual

Conference on Genetic and Evolutionary

Computation, GECCO 2011. pp. 837–844.

Qu, B., Liang, J., Suganthan P.N. and Chen, T., 2012.

Ensemble of Clearing Differential Evolution for Multi-

modal Optimization. Advances in Swarm Intelligence

Lecture Notes in Computer Science, Volume 7331. pp.

350-357.

Semenkin, E.S. and Semenkina, M.E., 2012. Self-

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

configuring Genetic Algorithm with Modified

Uniform Crossover Operator. Advances in Swarm

Intelligence. Lecture Notes in Computer Science 7331.

Springer-Verlag, Berlin Heidelberg. pp. 414-421.

Singh, G. and Deb, K., 2006. Comparison of multi-modal

optimization algorithms based on evolutionary

algorithms. In Proceedings of the Genetic and

Evolutionary Computation Conference, Seattle. pp.

1305–1312.

Sopov, E., 2015. A Self-configuring Metaheuristic for

Control of Multi-Strategy Evolutionary Search. ICSI-

CCI 2015, Part III, LNCS 9142. pp. 29-37.

Yu, E.L. and Suganthan, P.N., 2010. Ensemble of niching

algorithms. Information Sciences, Vol. 180, No. 15.

pp. 2815-2833.

Multi-Strategy Genetic Algorithm for Multimodal Optimization