Weighting and Sampling Data for Individual Classifiers and Bagging
with Genetic Algorithms
Sa
ˇ
so Karakati
ˇ
c, Marjan Heri
ˇ
cko and Vili Podgorelec
Institute of Informatics, UM FERI, Smetanova 17, Maribor, Slovenia
Keywords:
Classification, Genetic Algorithm, Instance Selection, Weighting, Bagging.
Abstract:
An imbalanced or inappropriate dataset can have a negative influence in classification model training. In
this paper we present an evolutionary method that effectively weights or samples the tuples from the train-
ing dataset and tries to minimize the negative effects from innaprotirate datasets. The genetic algorithm with
genotype of real numbers is used to evolve the weights or occurrence number for each learning tuple in the
dataset. This technique is used with individual classifiers and in combination with the ensemble technique of
bagging, where multiple classification models work together in a classification process. We present two vari-
ations – weighting the tuples and sampling the classification tuples. Both variations are experimentally tested
in combination with individual classifiers (C4.5 and Naive Bayes methods) and in combination with bagging
ensemble. Results show that both variations are promising techniques, as they produced better classification
models than methods without weighting or sampling, which is also supported with statistical analysis.
1 INTRODUCTION
Supervised machine learning methods, such as classi-
fication, use a process of learning where a computer
is presented with a set of solved tuples (classification
instances with known results). This set is called a
train dataset and its purpose is to help with classi-
fication model creation. The quality of the resulting
machine learning model is heavily dependent on the
tuples from the train dataset, where a proper train set
helps with the creation of a good model, but inappro-
priate train tuples can misguide the learning algorithm
and prevent it from reaching the optimal solutions.
Inappropriate train datasets can harm the model
creation in following ways (Stefanowski and Wilk,
2008), (Japkowicz and Stephen, 2002):
• Mislabeled tuples. Mislabeling can be a result of
a human or machine error and force the learning
process to result in false conclusions. The model
is then built upon a false presentation of reality
and does not perform well on real problems.
• Imbalanced datasets. The nature of machine
learning algorithms is such that they learn in a
way that minimizes the errors. Over representa-
tion of a certain class of individuals can harm this
process. More specifically, big differences in fre-
quencies of classes can cause the algorithm to in-
tentionally ignore or under-emphasize the minori-
ties.
• Outliers. Outliers are individuals that are not nec-
essary in a minority class but are nonetheless low
in frequency in certain properties. This situation
where some attributes of individuals are heavily
outnumbered can cause algorithms to ignore some
important aspects of the dataset or misinterpret it
for an error.
Several techniques exist which can help to over-
come the problem of inappropriate train dataset. First
body of techniques is gathered under an umbrella
term of instance selection methods (Liu, 2010). The
theory of instance selection methods postulates that
we can select some individuals from original train
dataset that are then used to train the model. There
are numerous variations on how the training subset is
selected.
Another approach to solve the problem is with the
use of ensemble methods (Dietterich, 2000), where
multiple classification models cooperate together to
form a final solution. But again all classifiers in the
ensemble are prone to (although to a lesser extent)
error based on the inappropriate train datasets.
We propose a novel method to solve this problem
of inappropriate train datasets, which can be used by
any individual classifier or in combination with en-
180
Karakati
ˇ
c, S., Heri
ˇ
cko, M. and Podgorelec, V..
Weighting and Sampling Data for Individual Classifiers and Bagging with Genetic Algorithms.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 180-187
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
semble method bagging. Our method is applied in
the pre-processing part of learning process and uses a
genetic algorithm to construct the train dataset by ei-
ther subsample and oversample, or weighing the clas-
sification tuples. Two interesting variations arise and
are presented this paper: sampling the train data and
weighting the train data. The proposed method is
tested on individual classifiers as with bagging en-
semble method, to determine the effectiveness and
potential usefulness of the method.
The rest of the paper is constructed as follows.
The second section takes an overview of related work
from the body of relevant literature of instance selec-
tion and train dataset preparation. Next, the third sec-
tion presents the genetic algorithm that is used in our
method. Multiple variations of the genetic algorithm
are presented: for individual classifiers, for ensem-
bles, with sampling and with weighting. Fourth sec-
tion is dedicated to the experiments with our method
and its variations where we make comparisons with
traditional classification methods and ensemble tech-
niques, to determine the quality of our method. After
that we conclude the paper with a discussion of results
and possible future development on the subject.
2 RELATED WORK
There have been numerous studies done on rebalanc-
ing the datasets with the goal of achieving better final
outcomes of classification. Most of these are done
with instance selection from the datasets, where the
method of selections generates the subset of original
dataset and then uses it in classification model. For a
good overview of these methods refer to a survey on
tuple selection methods (Olvera-L
´
opez et al., 2010).
Selection methods are divided in categories:
• Wrapper methods. These methods use the classi-
fication metrics to determine which tuples should
be selected for final subset of tuples. Usual metric
used here is overall classification accuracy.
• Filter methods. This method uses some other met-
ric or function that is not based on the classifica-
tion results.
Our method of sampling and weighting is a wrap-
per approach as it uses classification accuracy as a
metric for selection. Next we follow up with the re-
view of relevant literature on wrapper methods, espe-
cially in combination with evolutionary methods.
Main tuple selection approaches are based on
the nearest neighbor (NN) methods, such as con-
densed NN (Angiulli, 2005), selective NN (Linden-
baum et al., 2004) and generalized condensed NN
(Chou et al., 2006). These methods use a method of
finding the nearest neighbors to remove the unwanted
tuples that are either too similar to one and another or
by removing dense clusters of tuples from the dataset.
An extension of regular NN methods are IB2 and IB3
algorithms, that incrementally removes or preserves
missclassified tuples by 1-NN algorithm (Wilson and
Martinez, 2000).
Evolutionary algorithms have also been used
for the tuple selection wrapper methods. There
are numerous methods based on genetic algo-
rithms (Kuncheva and Bezdek, 1998), (Bezdek and
Kuncheva, 2001) and (Cano et al., 2003). All of these
methods use an array of 0 and 1 in arrays, where
each gene represents the absence (0) or presence (1)
of each classification tuple. As described later in
section 3 this genotype representation is very simi-
lar to our approach, but we extend this by allowing
genes to have integers larger then 1, thus not just se-
lecting a tuple but effectively sampling data with re-
placements. Our method uses the same genetic op-
erators as have been used in this literature, as our
goal was to present novel genotype representation and
not to find optimal operator settings. One interest-
ing method used genetic algorithms in combination
with neural networks to select optimal subset of orig-
inal train dataset (Kim, 2006). In another paper re-
searchers used genetic algorithm for feature and tuple
selection (Tsai et al., 2013), but used GA to determine
which method should they use. Another combination
of kNN method and GA is used in a paper (Garca-
Pedrajas and Prez-Rodrguez, 2012).
The problem with these selection methods is
that they only remove individuals from the original
dataset, but they do not repeat instance occurrence in
the dataset it this would provide any additional im-
provements. Tuple selection technique can thus be de-
fined as an undersampling method, but research show
that random undersampling (removing tuples on ran-
dom) (Kotsiantis and Pintelas, 2003) can lead to in-
formation loss and consequently to less than optimal
classification models (Japkowicz, 2000), (Japkowicz
and Stephen, 2002), (Kubat and Matwin, 1997). In a
paper (Cateni et al., 2014) researchers use a combi-
nation of undersampling the majorities and oversam-
pling the minority tuples to achieve an equilibrium
and improved classification. Oversampling and un-
dersampling at the same time is usually called sam-
pling dataset with replacements, where an algorithm
selects desired number of tuples and they can repeat
in the new dataset.
Sampling with replacements (or even without
them) is used in some ensemble methods, such as bag-
ging (Breiman, 1996), where a chosen amount of new
Weighting and Sampling Data for Individual Classifiers and Bagging with Genetic Algorithms
181

datasets are sampled from the original train dataset.
Each of these new datasets is then used as a train set
for a classification method. Each classifier then pro-
duces a slightly different model which then partici-
pates in an ensemble. The final decision of an en-
semble is determined by a majority vote from all of
the models in an ensemble. In it’s original form, the
bagging method selects bags (sampled datasets) by
simple uniform random fashion. Later in section 4
we also use our method in combination with the bag-
ging method. Our contribution to the field is that our
method also builds the bags in a such way, that the
whole ensemble is more efficient in basic classifica-
tion metrics.
Weighting tuples is a similar process to sampling,
but instead of duplicating or removing tuples we as-
sign weights to them, where a higher weight implies
a higher importance and a lower weight denotes less
important tuples. Weighting tuples is done in boosting
algorithms, such as AdaBoost (Freund et al., 1996).
We can reproduce weighting in sampling form, where
the ratio between weights is the same as the ration be-
tween the frequency of tuple occurrence. This is done
in combination with methods that cannot work with
weighted datasets. Nonetheless, weighting is prefer-
able to sampling because it uses less computation re-
sources (no redundant computation necessary for du-
plicated tuples). Weighting tuples have also been
done in (Zhao, 2008), (Ting, 2002), (Liu et al., 2013),
(Liu and Yu, 2007) and (Cano et al., 2013). We also
use weights in tuples in one variation of our method,
but the main difference from sampling method is not
ratio, but the weight and frequency distribution, as
will be presented in the next section.
3 GENETIC ALGORITHMS FOR
WEIGHTING AND SAMPLING
Genetic algorithm (GA) is a method in the field of
evolutionary computation and can be used on vari-
ous optimization problems. GA mimics the process
of evolution and natural selection where population
is guided with fitness functions to its final goal. It
has been proposed by Holland in his work Adaptation
in Natural and Artificial System (Holland, 1992) and
many variations have been made since then.
Population in GA is a set of individuals where
each individual represents the solution to a given
problem. In our case we dealt with the sampling and
weighting of train dataset, so the genotype of one in-
dividual is constructed from an array of numbers (see
figure 1). Each gene is linked with one tuple from the
train dataset. Gene with index of i represents a tuple
Figure 1: Top – array genotype for sampling variation. Each
gene value represents the occurrence number for each tuple.
Bottom – array genotype for weighting variation. Each gene
value represents the weight for each tuple.
with index i from the dataset. Here we are given two
options on how to construct our genotype. In the case
of sampling we can use an array of integers where
each gene shows the number of occurrences of a given
tuple from the dataset. The default case without sam-
pling would be the array of all genes set to 1, as each
tuple is in our dataset once. When gene value is set
to 0 that tuple is not present in a train set and does
not play a role in training of a classification model.
Naturally the genes can have integers higher than 1,
meaning that tuples are duplicated so their number is
the same as the value of its gene. The initialization of
this type of genotype is done as the random number
from the set with normal distribution with the mean
on 1 and the standard deviation as the changing pa-
rameter. Note that example occurrences in the dataset
can not be set as the negative number, which means
that random executes again until the resulting number
is valid.
The second option of individuals representation
is for weighting tuples, where genotype is an array
of real numbers where the numbers are weights as
shown in figure 1. Weights in gene say how much
importance is given to it’s linked tuple – the higher
the number, more important is that particular tuple.
Again, if any given gene has a value set to zero weight
it means that it does not participate in the training of
the model. The real difference from the previously
described genotype is with the initialization of the
genes. Each weight (gene value) is randomly chosen
from the set of number in [0, 1] in an uniform distri-
bution.
These two variations of the genotype are also used
in a combination with the bagging method. With bag-
Figure 2: Genotype and phenotype for bagging method.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
182
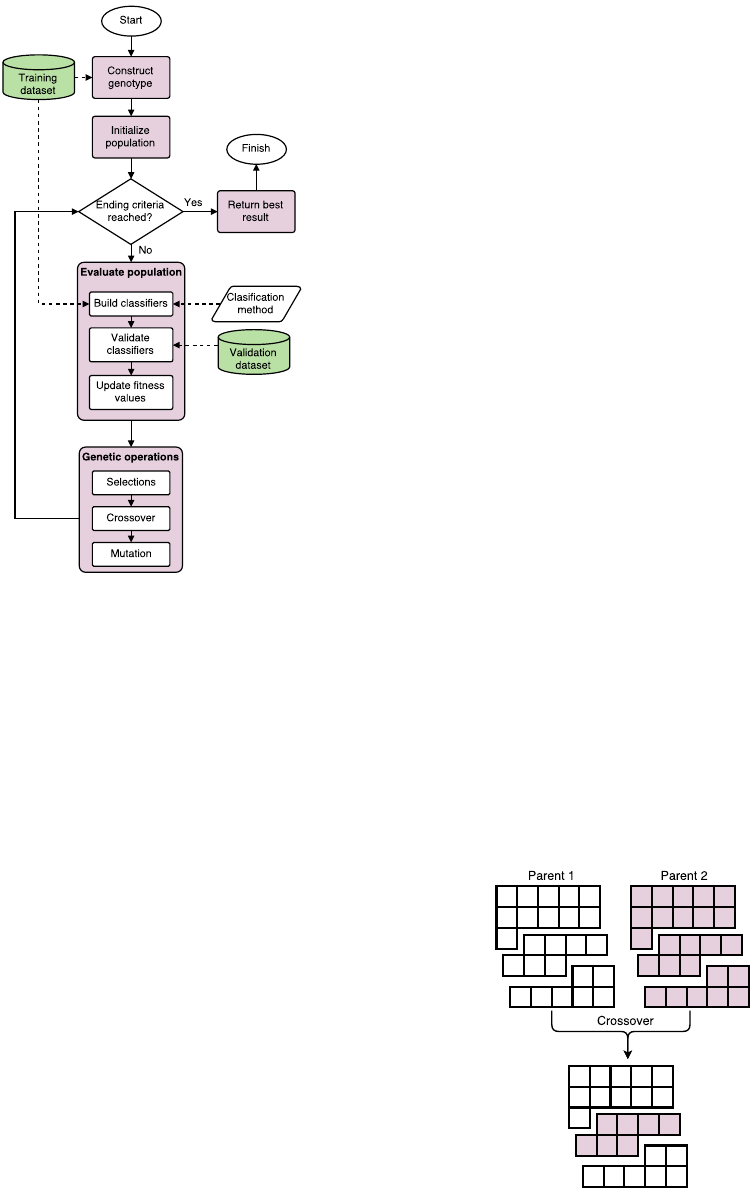
Figure 3: Flowchart of the whole evolutionary process.
Note that Classification method presents an algorithm for
building classification model.
ging we have multiple different sets (bags), which can
overlap or be disjointed. The extensions of genotypes
for bagging is such that the array is repeated for each
bag. Figure 2 presents the genotype and its transfor-
mation to the phenotype (note that only sampling vari-
ation is shown in the figure, but the representation is
the same for weighting in bagging).
The basic flowchart of GA methods is depicted in
figure 3 and goes as follows. First the initial popula-
tion is generated – each individual solution is made
in the process described previously. Then we eval-
uate each individual solution with the fitness func-
tion. Calculating the fitness levels starts with build-
ing a classification model with a chosen classifica-
tion method on sampled or weighted train dataset and
evaluating it on the validation dataset. Classification
metric error rate of the built model is used as the fit-
ness value, which means that the fitness function tries
to minimize it’s value and ideally hit zero.
After the evaluation the selection process starts.
Here we use a standard binary tournament method
which randomly chooses two individual solutions
from the population and selects the one with a bet-
ter value. Selected solutions are then paired and go
through a genetic operator of crossover, where both
parent solutions contribute a part of their genotype
to form a new child solution. The ordered crossover
(OX) is used, also known as a two-point crossover.
Here, two points between genes are selected, same in
both parents, and the part between two points are ex-
changed. This results in two offspring solutions that
continue through the process of evolution. This kind
of crossover is used in a combination with individ-
ual classifiers or with bagging. As figure 4 shows,
some bags are copied whole, but some bags can be cut
and can include genes from both parents. This forces
changing of individual bags and not only combination
of bags, which would be the case if only whole bags
were mixed in the crossover process.
The resulting children have a small chance to go
through a genetic operator of mutation, where one
gene is randomly selected and it’s value is changed
to a random value with the same method as is used
for the creation of the genotypes. When the mutation
is finished, children solutions then form a new popu-
lation and form a basis for the next generation.
4 EXPERIMENTS
In this section we present the results of our experi-
ments. All four variations of our method have been
used in the experiments:
• Sampling for single classifiers
• Weighting for single classifiers
• Sampling for Bagging
• Weighting for Bagging
These methods were tested in combination with
traditional classification methods: C4.5 (Quinlan,
1993) and Naive Bayes (John and Langley, 1995).
Figure 4: Ordered crossover for bagging ensemble. Some
bags can be cut in two parts – this forces evolution of indi-
vidual bags, as well as mixing of different bags.
Weighting and Sampling Data for Individual Classifiers and Bagging with Genetic Algorithms
183
Our method was also compared to models trained on
original datasets and on bagging.
We used 11 standard classification benchmark
datasets from UCI repository (Lichman, 2013), which
have been divided in the following way: 60% for
training, 20% for validation and 20% for testing. The
datasets were split in a random fashion and this pro-
cess was repeated 5 times, in order to minimize the
possibility for false conclusions. This is similar to us-
ing 5 fold cross validation, but instead of using 4 fold
for training and 1 fold for testing, we used 3 folds for
training, 1 for validation and 1 for testing. Same splits
(folds) were used on all of the methods, to insure en-
sure the comparability of the results.
The settings for genetic algorithm were as fol-
lows: 100% chance of ordered crossover, 10% chance
of random exchange mutation, population of 100 in-
dividual, 200 generations and binary tournament se-
lection. The bagging method used an ensemble of
5 classification models (5 bags). The genetic algo-
rithm and experimental setup were programmed in
Java programming language and used in combination
with Weka machine learning framework.
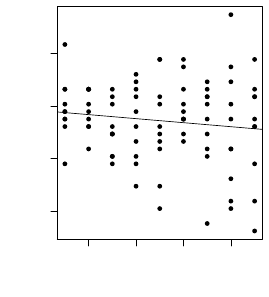
4.1 Spread of Sampling
In the first experiment we tried to determine whether
there are any significant differences in models when
initialization process of genes uses a different stan-
dard deviation for random generator based on normal
distribution. The experiment was made with bagging
and base classifier C4.5 and the use of sampling vari-
ation of our method. In figure 5 we see a liner regres-
sion model where we look at the accuracy metric.
1 2 3 4
0.65 0.70 0.75 0.80
Standard deviation
Overall classification accuracy
Figure 5: Trend of changing standard deviation in the ini-
tialization of genes for sampling variation.
The slope of the trend line indicates a slight de-
cline in the overall accuracy as standard deviation in-
creases, but is enough that we use standard deviation
of 1 for further experiments as it produces ac-
curate and least volatile results.
4.2 Experiments with Traditional
Classification Methods
Here we compare our method with the traditional
classification methods in combination with both sam-
pling and weighting. In table 1 we see the resulting
accuracy and average F-score of C4.5 method. All
of the results are averaged on all of the folds, which
is standard in a cross-validation process. We first
identified the distribution type of the results and then
continued with the appropriate tests. None of the re-
sults had normal distribution (both Shapiro-Wilk and
Kolmogorov-Smirnov tests return p < 0.05) so we
used non-parametric tests for the comparison. First
Friedman’s Two-Way ANOVA was used to determine
if there are significant differences between all com-
pared groups. If ANOVA confirmed the differences,
we continued with post-hoc where we used Wilcoxon
signed-rank test (non-parametric alternative to t-test
for related samples) and Holm-Bonferroni correction
(correction for multiple comparison to reduce the
chance of a Type I error).
There are differences in accuracies between the
methods, but these differences are not statistically
significant as shown by the Friedman’s Two-Way
ANOVA for related samples (p
acc
= 0.120). On
the other hand the differences in the F-scores have
reached statistical significance (p
f sc
= 0.011). Post-
hoc test with the Holm-Bonferonni correction show
that there are statistically significant differences be-
tween C4.5 and sampling with C4.5 (p = 0.008), while
differences C4.5 vs weighting and weighting vs sam-
pling are not significant (p = 0.110 and p = 0.674 re-
spectively). Based on the presented results (the me-
dian value and the Friedman ranks) we can conclude
that our two variation are at least as good and can even
be better as C4.5 without our methods.
Next we made the same experiment with Naive
Bayes methods and results are shown in table 2. In all
but two datasets our methods achieved better results in
comparison to classifier without sampling or weight-
ing. In one case (iris dataset) the results were tied.
Although there are no statistically significant differ-
ences in either of the metric (p
acc
= 0.154 and p
f sc
= 0.115) we can see a trend in the resulting metrics.
Best median value and the highest Friedman rank was
achieved by sampling method in both metrics.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
184

Table 1: Accuracy and F-score results on all benchmarks for C4.5 and two variations of our method with C4.5. Accuracies
are averaged across folds. Bolded values show the best results for given metric in particular dataset.
C4.5 Sampling Weighting
Accuracy F-score Accuracy F-score Accuracy F-score
autos 0,7343 0,7278 0,7829 0,7786 0,7229 0,7107
balance-scale 0,7714 0,7514 0,7590 0,7533 0,7829 0,7533
breast-cancer 0,7104 0,6764 0,7292 0,7111 0,7167 0,6889
car 0,9003 0,8992 0,9038 0,9052 0,8788 0,8755
credit-a 0,8391 0,8393 0,8400 0,8399 0,8609 0,8608
diabetes 0,7227 0,7140 0,7359 0,7349 0,7398 0,7321
heart-c 0,7510 0,7471 0,7569 0,7555 0,7843 0,7828
heart-statlog 0,7667 0,7645 0,7800 0,7795 0,8022 0,7995
iris 0,9320 0,9320 0,9440 0,9437 0,9360 0,9360
primary-tumor 0,3982 0,3462 0,3982 0,3749 0,3807 0,3144
vehicle 0,7177 0,7124 0,7156 0,7124 0,7241 0,7194
Median 0.7510 0.7471 0.7590 0.7555 0.7829 0.7533
Friedman Rank 1.50 1.32 2.23 2.55 2.27 2.14
Table 2: Accuracy and F-score results on all benchmarks for Naive Bayes and two variations of our method with Naive Bayes.
Accuracies are averaged across folds. Bolded values show the best results for given metric in particular dataset.
Naive Bayes Sampling Weighting
Accuracy F-score Accuracy F-score Accuracy F-score
autos 0.5486 0.5470 0.5743 0.5586 0.5857 0.5731
balance-scale 0.8857 0.8462 0.8886 0.8558 0.8886 0.8514
breast-cancer 0.7208 0.7094 0.7229 0.7150 0.7125 0.6939
car 0.8378 0.8256 0.8604 0.8519 0.8806 0.8712
credit-a 0.7704 0.7612 0.8070 0.8031 0.8061 0.8012
diabetes 0.7383 0.7350 0.7422 0.7368 0.7633 0.7575
heart-c 0.8412 0.8404 0.8627 0.8625 0.8373 0.8367
heart-statlog 0.8533 0.8526 0.8489 0.8481 0.8467 0.8464
iris 0.9520 0.9519 0.9520 0.9519 0.9520 0.9512
primary-tumor 0.4754 0.4411 0.4614 0.4148 0.4474 0.4016
vehicle 0.4298 0.3868 0.5184 0.5049 0.4858 0.4634
Median 0.7704 0.7612 0.8070 0.8031 0.8061 0.8012
Friedman Rank 1.64 1.68 2.41 2.50 1.95 1.82
4.3 Experiments with Bagging
Ensemble
In this section we present the results of the experi-
ments on the bagging ensemble method. Again we
used 11 benchmark sets from the previous experi-
ment. Experiments with bagging were repeated on
the previously used classification methods: C4.5 and
Naive Bayes. The results where we again aggregated
the resulting metrics from all folds in the same value.
In table 3 the results for bagging with C4.5 are
presented. The statistical analysis shows that there
are significant differences in the accuracy and aver-
age F-score (p
acc
= 0.013 ; p
f sc
= 0.013). In post-
hoc test for accuracy we see that sampling variation
is superior to both the basic bagging and the sam-
pling method (for both p = 0.022). The results for
F-score are similar – the sampling method resulted in
superior solutions when compared to both, weighting
and basic methods (both p = 0.022). Table 4 presents
Figure 6: Comparing sum of Friedman’s Ranks. Higher is
better.
the results for bagging with Naive Bayes base classi-
fier and we can see that our method (both variations)
achieve better results in all ten datasets. Statistical
tests (Friedman’s ANOVA) shows that there are sig-
nificant differences in both metrics (p
acc
= 0.002 ; p
f sc
= 0.012). Further post-hoc tests (Wilcoxon signed-
Weighting and Sampling Data for Individual Classifiers and Bagging with Genetic Algorithms
185
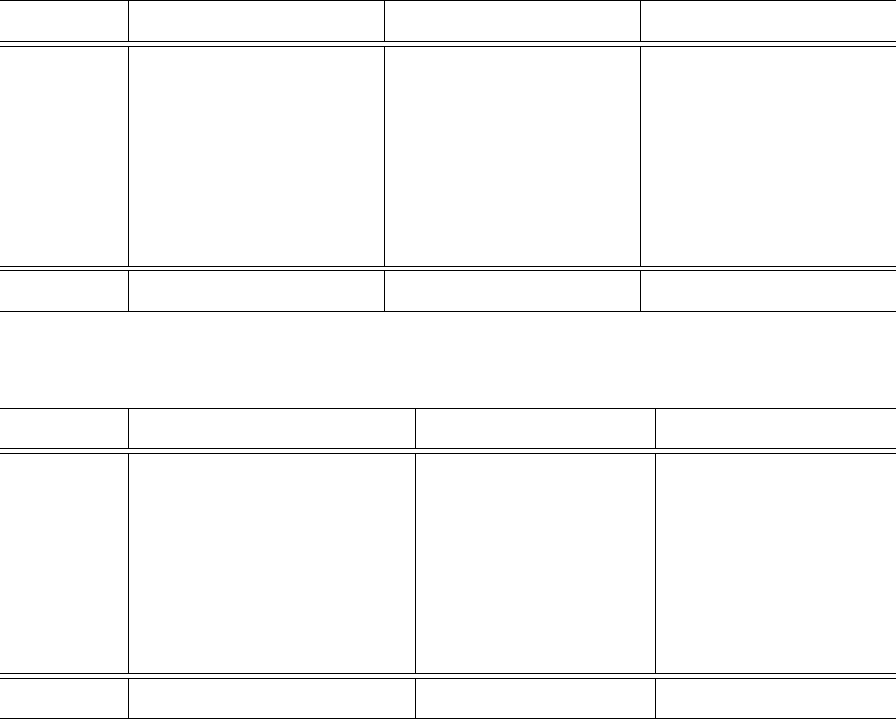
Table 3: Accuracy and F-score results on all benchmarks datasets for Bagging with base classifier C4.5. Comparison between
our two variations with Bagging (C4.5) and default bagging without sampling or weighting. Accuracies are averaged across
folds. Bolded values show the best results for given metric in particular dataset.
Bagging with C4.5 Sampling Weighting
Accuracy F-score Accuracy F-score Accuracy F-score
autos 0.7343 0.7276 0.8086 0.6886 0.8075 0.6691
balance-scale 0.7971 0.7817 0.8048 0.8229 0.7874 0.7881
breast-cancer 0.7000 0.6613 0.7375 0.7208 0.7062 0.6806
car 0.9090 0.9086 0.9382 0.8972 0.9387 0.8905
credit-a 0.8513 0.8507 0.8504 0.8652 0.8499 0.8651
diabetes 0.7305 0.7259 0.7344 0.7438 0.7279 0.7382
heart-c 0.7706 0.7691 0.7745 0.7765 0.7732 0.7746
heart-statlog 0.7933 0.7914 0.7800 0.8156 0.7772 0.8136
iris 0.9640 0.9638 0.9680 0.9440 0.9679 0.9439
primary-tumor 0.3860 0.3514 0.4140 0.4281 0.3819 0.3549
vehicle
0.7220 0.7167 0.7504 0.7241 0.7461 0.7166
Median 0.7706 0.7691 0.7800 0.7765 0.7772 0.7746
Friedman Rank 1.64 1.64 2.73 2.73 1.64 1.64
Table 4: Accuracy and F-score results on all benchmarks datasets for Bagging with base classifier Naive Bayes. Comparison
between our two variations with Bagging (Naive Bayes) and default bagging without sampling or weighting. Accuracies are
averaged across folds. Bolded values show the best results for given metric in particular dataset.
Bagging with Naive Bayes Sampling Weighting
Accuracy F-score Accuracy F-score Accuracy F-score
autos 0.5686 0.5550 0.6057 0.5928 0.6000 0.5880
balance-scale 0.8857 0.8465 0.8933 0.8537 0.8990 0.8590
breast-cancer 0.7250 0.7190 0.7292 0.7146 0.7354 0.7255
car 0.8413 0.8297 0.8535 0.8433 0.8587 0.8473
credit-a 0.7757 0.7668 0.7817 0.7740 0.8017 0.7961
diabetes 0.7500 0.7423 0.7516 0.7451 0.7594 0.7550
heart-c 0.8333 0.8330 0.8353 0.8352 0.8510 0.8496
heart-statlog 0.8333 0.8321 0.8311 0.8297 0.8356 0.8344
iris 0.9480 0.9476 0.9400 0.9394 0.9640 0.9638
primary-tumor 0.4807 0.4424 0.4842 0.4460 0.4807 0.4256
vehicle 0.4390 0.3952 0.4965 0.4688 0.4504 0.4115
Median 0.7757 0.7668 0.7817 0.7740 0.8017 0.7961
Friedman Rank 1.23 1.36 2.09 2.00 2.68 2.64
rank test with Holm-Bonferroni correction) for accu-
racies reveal that the significant differences exist be-
tween our weighting method and the basic method (p
= 0.002), while differences between the basic method
and sampling variation are not significant (p = 0.086).
The same post-hoc analysis was done for the F-score
metric and again there are statistical significant differ-
ences between the basic bagging (with Naive Bayes)
and our weighting method (p = 0.006).
5 CONCLUSIONS
We presented an evolutionary method for manipu-
lating the training dataset in two variations with the
hopes of producing better classification models. Both
variations are based on genetic algorithm where the
genotype represents the number of occurrences or
weights of any particular tuple. We can conclude,
based on the results, that our methods for individual
classifiers of sampling and weighting can produce re-
sults that are at least as good (and in some cases bet-
ter) as the method without them. In the metrics we
see improvements, but these differences are mostly
not statistically significant. On the other hand, our
methods for bagging produce major improvements on
both metrics and these improvements are significant,
which means that our genetic algorithm indeed helps
with the construction of better models. In figure 6 we
compare sum of the ranks of all variations included
in the experiment. The higher sum indicates better
results in different conditions (with different classi-
fiers). The sampling variation has the highest sum of
ranks and is followed by weighting variation of our
method. This indicates that the sampling variation is
superior to weighting and to original (no sampling nor
weighting) in context of our experiment. Further ex-
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
186
amination of the sum of ranks reveals that the weight-
ing variation was still preferred in combination with
bagging and Naive Bayes. This means that there is
no universally best variation – as it is expected in the
field of classification, where universally best classifier
cannot exist.
Further work will include using our methods with
more classification algorithms, to determine what
kind of algorithms work better with sampling or
weighting and how to choose appropriate variation.
Future work could also include the usage of other
metrics for evaluation in our fitness function.
REFERENCES
Angiulli, F. (2005). Fast condensed nearest neighbor rule.
In Proceedings of the 22Nd International Conference
on Machine Learning, ICML ’05, pages 25–32, New
York, NY, USA. ACM.
Bezdek, J. C. and Kuncheva, L. I. (2001). Nearest proto-
type classifier designs: An experimental study. Inter-
national Journal of Intelligent Systems, 16(12):1445–
1473.
Breiman, L. (1996). Bagging predictors. Machine learning,
24(2):123–140.
Cano, A., Zafra, A., and Ventura, S. (2013). Weighted data
gravitation classification for standard and imbalanced
data. Cybernetics, IEEE Transactions on, 43(6):1672–
1687.
Cano, J. R., Herrera, F., and Lozano, M. (2003). Using
evolutionary algorithms as instance selection for data
reduction in kdd: an experimental study. Evolutionary
Computation, IEEE Transactions on, 7(6):561–575.
Cateni, S., Colla, V., and Vannucci, M. (2014). A method
for resampling imbalanced datasets in binary classifi-
cation tasks for real-world problems. Neurocomput-
ing, 135(0):32 – 41.
Chou, C.-H., Kuo, B.-H., and Chang, F. (2006). The gen-
eralized condensed nearest neighbor rule as a data re-
duction method. In Pattern Recognition, 2006. ICPR
2006. 18th International Conference on, volume 2,
pages 556–559. IEEE.
Dietterich, T. G. (2000). Ensemble methods in machine
learning. In Multiple classifier systems, pages 1–15.
Springer.
Freund, Y., Schapire, R. E., et al. (1996). Experiments with
a new boosting algorithm. In ICML, volume 96, pages
148–156.
Garca-Pedrajas, N. and Prez-Rodrguez, J. (2012). Multi-
selection of instances: A straightforward way to im-
prove evolutionary instance selection. Applied Soft
Computing, 12(11):3590 – 3602.
Holland, J. H. (1992). Adaptation in natural and artificial
systems: an introductory analysis with applications to
biology, control, and artificial intelligence. MIT press.
Japkowicz, N. (2000). The class imbalance problem: Sig-
nificance and strategies. In Proc. of the Intl Conf. on
Artificial Intelligence. Citeseer.
Japkowicz, N. and Stephen, S. (2002). The class imbalance
problem: A systematic study intelligent data analysis.
John, G. H. and Langley, P. (1995). Estimating continuous
distributions in bayesian classifiers. In Proceedings
of the Eleventh conference on Uncertainty in artificial
intelligence, pages 338–345. Morgan Kaufmann Pub-
lishers Inc.
Kim, K.-j. (2006). Artificial neural networks with evo-
lutionary instance selection for financial forecasting.
Expert Systems with Applications, 30(3):519–526.
Kotsiantis, S. and Pintelas, P. (2003). Mixture of expert
agents for handling imbalanced data sets. Annals of
Mathematics, Computing & Teleinformatics, 1(1):46–
55.
Kubat, M. and Matwin, S. (1997). Addressing the curse of
imbalanced data sets: One sided sampling. In Proc. of
the Int’l Conf. on Machine Learning.
Kuncheva, L. I. and Bezdek, J. C. (1998). Nearest proto-
type classification: clustering, genetic algorithms, or
random search? Systems, Man, and Cybernetics, Part
C: Applications and Reviews, IEEE Transactions on,
28(1):160–164.
Lichman, M. (2013). UCI machine learning repository.
Lindenbaum, M., Markovitch, S., and Rusakov, D. (2004).
Selective sampling for nearest neighbor classifiers.
Machine learning, 54(2):125–152.
Liu, H. (2010). Instance selection and construction for data
mining. Springer-Verlag.
Liu, J.-F. and Yu, D.-R. (2007). A weighted rough set
method to address the class imbalance problem. In
Machine Learning and Cybernetics, 2007 Interna-
tional Conference on, volume 7, pages 3693–3698.
Liu, X.-Y., Li, Q.-Q., and Zhou, Z.-H. (2013). Learning
imbalanced multi-class data with optimal dichotomy
weights. In Data Mining (ICDM), 2013 IEEE 13th
International Conference on, pages 478–487.
Olvera-L
´
opez, J. A., Carrasco-Ochoa, J. A., Mart
´
ınez-
Trinidad, J. F., and Kittler, J. (2010). A review of
instance selection methods. Artificial Intelligence Re-
view, 34(2):133–143.
Quinlan, J. R. (1993). C4.5: programs for machine learn-
ing. Elsevier.
Stefanowski, J. and Wilk, S. (2008). Selective pre-
processing of imbalanced data for improving classi-
fication performance. In Song, I.-Y., Eder, J., and
Nguyen, T., editors, Data Warehousing and Knowl-
edge Discovery, volume 5182 of Lecture Notes in
Computer Science, pages 283–292. Springer Berlin
Heidelberg.
Ting, K. M. (2002). An instance-weighting method to in-
duce cost-sensitive trees. Knowledge and Data Engi-
neering, IEEE Transactions on, 14(3):659–665.
Tsai, C.-F., Eberle, W., and Chu, C.-Y. (2013). Ge-
netic algorithms in feature and instance selection.
Knowledge-Based Systems, 39(0):240 – 247.
Wilson, D. R. and Martinez, T. R. (2000). Reduction tech-
niques for instance-based learning algorithms. Ma-
chine learning, 38(3):257–286.
Zhao, H. (2008). Instance weighting versus threshold ad-
justing for cost-sensitive classification. Knowledge
and Information Systems, 15(3):321–334.
Weighting and Sampling Data for Individual Classifiers and Bagging with Genetic Algorithms
187
