Gaussian Process for Regression in Business Intelligence:

A Fraud Detection Application

Bruno H. A. Pilon

, Juan J. Murillo-Fuentes

, Jo

ao Paulo C. L. da Costa

Rafael T. de Sousa J

unior

and Antonio M. R. Serrano

Department of Electrical Engineering, University of Brasilia (UnB), Brasilia - DF, Brazil

Department of Signal Theory and Communications, University of Sevilla, Sevilla, Spain

Keywords:

Gaussian Processes, Business Intelligence, Fraud Detection.

Abstract:

Business Intelligence (BI) systems are designed to provide information to support the decision making process

in companies and governmental institutions. In this scenario, future events depend on the decisions and on the

previous events. Therefore, the mathematical analysis of past data can be an important tool for the decision

making process and to detect anomalies. Depending on the amount and the type of data to be analyzed,

techniques from statistics, Machine Learning (ML), data mining and signal processing can be used to automate

all or part of the system. In this paper, we propose to incorporate Gaussian Process for Regression (GPR) in BI

systems in order to predict the data. As presented in this work, fraud detection is one important application of

BI systems. We show that such application is possible with the use of GPR in the predictive stage, considering

that GPR natively returns a full statistical description of the estimated variable, which can be used as a trigger

measure to classify trusted and untrusted data. We validate our proposal with real world BI data provided by

the Brazilian Federal Patrimony Department (SPU), regarding the monthly collection of federal taxes. In order

to take into account the multidimensional structure of this speciﬁc data, we propose a pre-processing stage for

reshaping the original time series into a bidimensional structure. The resulting algorithm, with GPR at its core,

outperforms classical predictive schemes such as Artiﬁcial Neural Network (ANN).

1 INTRODUCTION

Gaussian process for regression (GPR) is a widely

used family of stochastic process schemes for mod-

eling dependent data, primarily due to two essen-

tial properties that dictate the behavior of the pre-

dicted variable. First, a Gaussian process is com-

pletely determined by its mean and covariance func-

tion, which reduces the amount of parameters to be

speciﬁed since only the ﬁrst and second order mo-

ments of the process are needed. Second, the pre-

dicted values are a function of the observed values,

where all ﬁnite-dimensional distribution sets have a

multivariate Gaussian distribution.

In a BI environment, the fact that GPR returns a

complete statistical description of the predicted vari-

able can add conﬁdence to the ﬁnal result and help the

evaluation of its performance. Additionally, the statis-

tical description can be used as a trigger to transform

a regression problem into a classiﬁcation problem de-

pending on the context (Williams and Barber, 1998).

When dealing with multidimensional data, GPR can

be independently modeled in each dimension, which

adds ﬂexibility for data sets with different degrees of

correlation among its dimensions.

In this work, GPR is used to model the amount of

tax collected monthly by the Brazilian Federal Patri-

mony Department (SPU)

. The regression model pro-

posed estimates the amount to be collected at a given

month in the future. Considering that the time series

provided by SPU possess a multidimensional struc-

ture, we propose a pre-processing stage to reshape the

original data set into a bidimensional structure.

This paper is organized as follows. In Sec-

tion 2, the motivation and related works are intro-

duced, showing the relevance of the proposed method

and the state-of-the-art schemes in the literature. In

Section 3, a review of techniques related to GPR is

presented. In Section 4, a unidimensional GPR based

predictor model is developed. In Section 5, a method

for reshaping the original data set is proposed, allow-

ing the application of GPR in a bidimensional data

In Portuguese, Secretaria do Patrim

onio da Uni

ao.

Pilon, B., Murillo-Fuentes, J., Costa, J., Júnior, R. and Serrano, A..

Gaussian Process for Regression in Business Intelligence: A Fraud Detection Application.

In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 3: KMIS, pages 39-49

ISBN: 978-989-758-158-8

set. In Section 6, a technique for optimizing the hy-

perparameters of the GPR’s covariance function is

presented and the resulting experimental prediction is

included. Finally, in Section 7, conclusions and con-

siderations are drawn.

2 MOTIVATION AND RELATED

WORK

The development process of a BI system involves

concepts from many different knowledge ﬁelds. In a

nutshell, BI systems aims to collect, organize, analyze

and share data from different sources, giving them a

useful meaning.

In the context of BI systems, fraud detection

schemes are continuously evolving. In 2012, global

credit, debit and prepaid card fraud losses reach

$11.27 billion (Robertson, 2013). Of that, card issuers

lost 63% and merchants lost the other 37% (Robert-

son, 2013).

When a new fraud detection scheme becomes pub-

lic domain, criminals are likely to use this informa-

tion to evade themselves off this type of detection,

limiting the public exchange of ideas regarding this

topic (Bolton and Hand, 2002).

The need for fast and efﬁcient algorithms makes

automated statistical fraud detection schemes widely

varied, but there are common features. Essentially,

those methods compare observed or estimated data

with expected values (Bolton and Hand, 2002).

Predictive fraud detection approaches have been

used in (Dorronsoro et al., 1997), where an ANN

is used for fraud detection in credit card operations;

in (Serrano et al., 2012), where an ANN based predic-

tor was used in real world BI data for forecasting and

heuristics based on error metrics decides if the pre-

dicted data is possibly fraudulent or regular. In (Nagi

et al., 2008), supported vector machines and genetic

algorithms are used to identify electricity theft.

3 GAUSSIAN PROCESS FOR

REGRESSION

Gaussian processes belong to the family of stochastic

processes that can be used for modeling dependent

data observed over time and/or space (Rasmussen and

Williams, 2006). In this paper, the main interest is

on supervised learning, which can be characterized

by a function that maps the input-output relationship

learned from empirical data, i.e. a training data set. In

this study, the output function is the amount of tax to

be collected at any given month by SPU, and hence a

continuous random variable.

In order to make predictions based on a ﬁnite data

set, a function h needs to link the known sets of the

training data with all the other possible sets of input-

output values. The characteristics of this underly-

ing function h can be deﬁned in a wide variety of

ways (Bernardo et al., 1998), and that is where Gaus-

sian processes are applied. Stochastic processes, as

the Gaussian process, dictate the properties of the un-

derlying function as well as probability distributions

govern the properties of a random variable (Rasmussen

and Williams, 2006).

Two properties make Gaussian processes an inter-

esting tool for inference. First, a Gaussian process

is completely determined by its mean and covariance

functions, requiring only the ﬁrst and second order

moments to be speciﬁed, which makes it a non para-

metric model whose structure is ﬁxed and completely

known. Second, the predictor of a Gaussian process is

based on a conditional probability and can be solved

with simple linear algebra, as shown in (Davis, 2001).

3.1 Gaussian Process

Multivariate Gaussian distributions are useful for mod-

eling ﬁnite collections of real-valued random variables

due to their analytical properties. Gaussian processes

extend this scenario, evolving from distributions over

random vectors to distributions over random functions.

A stochastic process is a collection of random

variables, e.g. {h(x) : x ∈ X }, deﬁned on a cer-

tain probability space and indexed by elements from

some set (Cinlar, 2013). Just as a random variable as-

signs a real number to every outcome of a random ex-

periment, a stochastic process assigns a sample func-

tion to every outcome of a random experiment (Cinlar,

2013).

A Gaussian process is a stochastic process where

any ﬁnite subcollection of random variables has a

multivariate Gaussian distribution. In other words, a

collection of random variables {h(x) : x ∈ X } is

a Gaussian process with mean function m(·) and co-

variance function k(·, ·) if, for any ﬁnite set of ele-

ments {x

, x

, . . . , x

∈ X }, the associated ﬁnite set

of random variables h(x) have a distribution of the

form













m(x

)

m(x

)













k(x

, x

) · · · k(x

, x

)

k(x

, x

) · · · k(x

, x

)













(1)

The notation for deﬁning h(x) as a Gaussian pro-

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

cess is

h(x) ∼ GP(m(x), k(x, x

)), (2)

for any x and x

∈ X . The mean and covariance

functions are given, respectively, by:

m(x) = E[x],

k(x, x

) = E[(x − m(x))(x

− m(x

))];

(3)

also for any x and x

∈ X .

Intuitively, a sample function h(x) drawn from a

Gaussian process can be seen as an extremely high di-

mensional vector obtained from an extremely high di-

mensional multivariate Gaussian, where each dimen-

sion of the multivariate Gaussian corresponds to an

element x

from the index X , and the corresponding

component of the random vector represents the value

of h(x

) (Rasmussen and Williams, 2006).

3.2 Regression Model and Inference

Let S = {(x

, y

)}

i=1

, x ∈ R

and y ∈ R, be

a training set of independent identically distributed

(iid) samples from some unknown distribution. In

its simplest form, GPR models the output nonlinearly

by (P

erez-Cruz et al., 2013):

= h(x

) + ν

; i = 1, . . . , m (4)

where h(x) ∈ R

. An additive iid noise variable

ν ∈ R

, with N (0, σ

), is used for noise modeling.

Other noise models can be seen in (Murray-Smith and

Girard, 2001). Assume a prior distribution over func-

tion h(·) being a Gaussian process with zero mean:

h(·) ∼ GP(0, k(·, ·)), (5)

for some valid covariance function k(·, ·) and, in ad-

dition, let T = {

, by

)}

i=1

x ∈ R

and by ∈ R, be a

set of iid testing points drawn from the same unknown

distribution S.

Given the training data S, the prior distribution

h(·) and the testing inputs

X, the use of standard

tools of Bayesian statistics such as the Bayes’ rule,

marginalization and conditioning allow the computa-

tion of the posterior predictive distribution over the

testing outputs by (Rasmussen and Williams, 2006).

Deriving the conditional distribution of

y results

in the predictive equations of GPR. Please refer

to (Rasmussen and Williams, 2006) for further de-

tails:

y|y, X,

X ∼ N (µ

[1]

, Σ

[1]

), (6)

where

[1]

= K(

X, X)[K(X, X) + σ

−1

[1]

= K(

X)+

I − K(

X, X)[K(X, X) + σ

−1

K(X,

X).

Since a Gaussian process returns a distribution

over functions, each of the inﬁnite points of the func-

tion

y have a mean and a variance associated with

it . The expected or most probable value of

y is its

mean, whereas the conﬁdence about that value can be

derived from its variance.

3.3 Covariance Functions

In the previous section, it was assumed that the covari-

ance function k(·, ·) is known, which is not usually

the case. In fact, the power of the Gaussian process to

express a rich distribution on functions rests solely on

the shoulders of the covariance function (Snoek et al.,

2012), if the mean function can be set or assumed to

be zero. The covariance function deﬁnes similarity

between data points and its form determines the pos-

sible solutions of GPR (P

erez-Cruz et al., 2013).

A wide variety of families of covariance functions

exists, including squared exponential, polynomial, etc.

See (Rasmussen and Williams, 2006) for further de-

tails. Each family usually contains a number of free

hyperparameters, whose value also need to be deter-

mined. Therefore, choosing a covariance function for

a particular application involves the tuning of its hy-

perparameters (Rasmussen and Williams, 2006).

The covariance function must be positive semi-

deﬁnite, given that it represents the covariance ma-

trix of a multivariate Gaussian distribution (P

erez-

Cruz et al., 2013). It is possible to build compos-

ite covariance functions by adding simpler covariance

functions, weighted by a positive hyperparameter, or

by multiplying them, as adding and multiplying posi-

tive deﬁnite matrices results in a positive deﬁnite ma-

trix (P

erez-Cruz et al., 2013).

One of the most commonly used covariance func-

tion in GPR is the squared exponential kernel given

by (7), which reﬂects the prior assumption that the la-

tent function to be learned is smooth (Blum and Ried-

miller, 2013).

k(x, x

) = σ

· exp



−

(x − x

)

2θ



. (7)

In a nutshell, the hyperparameter σ controls the

overall variance of the kernel function and the hy-

perparameter θ controls the distance from which two

points will be uncorrelated, both of them presented

in (7). These free parameters allow a ﬂexible cus-

tomization of the problem at hand (Blum and Ried-

miller, 2013), and maybe selected by inspection or

automatically tuned by ML using the training data set.

The covariance function in GPR plays the same

role as the kernel function in other approaches such

as Support Vector Machines (SVM) and kernel ridge

Gaussian Process for Regression in Business Intelligence: A Fraud Detection Application

regression (KRR) (P

erez-Cruz and Bousquet, 2004).

Typically, these kernel methods use cross-validation

techniques to adjust its hyperparameters (P

erez-Cruz

et al., 2013), which are highly computational demand-

ing and essentially consists of splitting the training set

into k disjoint sets and evaluate the probability of the

hyperparameters (Rasmussen and Williams, 2006).

On the other hand, GPR can infer the hyperpa-

rameters from samples of the training set using the

Bayesian framework (P

erez-Cruz et al., 2013). The

marginal likelihood of the hyperparameters of the ker-

nel given the training data set can be deﬁned as:

p(y|X) =

p(y|f , X)p(f|X)df. (8)

Recalling that X is dependent of the hyperpa-

rameter’s set, (Williams and Rasmussen, 1996) pro-

poses to maximize the marginal likelihood in (8) in

order to obtain the optimal setting of the hyperpa-

rameters. Although setting the hyperparameters by

maximum likelihood is not a purely Bayesian solu-

tion, it is fairly standard in the community and it al-

lows using Bayesian solutions in time sensitive ap-

plications (P

erez-Cruz et al., 2013). More detailed

information regarding practical considerations about

this topic will be presented in Subsection 6.1 and can

be seen in (MacKay, 2003).

4 UNIDIMENSIONAL GPR

PREDICTOR

The data set used along this work is the monthly

tax collection of SPU, ranging from years 2005 to

2010. The amount collected, expressed in reais

(R$), is treated as a random variable indexed by the

month, where x ranges from 1 to 72. Thus,

x = 1, . . . , 12 is related to the ﬁrst year’s collection

(2005); x = 13, . . . , 24 is related to the second year’s

collection (2006), and so forth.

For comparison purposes, it was used only the ﬁrst

60 months of the data (ranging from 2005 to 2009) to

build the covariance matrix and estimate the hyper-

parameters of the Gaussian process. The data regard-

ing the year 2010 was exclusively used to evaluate the

performance of the proposed predictor by error mea-

surement. Therefore, the ﬁrst ﬁve years of data will

be referred as the training data set, and the sixth year

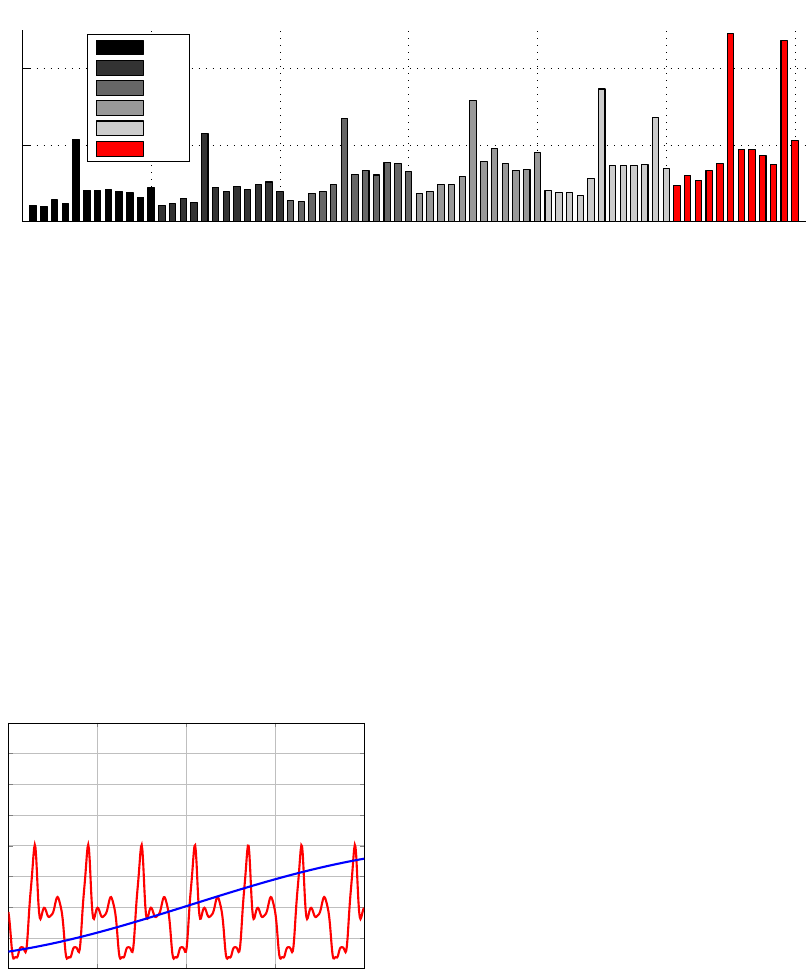
of data will be referred as the target data set. Figure 1

shows a bar plot of the data model used in this work.

In practice, a Gaussian process can be fully de-

ﬁned by just its second moment, or covariance func-

tion, if the mean function can be set or assumed to be

zero. The implications of that approach takes place

in Subsection 4.1, where the data normalization and

a unidimensional model for the mean and covariance

functions are discussed. The prediction results us-

ing this unidimensional model is presented in Subsec-

tion 4.2.

4.1 Mean and Covariance Function

Modeling

Considering the training SPU data set in Fig. 1, a pre-

processing stage normalized that data set by a mean

subtraction - transforming it into a zero mean data set

- and an amplitude reduction by a factor of one stan-

dard deviation. Thus, the mean function in (3) can be

set to zero and the focus of the GPR modeling can be

fully relied on the covariance function.

Some features of the training data are noticeable

by visual inspection, such as the long term rising trend

and the periodic component regarding seasonal vari-

ations between consecutive years. Taking those char-

acteristics into account, a combination of some well

known covariance functions is proposed in order to

achieve a more complex one, which is able to handle

those speciﬁc data set characteristics.

The uptrend component of the data set was mod-

eled by the following linear covariance function:

(x, x

) = x

. (9)

A closer examination of the data set reveals that,

yearly, there is a peak in the tax collection. Addition-

ally, for the years of 2005 and 2006, the peak occurred

in the ﬁfth month (May), whereas from 2007 to 2010

the peak occurred in the sixth month (June). The shift

of this important data signature makes the seasonal

variations not to be exactly periodic. Therefore, the

periodic covariance function

2,1

(x, x

) = σ

exp

−

2 sin

[

(x − x

)]

is modiﬁed by the squared exponential covariance

function

2,2

(x, x

) = exp



−

(x − x

)

2θ



resulting in the following covariance function to

model the seasonal variations:

(x, x

) = k

2,1

· k

2,2

(10)

Finally, the sum of the characteristic components

in (9) and (10), also with a measured noise assumed

to be additive white Gaussian with variance σ

leads

to the proposed noisy covariance function:

k(x, x

) = k

(x, x

) + k

(x, x

) + σ

I. (11)

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

12 24 36 48 60 72

x 10

2005

2006

2007

2008

2009

2010

Figure 1: Monthly tax collected by SPU, in reais (R$), indexed by the x

month. The gray scale bars, representing the years

between 2005 and 2009, were chosen as the training set, and the red bars, representing the year 2010, were chosen as the

target set.

In (11), the hyperparameter σ

gives the magni-

tude, or scaling factor, of the covariance function. The

and θ

give the relative length scale of periodic and

squared exponential functions, respectively, and can

be interpreted as a ”forgetting factor”. The smaller

the values of θ

1,3

, the more uncorrelated two given

observations x and x

are. The θ

, on the other hand,

controls the cycle of the periodic component of the

covariance function, forcing that underlying function

component to repeat itself after θ

time indexes.

As an example of the individual contributions of

each component of the covariance function to the ﬁ-

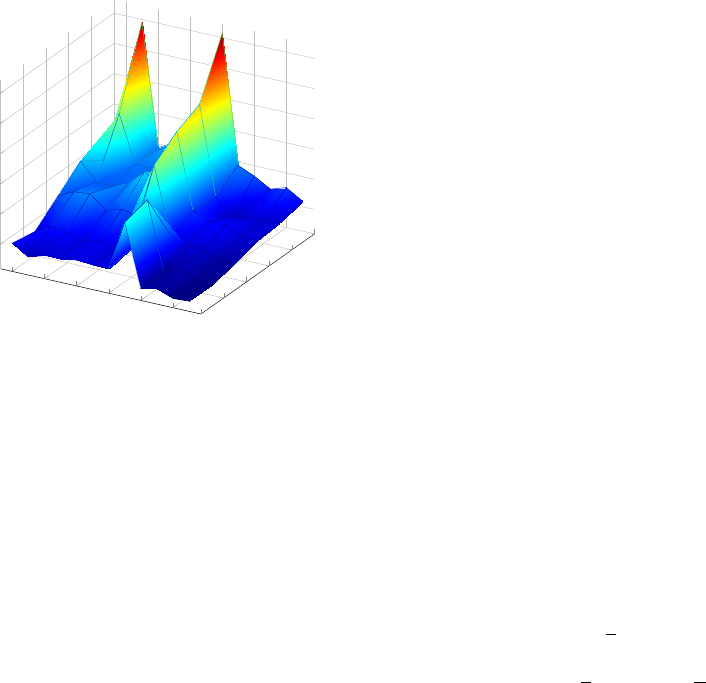
nal prediction, Fig. 2 shows the decomposed product

function k

(x, x

) of (10) in terms of the periodic and

the squared exponential components. The input ob-

served data is the normalized SPU data set in Fig. 1.

0 20 40 60 80

−1

−0.5

0.5

1.5

2.5

Month

k(x,x’)

Figure 2: Normalized plot of the posterior inference of

the Gaussian process, indexed by a continuous time inter-

val X = [0, 80], obtained using the covariance function

2,1

(x, x

) in red (the periodic component) and k

2,2

(x, x

)

in blue (the squared exponential component).

The plots of Fig. 2 were obtained with the hyper-

parameters

= 1; θ

= 0.3; θ

= 12; θ

= 60 and σ

= 0.1.

The magnitude σ

was set to 1 not to distort the

resulting function regarding the training set; the θ

was set to 0.3 month due to the poor month-to-month

correlation that the data presents; the θ

was set to

12 months due the periodicity of the data; the θ

was

set to 60 months to ensure all data points are taken

into account in the ﬁnal prediction results and, at least,

the σ

was set to 0.1 to add some white Gaussian

noise on the observation set. At this point, it is impor-

tant to remember that the initial choice of hyperpa-

rameters have only taken into consideration the char-

acteristics of the original data set. Later, on Subsec-

tion 6.1, we present a optimization method for tuning

them.

4.2 Unidimensional Prediction Results

With the covariance function deﬁned in (11) and a set

of training points given by the ﬁrst 60 months of the

normalized SPU data of Fig. 1, it is possible to for-

mulate a GPR with time as input.

The GPR’s characteristic of returning a probabil-

ity distribution over a function enables the evaluation

of the uncertainty level of a given result. For each

point of interest, the Gaussian process can provide the

expected value and the variance of the random vari-

able, as shown in Fig. 3.

It is noticeable that, for the twelve month predic-

tion using the proposed model, two predicted months

fell off the conﬁdence band that delimitates the 95%

certainty interval - June and November. These two

months have a high contribution on the overall pre-

diction error on this initial approach.

5 BIDIMENSIONAL DATA

RESHAPE

In this section, we propose a pre-processing stage

based on the cross-correlation proﬁle of the original

Gaussian Process for Regression in Business Intelligence: A Fraud Detection Application

0 10 20 30 40 50 60 70

−1.3

1.3

2.6

3.9

Month

k(x,x’)

Figure 3: Prediction results from conditioning the posterior

Gaussian jointly distribution at a continuous time interval

X = [0, 75]. The blue dots are the training data, the red

dots are the target data, the black tick line is the expected

value at a time index and the gray band represents the 95%

conﬁdence interval (two standard deviations above and be-

low the expected value).

data set. This proﬁle is used to separate highly corre-

lated months into one dimension and poor correlated

months into a different dimension, leading to a two

dimensional structure. Subsection 5.1 shows an anal-

ysis of the time cross-correlation results and impli-

cations on the proposed model, and Subsection 5.2

shows the proposed reshaped data set.

5.1 Time Cross-correlation

Although the uptrend and the periodic seasonal char-

acteristics are prominent in our data set, some impor-

tant features of the data are not visible at ﬁrst sight.

Considering that the covariance function used to de-

ﬁne the GPR is based on a measure of distance, where

closer pairs of observation points tend to have a strong

correlation and distant pairs of points tend to have a

weak correlation, a measure of month-to-month cor-

relation in SPU data can reveal the accuracy of that

approach.

The cross-correlation between two any inﬁnite

length sequences (Orfanidis, 2007) is given by

(m) = E[x

∗

n−m

]. In practice, sequences

x and y are likely to have a ﬁnite length, therefore the

true cross correlation needs to be estimated since only

partial information about the random process is avail-

able. Thus, the estimated cross-correlation, with no

normalization, can be calculated by (Orfanidis, 2007):

(m)











N−m−1

n=0

n+m

∗

if m ≥ 0

∗

(−m) if m < 0

(12)

Fig. 4 shows a plot of the absolute cross-

correlation of the entire SPU data as sequence x

, and

the last year’s target data as sequence y

. The smaller

sequence was zero-padded to give both sequences the

same length. The resulting cross-correlation was also

normalized to return 1.0 exactly where the lag m

matches the last year’s target data month-by-month.

0 12 24 36 48 60 72

0.2

0.4

0.6

0.8

Month

R(m)

Figure 4: Estimated absolute normalized cross-correlation

between the target data and the whole SPU data set. The

sequence was trimmed due to the zero-padding, and the red

circles highlight where the lag m is a multiple of 12 months.

The cross-correlation between the target data and

the rest of the sequence exhibited a couple of interest-

ing features about the data. First, it can be noted that

the ﬁrst two years are poorly correlated with the last

year. Second, there are some clear peaks on the cross-

correlation function where the lag m is a multiple of

12.

Some important conclusions arise from those fea-

tures. First one is that there is not much information

about the last year on the ﬁrst two years of data, and

the amount of information rises as it gets closer to the

target. This complies with the distance based correla-

tion function previously proposed.

Also, the peaks pattern shows that the month-to-

month correlation is poor, since we only get high cor-

relation values when comparing January of 2010 with

January of 2009, 2008, 2007; February of 2010 with

February of 2009, 2008, 2007 and so forth. Although

some secondary order correlation peaks can be noted,

their correlation are smaller than the noisy ﬁrst two

years, leading to the assumption that they do not pro-

vide much information.

5.2 Dataset Reshape

With the objective of incorporating the knowledge ob-

tained from the time cross-correlation showed in the

previous subsection, some changes were made in the

overall modeling proposed. An exponential proﬁle

shows a good approximation for modeling the cross-

correlation peaks, although the vicinity of the peaks

demonstrates a very low correlation with the target

data.

In spite the fact that an exponential proﬁle is the

main characteristic of the squared exponential covari-

ance function, for it to be a good approximation the

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

exponential proﬁle is required to be present at all

times. In this case, the cross-correlation proﬁle shows

that the tax collected 12 months before the prediction

is more correlated than the tax collected on the previ-

ous month of the prediction.

In order to take advantage of the squared exponen-

tial covariance function in translating the peaks corre-

lation proﬁle and, at the same time, to carry the char-

acteristics of the original data, this section proposes

to convert the original one dimensional SPU data into

a two dimensional array, with the ﬁrst dimension in-

dexed by month M = 1, 2, . . . , 12 and the second di-

mension indexed by year Y = 1, 2, . . . , 6. This leads

to a reshape of the 1D data of Fig. 1 into a 2D data

array presented at Fig. 5.

2,005

2,006

2,007

2,008

2,009

2,010

0.2

0.4

0.6

0.8

1.2

·10

Year

Month

Figure 5: Plot of the SPU data set converted in a 2D array.

With this new array as the input of our Gaus-

sian process, we can now separate the mean and the

covariance function in a two dimensional structure,

with different hyperparameters for it in each dimen-

sion. Considering the cross-correlation proﬁle of our

data shown in Subsection 5.1, we will assume that

only the amount of tax collected on January of 2005,

2006, 2007, 2008 and 2009 will inﬂuence the pre-

dictive quantity of tax collected in January of 2010,

and analogously to the other months. In other words,

the information used by the predictor will be obtained

exclusively from the highlights of Fig. 4. Therefore,

from this point forward, the selected approach is to

apply the ﬁnal covariance function showed in (11) ex-

clusively in the monthly dimension.

6 OPTIMIZATION AND RESULTS

This section describes the technique used to optimize

the hyperparameters of the proposed covariance func-

tion and the resulting prediction using the optimum

settings. In addition, we describe preliminary pro-

posals for a classiﬁcation stage aimed at future stud-

ies. In Subsection 6.1, the knowledge of the cross-

correlation proﬁle is applied into the covariance func-

tion model and the hyperparameters evaluation. In

Subsection 6.2, the bidimensional resulting predic-

tion is shown and in Subsection 6.3 a series of perfor-

mance measurements and error comparisons are made

with the previously obtained results, including com-

parisons with a similar approach using Neural Net-

works proposed in the literature and a usual ﬁnancial

estimating technique. In Subsection 6.4, a classiﬁca-

tion stage based on the statistical description of GPR

is discussed, labeling the data into regular or possibly

fraudulent.

6.1 Hyperparameters Tuning

Regarding the initial choice of the hyperparameters

and its tuning, that learning problem can be viewed

as an adaptation of the hyperparameters to a collec-

tion of observed data. Two techniques are usual for

inferencing their values in a regression environment:

i) the cross-validation and ii) the maximization of the

marginal likelihood.

Since our observed data possess a trend, split-

ting it would require some de-trending approach in

the pre-processing stage. Also, the number of train-

ing data points in this work is small, and the use of

cross-validation would lead to an even smaller train-

ing set (Rasmussen and Williams, 2006). Therefore,

the marginal likelihood maximization was chosen to

optimize the hyperparameter’s set.

The marginal likelihood of the training data is the

integral of the likelihood times the prior:

p(y|X) =

p(y|f , X)p(f|X)df. (13)

Recalling that X is dependent of the hyperparam-

eter’s set Θ, (Rasmussen and Williams, 2006) shows

that the log marginal likelihood can be stated as:

log p(y|X, Θ) = −

−1

y−

log |K

| −

log 2π.

(14)

In (14), K

= K

+ σ

I is the covariance matrix

of the noisy targets y and K

is the covariance matrix

of the noise-free latent f . To infer the hyperparam-

eters by maximizing the marginal likelihood in (13),

(Rasmussen and Williams, 2006) shows a numerically

stable algorithm that seeks the partial derivatives of

the logarithmic marginal likelihood in (14) with re-

spect to the hyperparameters.

Gaussian Process for Regression in Business Intelligence: A Fraud Detection Application

The methodology above described was used to

determine the optimum set of hyperparameters

Θ.

However, (Rasmussen and Williams, 2006) states two

problems regarding this approach. The ﬁrst one is

that the likelihood distribution is multimodal, i.e. is

dependent of the initial conditions of Θ. Also, the in-

version of the matrix K

is computationally complex.

In addition, our case presents another important

restriction. Our ﬁnal covariance function in (11) pos-

sess an hyperparameter θ

, one of the periodic co-

variance function’s hyperparameters, that dictates the

overall period of that function. As seen in Subsec-

tion 5.1, the optimum periodicity of the covariance

function should be within a ﬁnite set of multiples of

12, leading to

= {12, 24, 36, 48, 60}.

Imposing that restriction, the proposed algorithm

for hyperparameter’s optimization follows the se-

quence below:

• Deﬁne the initial values of the hyperparameter’s

set Θ;

• Evaluate the marginal likelihood of the periodic

component among the ﬁnite set of θ

, keeping the

other hyperparameters ﬁxed at their initial values;

• Choose the periodic hyerparameter with the max-

imum marginal likelihood;

• Evaluate the marginal likelihood of the resting hy-

perparameters, keeping the periodic hyperparam-

eter ﬁxed;

• Choose the ﬁnal set of hyperparameters with the

maximum marginal likelihood.

The initial hyperparameter’s set is Θ =

{1; 12; 60}. The initial magnitude σ

= 0.7 and ini-

tial noise variance σ

= 0.1 were also treated as hy-

perparameters and, therefore, optimized together with

the set Θ. As already discussed, the technique used

to optimize the hyperparameters is the algorithm de-

scribed in (Rasmussen and Williams, 2006).

6.2 Bidimensional Prediction Results

Fig. 6 shows a plot of the predicted values using

the optimized hyperparameters, where it can be seen

that the uncertainty of May’s prediction is quite high,

mainly because the tax collection proﬁle changed

drastically in the training data. This behavior con-

tradicts the linear increasing trend that were used to

model the covariance function, since the linear regres-

sion of this speciﬁc month shows a clear downtrend.

However, in spite of the uncertainty level, the predic-

tion of this month turned out to be precise.

Also, it can be noted that November was the only

month whose target value fell off the uncertainty pre-

dictive interval delimited in this section. In spite the

Figure 6: Plot of the Gaussian process prediction in blue,

target SPU data in red. The error bars corresponds to a con-

ﬁdence interval of two standard deviations with respect to

the predictive mean (around 95% of conﬁdence).

fact that the predicted value is larger than the last

year’s value for this month, the rate of growth from

2009 to 2010 could not be estimated by this model

based only on the information of the training data.

6.3 Prediction Comparison and Error

Metrics

The resulting prediction obtained in Subsection 6.2

will be evaluated by comparison with other predic-

tive techniques and analyzed by different error met-

rics between the target data and the predictive data.

The comparative evaluation will be made month-by-

month with two other predictive approaches, one us-

ing an artiﬁcial neural network and another using an

economical indicator. Also, an yearly comparison

will be made with the projected tax collection, a rev-

enue estimation made by the Brazilian federal gov-

ernment and published by SPU.

The approach proposed by (Serrano et al., 2012)

addressed the same problem, where an artiﬁcial neu-

ral network is used to predict the SPU tax collection

for the year of 2010. On the other hand, a pure ﬁ-

nancial approach consists of projecting the annual tax

collection of SPU by readjusting the previous year’s

collection by an economic indicator. In this case, the

chosen indicator to measure the inﬂation of the period

is the National Index of Consumer’s Prices (IPCA),

consolidated by the Brazilian Institute of Geography

and Statistics (IBGE). In 2009, the twelve month ac-

cumulated index was 4,31% (IBGE, 2013).

The error metrics used in this subsection aim to

evaluate the goodness of ﬁt between the predicted

and the testing data set for all the predictive ap-

proaches, using the normalized root mean squarred

error (NRMSE), the mean absolute relative error

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

(MARE), the coefﬁcient of determination (d) and the

coefﬁcient of efﬁciency (e). The descriptive formulas

of each metric is described in Appendix A.

All the predictive approaches, including the one

proposed in this work, have their prediction error cal-

culated with respect to the target data and the results

are resumed in Table 1.

Table 1: Performance comparison by several error metrics.

Error

Metric

Opt.

Value

Gaussian

Process

Art.

Neural

Network

Inﬂation

NRMSE 0 0, 44833 0, 46320 0, 56246

MARE 0 0, 14830 0, 31021 0, 23222

d 1 0, 82107 0, 89463 0, 92603

e 1 0, 78072 0, 7659 0, 67730

It is important to notice that the overall error in

the Gaussian process prediction showed in Table 1

is mainly concentrated in November. Removing this

month from the error measurements would lead to

NRMSE = 0, 22644, MARE = 0, 12524, d = 0, 94

and e = 0, 94359.

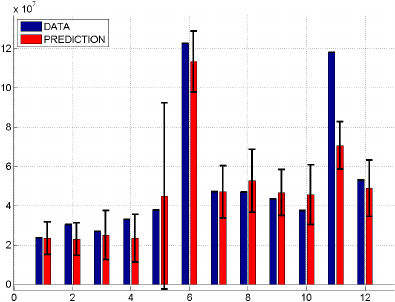
Fig. 7 shows a comparative plot among the target

data and all the predictive approaches side by side.

Finally, the Brazilian government revenue estima-

tion, published by SPU on its annual report (Secre-

taria de Patrimonio da Uni

ao (SPU), 2011), projects

an amount of tax collection by SPU in 2010 of

R$ 444, 085, 000.00, whereas the total amount col-

lected that year was R$ 635, 094, 000.00 - a gross dif-

ference of 38.48% between the estimated and the ex-

ecuted amount of tax collection.

The GPR approach presented in this work, in a

yearly basis, projected a total tax collection amount of

R$ 620, 703, 197.42, resulting in a gross difference of

2.27% between the projected and executed amounts.

6.4 Classiﬁcation Stage Proposals

The statistical description of the estimated variable,

natively given by Gaussian processes in the regres-

sion stage, can be used to build heuristics to classify a

predicted dataset into regular or possibly fraudulent.

Here, we propose two different heuristics that are suit-

able to fraud detection scenarios. However, given the

limited information publicly available from SPU re-

garding the dataset used in this work, the evaluation

of the proposed schemes is incomplete and deserve to

be better investigated in future studies.

The resulting regression obtained through GPR,

presented in Fig. 6, shows the variance of the esti-

mated variable as a measure of conﬁdence by trans-

lating it into error bars. Since this conﬁdence can be

as large or as small as we desire it to be, it is possible

to optimize a classiﬁcation stage based on this infor-

mation and, hence, build a trigger where high error

bars means high probability of fraud and vice versa.

In our case, without any doubt this system would clas-

sify May (month number 5) as a possibly fraudulent

one. Despite the high uncertainty level of the predic-

tion of this month, the prediction showed to be accu-

rate when compared to the target data.

Another classiﬁcation approach using the variance

information can be build simply by confronting the

predicted conﬁdence interval with the real data, when

it becomes available. In our case, this system would

classify November (month number 11) as a possibly

fraudulent one. SPU’s annual report (Secretaria de

Patrimonio da Uni

ao (SPU), 2011) states that an ex-

traordinary revenue of R$ 73, 759, 533.99 happened

in 2010, but it is not possible to precise in which

month it happened. In november, the difference be-

tween the predicted value and the actual revenue was

R$ 55, 015, 235.13.

Whereas the ﬁrst proposed system returns the

classiﬁed data in advance, together with the predicted

values in the regression stage, the second system

needs the real revenue data in order to classify it. On

the other hand, the second approach seeks for sam-

ples that are most dissimilar from the norm, whereas

the ﬁrst approach needs to be optimized in order to

learn the norm and distinguish anomalous behaviors.

As previously mentioned, it is not possible to eval-

uate the performance of these classiﬁcation stage pro-

posals due to the limited information regarding our

dataset, but the preliminary results using the statis-

tical description of the estimated variable showed in

this section encourages further studies on this topic.

7 CONCLUSIONS

This paper presented a GPR application, aimed to

model the intrinsic characteristics of a speciﬁc ﬁnan-

cial series. A unidimensional model for the GPR’s co-

variance function was proposed, and a pre-processing

stage reshaped the original data set based on its cross-

correlation proﬁle. That approach empowered the use

of a unidimensional GPR in a bidimensional environ-

ment by isolating high correlated months in one di-

mension and poor correlated months in another di-

mension.

Although Neural Networks are known for their

ﬂexibilities and reliable results when used for regres-

sion of time series, GPR are a transparent environ-

ment, with a parametric covariance function and no

Gaussian Process for Regression in Business Intelligence: A Fraud Detection Application

1 2 3 4 5 6 7 8 9 10 11 12

0.5

1.5

·10

Month

Target Data

GP Prediction

ANN Prediction

Financial Prediction

Figure 7: Monthly plot of target data and predictive results, in Reais (R$), indexed bu the t

month.

hidden layers, which can be an advantage when eval-

uating different components of a time series. The hy-

perparameters of GPR’s covariance function were op-

timized by maximum likelihood, i.e. the proposed

model let the data speaks for itself by learning the

hyperparameters only with information obtained from

the data. It is relevant to notice that the optimization

algorithm can converge to a local minimum, making

the initial choice of hyperparameters a critical part of

the optimization task.

Another positive point of GPR is related to the

complete statistical description of the predicted data,

which gives a powerful tool of conﬁdence. Using this

feature, a classiﬁcation method can be built to trig-

ger trusted and possibly fraudulent tax collection data

based on the conﬁdence interval of the prediction.

The regression results outperformed some classi-

cal predictive approaches such as ANN and econom-

ical indicator by several error metrics. In a yearly ba-

sis, the difference between the estimated and the real

tax collection for 2010 using the approach proposed

in this work was of 2.27%, whereas that difference

reached 38.48% with the Brazilian government own

estimation method.

The approach explored in this work showed to be

particularly useful for a small number of training sam-

ples, since the covariance function chosen to model

the series results in a strong relationship for closer

training points and a weak relationship for distant

points. On the other hand, adding more training years

before 2005 should not make a substantial difference

in the prediction result using this method.

ACKNOWLEDGEMENTS

The authors wish to thank the Spanish Government

(TEC 2012-38800-C03-02), the European Union

(FEDER), the Brazilian research, development and

innovation agencies FAPDF (TOA 193.000.555/

2015), CAPES (FORTE 23038.007604/2014-69) and

FINEP (RENASIC/PROTO 01.12.0555.00), as well

as the Brazilian Ministry of Planning, Budget and

Management, for their support to this work.

REFERENCES

Bernardo, J., Berger, J., Dawid, A., Smith, A., et al. (1998).

Regression and classiﬁcation using Gaussian process

priors. Bayesian statistics, 6:475.

Blum, M. and Riedmiller, M. (2013). Optimization of Gaus-

sian process hyperparameters using Rprop. In Euro-

pean Symposium on Artiﬁcial Neural Networks, Com-

putational Intelligence and Machine Learning.

Bolton, R. J. and Hand, D. J. (2002). Statistical fraud de-

tection: A review. Statistical Science, pages 235–249.

Cinlar, E. (2013). Introduction to stochastic processes.

Courier Dover Publications.

Davis, R. A. (2001). Gaussian process. In Brillinger, D.,

editor, Encyclopedia of Environmetrics, Section on

Stochastic Modeling and Environmental Change, NY.

Willey.

Dorronsoro, J. R., Ginel, F., S

anchez, C., and Cruz, C.

(1997). Neural fraud detection in credit card op-

erations. Neural Networks, IEEE Transactions on,

8(4):827–834.

IBGE (2013). Historical series of IPCA.

MacKay, D. J. (2003). Information theory, inference and

learning algorithms. Cambridge university press.

Murray-Smith, R. and Girard, A. (2001). Gaussian process

priors with ARMA noise models. In Irish Signals and

Systems Conference, pages 147–152. Maynooth.

Nagi, J., Yap, K., Tiong, S., Ahmed, S., and Mohammad,

A. (2008). Detection of abnormalities and electricity

theft using genetic support vector machines. In TEN-

CON 2008-2008 IEEE Region 10 Conference, pages

1–6. IEEE.

Orfanidis, S. J. (2007). Optimum signal processing: an in-

troduction. McGraw-Hill, New York, NY. ISBN 0-

979-37131-7.

erez-Cruz, F. and Bousquet, O. (2004). Kernel methods

and their potential use in signal processing. Signal

Processing Magazine, 21(3):57–65.

erez-Cruz, F., Van Vaerenbergh, S., Murillo-Fuentes, J. J.,

azaro-Gredilla, M., and Santamaria, I. (2013). Gaus-

sian processes for nonlinear signal processing. IEEE

Signal Processing Magazine, 30(4):40–50.

KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing

Rasmussen, C. E. and Williams, C. K. I. (2006). Gaus-

sian Processes for Machine Learning. The MIT Press,

Cambridge, MA. ISBN 0-262-18253-X.

Robertson, D. (2013). Global card fraud losses reach $11.27

billion in 2012. Nilson Report, The, (1023):6.

Secretaria de Patrimonio da Uni

ao (SPU) (2011). Relat

orio

de gest

ao 2010.

Serrano, A. M. R., da Costa, J. P. C. L., Cardonha, C. H.,

Fernandes, A. A., and de Sousa Jr., R. T. (2012). Neu-

ral network predictor for fraud detection: A study case

for the federal patrimony department. In Proceed-

ing of the Seventh International Conference on Foren-

sic Computer Science (ICoFCS) 2012, pages 61–66,

Bras

ılia, Brazil. ABEAT. ISBN 978-85-65069-08-3.

Snoek, J., Larochelle, H., and Adams, R. P. (2012). Prac-

tical bayesian optimization of machine learning algo-

rithms. In NIPS, pages 2960–2968.

Williams, C. K. and Barber, D. (1998). Bayesian clas-

siﬁcation with Gaussian processes. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

20(12):1342–1351.

Williams, C. K. and Rasmussen, C. E. (1996). Gaussian

processes for regression.

A ERROR METRIC FORMULAS

Being t ∈ R

a target vector with the desired values

and y ∈ R

an output vector of a regression model,

the goodness of ﬁt between t and y will be ginve in

terms of:

1. Normalized Root Mean Squared Error (NRMSE):

i=1

− y

)

Var[t]

2. Mean Absolute Relative Error (MARE):

i=1



− y



3. Coefﬁcient of Determination (d):

i=1

−

t)(y

−

i=1

−

i=1

−

4. Coefﬁcient of Efﬁciency (e):

1 −

i=1

− y

)

i=1

−

Gaussian Process for Regression in Business Intelligence: A Fraud Detection Application