Perceptron Learning for Classification Problems
Impact of Cost-Sensitivity and Outliers Robustness
Philippe Thomas
Université de Lorraine, CRAN, UMR 7039, Campus Sciences, BP 70239, 54506 Vandœuvre-lès-Nancy cedex, France
CNRS, CRAN, UMR7039, France
Keywords: Cost-Sensitive Approach, Multilayer Perceptron, Outliers, Robustness, Levenberg-Marquardt, Label Noise.
Abstract: In learning approaches for classification problem, the misclassification error types may have different
impacts. To take into account this notion of misclassification cost, cost sensitive learning algorithms have
been proposed, in particular for the learning of multilayer perceptron. Moreover, data are often corrupted
with outliers and in particular with label noise. To respond to this problem, robust criteria have been
proposed to reduce the impact of these outliers on the accuracy of the classifier. This paper proposes to
associate a cost sensitivity weight to a robust learning rule in order to take into account simultaneously these
two problems. The proposed learning rule is tested and compared on a simulation example. The impact of
the presence or absence of outliers is investigated. The influence of the costs is also studied. The results
show that the using of conjoint cost sensitivity weight and robust criterion allows to improve the classifier
accuracy.
1 INTRODUCTION
Learning approaches have been extensively used for
knowledge Discovery in Data problems, in general,
and more particularly in classification problems.
Different tools may be used to design classifiers
including logic based algorithms (decision trees, rule
based classifiers…) statistical learning algorithms
(naïve Bayes classifiers, Bayesian network…)
instance approaches (k-nearest neighbours) support
vector machine and neural networks (multilayer
perceptron, radial basis function networks)
(Kotsiantis, 2007).
This paper focuses on multilayer perceptron
(MLP) which is able to approach different classifiers
of diverse complexity: Euclidian distance,
regularized and standard Fisher, robust minimal
empirical error, and maximum margin (support
vectors) (Raudys and Raudys, 2010).
With the goal of classification of data into
different classes comes the notion of
misclassification cost. The problem of cost-
sensitivity in learning classification applications has
received important attention during the last years
(Geibel et al., 2004; Raudys and Raudys, 2010;
Castro and Braga, 2013).
The main goal of classifier construction by using
learning approach is to minimize the mean square of
the error on a training data set. However, the
misclassification of a pattern in one class may not
have the same impact that another misclassification
of another pattern in another class. As example in
medical diagnosis, the cost of non-detection (false
negative) and of false alarm (false positive) don’t
have the same impact on the patient live, and so
don’t have the same cost.
Moreover, in case of an imbalanced training set,
such approaches may lead to models which are
biased toward the overrepresented class (Castro and
Braga, 2013), and in many cases (quality
monitoring, medical diagnosis, credit risk
prediction…) the overrepresented class is often the
less important one (Zadrozny et al., 2003).
To take into account this problem different cost-
sensitive approaches have been proposed. Zadrozny
et al., (2003) classified these approaches in three
main classes:
Making particular classifier learners cost-
sensitive (Drummond and Holte 2000, Garcia
et al. 2013; Castro and Braga, 2013),
Using Bayes risk theory to assign each
example to its lower risk class (Domingos
106
Thomas, P..
Perceptron Learning for Classification Problems - Impact of Cost-Sensitivity and Outliers Robustness.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 3: NCTA, pages 106-113
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
1999; Margineantu, 2002; Zadrozny and
Elkan, 2001),
Using of meta-models for converting
classification learning dataset into cost-
sensitive ones (Domingos, 1999; Fan et al.,
1999; Zadrozny et al., 2003).
This work is relevant to the first category
because its aim is to propose a cost-sensitive
learning algorithm for multilayer perceptron. A
misclassification cost is introduced in the criterion to
minimize in order to take into account cost
sensitivity during learning.
Cost sensitivity problem in classifier design is
not the only one to be addressed. The problem to the
corruption of data by outliers may lead to biased
models.
Different outlier definitions has been proposed in
the literature (Hawkins 1980, Barnett and Lewis
1994, Moore and McCabe 1999…). All of them are
accordingly to say that outlier is a different data than
the other data of the complete dataset (Cateni et al.
2008). In classification problem, outliers may be the
consequence of two types of noise (Zhu and Wu
2004):
Attribute noise (addition of a small Gaussian
noise to each attribute during data collection),
Class noise (modification of the label
assigned to the pattern).
Different studies have shown that class noise has a
greater impact on the model design (Zhu and Wu
2004, Sàez et al. 2014). Frénay and Verleysen
(2014) have performed a review of classification
approaches in presence of label noise. They have
proposed to classify these approaches into three
classes:
Label-noise robust approaches (Manwani and
Sastry 2013)
Label noise cleansing approaches (Sun et al.
2007)
Label noise tolerant approaches (Swartz et al.
2004).
The considered approach is more related to the
first one. Classically, the learning algorithm is based
on the use of the classical ordinary least-squares
criterion (L2 norm) also called Mean Squared Error
(MSE). To limit the impact of outliers on the
resulting model, an M-estimator is used which is
initially developed in robust statistics but was
introduced for neural network learning by many
authors (Chen and Jain 1991, Bloch et al. 1994,
1997, Liano 1996). It can be noticed that, contrary to
popular belief, neural network are not intrinsically
robust to outliers (Thomas et al. 1999).
The main goal of this paper is to associate a cost-
sensitivity weight and robust norm in the criterion to
minimize in order to derive the learning algorithm of
MLP for classification problem.
In the next part, the structure of the considered
MLP is recalled and the proposed learning algorithm
presented. In part 3, the simulation example used to
test the proposed algorithm is presented and the
results obtained are shown and discussed before to
conclude.
2 MULTILAYER PERCEPTRON
2.1 Structure
Multilayer neural network including only one hidden
layer (using a sigmoidal activation function) and an
output layer is able to approximate all nonlinear
functions with the desired accuracy (Cybenko 1989,
Funahashi 1989). For a seak of simplicity of
presentation, only the single output case is
considered here, the multi outputs case may easily
derivated from this case. The structure of such MLP
is given by:
2 1 1
11
ˆ
..
oi
nn
o h h hi i h
hi
y g w g w x b b
(1)
where
i
x
are the n
i
inputs,
1
hi
w
are connecting
weights between input and hidden layers,
1
h
b
are the
hidden neurons biases, g
h
(.) is the activation function
of the hidden neurons (hyperbolic tangent),
2
h
w
are
connecting weights between hidden and output
layers, b is the bias of the output neuron, g
o
(.) is the
activation function of the output neuron, and
ˆ
y
is
the network output.
Due to the fact that the considered problem is a
classification one, g
o
(.) is chosen as a sigmoidal
function.
Due to the fact that learning of a MLP is
performed by using a local search of minimum, the
choice of the initial parameters set is crucial for the
model accuracy. Different initialization algorithms
have been proposed in the past (Thomas and Bloch
1997). A modification of the Nguyen and Widrow
(NW) algorithm (Nguyen and Widrow 1990) is used
here, which allows a random initialization of
weights and biases to be associated with an optimal
placement in the input space (Demuth and Beale
1994).
Perceptron Learning for Classification Problems - Impact of Cost-Sensitivity and Outliers Robustness
107

2.2 Learning Algorithm
The main goal for the learning algorithm in
classifaction problem is to design a model able to
associate the good class to each pattern. This model
is directly extracted from a learning dataset. To do
that, the mean root square error performed between
the predicted output of the model and the real
desired one must be minimized. So the classical
quadratic criterion to minimize is:
2
1
1
( ) ( , )
2
n
k
Vk
n
(2)
where
comprises all the unknown network
parameters (weights and biases), n is the size of the
learning dataset and
is the prediction error given
by:
ˆ
( , ) ( ) ( , )k y k y k
(3)
where y(k) is the real desired class of the pattern k
and
ˆ
( , )yk
is the predicted one by the network.
Such criterion to minimize is not able to take into
account the fact that learning dataset may be
polluted by outliers or the fact that the cost
associated to each type of missclassification error
may be different. To do that two weights may be
introduced into the criterion in order to take into
account these facts.
To take into account the presence of outliers in
the dataset, a robust criterion to minimize is used. It
is based on a robust identification method proposed
by Puthenpura and Sinha (1990), itself derived from
the Huber’s model of measurement noise
contamined by outliers (Huber 1964) which
assimilates the noise distribution e to a mixture of
two Gaussian density functions of mean 0 and
variance
2
1
for the first Gaussian which represents
the normal noise distribution and variance
2
2
for
the second Gaussian which represents the outliers
distribution such that
22
12
:
22
12
~ (1 ) (0, ) (0, )e N N
(4)
where
is the large error occurence probabily.
Generally, the probabilty
and the two variances
2
1
and
2
2
are unknow and must be estimated. To
do that, the preceding model (4) is replaced by:
22
12
( , ) ~ (1 ( )) (0, ) ( ) (0, )k k N k N
(5)
where
( ) 0k
when
( , )kM
and
( ) 1k
otherwise. M is a bound which is taken equal to
1
3
(Aström, 1980). The estimations of variance
2
1
and
2
2
are calculated at each iteration i and are given by
(Ljung 1987):
1
21
()
0.7
( ) 3. ( )
MAD
i
ii
(6)
where MAD is the median of
( , )k
with
as the median of
( , )k
.
This definition of the prediction error of the
network allows to define the robust criterion to
minimize:
2
2
1
1 ( , )
()
2
()
n
k
k
V
n
k
(7)
Where
2
()k
is the robust weight (estimated
variance) associated to the predicted error of the k
th
pattern:
2 2 2
12
ˆˆ
( ) (1 ( )) ( ) ( ) ( )k k i k i
(8)
To divide the predicted error by its variance
allows to limit the impact of too large errors on the
learning processus. Moreover, the use of such
criterion gives a regularization effect on the learning
(Thomas et al. 1999).
This criterion to minimize is able to take into
account the presence of outliers in the dataset. To
take into account the different costs of the different
missclassification types, a second weight (Castro
and Braga 2013) must be included in this criterion
(7) which becomes:
2
2
1
1 ( , )
( ) ( ).
2
()
n
ost
k
k
V C k
n
k
(9)
Where C
ost
(k) is the misclassification cost of the
predicted error for the k
th
pattern which is given by
table 1.
Table 1: Cost of misclassification.
Class 0 Class1
Class 0
C
00
C
01
Class 1
C
10
C
11
real
class
predicted class
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
108

The 2
nd
order Taylor series expansion of the
criterion to minimize (9) leads to the classical
Gauss-Newton algorithm:
1 1 '
ˆ ˆ ˆ ˆ
( ( )) ( )
i i i i
HV
(10)
where
ˆ
i
is the set of network parameters estimated
at iteration i,
'
ˆ
()
i
V
is the gradient of the criterion
given by:
'
2
1
1 ( , )
( ) ( , ). ( ).
()
n
ost
k
k
V k C k
n
k
(11)
where
( , )k
is the gradient of
ˆ
( , )yk
with
respect to
.
ˆ
()
i
H
is the Hessian matrix which can be
estimated by using the Levenberg-Marquardt update
rule:
"
1
1
( ) ( , ) ( ( , )) ( , )
n
T
k
H k L k k I
n
(12)
where I is the identity matrix and
a small non
negative scalar which must be adapted during the
learning process.
3 SIMULATION EXAMPLE
3.1 Simulation Example
To illustrate the proposed learning algorithm, a
simple simulation example is used; it is derived from
the example proposed by Lin et al. (2000). This
example considers a population consisting of two
subpopulations. The positive subpopulation follows
a bivariate normal distribution with mean (0, 0)
T
and
covariance matrix diag(1, 1), whereas the negative
subpopulation follows two bivariate normal
distributions with mean (2, 2)
T
with covariance
diag(2, 1) for the first subpopulation and with mean
(-2, -2)
T
with covariance diag(2, 1) for the second
subpopulation. The population is unbalanced: The
positive and negative subpopulations account for
80% and 20% of the total population, respectively.
The negative subpopulation is balanced and follows
two different laws in order to ensure that the two
classes cannot be linearly separable.
Figure 1 shows the repartition of the two classes
in the space of the two inputs. The red circles
represent the class0, when the blue triangles
represent the class1. It can be noticed that these two
classes are partially confused. This fact implies that
even the best classifier is not able to perform its task
without generatingmisclassification.
Figure 1: Distribution of the two classes.
3.2 Experimental Protocol
In the first step, a dataset comprising 2000 patterns
is constructed which follows the distribution
described above. This dataset is split into two
datasets of 1000 patterns each, one for the learning
and the other for the validation. A classifier is
designed using a MLP with 2 inputs and 10 hidden
neurons which appears sufficient to learn the model.
The main goal of classifers is to reduce the
number of misclassified patters. The classical
criterion used to evaluate classifiers is the
misclassification rate (error rate or “zero-one” score
function (Hand et al., 2001):
01
1
1
( ), ( , )
n
k
S I y k y k
n
(13)
where
,1I a b
when
ab
and 0 otherwise.
Two others indicators must be determined, the false
alarm rate (FA) and the non-detection rate (ND):
FP
FA
FP TN
FN
ND
FN TP
(14)
where FP stands for the number of false positives,
TN for the number of true negatives, FN the number
of false negatives, and TP the number of true
positives.
The last indicator used takes into account the
costs of misclassification defined Table 1 and is
given by:
01 10
..Cost C FP C FN
(15)
In order to evaluate the impact of the proposed
approach, two experiments are performed. The first
one learns a MLP classifier on a dataset free of
-8 -6 -4 -2 0 2 4 6
-6
-4
-2
0
2
4
6
Perceptron Learning for Classification Problems - Impact of Cost-Sensitivity and Outliers Robustness
109
outliers when the second one uses a dataset where
10% of data in the learning dataset are noise label
(switching of the label of the considered pattern).
Four learning algorithms are tested and compared:
- Levenberg-Marquardt (LM) without cost
weight and without robust criterion,
- LM without cost weight and with robust
criterion (LMR),
- LM with cost weight and without robust
criterion (LMC),
- LM with cost weight and with robust
criterion (LMRC).
To evaluate the impact of choice of the
misclassification costs, two cost matrices have been
used given by tables 2 and 3.
Table 2: Cost of misclassification 2-5.
Table 3: Cost of misclassification 2-10.
3.3 Results on Outliers Free Dataset
The table 4 gives the results obtained with the four
learning algorihtms on the outliers free dataset with
the two types of costs.
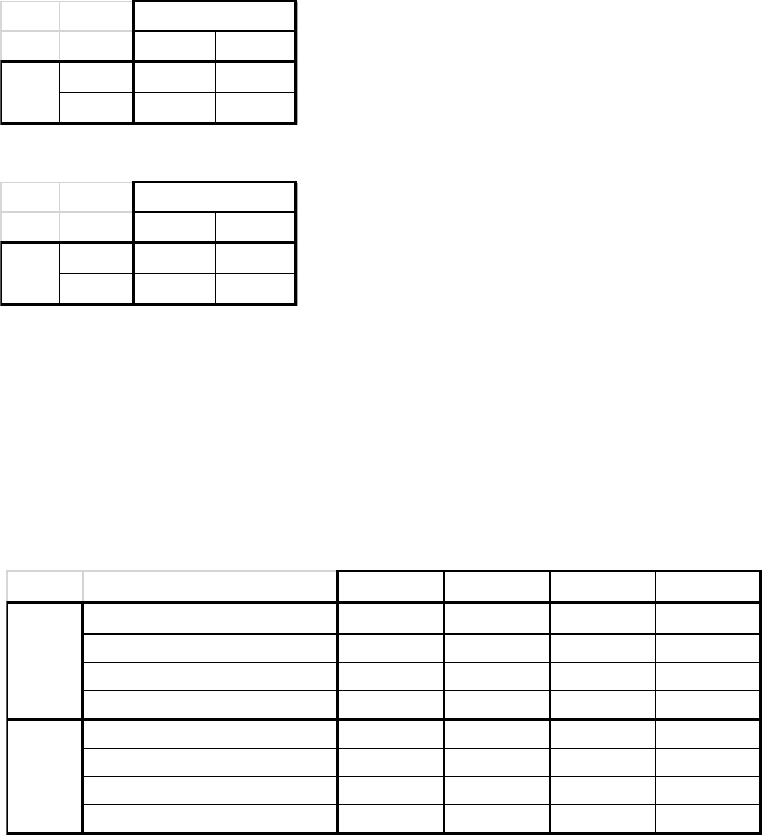
By studying these results, the first remark we can
do is, that the using of the weight cost tends to
improve the ND rate at the expense of the FA rate.
As example, the using of a cost 2-5 in the LM
algorithm improves the ND rate of 29% when the
cost 2-10 leads to an improvement of 40%. In the
same time the FA rate is degraded of 12% in the first
case and of 58% in the second one.
In the same time, even in absence of label noise,
the robust learning rule allows to improve the results
both for FA rate (12%) and ND rate (17%)
comparing to the classical LM algorithm. This fact is
due to the regularisation effect of the robust criterion
and of the fact that the two classes are partially
confused.
The conjoint use of cost sensitive weight and
robust criterion slightly deteriorates the results
obtained with the cost 2-5. This degradation is of 4%
for the FA rate and of 3% for the ND rate. It can be
noticed that with the cost 2-10, this approach
deteriorates slightly the FA rate (22%) but for an
improvement of the ND rate (26%). So, in absence
of label noise, the conjoint use of weight sensitive
cost and robust criterion gives equivalent results
than the use of weight sensitive cost alone. These
results are confirmed when the Cost values are
studied. For the cost 2-5, the using of robust
criterion alone, weigth sensitive alone or both give
equivalent results when for the cost 2-10, the using
of both robust criterion and cost-sensitive weight
gives the best results.
3.4 Results on Outliers Polluted Dataset
In a second step, the learning dataset is corrupted by
10% of noise label. The same algorithms are used
and the results obtained are presented table 5. When
the misclassification rate S
01
obtained whith the
outliers free learning dataset and the corrupted
dataset, are compared, it can be noticed that only the
classical LM algorithm without cost sensitive weight
Table 4: Results obtained on the outliers free dataset.
Class 0 Class1
Class 0 1 2
Class 1 5 1
predicted class
real
class
Class 0 Class1
Class 0 1 2
Class 1 10 1
real
class
predicted class
Cost
S
01
FA rate ND rate
Without Robust Without Cost 346 9.50% 5.40% 25.49%
With Robust Without Cost 291 8.10% 4.77% 21.08%
Without Robust With Cost 281 8.50% 6.03% 18.14%
With Robust With Cost 290 8.80% 6.28% 18.63%
Without Robust Without Cost 606 9.50% 5.40% 25.49%
With Robust Without Cost 506 8.10% 4.77% 21.08%
Without Robust With Cost 446 9.90% 8.54% 15.20%
With Robust With Cost 396 10.60% 10.43% 11.27%
Cost
01
= 2
Cost
10
= 5
Cost
01
= 2
Cost
10
= 10
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
110

Table 5: Results obtained on the outliers corrupted dataset.
Figure 2: Classes bounds obtained on the outliers polluted dataset. LM in magenta - LM robust in black – LM cost sensitive
in red – LM robust cost sensitive in green.
and robust criterion sees its accuracy slightly
degraded (4%).
However, by studying the ND rates, this rate is
deteriorate when no robust criterion is used up to
49% when the cost 2-5 is used with the LM
algorithm with cost without robust. On the contrary,
this ND rate remains more stable when robust
criterion is used with even an improvement of 4%
with the LM algorithm with cost weight and robust
criterion for cost 2-10. The using of robust criterion
associated to cost sensitive weight improves the ND
rate comparing to those obtained with the cost –
sensitive weight alone (improvement of 20% for cost
2-5 and of 41% for cost 2-10).
When the Cost values are studied the conjoint
use of cost sensitive weight and robust criterion
allows to maintain the results accuracy even in
presence of noise label.
The figure 2 presents the bounds obtained on the
outliers polluted learning dataset. This figure
shows that classical LM algorithm gives bounds
very tortuous comparing to those obtained with other
appraoches. This fact shows that robust criterion as
cost sensitive weight approaches have both a
regularisation effect on the learning process. This
figure shows also that the using of a cost sensitive
weight (with or without robust criterion) favoures
the class 1 over the class 0.
4 CONCLUSIONS
This paper deals with the problem of
misclassification cost in learning of MLP classifiers.
It studies the impact of outliers on the classifier
accuracy and proposes to associate a cost sensitive
weight (to take into account the different cost of
misclassification) to a robust criterion (to avoid the
Cost
S
01
FA rate ND rate
Without Robust Without Cost 381 9.90% 4.77% 29.90%
With Robust Without Cost 305 8.20% 4.40% 23.40%
Without Robust With Cost 333 8.40% 3.64% 26.96%
With Robust With Cost 310 8.90% 5.65% 21.57%
Without Robust Without Cost 686 9.90% 4.77% 29.90%
With Robust Without Cost 540 8.20% 4.40% 23.40%
Without Robust With Cost 482 9.30% 7.04% 18.14%
With Robust With Cost 384 10.40% 10.30% 10.78%
Cost
01
= 2
Cost
10
= 5
Cost
01
= 2
Cost
10
= 10
-6 -4 -2 0 2 4 6 8
-4
-3
-2
-1
0
1
2
3
4
5
Perceptron Learning for Classification Problems - Impact of Cost-Sensitivity and Outliers Robustness
111
impact of outliers on classifier accuracy) in a
classical Levenberg-Marquadt learning algorithm.
The proposed learning algorithm is tested and
compared with three other ones on a simulation
example. The impact of the choice of
misclassification costs and of the presence of
outliers is investigated. The results show that the
conjoint use of cost-sensitive weight and robust
criterion improves the classifier accuracy.
In our future works, this approach will be tested
on other benchmark datasets in order to confirm the
results. The impact of imbalanced repartition in the
dataset will be also investigated. Last this approach
will be extended to the multiclass case.
REFERENCES
Aström, K.J., 1980. Maximum likelihood and prediction
error methods. Automatica, 16, 551-574.
Bloch G., Theilliol D., Thomas P., 1994. Robust
identification of non linear SISO systems with neural
networks. System Identification (SYSID'94), a
Postprint Volume from the IFAC Symp., Copenhagen,
Denmark, July 4-6, M. Blanke, T. Söderström (Eds.),
Pergamon, 1995, Vol. 3, pp. 1417-1422.
Bloch G., Thomas P., Theilliol D., 1997. Accommodation
to outliers in identification of non linear SISO systems
with neural networks. Neurocomputing, 14, 85-99.
Barnett V. Lewis T., 1994, Outliers in statistical data,
John Wiley, ISBN 0-471-93094-6, Chichester.
Castro C.L., Braga A.P., 2013. Novel cost-sensitivity
approach to improve the multilayer perceptron
performance on imbalanced data. IEEE Trans. On
Neural Networks and Learning Systems, 24, 6, 888-
899.
Cateni S., Colla V., Vannucci M., 2008. Outlier Detection
Methods for Industrial Applications, Advances in
Robotics, Automation and Control, Jesus Aramburo
and Antonio Ramirez Trevino (Ed.), ISBN: 978-953-
7619-16-9, InTech, Available from:
http://www.intechopen.com/books/advances_in_roboti
cs_automation_and_control/outlier_detection_method
s_for_industrial_applications
Chen D.S., Jain R.C., 1991. A robust back propagation
learning algorithm for function approximation. Proc.
Third Int. Workshop on Artificial Intelligence and
Statistics, Fort Lauderdale, FL, 218-239.
Cybenko G., 1989. Approximation by superposition of a
sigmoïdal function. Math. Control Systems Signals 2,
303-314.
Demuth H., Beale P. 1994. Neural networks toolbox user's
guide V2.0. The MathWorks, Inc.
Domingos P., 1999. MetaCost: A general method for
making classifiers cost sensitive. Proc. of the 5
th
Int.
Conf. on Knowledge Discovery and Data Mining, 78-
150.
Drummond C., Holte R.C., 2000. Exploiting the cost
(in)sensitivity of decision tree splitting criteria. Proc.
of the 17
th
Int. Conf. on Machine Learning, 239-246.
Fan W., Stolfo S.J., Zhang J., Chan P.K., 1999. AdaCost:
Misclassification cost-sensitive boosting. Proc. of Int.
Conf. on Machine Learning, pp. 97-105.
Frénay B., Verleysen M., 2014. Classification in the
presence of label noise: a survey. IEEE trans. On
Neural Networks and Learning Systems, 25, 845-869.
Funahashi K., 1989. On the approximate realisation of
continuous mapping by neural networks. Neural
Networks 2, 183-192.
Garcia R.A.V., Marqués A.I., Sanchez J.S., Antonio-
Velasquez J.A., 2013. Making accurate credit risk
predictions with cost-sensitive MLP neural networks
in Management Intelligent Systems, Advances in
Intelligent Systems and Computing, 220, 1-8.
Geibel, Peter, Brefeld, Ulf, and Wysotzki, Fritz.
Perceptron and svm learning with generalized cost
models. Intelligent Data Analysis, 8:439–455, 2004
Hand, D, Mannila, H., Smyth, P., 2001. Principles of data
mining. The MIT press, Cambridge
Hawkins, D., 1980. Identification of Outliers, Chapman
and Hall, London.
Huber P.J., 1964. Robust estimation of a location
parameter. Ann. Math. Stat., 35, 73-101.
Kotsiantis, S.B., 2007. Supervised machine learning: a
review of classification techniques. Informatica, 31,
249–268.
Liano K., 1996. Robust error for supervised neural
network learning with outliers. IEEE Trans. on Neural
Networks, 7, 246-250.
Lin Y., Lee Y., Wahba G., 2000. Support vector machines
for classification in nonstandard situations. Technical
Repport,
http://roma.stat.wisc.edu/sites/default/files/tr1016.pdf.
Ljung L., 1987. System identification: theory for the user.
Prentice-Hall, Englewood Cliffs.
Manwani N., Sastry P.S. 2013. Noise tolerance under risk
minimization. IEEE Trans. Cybern., 43, 1146–1151.
Margineantu D., 2002. Class probability estimation and
cost-sensitive classification decision. Proc. of the 13
th
European Conference on Machine Learning, 270-281.
Moore D.S., McCabe G.P., 1999. Introduction to the
Practice of Statistics. Freeman & Company.
Nguyen D., Widrow B., 1990. Improving the learning
speed of 2-layer neural networks by choosing initial
values of the adaptive weights. Proc. of the Int. J.
Conf. on Neural Networks IJCNN'90, 3, 21-26.
Puthenpura S., Sinha N.K., 1990. A robust recursive
identification method. Control-Theory and Advanced
Technology 6: 683-695.
Raudys S., Raudis A., 2010. Pairwise costs in multiclass
perceptrons. IEEE Tans. On Pattern Analysis and
Machine Intelligence, 32, 7, 1324-1328.
Sàez J., Galar M., Luengo J., Herrera F. 2014. Analyzing
the presence of noise in multi-class problems:
Alleviating its influence with the one-vs-one
decomposition, Knowl. and Information Systems, 38,
179–206.
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
112
Sun J.W., Zhao F.Y., Wang C.J., Chen S.F., 2007.
Identifying and correcting mislabeled training
instances. Proc. Future Generat. Commun. Netw., 1,
Jeju-Island, South Korea, 244–250.
Swartz T., Haitovsky Y., Vexler A., Yang T., 2004.
Bayesian identifiability and misclassification in
multinomial data, Can. J. Statist., 32, 285–302.
Thomas P., Bloch G., 1997. Initialization of one hidden
layer feed-forward neural networks for non-linear
system identification. Proc. of the 15th IMACS World
Congress on Scientific Computation, Modelling and
Applied Mathematics WC’97 295–300.
Thomas P., Bloch G., Sirou F., Eustache V., 1999. Neural
modeling of an induction furnace using robust learning
criteria. J. Integrated Computer Aided Engineering, 6,
1, 5–23.
Zadrozny B., Elkan C., 2001. Learning and making
decisions when costs and probabilities are both
unknown. Proc. of the 7
th
Int. Conf. on Knowledge
Discovery and Data Mining, 203-213.
Zadrozny B., Langford J., Abe N., 2003. 3
rd
IEEE
International Conference on Data Mining, 19-22
November, 435-442.
Zhu X., Wu X., 2004. Class noise vs. attribute noise: A
quantitative study. Artif. Intell. Rev., 22, 177–210.
Perceptron Learning for Classification Problems - Impact of Cost-Sensitivity and Outliers Robustness
113
