A Yet Faster Version of Complex-valued Multilayer Perceptron Learning
using Singular Regions and Search Pruning
Seiya Satoh and Ryohei Nakano
Department of Computer Science, Chubu University, 1200 Matsumoto-cho, Kasugai 487-8501, Japan
Keywords:
Complex-valued Multilayer Perceptron, Learning Method, Singular Region, Search Pruning.
Abstract:
In the search space of a complex-valued multilayer perceptron having J hidden units, C-MLP(J), there are
singular regions, where the gradient is zero. Although singular regions cause serious stagnation of learning,
there exist narrow descending paths from the regions. Based on this observation, a completely new learning
method called C-SSF (complex singularity stairs following) 1.0 was proposed, which utilizes singular regions
to generate starting points of C-MLP(J) search. Although C-SSF1.0 finds excellent solutions of successive
C-MLPs, it takes long CPU time because the number of searches increases as J gets larger. To deal with this
problem, C-SSF1.1 was proposed, a few times faster by the introduction of search pruning, but it still remained
unsatisfactory. In this paper we propose a yet faster C-SSF1.3, going further with search pruning, and then
evaluate the method in terms of solution quality and processing time.
1 INTRODUCTION
Complex-valued neural networks (Hirose, 2012) have
the attractive features real-valued ones don’t have. A
complex-valued multilayer perceptron (C-MLP) can
naturally represent a periodic and/or unbounded func-
tion, which is not easy at all for a real-valued MLP.
Among learning methods of C-MLPs, complex
back propagation (C-BP) (Kim and Guest, 1990; Le-
ung and Haykin, 1991) is basic and well-known.
A higher-order learning method was proposed to
get better performance (Amin et al., 2011). Com-
plex Broyden-Fletcher-Goldfarb-Shanno (C-BFGS)
(Suzumura and Nakano, 2013) finds nice solutions af-
ter many independent runs.
There exist flat subspaces called singular regions
in the C-MLP search space (Nitta, 2013), as is the
case with a real-valued MLP (Fukumizu and Amari,
2000). Singular regions have been avoided (Amari,
1998) because they cause serious stagnation of learn-
ing. However, they can be utilized as excellent initial
points when we perform search for successive num-
bers of hidden units. This viewpoint led to the in-
vention of a completely new learning method. Ac-
tually, a method called SSF (Singularity Stairs Fol-
lowing) (Satoh and Nakano, 2013) was proposed
for real-valued MLPs, utilizing reducibility mapping
(Fukumizu and Amari, 2000) and eigenvector descent
(Satoh and Nakano, 2012). It stably and successively
found excellent solutions.
Recently a complex version of SSF, called C-SSF
1.0, was proposed (Satoh and Nakano, 2014), uti-
lizing complex reducibility mapping (Nitta, 2004),
eigenvector descent, and C-BFGS. It stably found ex-
cellent solutions in C-MLP search space, whose so-
lution quality was better than C-BFGS. However, it
took several times longer than C-BFGS. To make C-
SSF1.0 faster, C-SSF1.1 (Satoh and Nakano, 2015)
was proposed by introducing search pruning. It ran a
few times faster than C-SSF1.0 without losing the su-
perb solution quality, but still remained unsatisfactory
in processing time.
This paper proposes a yet faster version of C-SSF
called C-SSF1.3 by introducing two contrivances:
putting a ceiling on the number of searches and utiliz-
ing multiple best solutions to generate starting points.
Our experiments compare solution quality and pro-
cessing time of the proposed C-SSF1.3 with those of
C-SSF1.1, C-BP, and C-BFGS.
2 SINGULAR REGIONS
This section explains how singular regions are gener-
ated. Consider a complex-valued MLP with J hidden
units, C-MLP(J), whose output is f
J
.
122
Satoh, S. and Nakano, R..
A Yet Faster Version of Complex-valued Multilayer Perceptron Learning using Singular Regions and Search Pruning.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 3: NCTA, pages 122-129
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

f
J
(x;θ
J
) = w
0
+
J
∑
j=1
w
j
z
j
, z
j
≡ g(w
T
j
x) (1)
Here θ
J
= {w
0
,w
j
,w
j
, j = 1,··· , J} is a parameter
vector. Input x, weights w
j
, w
j
, output f
J
, and teacher
signal y are all complex. Given data {(x
µ
,y
µ
),µ =
1,··· ,N}, we want to find θ
J
minimizing the follow-
ing.
E
J
=
N
∑
µ=1
δ
µ
δ
µ
, δ
µ
≡ f
J
(x
µ
;θ
J
) − y
µ
(2)
Next, consider C-MLP(J−1) with J−1 hidden units.
Its output is f
J−1
.
f
J−1
(x;θ
J−1
) = u
0
+
J−1
∑
j=1
u
j
v
j
, v
j
≡ g(u
T
j
x) (3)
Here θ
J−1
= {u
0
,u
j
,u
j
, j = 1,··· ,J − 1} is a param-
eter vector of C-MLP(J−1), and let the optimal θ
J−1
be
b
θ
J−1
.
Sussmann (Sussmann, 1992) pointed out the
uniqueness and reducibility of real-valued MLPs.
Much the same uniqueness and reducibility hold for
complex-valued MLPs (Nitta, 2004). Now consider
three reducibility mappings α, β, and γ; then, apply
α, β, and γ to the optimal
b
θ
J−1
to get
b
Θ
α
J
,
b
Θ
β
J
, and
b
Θ
γ
J
respectively.
b
θ
J−1
α
−→
b
Θ
α
J
,
b
θ
J−1
β
−→
b
Θ
β
J
,
b
θ
J−1
γ
−→
b
Θ
γ
J
b
Θ
α
J
≡ {θ
J
|w
0
= bu
0
, w
1
=0,
w
j
= bu
j−1
,w
j
=bu
j−1
, j=2,··· ,J} (4)
b
Θ
β
J
≡ {θ
J
|w
0
+w
1
g(w
10
)= bu
0
,
w
1
=[w
10
,0,··· ,0]
T
,w
j
= bu
j−1
,
w
j
= bu
j−1
, j=2,··· ,J} (5)
b
Θ
γ
J
≡ {θ
J
|w
0
= bu
0
,w
1
+w
m
= bu
m−1
,
w
1
=w
m
=bu
m−1
,w
j
= bu
j−1
,
w
j
=bu
j−1
, j∈{2,··· ,J}\{m}} (6)
Now, we have the following singular regions.
(1) The intersection of
b
Θ
α
J
and
b
Θ
β
J
forms singular re-
gion
b
Θ
αβ
J
, where only w
10
is free. In the singular re-
gion the following hold:
w
0
= bu
0
, w
1
= 0, w
1
= [w
10
,0,··· ,0]
T
,
w
j
= bu
j−1
, w
j
= bu
j−1
, j = 2,··· ,J.
(2)
b
Θ
γ
J
is a singular region, where the following
holds: w
1
+ w
m
= bu
m−1
, m=2, · · · ,J.
After finishing learning of C-MLP(J−1), C-SSF
starts learning of C-MLP(J) from points in the sin-
gular region of C-MLP(J). Since the gradient is zero
all over the singular region, the gradient won’t give
us any information in which direction to go. Thus
we employ eigenvector descent (Satoh and Nakano,
2012). Picking up a negative eigenvalue, we have two
search directions based on its eigenvector.
3 C-SSF
This section describes the former versions and the
proposed version of C-SSF (Complex Singularity
Stairs Following). C-SSF learns C-MLPs.
3.1 Basic Framework
The origin of C-SSF is C-SSF1.0 (Satoh and Nakano,
2014). C-SSF starts search from C-MLP(J=1) and
then gradually increases the number of hidden units J
one by one until J
max
. When searching C-MLP(J), the
method applies reducibility mapping to the optimum
of C-MLP(J−1) to get two kinds of singular regions
b
Θ
αβ
J
and
b
Θ
γ
J
. When starting search from the singu-
lar region, the method employs eigenvector descent
(Satoh and Nakano, 2012), which finds descending
directions, and from then on employs complex BFGS
(C-BFGS). The general flow of C-SSF1.0 is given be-
low. Let {w
(J)
0
,w
(J)
j
,w
(J)
j
, j = 1,··· , J} denote param-
eters of C-MLP(J).
Here we give notes on the implementation used
in our experiments. In Algorithm 1, p in steps 1.1
and 2.1.1 is free and was set to −1, 0, and 1. More-
over, q in step 2.2.1 is also free and was set to 0.5,
1.0, and 1.5, which correspond to internal division,
boundary, and external division respectively. In Algo-
rithm 2, the golden section search (Luenberger, 1984)
was employed as a line search to find the suitable step
length.
C-SSF has the following characteristics (Satoh
and Nakano, 2014; Satoh and Nakano, 2015).
(1) The excellent solution of C-MLP(J) will be ob-
tained one after another for J=1,···,J
max
. C-SSF guar-
antees that training error of C-MLP(J) is smaller than
that of C-MLP(J−1) since C-SSF descends in C-
MLP(J) search space from the singular regions cor-
responding to the optimum of C-MLP(J−1). This
monotonic feature will be quite useful for model se-
lection. However, such monotonic decrease of train-
ing error is not guaranteed for existing methods.
(2) C-SSF runs without using random number, mean-
ing it always finds the same set of solutions.
A Yet Faster Version of Complex-valued Multilayer Perceptron Learning using Singular Regions and Search Pruning
123

Algorithm 1: C-SSF Method (ver 1.0 or 1.1).
step 1. Search for MLP(1)
1.1 Set an initial point on
b
Θ
αβ
1
:
w
(1)
0
←
y, w
(1)
1
← 0, w
(1)
1
← [p,0,··· ,0]
T
1.2 Search
from singular region
1.3 Store the best as bw
(1)
0
, bw
(1)
1
, bw
(1)
1
; J ← 2.
step 2. Search for MLP(J)
while J ≤ J
max
do
2.1 Search from
b
Θ
αβ
J
:
2.1.1 Set
an initial point on
b
Θ
αβ
J
2.1.2 Search
from singular region
2.2 Search from
b
Θ
γ
J
:
for m = 2,··· , J do
2.2.1 Set an initial point on
b
Θ
γ
J
2.2.2 Search
from singular region
end for
2.3 Get the best among all solutions obtained
in steps 2.1 and 2.2, and store it as bw
(J)
0
, bw
(J)
j
,
bw
(J)
j
, j = 1,··· ,J. Then, J ← J + 1.
end while
Algorithm 2: Search from singular region.
step 1. Calculate the Hessian and get all the nega-
tive eigenvalues and their eigenvectors.
step 2.
for each negative eigenvalue with its eigenvector u
do
2.1 Perform a line search in the direction of u,
start search using C-BFGS afterward, and keep
the solution.
2.2 Perform a line search in the direction of −u,
start search using C-BFGS afterward, and keep
the solution.
end for
3.2 Search Pruning
C-SSF1.0 stably found excellent solutions, better than
C-BFGS. However, it took several times longer than
C-BFGS because the number of searches got larger
and larger as the number of hidden units J increased.
Thus, a faster version C-SSF1.1 (Satoh and Nakano,
2015) was proposed by introducing search pruning.
The general flow of C-SSF1.1 is the same as Al-
gorithm 1 since search pruning is embedded in search
using C-BFGS at steps 2.1 and 2.2 of Algorithm
2. Although search pruning is explained in detail in
(Satoh and Nakano, 2015), the main point is shown
below.
Algorithm 3: Set an initial point on
b
Θ
αβ
J
.
w
(J)
0
← bw
(J−1)
0
,
w
(J)
1
←0, w
(J)
1
←[p, 0,··· ,0]
T
,
w
(J)
j
← bw
(J−1)
j−1
, w
(J)
j
← bw
(J−1)
j−1
, j=2,··· , J
Algorithm 4: Set an initial point on
b
Θ
γ
J
.
w
(J)
0
← bw
(J−1)
0
,
w
(J)
1
← q × bw
(J−1)
m−1
, w
(J)
1
← bw
(J−1)
m−1
,
w
(J)
m
← (1 − q) × bw
(J−1)
m−1
, w
(J)
m
← bw
(J−1)
m−1
,
w
(J)
j
← bw
(J−1)
j−1
, w
(J)
j
← bw
(J−1)
j−1
,
j ∈ {2, · · · ,J} \ {m}
Let θ
(t)
and φ
(τ)
be a current search point and
a point stored during a previous search respectively.
Since d = (··· ,d
m
,···)
T
is a normalizing vector, v
(t)
and r
(τ)
are normalized points. The normalization is
introduced to prevent any weight having a large abso-
lute value from influencing the decision too much.
d
m
←
1
θ
(t−1)
m
(1 < |θ
(t−1)
m
|)
(|θ
(t−1)
m
| ≤ 1)
(7)
v
(t)
← diag(d) θ
(t)
(8)
v
(t−1)
← diag(d) θ
(t−1)
(9)
r
(τ)
← diag(d) φ
(τ)
, τ = 1,··· , T (10)
Here m = 1,··· ,2M, where M is the number of com-
plex weights. Let T be the number of points stored so
far, and diag(d) is a diagonal matrix whose diagonal
elements are d.
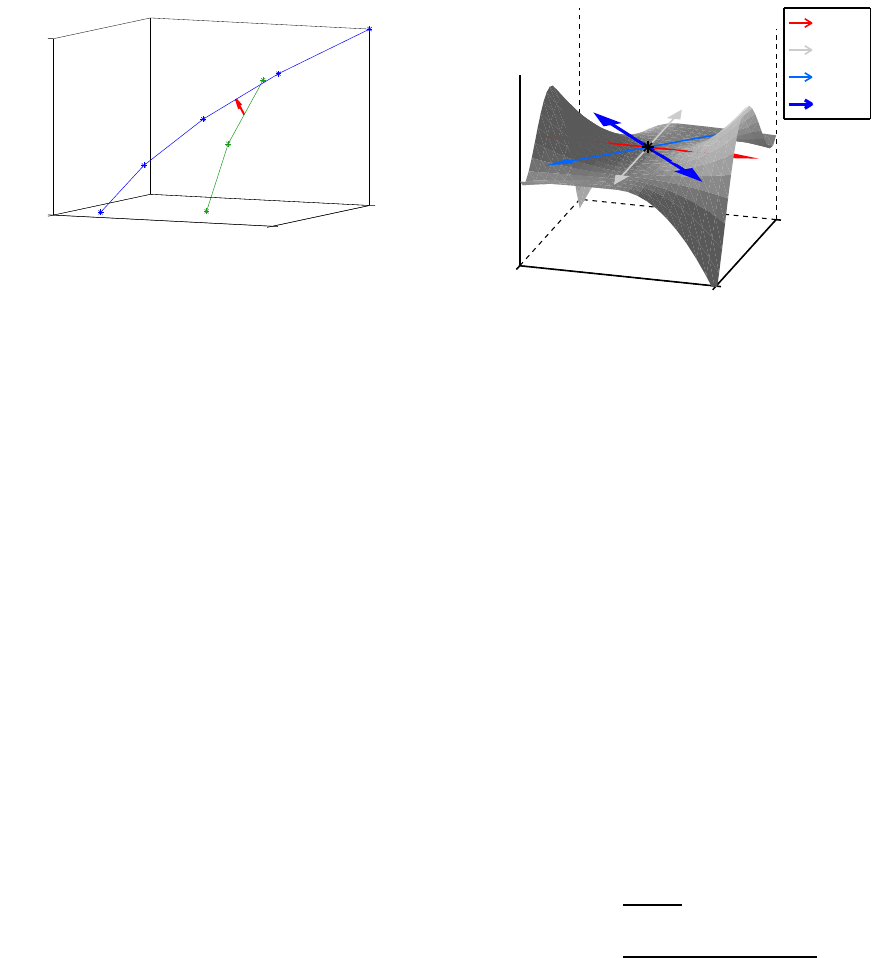
See Figure 1. Now consider a line L
1
through two
points r
(τ−1)
and r
(τ)
, and a line L
2
through two points
v
(t−1)
and v
(t)
. Then consider a line L
3
perpendicular
to each of L
1
and L
2
. Note that line L
3
includes the
shortest line segment ℓ between L
1
and L
2
. Based on
this ℓ, we decide whether the current search route is to
merge onto a previous search route. We can calculate
ℓ, which can be represented as below.
ℓ = (r
(τ−1)
+ a
1
∆r
(τ)
) − (v
(t−1)
+ a
2
∆v
(t)
) (11)
∆r
(τ)
≡ r
(τ)
− r
(τ−1)
, ∆v
(t)
≡ v
(t)
− v
(t−1)
By solving min
a
ℓ
T
ℓ, unknown a
1
and a
2
can be de-
termined. The following are the condition for ℓ to
start from a point between v
(t−1)
and v
(t)
and to end at
a point between r
(τ−1)
and r
(τ)
.
0 ≤ a
1
≤ 1, 0 ≤ a
2
≤ 1 (12)
If ℓ does not satisfy the condition eq.(12) for any τ =
1,··· ,T, we consider the current search route does
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
124
r
(τ)
v
(t)
r
(τ−1)
l
v
(t−1)
v
(t−2)
r
(τ−2)
r
(τ−3)
r
(τ−4)
Figure 1: Conceptual Diagram of Search Pruning of C-
SSF1.1.
not merge onto any previous route. If the condition
holds for a certain τ, however, we check whether the
current search is to be pruned. The current search is
pruned if the absolute value of each element of ℓ is
smaller than predefined ε.
Here implementation details in our experiments
are described. Checking of search pruning and stor-
ing of current points are carried out at intervals of 100
search steps. Moreover, we set ε = 0.3 for a threshold
of search route proximity.
3.3 Proposed Method: C-SSF1.3
C-SSF1.1 ran a few times faster than C-SSF1.0 with-
out losing the excellent solution quality, but still re-
mained unsatisfactory in processing time for a larger
model. C-SSF1.1 needed to be made even faster; thus,
this paper proposes a yet faster version C-SSF1.3.
Since the key point is to decrease the number of
searches, we decided to put a ceiling S
max
on the
number; however, we should not lose excellent so-
lutions by doing so. All of the limited number S
max
of searches should start in the promising directions.
Note that the decision whether or not this direction
will lead to an excellent solution should be made at a
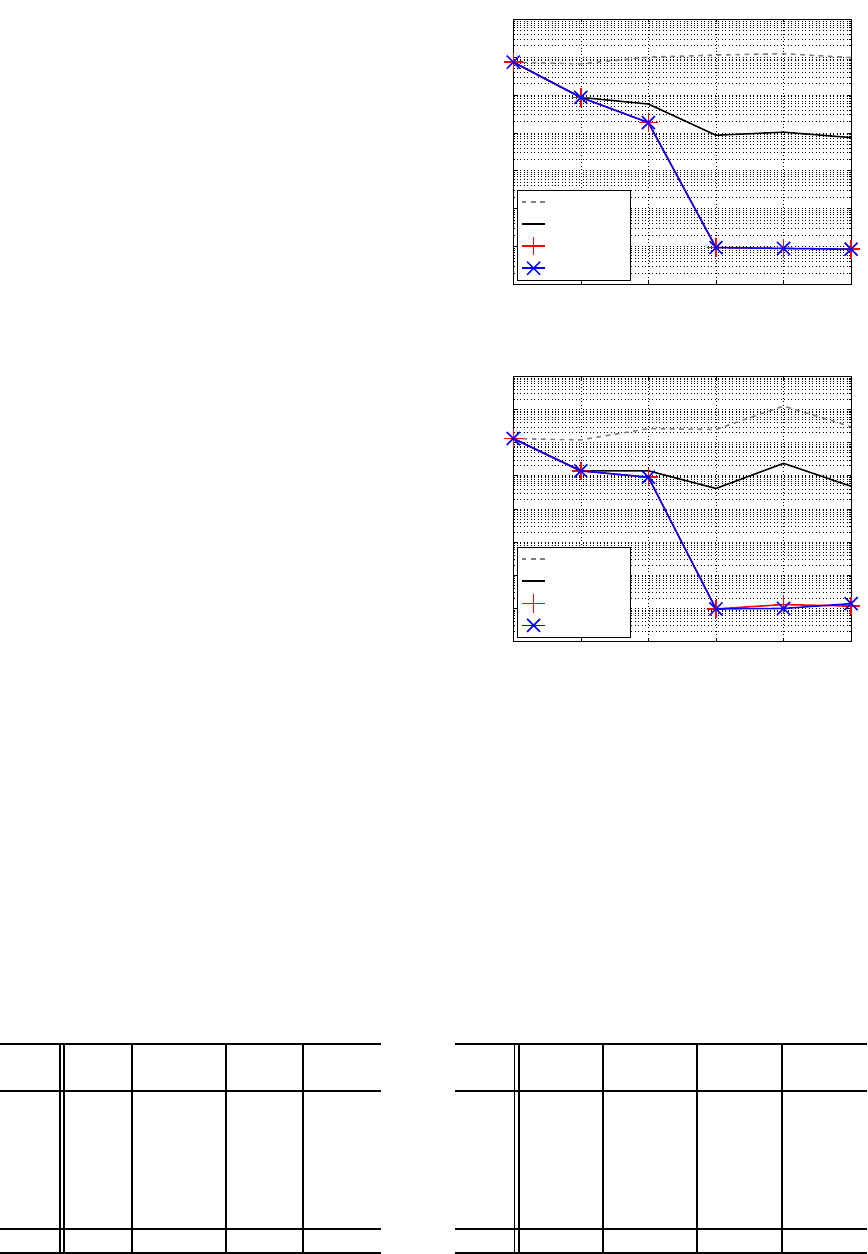
starting point. We assumed the larger convex curva-
ture at a starting point, the better solution at the end
of the search. See Figure 2.
To implement this, we calculate eigenvalues of
all initial points on the singular regions
b
Θ
αβ
J
and
b
Θ
γ
J
.
Then, we pick up the limited number of eigenvalues
in ascending order, and perform search using their
eigenvectors.
One more contrivance was introduced into C-
SSF1.3. When C-SSF starts search at one step larger
C-MLP(J), only the best solution of C-MLP(J−1) is
used to create the singular regions. Recently we found
that the best solution of C-MLP(J−1) does not always
lead to the best solution of C-MLP(J) especially for a
very small J. Therefore, we utilize the best R solu-
tions of C-MLP(J−1) to create the singular regions
E
λ
1
(>0)
λ
2
(=0)
λ
3
(>λ
4
)
λ
4
(<λ
3
)
Figure 2: Conceptual diagram of eigenvectors at a point in
a singular region.
of C-MLP(J) when J ≤ J
R
. Note that when J ≤ J
R
,
the ceiling on the number of searches is not put. The
increase of processing load due to additional searches
will be trivial because J is very small.
In the following experiments, C-SSF1.3 system
parameters were set as S
max
= 100, J
R
= 3, and R =
3.
4 EXPERIMENTS
The proposed C-SSF1.3 was evaluated using two arti-
ficial data sets. That is, the performance of C-SSF1.3
was compared with former version C-SSF1.1, batch-
type complex BP with line search (C-BP), and com-
plex BFGS (C-BFGS).
In a C-MLP an activation function plays an impor-
tant role. We employed the following σ(z) (Kim and
Guest, 1990; Leung and Haykin, 1991) for a hidden
unit. When z is a complex number (z = a+ i b), σ(z)
is periodic and unbounded.
σ(z) =
1
1+ e
−z
=
1+ e
−a
cosb+ ie
−a
sinb
1+ 2e
−a
cosb+ e
−2a
(13)
Real and imaginary parts of initial weights for C-
BP and C-BFGS were randomly selected from the
range (−1,1). For each J, C-BP or C-BFGS was per-
formed 100 times changing initial weights.
Each run of any learning method was terminated
when the number of sweeps exceeded 10,000 or the
step length got smaller than 10
−16
.
A Yet Faster Version of Complex-valued Multilayer Perceptron Learning using Singular Regions and Search Pruning
125
4.1 Experiments using Artificial Data 1
Artificial data 1 was generated using a C-MLP hav-
ing the following weights with J = 4. A PC with In-
tel(R) Xeon(R) E5-2687W 3.10GHz and 32GB mem-
ory was used together with MATLAB2014a.
(w
0
,w
1
,w
2
,w
3
,w
4
)
= (−3+ 1i,−1+ 1i,1+ 1i,0+ 5i,5− 4i),
(w
1
,w
2
,w
3
,w
4
)
=
−2+ 3i 0− 5i −4− 5i −1+ 1i
4+ 0i −2+ 2i −1+ 2i −2+ 2i
−3+ 1i 0− 2i −4− 4i 4+ 1i
4+ 4i 1+ 4i 3+ 0i −4− 1i
0− 5i 5+ 3i −1− 5i 3− 1i
−5− 2i −4+ 2i 3− 5i 5+ 4i
(14)
The real and imaginary parts of input x
k
were ran-
domly selected from the range (0,1). Teacher sig-
nal y
µ
was generated by adding small Gaussian noise
N (0,0.01
2
) to both real and imaginary parts of the
output. The size of training data was 500 (N = 500),
and the maximum number of hidden units was set to
6 (J
max
= 6). Test data of 1,000 data points without
noise was generated independently of training data.
Figures 3 (a) and (b) show minimum training er-
ror and the corresponding test error respectively. C-
BP could not decrease training error and showed very
poor generalization. C-BFGS basically decreased
training error as J got larger; however, its test error
showed the slight up-and-down movement. Both fast
versions of C-SSF showed much the same results for
training and test, much better than those of C-BFGS
for J ≥ 4. Note also that C-SSF monotonically de-
creased training error. Both versions of C-SSF and
C-BFGS minimized test error at J = 4, which is cor-
rect.
Table 1 shows the number of searches for artifi-
cial data 1. The numbers of each C-SSF include the
ones of pruned searches. Note that the numbers of
each C-SSF for J = 2 or 3 were larger than 100 be-
cause multiple best solutions were utilized to create
starting points. The total number of C-SSF1.3 was 29
% (0.71=791/1108) smaller than that of C-SSF1.1.
Table 1: Numbers of searches for artificial data 1.
J C-BP C-BFGS C-SSF C-SSF
1.1 1.3
1 100 100 38 38
2
100 100 132 132
3 100 100 321 321
4
100 100 160 100
5 100 100 220 100
6
100 100 237 100
total 600 600 1108 791
1 2 3 4 5 6
10
−2
10
−1
10
0
10
1
10
2
10
3
10
4
10
5
Training error
J
C−BP
C−BFGS
C−SSF1.1
C−SSF1.3
(a) Training error.
1 2 3 4 5 6
10
−2
10
−1
10
0
10
1
10
2
10
3
10
4
10
5
10
6
Test error
J
C−BP
C−BFGS
C−SSF1.1
C−SSF1.3
(b) Test error.
Figure 3: Training and test errors for artificial data 1.
Table 2 shows CPU time required by each method
for artificial data 1. C-BP spent the longest time 443
minutes in total, which may mean it easily got stuck in
poor local minima, and could not escape from them.
C-SSF1.3 was 1.23 (=742/602) times faster than C-
SSF1.1, and C-BFGS was in the middle of the two.
CPU time required by C-BFGS increased as J got
larger, while CPU time of C-SSF at J = 3 was a bit
large due to using multiple best solutions for creating
starting points.
Table 2: CPU time for artificial data 1 (hr:min:sec).
J C-BP C-BFGS C-SSF C-SSF
1.1 1.3
1 0:35:38 0:00:30 0:00:13 0:00:13
2
0:53:57 0:00:53 0:00:39 0:00:39
3 1:10:27 0:01:08 0:03:09 0:03:09
4
1:39:13 0:02:18 0:01:19 0:01:00
5 1:22:45 0:02:35 0:02:56 0:02:07
6
1:41:25 0:03:54 0:04:06 0:02:53
total 7:23:24 0:11:19 0:12:22 0:10:02
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
126

4.2 Experiments using Artificial Data 2
Artificial data 2 was generated using the follow-
ing logarithmic spirals. How flexibly C-MLP can
represent this heavily swirling function was evalu-
ated. XPS 8300 with Intel(R) Core i7-2600 3.40GHz
and 12GB memory was used together with MAT-
LAB2014a.
y = {0.001e
0.1φ
+ 2.5e
−0.1φ
+ 0.1e
0.05φ
}
{e
2iφ
+ e
5i(φ+π/3)
+ e
12iφ
+ e
15iφ
},
where φ = 2πx (15)
The real part of input x
µ
was randomly selected from
the range (0,10), and the imaginary part was set to
zero. Teacher signal y
µ
was generated by adding small
Gaussian noise N (0, 0.01
2
) to both real and imag-
inary parts of the output. The size of training data
was 1,000 (N = 1,000), and the maximum number of
hidden units was set to 16 (J
max
= 16). Test data of
1,000 data points without noise was generated from
the range (10,13) of input x, outside of the range of
training.
Figures 4 (a) and (b) show minimum training
error and the corresponding test error respectively.
Again C-BP could hardly decrease training error and
showed very poor generalization. C-BFGS basically
decreased training error as J increased, but fluctuated
for J ≥ 12. Both versions of C-SSF showed almost
equivalent results for training and test, monotonically
decreasing training error. Both C-SSF versions indi-
cate J = 12 or 13 may be the best model.
Table 3: Numbers of searches for artificial data 2.
J C-BP C-BFGS C-SSF C-SSF
1.1 1.3
1 100 100 16 16
2 100 100 81 81
3
100 100 162 162
4 100 100 70 70
5
100 100 80 80
6 100 100 177 100
7 100 100 190 100
8
100 100 269 100
9 100 100 568 100
10
100 100 306 100
11 100 100 593 100
12
100 100 583 100
13 100 100 1042 100
14
100 100 770 100
15 100 100 1664 100
16
100 100 838 100
total 1600 1600 7409 1509
2 4 6 8 10 12 14 16
10
−1
10
0
10
1
10
2
10
3
10
4
Training error
J
C−BP
C−BFGS
C−SSF1.1
C−SSF1.3
(a) Training error.
2 4 6 8 10 12 14 16
10
1
10
2
10
3
10
4
10
5
10
6
Test error
J
C−BP
C−BFGS
C−SSF1.1
C−SSF1.3
(b) Test error.
Figure 4: Training and test errors for artificial data 2.
Table 4: CPU time for artificial data 2 (hr:min:sec).
J C-BP C-BFGS C-SSF C-SSF
1.1 1.3
1 0:38:58 0:01:03 0:00:10 0:00:10
2 1:11:01 0:01:46 0:02:16 0:02:18
3
1:12:26 0:03:38 0:05:27 0:05:33
4 1:29:03 0:04:47 0:03:00 0:03:07
5
1:39:42 0:06:10 0:03:17 0:03:25
6 1:55:47 0:07:22 0:08:27 0:07:08
7
2:11:15 0:09:22 0:09:16 0:06:26
8 2:22:59 0:11:08 0:14:34 0:07:46
9
2:33:36 0:13:54 0:22:46 0:06:55
10 2:54:17 0:15:51 0:13:31 0:06:27
11
3:04:18 0:18:23 0:30:37 0:07:39
12 3:20:16 0:19:35 0:24:39 0:07:27
13
3:49:26 0:22:03 0:38:24 0:09:32
14 4:00:40 0:26:08 0:24:32 0:06:28
15
4:12:06 0:25:33 1:04:22 0:06:42
16 4:33:26 0:28:11 0:31:31 0:07:02
total 41:09:15 3:34:55 4:56:48 1:34:04
A Yet Faster Version of Complex-valued Multilayer Perceptron Learning using Singular Regions and Search Pruning
127

−20
0
20
−20
0
20
0
5
10
Re(y )
Im(y )
x
f
Training data
Test data
(a) C-BP(J = 15)
−20
0
20
−20
0
20
0
5
10
Re(y )
Im(y )
x
f
Training data
Test data
(b) C-BFGS(J = 15)
−20
0
20
−20
0
20
0
5
10
Re(y )
Im(y )
x
f
Training data
Test data
(c) C-SSF1.1(J = 13)
−20
0
20
−20
0
20
0
5
10
Re(y )
Im(y )
x
f
Training data
Test data
(d) C-SSF1.3(J = 12)
Figure 5: Outputs of C-MLPs.
Table 3 shows the number of searches of each
method for artificial data 2. The numbers of each
C-SSF include the ones of pruned searches. The
numbers of each C-SSF for J = 3 were larger than
100 because multiple best solutions were utilized for
J ≤ 3. The total number of C-SSF1.3 was one-fifth
(0.20=1509/7409) of that of C-SSF1.1.
Table 4 shows CPU time required by each method
for artificial data 2. C-BP spent the longest CPU time
about 41 hours in total. CPU time of C-BFGS grad-
ually increased as J got larger, spending 3.6 hours in
total. C-SSF1.3 was the fastest, 3.2 times (=297/94)
faster than C-SSF1.1, and 2.3 times (=215/94) faster
than C-BFGS. Note that C-SSF1.3 spent about 6 or
7 minutes for each J (≥ 6) except J=13, while C-
SSF1.1 showed a tendency to require more CPU time
as J got larger.
Figures 5 (a), (b), (c) and (d) show the output of
the best models learned by each learning method. The
best model means C-MLP(J) minimizing test error;
J=15 for C-BP and C-BFGS, J=13 for C-SSF1.1, and
J=12 for C-SSF1.3. C-BP could hardly fit the func-
tion for the range (0, 10) and showed very poor gener-
alization for the range (10,13). C-BFGS nicely fitted
the function in the range (0,10), but the amplitude fit-
ting got slightly deviated for the range (10,13). Both
versions of C-SSF very nicely fitted the swirling func-
tion all over the range (0,13) showing excellent gen-
eralization.
5 CONCLUSION
C-SSF is a completely new learning method for a
complex-valued MLP, making good use of singular
regions to stably and successively find excellent so-
lutions. We proposed C-SSF1.3 which puts a ceiling
on the search load for larger models and utilizes mul-
tiple best solutions for smaller models. Although the
former versions of C-SSF were rather slow, the pro-
posed C-SSF1.3 ran very fast without losing excellent
solution quality. It ran 3.2 times faster than C-SSF1.1,
2.3 times faster than C-BFGS for a larger problem. In
the future we plan to apply the method to challenging
applications.
ACKNOWLEDGEMENTS
This work was supported by Grants-in-Aid for Sci-
entific Research (C) 25330294 and Chubu University
Grant 26IS19A.
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
128
REFERENCES
S. Amari: Natural gradient works efficiently in learning,
Neural Comput., 10(2), 251/276 (1998)
M.F. Amin and et al.: Wirtinger calculus based gradient de-
scent and Levenberg-Marquardt learning algorithms
in complex-valued neural networks, Proc. ICONIP,
550/559 (2011)
K. Fukumizu and S. Amari: Local minima and plateaus in
hierarchical structure of multilayer perceptrons, Neu-
ral Networks, 13(3), 317/327 (2000)
A. Hirose: Complex-Valued Neural Networks, 2nd ed.,
Springer-Verlag, Berlin Heidelberg (2012)
M.S. Kim and C.C. Guest: Modification of backpropaga-
tion networks for complex-valued signal processing in
frequency domain, Proc. IJCNN, 3, 27/31 (1990)
H. Leung and S. Haykin: The complex backpropaga-
tion algorithm, IEEE Trans. Signal Process., 39(9),
2101/2104 (1991)
D.G. Luenberger: Linear and nonlinear programming,
Addison-Wesley Publishing Company, Reading, Mas-
sachusetts (1984)
T. Nitta: Reducibility of the complex-valued neural net-
work, Neural Information Processing - Letters and
Reviews, 2(3), 53/56 (2004)
T. Nitta: Local minima in hierarchical structures of
complex-valued neural networks, Neural Networks,
43, 1/7 (2013)
S. Satoh and R. Nakano: Eigen vector descent and line
search for multilayer perceptron, Proc. IAENG Int.
Conf. on AI & Applications (ICAIA’12), 1 1/6 (2012)
S. Satoh and R. Nakano: Fast and stable learning utiliz-
ing singular regions of multilayer perceptron, Neural
Processing Letters, 38(2), 99/115 (2013)
S. Satoh, and R. Nakano: Complex-valued multilayer per-
ceptron search utilizing singular regions of complex-
valued parameter space, Proc. ICANN, 315/322
(2014)
S. Satoh, and R. Nakano: Complex-valued multilayer per-
ceptron learning using singular regions and search
pruning, Proc. IJCNN (to be published) (2015)
H.J. Sussmann: Uniqueness of the weights for minimal
feedforward nets with a given input-output map, Neu-
ral Networks, 5(4), 589/593 (1992)
S. Suzumura and R. Nakano: Complex-valued BFGS
method for complex-valued neural networks, IEICE
Trans. on Information & Systems, J96-D(3), 423/431
(in Japanese) (2013)
A Yet Faster Version of Complex-valued Multilayer Perceptron Learning using Singular Regions and Search Pruning
129
