Evolving Four Part Harmony using a Multiple Worlds Model
Marco Scirea
1
and Joseph Alexander Brown
2
1
Center for Computer Games Research, IT University of Copenhagen, Copenhagen, Denmark
2
Artificial Intelligence in Games Development Lab, Innopolis University, Innopolis, Republic of Tatarstan, Russia
Keywords:
Genetic Algorithms, Procedural Content Generation, Music.
Abstract:
This application of the Multiple Worlds Model examines a collaborative fitness model for generating four part
harmonies. In this model we have multiple populations and the fitness of the individuals is based on the ability
of a member from each population to work with the members of other populations. We present the result of two
experiments: the generation of compositions, given a static voice line, both in a constrained and unconstrained
harmonic framework. The remaining three voices are evolved using this collaborative fitness function, which
looks for a number of classical composition rules for such music. The evolved music is found to meet with
the requirements placed on it by musical theory. Using the data obtained while running our experiments we
observe and discuss interesting qualities of the solution space.
1 INTRODUCTION
A great variation of techniques have been used for
the generation of music material. A large number
of algorithms have been researched and explored in
this particular application. This might be because
music is, to a certain degree, quantifiable and ab-
stract. There exists artificial intelligence systems that
can produce very high quality music. (Cope, 1991)
is focused on codifying music styles is very inter-
esting and many more approaches are described by
(Miranda, 2013). These algorithms can range from
creating entire pieces of music, to solving specific
problems (for example how to do a transition from a
phrase A to a phrase B), to being a compositional aid
and many more applications. Evolutionary algorithms
have been a popular technique to use in this kind of
application as this approach, based on the concept of
random variation and selection, can efficiently search
a large solution space. Notable works using this ap-
proach are (Dahlstedt, 2007) on evolving complete
piano pieces, (Hoover et al., 2011) using interactive
evolution of accompaniments, and (Miranda, 2003)
in the evolution of music in artificial life societies.
The Multiple Worlds Model (MWM) (Brown and
Ashlock, 2010) is an evolutionary approach which
uses a multiple population approach with a collabora-
tive fitness function between the populations. It uses
multiple evolving populations acting upon the same
target optimization, not unlike island models (Whitley
et al., 1997). However, island models have the goal of
providing a single solution to a problem and pass ge-
netic traits to each other by an explicit migration step.
The chromosomes in an island model are part of the
same species as they breed amongst themselves. The
multiple worlds model separates these populations on
the genetic level, they are separate species under the
biological species definition — they do not interbreed,
due to biological infertility, or behavioral differences.
The goal of the MWM is not to provide a single good
solution, but a set of interacting solutions.
Previous examples of MWM have been demon-
strated to split and join sets of iterated prisoners
dilemma playing agents and produce new agents
(Brown, 2012; Brown, 2013; Brown, 2014). (Ashlock
and McEachern, 2011) used a MWM in order to sim-
ulate the biological networks produced by species of
bacterium using game theory. Further, it has been
used to model the splits in a radio station market
based on the preferences of listeners in the demo-
graphic area (Brown, 2014). Each of the populations
represents a radio playlist and fitness is defined by
a set of listeners who change stations based on an
enjoyment value. These studies of the MWM have
been competitive, each of the species is fighting over
food resources. This study has a collaborative aspect,
with each of the species, a single musical voice, hav-
ing to construct a which avoids conflict with other
voices. Similar process of divergence are seen in
roots, leaves, and seed structures of plants with a his-
220
Scirea, M. and Brown, J..
Evolving Four Part Harmony using a Multiple Worlds Model.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 220-227
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tory of coexistence (Tilman and Snell-Rood, 2014).
This process is known as Adaptive radiation. The
properties of this species were first fully examined
by (Lack, 1947) and were not used by Darwin’s ex-
aminations due to a number of misclassifications in
the species caused by poor record keeping (Sulloway,
1982). Finches were found to have large changes to
their phenotypic traits in even short periods of time
due to changes in food sources (Grant and Grant,
1979; Grant and Grant, 1982; Grant and Grant, 1983).
Furthermore, behavioural modification can also
lead to specialization in food sources through a pro-
cess of niche partitioning. Hanson in Feathers gives
an anecdotal account of studying the behaviours of
North American bird actions in a forest: “Nuthatches
foraged mostly on the trunks, Chickadees dominated
the main branches, and Kinglets spend their time flit-
ting about in the side branches” (Hanson, 2011). The
MWM aims to use such principles of inter-population
competition with intra-population evolution to guide
a process of partitioning into models.
The niche effect is intrinsic to MWM. It does
not require an explicit calculation of phenotype dis-
tance, or a crowding measure, the novel method of
fitness evaluation is implicitly making crowding un-
desirable. It has also been shown to increase the
diversity of final solutions of the creation of multi-
ple models (Brown, 2014). This diversity has been
seen in studies of mixture vs. monoculture plants in
(Zuppinger-Dingley et al., 2014), which examined the
results of eight years of experimental growth in Jena,
Germany. It showed there was an increased interspe-
cific difference to those plants grown in mixture types
compared (P < 0.05) and intraspecific distance within
mixture types on traits was increased (P = 0.101).
They attribute a difference in relative specific leaf area
(P = 0.073) and height (P = 0.074) to specialization
into a niche. While these findings where marginally
significant correlations, the authors claim that these
traits are representative of relevant niche dimensions,
and that further study is warranted looking at the pro-
cesses of change. (Tilman and Snell-Rood, 2014) ex-
amine this study, and the previous mentioned finch
studies, to question if such studies can experimentally
demonstrate a divergence of species.
This study examines the application of the adap-
tive radiation by the MWM on the creation of a four
part harmony in which one of the voices is known.
The remainder of this paper is organized as follows:
Section 2 examines the problem of creating a four part
harmony as an evolutionary process, with Section 3
explaining the compositional rules used by the gener-
ator. The Multiple World Model of evolutionary algo-
rithm is examined in Section 4, with special attention
Figure 1: Ranges for the four voices used in four-part har-
mony.
to the collaborative model of fitness. Section 5 de-
scribes the experimental setting of the system used to
demonstrate the method. The results of these experi-
ments are examined in Section 6. Section 7 gives con-
clusions sets out further directions for this process.
2 FOUR PART HARMONY
Four-part harmony defines the category of music writ-
ten for four voices (which could be singers or musi-
cal instruments) where the four parts produce a note
for each chord in the piece. The four voices are gen-
erally called soprano (or treble), alto (contralto or
countertenor), tenor, and bass (Boldrey, 1994). These
voices all have some classically defined ranges (see
figure 1), the origin of which comes from the limits
of human singers: most singers have a vocal range
of two octaves (McKinney, 1982), which means that
most bass singers won’t be able to reach the higher
notes of a tenor or of a soprano. Typically the higher
voice will perform a melody while the lower three
will harmonize it, in our study any melody arising in
the higher voice is going to be purely a by-product
of evolution, as we do not interfere with its creation.
Nonetheless, it’s worth noting that this doesn’t mean
that interesting melodies cannot emerge.
This type of music (also called chorale) has slowly
evolved from Gregorian chant, which was unison
choir), becoming predominant in the Renaissance era,
where its role as sacred music in Western Europe
made it the main type of formally notated music. It
has been explored by innumerable artists and later
(Baroque and Classical music) accompanied by var-
ious types of instrumentation. Examples are Bach’s
Mass in B minor, Mozart’s Mass in C minor, Haydn’s
The Creation and The Seasons. While all these works
are thought to be for use in sacred ceremonies, the
use of choirs (and chorale) soon after expanded to
the concert stage, first examples of this tendency are
Berlioz’s Te Deum and Requiem, and Brahms’s Ein
deutsches Requiem.
We chose to explore the usage of evolutionary al-
gorithms in creating this style of compositions as the
composition style is commonly used as a teaching ex-
Evolving Four Part Harmony using a Multiple Worlds Model
221

ercise for composers to learn to manage and create
harmonies (Sessions, 1951). This exercise is partic-
ularly effective as the student must control both the
horizontal and vertical dimensions of the texture. This
strictly limited style of composition also provide us
with a good benchmark to test the Multiple Worlds
Model in the field of music generation.
We though it was interesting to consider each
voice as a single individual, by using this assumption
the MWM approach seemed a very interesting way to
evolve cooperatively such compositions. These indi-
viduals are part of different populations that evolve at
the same time, but without exchange of genetic mate-
rial between them. We expected the populations (ini-
tialized randomly) to then achieve speciation, evolv-
ing in a way that the individuals from one population
would evolve to “work well” with the voices belong-
ing to the other populations.
3 SELECTED RULES FOR FOUR
PART HARMONY
In this section we describe the rules of four-part har-
mony composition we decided to apply in this study,
these are going to form the fitness function for the
evaluation of the evolved individuals (see Section
4.3). We should note how the rules that we chose are
just a subset of four-part harmony rules; many of the
rules presented in various composition manuals are to
be considered “guidelines” for “good” composition,
so they can, in particular cases (stylistic, harmonic,
or melodic reasons), be ignored (Schoenberg, 1978).
The rules we chose consist of the strongest rules, the
ones that should always, apart from extreme cases, be
followed (Sessions, 1951).
Rule 1: for each beat each of the four voices plays
one of the notes of a triad, with only one of the
voices doubling a note one of the other voices are
playing. This rule prevents usage of alterations,
practically limiting the expression of chords to the
diatonic triad appropriate for the degree consid-
ered (eliminating for example possible diminished
chords). This rule would be considered “strong”
mostly in a pedagogical context, but for this first
study we believed it would be enough to consider
the smaller problem space defined by this rule.
Rule 2: avoid voice mixing. By voice mixing we
mean the situation where a higher voice plays a
note lower in pitch than what a lower voice is
playing. For example in the case where the so-
prano plays a C
4
while, at the same time, the
alto plays a D
4
. This situation is possible, as the
ranges of the voices overlap, but in this type of
composition it is not recommended.
Rule 3: no parallel octaves. Parallel octaves happen
when two voices, which have between each
other an interval of an octave, move by parallel
motion to two new notes that still create an
interval of an octave. This type of motion must
be avoided, as it destroys the independence of
the voices, by creating the sense of not two
voices, but of one voice doubled at the octave.
G
4
4
Forbidden
ˇ
ˇ
ˇ
ˇ
2
Forbidden
ˇ
ˇ
ˇ
ˇ
Rule 4: no parallel perfect fifths. Parallel fifths
work exactly like the previously described
parallel octaves, obviously with intervals of a
fifth. In the same way they convey the sense
of a single voice doubled and should then be
always avoided. A parallel fifth movement
can be accepted if it goes from a perfect 5th
to a diminished 5th if the notes of the dimin-
ished 5th resolve. However, as we already
explained, rule 1 prevents the creation of dimin-
ished intervals, so we can ignore this exception.
G
4
4
Forbidden
ˇ
ˇ
ˇ
ˇ
2
Forbidden
ˇ
ˇ
ˇ
ˇ
4 MULTIPLE WORLDS MODEL
4.1 Collaborative Fitness Model
In this study there is a change to the fitness evaluation
from previous models, while previous models were
looking at a competitive this application is collabora-
tive. It implements the collaborative model of fitness
proposed in (Brown, 2014), that each member of a
world is scored the same as the world score, rather
than the individual being given points only if it cap-
tures the modeled point better than the other models.
This makes the fitness not just dependant upon a sin-
gle voice, but on how it interacts with other voices in
the model.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
222

for some number of generations do
randomize the worlds
for all worlds do
for all datapoints do
(competitive) award the point to the model with the best fitness
(collaborative) award the same fitness to each model based on their com-
bined ability to solve the problem
end for
end for
for all populations do
Select breeding pairs based on fitness
Apply Crossover/Mutation
end for
end for
Figure 2: Demonstration (collaborative models) and Pseu-
docode (competitive and collaborative models) of the Mul-
tiple Worlds system.
4.2 Genome Representation
The genome representing an individual (or voice line)
is composed of an array of n integers, where n is the
amount of notes of the given bass line or a user de-
fined number if the bass line is left free to evolve
with the other voices. These integers represent the
amount of semi-tones from the lower note of the
voice’s range, for example this means that the so-
prano’s genes can go from 0 (C
4
) to 19 (A
5
).
We can express each note belonging to the range,
allowing us to evolve melodies fitting any key, even
if the rules we selected (see Section 3) prevent alter-
ations inside a specific key.
4.3 Fitness Evaluation
The rules discussed in Section 3 are implemented as
fitness penalties. The evolution aims to minimize the
number of violations of this rule set, each with an as-
sociated penalty score. A fitness score of zero is an
arrangement with no rules violations. Therefore, it is
a ‘valid’ composition.
f itness =
n
∑
i=0
(Double(s
i
,a
i
,t
i
,b
i
)+
+ 10 ∗ Mixing(s
i
,a
i
,t
i
,b
i
) + 30 ∗ Stuck(s
i
,a
i
,t
i
,b
i
))+
+
n−1
∑
i=0
(10 ∗ Fi f th(s
i
,a
i
,t
i
,b
i
) + Octave(s
i
,a
i
,t
i
,b
i
))
(1)
As you can see from equation 1 we have all the four
rules we discussed before: we check for each set of
notes to form a triad with one voice doubling one
of the others (Double), we check for voice mixing
(Mixing), for parallel fifths (Fi f th) and parallel oc-
taves (Octave). We also had to add an extra part in
the fitness function: Stuck. This function checks if a
voice is in the situation where, between the voice
above and the one below, there is less than 7 semi-
tones. If this is so, we can have the situation where
the two other voices are occupying pitches which are
“good” (they satisfy the doubling rule) and the middle
voice is stuck in a loop trying to reach one of the two
pitches that are already occupied effectively bringing
evolution to a dead end(note that most of the problem
comes from the voices having limited, different and
partly overlapping ranges). With the introduction of
this part of the fitness function we can avoid these sit-
uations, and as it is a very unwanted situation it has a
weight modifier of 30.
The Double function creates a proximity matrix
of the notes that are being evaluated in respect to the
possible pitches that can compose the triad, then it
calculates and returns the minimum distance (in semi-
tones) from an acceptable solution. For each couple
of adjacent voices Mixing checks if they have over-
lapped, so for example if the alto is playing a note
above the soprano or below the tenor. Octave and
Fi f th check for each possible couple of voices if they
for a parallel octave or fifth between the notes at the i
index and the i + 1. Mixing, Stuck, Octave and Fi f th
are boolean functions, yet they represent violations of
very strong rules, which is why they have a fairly high
weight modifier.
Evolving Four Part Harmony using a Multiple Worlds Model
223
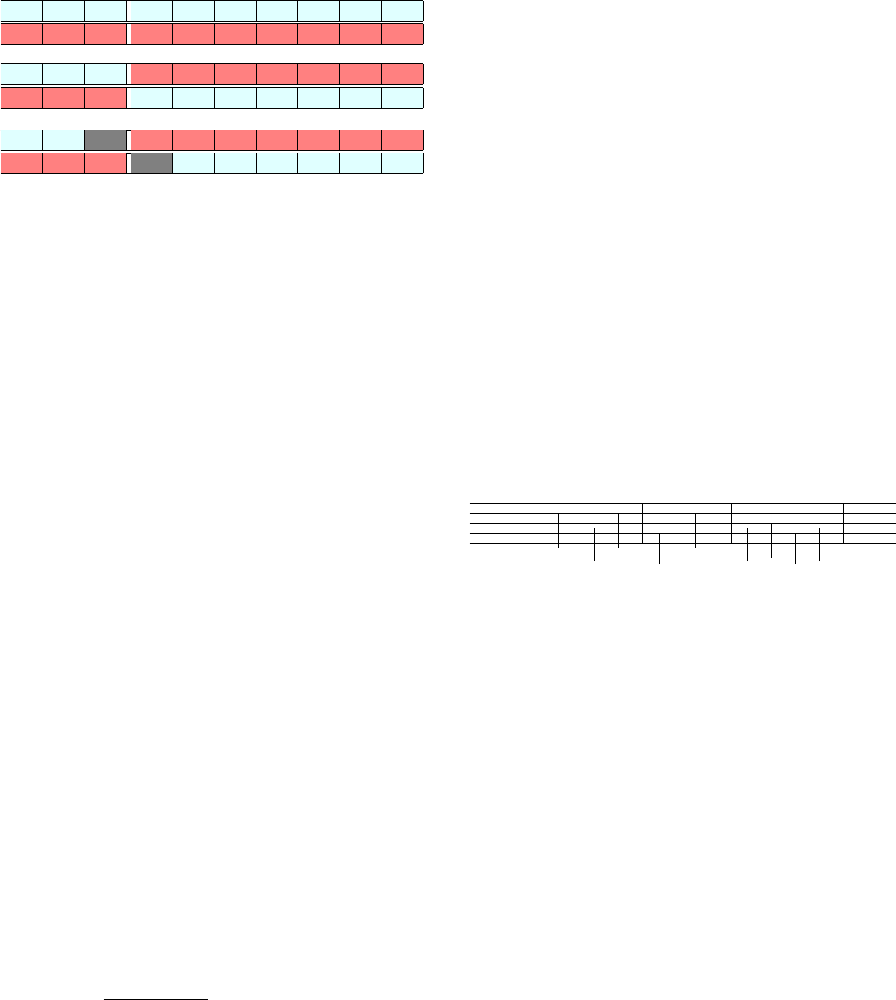
Parents
Children
Mutations of the Children
Figure 3: Example of breeding (crossover and mutation)
between the representations of notes. Parent one is the first
note sequence of size ten in light blue. Parent two is the
second note sequence of size ten in the darker red. A one-
point crossover then occurs between the two parents at the
third loci creating child one and two. The mutations of the
children then happen in child one at the third position and
the second child at position four, labeled in dark gray.
4.4 Selection
First, an elitist strategy is applied, copying to the new
generation the best individual of the current genera-
tion, the rest of the population is filled with offspring
from individuals selected by a simple tournament se-
lection algorithm (Miller and Goldberg, 1995). Fi-
nally, a mutation chance for each individual of the
new generation (1%) is applied. This is a low mu-
tation rate of the best individuals that this should help
to avoid inbreeding and promote exploration of the
problem space.
4.5 Variation Operators of Crossover
and Mutation
In this section we discuss how we have implemented
the production of a new generation; remember that we
have three (or four, depending on the setup) popula-
tions, the following method is applied to all of these.
We apply a simple one-point crossover: given two
parents we select randomly a point in their genomes
and create two new individuals containing the data
from one parent up to the crossover index and the data
from the other parent afterwards (see Figure 3).
When we mutate an individual, we give each gene
a chance of
1
NumberO f Genes
to mutate, effectively ob-
taining in general only one gene mutation per indi-
vidual mutation, but allowing for more (or no) muta-
tion. As we discussed in Section 4.2, each gene rep-
resent a note; when a gene mutates we take a random
point from a Gaussian distribution bound in the inter-
val [−5,5] and transform the note by adding the value
obtained in semi-tones. For example, if our gene rep-
resents a C
4
and we obtain a -2 from our random se-
lection, we subtract two semitones from C
4
obtaining
an A]
3
/B[
3
.
5 EXPERIMENTAL SETTINGS
We have conducted two trial run consisting of 100
evolutions of a four-part harmony composition given
an already written bass line. This choice was mo-
tivated firstly to try to simulate typical pedagogical
exercises in composition (where generally one of the
voices is already given to the students, which then
have to write the remaining three) and secondly be-
cause it seemed a more complicated problem for our
evolutionary approach. The difference between the
two trial was the introduction of a constraint: forcing
the note played by the bass to be always the root of
the chord. The introduction of the constraint allows
us to explore if we can generate variations within the
same harmonic framework. Indeed, we have observed
(but will not discuss in this paper) that the evolution-
ary process has much more success if given freedom
to also evolve the bass line. This stands to reason, as
giving a static bass line restricts the solution space,
effectively giving less freedom to the evolution.
I
2
4
4
˘
ˇ
ˇ
2
˘
˘
3
ˇ
ˇ
ˇ
ˇ
4
¯
We have obtained 85 solutions from the evolution
of compositions without the constraint, while out of
the 100 runs with the constraint we have only ob-
tained 8 solutions, those with a fitness score of 0, de-
noting no rules violations. You can access the midi
of solutions/non-solutions for the two experiments at
msci.itu.dk/fourpart. Often the evolution gets stuck in
local optima from which it cannot move out with our
current approach.
6 RESULTS AND DISCUSSION
The mean fitness of the populations proceeds to reach
a plateau after 120 generations, this seems to indi-
cate that evolution progresses correctly to a optimum.
Sadly most of the times in the constrained experiment,
instead of finding a solution we get stuck in a local op-
timum. We should note that the evolution is also not
very expensive in time usage criteria: it takes about
one to two seconds to reach the plateau. This seems
to indicate how the solution space for our constrained
problem is composed by many suboptimal points.
We have calculated distance matrixes between
the solutions/non-solutions and between non-
solutions/non-solutions. These give us information
on how the solution space is composed. The distance
metric we used is fairly naive, when confronting two
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
224

different evolved compositions we check how distant
(in amount of semitones) each note of each voice is
compared to it’s counterpart in the other composition.
We are aware that there are better distance measures
(like the Tonal Pitch Step Distance (De Haas et al.,
2008)), but most focus on harmonic distance. In our
constrained case this would make little sense between
solutions, as we defined a harmonic constraint on the
given bass’s notes always being the root of the chord.
In this paper we will focus on the data gathered
through the constrained experiment, as it gives us
some more interesting information on the solution
space of variations with the same harmonic structure.
6.1 Constrained Experiment Results
We have conducted an unpaired t test on the distances
between the solutions and between the non-solutions.
The mean minimum distance between the eight so-
lutions ( ¯x = 34.5, σ = 26.2) and the minimum dis-
tance from one of erred pieces the to one of the solu-
tions ( ¯x = 55.3, σ = 17.7) was found to be statistically
significantly lower (p = 0.0304) using a two-tailed t-
test between means. Thus, there is in general more
similarity between the closest correct pieces to each
other than the errors being close to the known solu-
tions. This implies that either the known solutions are
valleys in the search landscape which more than one
non-conflicted song exists in with a number of local
optima to bypass or that there are other unknown good
songs which are also moving the population. A pos-
sible explanation for this phenomenon might be given
by the harmonic constraints we have introduced. We
expect that by lifting such a constraint we will have
well distributed solutions, that might still cluster de-
pending on the harmonic qualities of the composi-
tions.
In the eight solutions, there are two pairs of ar-
rangements with close features, less than twenty units
of the distance measure. Yet, the same arrangement
was never found twice, demonstrating the diversity
of solution which is present due to the genetic ap-
proach. This makes for eight unique songs meeting
with the baseline, see Fig. 4 for all the solutions, we
highlight two very similar ones and two very different
ones. For comparison we also present a human-made
solution from the Genevan Psalter (Fig. 5). Note that
the notes that appear in the solution with a diesis (])
correspond in this key not to a A] but to a B[, which
appears normally in Fig. 5, because the B[ is included
in the key notation. They all share some common
chords and characteristics. This is due, as already dis-
cussed, to the harmonic limitations we have enforced
on the compositions. Yet, we obtain some different
Figure 4: The eight solution obtained by the constrained
experiment. The distances between solution 7 and solution
6 is 76 (semitones), while the distance between the solution
7 and solution 8 is only 6.
notes dispositions, that show how we can obtain many
variations even considering this limitations. We can
especially see this between the second and third solu-
Evolving Four Part Harmony using a Multiple Worlds Model
225
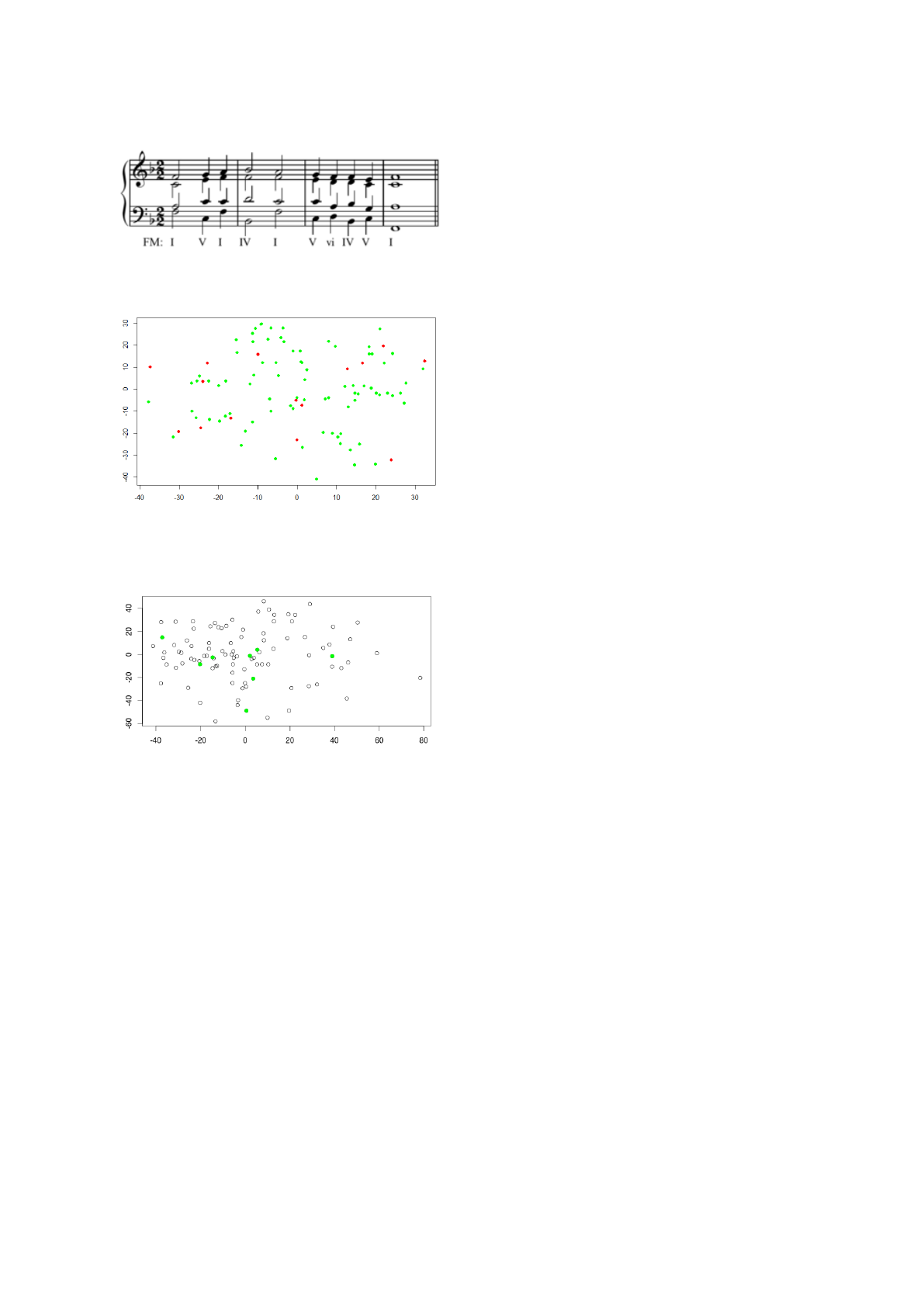
Figure 5: An example of human composed four part har-
mony using the same bass line and harmonic sequence,
from the Genevan Psalter: Old 124th.
Figure 6: Representation of the distance matrix calculated
for all runs in the unconstrained experiment calculated us-
ing Multidimensional Scaling. In green you can see the so-
lutions we found.
Figure 7: Representation of the distance matrix calculated
for all runs in the constrained experiment calculated using
Multidimensional Scaling. In green you can see the solu-
tions we found.
tion which, while being very similar still have man-
aged to present some small variation. The variation
in question appears at the 7th crotchet (which, in this
case, corresponds with the 7th beat), where we have
(from the bass to the soprano) {D, F, A, D} for the
second score and {D, D, A, F} for the third one. Even
if the voices are still doubling the root of the chord,
the three free voices sing different notes.
6.2 Unconstrained Experiment Results
Out of 100 runs we obtained 85 solutions when we
allow the algorithm to choose which voice plays the
root of the chord. This means that, as we still are giv-
ing a static bass line, the algorithm can choose one
of three possible chords to build per each bass note.
This is because the bass note can then be interpreted
as the root of the chord, as its third or its fifth; so if
the bass note is F, the possible chords would be F,
Dminor and B[. It should be noted that these com-
positions might present weird chord sequences, as the
choice of which of the three possible chords to choose
is stochastic and the algorithm has no information or
rules about chords. We have not conducted an study
to investigate these aesthetic questions yet, but we be-
lieve most compositions sound pleasant (you can find
the solutions at msci.itu.dk/fourpart).
We found no statistically significant relationship
between distances of solutions and non-solutions as
in the Constrained experiment. This seems to suggest
that these solutions occupy more evenly the solution
space and the same seems true for the non-solutions
(see Figure 6). We believe these result make sense:
we are exploring a wider search space and our algo-
rithm then is able to find more solutions without get-
ting stuck in local optima. This also helps us interpret
the results from the Constrained experiment: that ex-
periment had some constraints that limited the accept-
able solutions to a specific part of the solution space,
which would explain why they seems to be grouped
in a valley. That might be an indicator that our fit-
ness function has issues navigating through the solu-
tion space when the individual is far away from any
possible solutions.
7 CONCLUSION
In this paper we present a novel approach to gen-
erating four-parts harmonies by using the Multi-
ple Worlds Model evolutionary approach. We have
shown how we can generate multiple compositions
correctly, which present variations within and outside
a harmonic constraint. This study also allowed us
to notice the solution space, for constrained music,
appears to be composed by many suboptimal points.
Their is a solution valley where some of the most sim-
ilar found cluster.
At this time we cannot say that we can generate
better harmonies than other approaches, in fact our
ruleset is restricted.While rule based expert systems,
e.g. CHORAL (Ebcio
˘
glu, 1988), or the use of plan-
ning (Yi and Goldsmith, 2007) might create just as
good compositions or even better compositions. The
variety of solutions offered by our approach is very
interesting. A user using this system to harmonize a
voice line would, instead of having to be happy with
the one solution the system returns, be presented with
a variety of variations could be selected.
One of the major questions raised by this work
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
226
is the issue of human competitive performance of
the result. This can be first demonstrated by show-
ing that the system given a baseline will produce the
same composition as a human composer. The best
method of testing the claim to human competitive per-
formance would be for this system along with a group
of student musicians to be given the same set of base-
lines in a larger study. The generated harmonies being
played in a random order for an audience in a Turing
test or Imitation Game (Turing, 1950), attempting to
decide between human and computer generations.
In conclusion we believe that this work, while
needing much improvement, has given us a very in-
teresting glance in how the solution space of these
composition is made and has shown that we can use
collaborative evolution to achieve speciation between
the voices.
REFERENCES
Ashlock, D. and McEachern, A. (2011). A simulation
of bacterial communities. In 2011 IEEE Symposium
on Computational Intelligence in Bioinformatics and
Computational Biology, pages 61–68.
Boldrey, R. (1994). Guide to operatic roles & arias. Cald-
well Pub Co.
Brown, J. A. (2012). Multiple worlds model for motif dis-
covery. In 2012 IEEE Symposium on Computational
Intelligence in Bioinformatics and Computational Bi-
ology, pages 92–99.
Brown, J. A. (2013). More multiple worlds model for mo-
tif discovery. In 2013 IEEE Symposium on Compu-
tational Intelligence in Bioinformatics and Computa-
tional Biology, pages 168–175.
Brown, J. A. (2014). Regression and Classification from
Extinction. PhD thesis, University of Guelph.
Brown, J. A. and Ashlock, D. (2010). Using evolvable
regressors to partition data. In Inteligent Engineer-
ing Systems Through Artifical Neural Networks (20),
pages 187–194. AMSE Press.
Cope, D. (1991). Computers and musical style.
Dahlstedt, P. (2007). Autonomous evolution of complete pi-
ano pieces and performances. In Proceedings of Music
AL Workshop. Citeseer.
De Haas, B., Veltkamp, R. C., and Wiering, F. (2008). Tonal
pitch step distance: a similarity measure for chord
progressions. In ISMIR, pages 51–56.
Ebcio
˘
glu, K. (1988). An expert system for harmonizing
four-part chorales. Computer Music Journal, pages
43–51.
Grant, B. R. and Grant, P. R. (1979). The feeding ecology
of darwin’s ground finches. Noticias de Gal
´
apogos,
pages 14–18.
Grant, B. R. and Grant, P. R. (1982). Niche shifts and com-
petition in darwin’s finches: Geospiza conirostris and
Congeners. Evolution, 36:637–657.
Grant, B. R. and Grant, P. R. (1983). Fission and fusion
in a population of darwin’s finches: An example of
the value of studying individuals in ecology. Oikos,
41:530–547.
Hanson, T. (2011). Feathers: The Evolution of a Natural
Miracle. Basic Books.
Hoover, A. K., Szerlip, P. A., and Stanley, K. O. (2011).
Generating musical accompaniment through func-
tional scaffolding. In Proceedings of the Eighth Sound
and Music Computing Conference (SMC 2011).
Lack, D. (1947). Darwin’s Finches. Cambridge University
Press.
McKinney, J. C. (1982). The diagnosis & correction of vo-
cal faults. Broadman Press Nashville, Tennessee.
Miller, B. L. and Goldberg, D. E. (1995). Genetic algo-
rithms, tournament selection, and the effects of noise.
Complex Systems, 9(3):193–212.
Miranda, E. R. (2003). On the evolution of music in a soci-
ety of self-taught digital creatures. Digital Creativity,
14(1):29–42.
Miranda, E. R. (2013). Readings in music and artificial
intelligence. Routledge.
Schoenberg, A. (1978). Theory of harmony. Univ of Cali-
fornia Press.
Sessions, R. (1951). Harmonic practice. Harcourt, Brace.
Sulloway, F. J. (1982). Darwin and his finches : The evo-
lution of a legend. Journal of the History of Biology,
15(1):1–53.
Tilman, D. and Snell-Rood, E. C. (2014). Diversity breeds
complementarity. Nature, 515(7525):44–45.
Turing, A. M. (1950). Computing machinery and intelli-
gence. Mind, (49):433–460.
Whitley, W. D., Rana, S. B., and Heckendorn, R. B. (1997).
Island model genetic algorithms and linearly separa-
ble problems. In Selected Papers from AISB Workshop
on Evolutionary Computing, pages 109–125, London,
UK. Springer-Verlag.
Yi, L. and Goldsmith, J. (2007). Automatic generation of
four-part harmony. In BMA. Citeseer.
Zuppinger-Dingley, D., Schimd, B., Petermann, J. S.,
Yadav, V., Deyn, G. B. D., and Flynn, D. F. B.
(2014). Selection for niche differentiation in plant
communities increases biodiversity effects. Nature,
515(7525):108–111.
Evolving Four Part Harmony using a Multiple Worlds Model
227
