Real-Time Prediction to Support Decision-making in Soccer
Yasuo Saito
1
, Masaomi Kimura
2
and Satoshi Ishizaki
3
1
Division of Electrical Engineering and Computer Science, Shibaura Institute of Technology, Tokyo, Japan
2
Department of Information Science and Engineering, Shibaura Institute of Technology, Tokyo, Japan
3
Health and Physical Education, Shibaura Institute of Technology, Saitama, Japan
Keywords:
Soccer, Sports Data, Game Prediction, k-NN, Clustering.
Abstract:
Data analysis in sports has been developing for many years. However, to date, a system that provides tactical
prediction in real time and promotes ideas for increasing the chance of winning has not been reported in the
literature. Especially, in soccer, components of plays and games are more complicated than in other sports.
This study proposes a method to predict the course of a game and create a strategy for the second half. First, we
summarize other studies and propose our method. Then, data are collected using the proposed system. From
past games, games to similar to a target game are extracted depending on data from their first half. Next, similar
games are classified by features depending on data of their second half. Finally, a target game is predicted and
tactical ideas are derived. The practicability of the method is demonstrated through experiments. However,
further improvements such as increasing the number of past games and types of data are still required.
1 INTRODUCTION
Data analysis is becoming more common, including
in sports. Using data analysis results has become
familiar in sports organizations such as the Grand
Slam of the International Tennis Federation and Ma-
jor League Baseball in the USA.
Data analyses have also become popular in soc-
cer. Traditionally, in soccer, analyses were applied to
the numbers related to goals and shots. However, Shi-
genaga et al.(Shigenaga et al., 2014) used pass data,
because the number of passes is much greater than
that of goals and shots, and it provides more informa-
tion regarding the relative statuses of teams in a game.
Regarding players as nodes and passes as edges, the
motion of the ball creates a network. Shigenaga et al.
analyzed the network using graph theory and calcu-
lated centralities such as betweenness and closeness.
They determined the differences in pass networks be-
tween higher and lower ranked teams and between op-
ponents that tend to defeat a target team. From these
differences, they acquired strategies suitable for the
target team to defeat the opponent.
In fact, such analyses (Jo et al., 2014) (Yamada
et al., 2014) (Yamamoto and Yokoyama, 2011) are not
used to decide a strategy in real games. One reason is
that the motion of players and the ball is too compli-
cated to obtain data about every action that occurs in
the game. Another reason is that, since data analyses
are performed after the game, it is impossible to uti-
lize the acquired knowledge to provide advantages to
the team in the same game. Many situations such as
the conditions of players and constitutions of squads
in the team and its opponents can change every game.
This means that the most reliable data that we can use
in a game are those taken from that very game. In
fact, the number of passes and shots, percentage of
ball possessions, and covered distance of each player
are insufficient to express situations in soccer games.
Therefore, it is necessary to define new data suitable
for a useful analysis.
In this study, we propose a data schema for data
necessary to measure similarity between games, and
also propose a method to predict which strategy the
target team used in past game would be expected a
good result in the target game. This can be effective
way to support decision-making regarding strategy.
Our approach is based on the assumption that games
similar in the first half are also played similarly in the
second half. Accordingly, by applying memory-based
reasoning, we extract games similar to the target game
in the first half at the beginning of the method. If sim-
ilar games exist, it is expected that they are ether win-
ning, drawing or losing games. If the similar games
include many winning games, their features provide
the important knowledge for decision-making in the
218
Saito, Y., Kimura, M. and Ishizaki, S..
Real-Time Prediction to Support Decision-making in Soccer.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 1: KDIR, pages 218-225
ISBN: 978-989-758-158-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

target game. Even if there are only losing games in
the similar games, their feature of their games can be
useful to avoid losing in the target game. We apply
a clustering technique to classify similar games de-
pending on their features in the second half. Next, we
extract features of each groups (especially winning
game groups) by identifying data whose variance is a
minimum. Finally, we interpret the obtained features
in the games similar to the target game and predict
how the target game changes in the second half.
2 PROPOSED METHOD
2.1 Target Data
Our target data in this approach are the zone data.
Figure 1 illustrates an image of the pitch, which is
divided into 24 parts, divided longitudinally by six
and transversally by four. The transverse division was
defined to divide inside and outside the width of the
penalty box and on the left/right sides. At the World
Cup in Brazil last year, all 171 goal scorings at the
competition were made inside the width of the penalty
box. This suggests that there is a huge difference re-
garding the roles of the offense and defense depend-
ing on whether it was inside or outside the box. For
the longitudinal division, we expected to obtain infor-
mation such as efficiency of the attack from the ten-
dency of the longitudinal position where the ball was
frequently located.
Figure 1: Image of the pitch.
The zone data including three data types are as
follows:
• Ball Zone data (BZD)
The number of times players in a team handle with
the ball at each zone.
• Ball Interception data (BID)
The number of times players take over the ball
from their opponent players at each zone.
• Foul data (FD)
The number of times the players commit fouls at
each zone.
Moreover, we use the following statistical data
provided by Data Stadium Inc. (Data Stadium Inc.),
which handles J-League data.
• Chance percentage (the number of shots / the
number of attacks)
• Ball possessions per 15 min
• The number of shots per 15 min
• The success rate of Shot/Pass/Crosse/Take-
on/Tackle
2.2 Method
Figure 2 shows the broad outline of the technique.
The following describes each step of our method
Step 1: In this step, data are gathered by hand with
PileZD, a data input system developed by authors in
this study. Figure 3 shows its input screen. As we
showed in Section 2.1 , we use BZD, BID and FD as
original data in this method. Therefore, a user input
the type of each action that occurred in the game, such
as ball motion, ball interception and foul. Moreover,
it is also important that the position on the pitch where
each action occurred because even the type of actions
are same, they have different meanings according to
the position they happen. Therefore, it is essential
to get not only the type of action but position data.
For that reason, we developed that system to gather
data of ball motion, ball interception and foul in ev-
ery zone in the pitch as we showed in Figure 1. All
actions are able to be input their type of actions by
keyboard inputting, their zone where each actions oc-
curred by mouse clicking on the pitch in the input
screen(Figure 3). Furthermore, these data that gath-
ered with PileZD are compiled every 15 minutes and
stored into the database because it enable to reveal the
changes of the game flow based on temporal game de-
velopment.
Figure 2: Outline of the process.
Real-Time Prediction to Support Decision-making in Soccer
219

Figure 3: Input window of PileZD.
Step 2: In this method, we assume that games sim-
ilar in the first half are also similar in the second half,
because we empirically know that opponent teams
follow a pattern in their strategies toward the target
team. Under this assumption, past games similar to
the game in progress are extracted using zone data
such as BZD, BID and FD in the first half. Therefore,
extracted similar games will be similar to the target
game from viewpoints of ball motion, places where
the team gains/loses the ball and places the team gets
fouls.
The similarity of games is measured using the dis-
tance (Gordon S. Linoff, 1999) between vector data of
Figure 4: Creating subvectors.
Figure 5: Calculation for extraction.
game in progress and of each past game.
Figures 4 and 5 show how the distance means are
calculated. First, we create a set of subvectors of
BZD, BID, and FD for each home and away team,
as is shown in Figure 4. These subvectors have 24
elements regarding data of each zone. Then, we cre-
ate vectors by lining up each subvector in order. The
vectors v
ZD1
, v
ZD2
, and v
ZD3
in Figure 5 corresponds
to data in 0–15, 15–30, and 30 min at the end of the
first half, respectively. All vectors have 72 elements,
which are grouped into subvectors. BZD of the home
team: e
ZD1
, BID of the home team: e
ZD2
, FD of the
home team: e
ZD2
, BZD of the away team: e
ZD6
, BID
of the away team: e
ZD6
, and FD of the away team:
e
ZD6
. The vectors v
ZD1
, v
ZD2
, and v
ZD3
are created
separately for the first halves of a target game and the
past games and are used to calculate the Euclidean
distance between them. Let d
i
denote the distance be-
tween v
ZDi
and v
0
ZDi
(i = 1, 2, 3) and let the distance
of the game D
k−NN
be defined as their weighted sum:
D
k−NN
= 0.2 d
1
+ 0.4 d
2
+ 0.4 d
3
. We use less weight
for the first 15 min than the others because it is not
likely that characteristic features will appear in the
first 15 min. Applying k-NN method to the obtained
distances, the nearest k games are extracted as similar
games.
Step 3: In this step, we use a clustering algorithm
to divide similar games into multiple groups. Figure 6
shows how to calculate distances for clustering. Two
types of vectors are used: stats data vectors and zone
data vectors. Stats data vectors have 24 elements,
whose first 12 elements, denoted as e
SD1
in Figure 6,
are the stats data for the home team, and the second
12 elements, denoted as e
SD2
are the data for the away
team. If V
s
and V
0
s
are vectors of any two games cho-
sen from the similar games extracted in Step 2, their
Euclidean distance d
4
= |V
SD
−V
0
SD
| can be obtained
as
d
4
=
q
|e
SD1
− e
0
SD1
|
2
+ |e
SD2
− e
0
SD2
|
2
. (1)
Since this is a combination of stats data distances for
both teams, we adopt it as the distance between the
stats data in the second half of the game.
Here, zone data vectors are used to numerically
express the behavior of a ball in the game, whose def-
inition is the same as that in Step 2. However, in this
step, we use only one zone data vector, whose ele-
ments are the number counted in the entire of the sec-
ond half not every 15 min, as in Step 2. In our study,
we use the Euclidean distance d
5
between two zone
data vectors to measure their dissimilarities.
Finally, D
clustering
is the total distance between any
two games obtained in Step 2 and is calculated as the
sum of d
4
and d
5
.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
220

Figure 6: Calculation for clustering.
Figure 7: Example of a distance matrix.
Figure 7 is an example of a distance matrix be-
tween any two similar games. After creating this ma-
trix, to classify the games, we apply hierarchical clus-
tering (Toyoda, 2008) with Ward’s method (Toyoda,
2008) and obtain a dendrogram, as shown in Figure
8. Since the similar games can be divided into plural
groups, we chose hierarchical clustering as clustering
method to determine clusters based on the shape of
the dendrogram. In the next step, analysis of this den-
drogram reveals the features of each cluster.
Figure 8: Dendrogram.
Step 4: A threshold for dividing dendrograms into
plural clusters is determined in this step. Figure 8 is a
dendrogram based on the distance matrix in Figure7.
If it is split at the height as shown in Figure 8, all sim-
ilar games are divided into two parts: one group in-
cludes F, G, B, and H and the other group includes D,
C, A, and E. The height represents a distance thresh-
old for dividing the clusters.
After dividing similar games, we find features of
each group according to variances of parameters such
as BZD, BID and FD in their second half. Equation
2 is the variance used in this technique, where V is
the variance of one parameter, x
i
is the value of the
parameter of Game i, ¯x is the average value of the pa-
rameters, and N is the number of games.
V =
∑
N
i=1
(x
i
− ¯x)
2
N − 1
. (2)
Data of each parameter for all similar games are
normalized by subtracting their mean value and di-
viding by their variance (Toyoda, 2008). For each pa-
rameter, the variance is calculated, and when some
parameter has the lowest value of variance in the pa-
rameters, it is regarded as feature of the cluster. This
is because similar games in the same cluster have
close values of parameters. We take the mean value
for the parameter and interpret it by comparing with
other clusters. In this study, we employed three pa-
rameters that have the lowest variance.
3 EVALUATION
3.1 Objective and Method
The objective of this experiment is to evaluate the
proposed method by applying it to realistic data. To
simulate our method, we used 25 past J-League offi-
cial matches that Urawa Reds played in Seasons 2013
and 2014. We changed the target game and conducted
an experiment three times. Three randomly selected
games were used as target games and the other 22
games were used as past games. Before the exper-
iment, we collected BZD, BID, and FD data in the
first and second halves and statistical data in the sec-
ond half. In these experiments, as the past games in
the first half, we extracted eight similar games. After
the application, we calculated the winning percentage
for every cluster, discriminated which group was the
most superior, and used it to identify features that are
effective for playing the game advantageously.
On the basis of the experimental results, we dis-
cuss
• whether we can identify features that are effective
for playing the game advantageously,
• whether the actual results of the target game were
as predicted by our method.
We show the results of the experiment, in which
we used a J-League official game held on March 17th
2014, with Urawa Reds playing against Cerezo Os-
aka. In this game, Urawa Reds beat Cerezo Osaka by
a goal scored in the second half. We focus on whether
Urawa Reds won or lost in this section.
Real-Time Prediction to Support Decision-making in Soccer
221
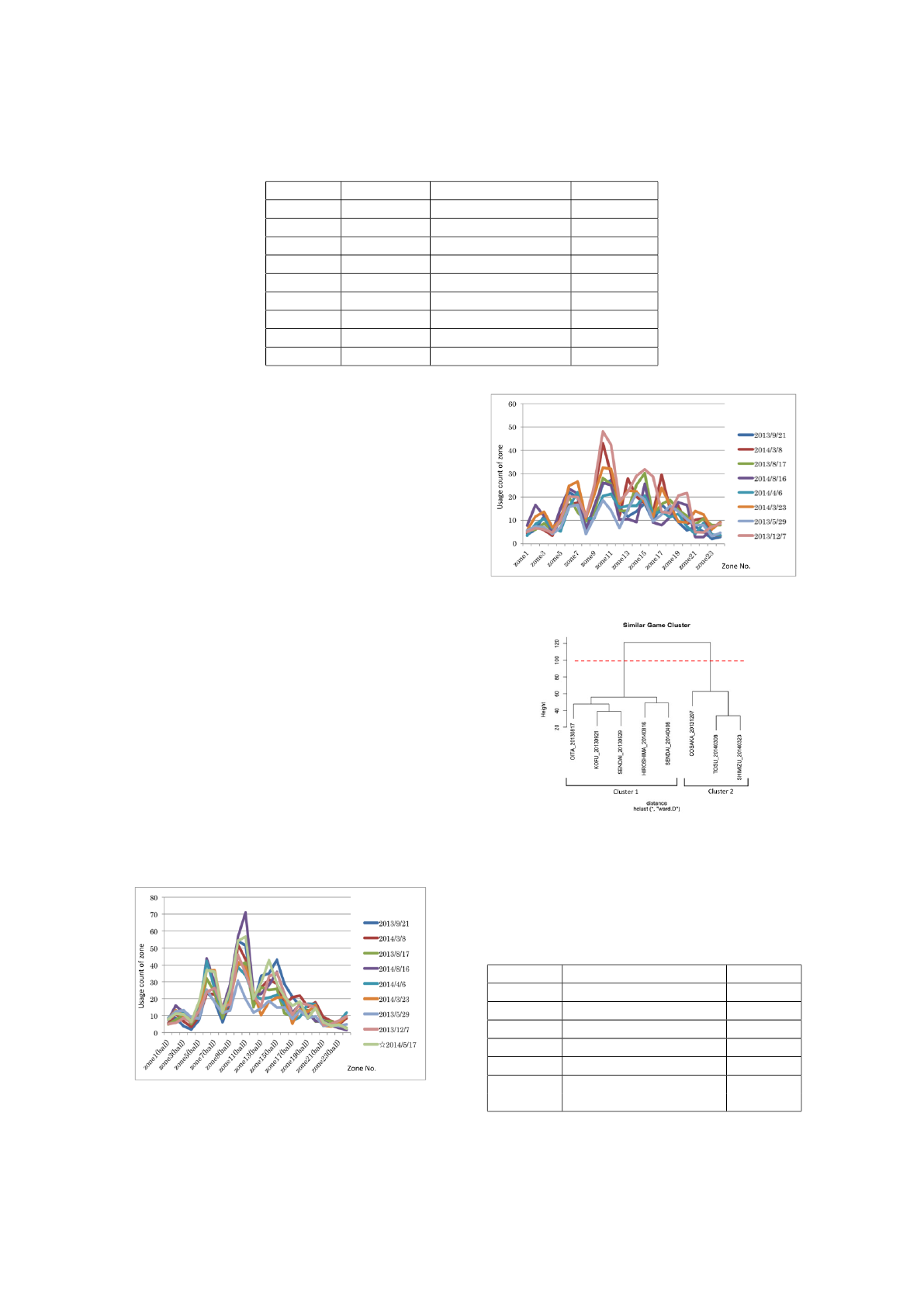
Table 1: Target game and similar games.
Distance Date Opponent teams Final score
0 (target) 2014/05/17 Cerezo Osaka 1 - 0
11.52 2013/09/21 Ventforet Kofu 1 - 1
11.91 2014/03/08 Sagan Tosu 0 - 1
13.07 2013/08/17 Oita Trinita 4 - 3
13.58 2014/08/16 Sanfrecce Hirosima 1 - 0
14.86 2014/04/06 Vegalta Sendai 4 - 0
14.88 2014/03/23 Shimizu S-Pulse 1 - 1
14.96 2013/05/29 Vegalta Sendai 1 - 1
15.03 2013/12/07 Cerezo Osaka 2 - 5
3.2 Result and Discussion
Table 1 shows the list of the target games and similar
eight games. Moreover, Figure 9 shows Urawa Reds’
BZD for every zone on the pitch in the first half of the
target game and similar games. The horizontal axis
indicates the zone number, and the vertical axis shows
the number of times the ball was placed at the zone.
Clearly, all lines in the graph have nearly the same
shape. This indicates that the target game and similar
games have some common points in how frequently
players in Urawa Reds used zones to bring the ball.
Figure 10 shows BZDs at every zone on the pitch
in the second half of the similar games. We can see
that all the lines in the graph are similar in shape. This
indicates that the games similar in the first half pro-
ceed similarly in the second half as well, at least in
terms of the motion of the ball. This suggests that
attacks against the same team tend to be similar re-
gardless of whether it is in the first or second half.
We then applied cluster analysis to these similar
games and obtained the dendrogram shown in Fig-
ure 11. If we set the threshold at more than 60, we
can divide the eight similar games into two clusters,
Cluster 1 with five games and Cluster 2 with three re-
maining games. Moreover, Table 2 shows the record
difference between the two clusters. In the J-League,
Figure 9: BZD in the first half of the target game and similar
games.
Figure 10: BZD in the second half of similar games.
Figure 11: Dendrogram of the Cluster Analysis.
a team gains three points by winning, one point by
drawing, and 0 points by losing. The index Points per
game in the table denotes the average of the points
that Urawa Reds gained in each cluster.
Table 2: Record differences between two clusters.
Cluster 1 Cluster 2
5 the number of games 3
3 - 0 - 2 Win - Draw - Lose 0 - 2 - 1
60% Winning Percentage 0%
2.2 Points per Game 0.333
8 Goal For in second half 2
2 Goal Against 3
in second half
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
222

From Table 2, Cluster 1 can be regarded as the
cluster of the games that Urawa Reds won, because,
e.g., the winning percentage in Cluster 1 is much
greater than that in Cluster 2. This shows that we
could classify the games similar to the target game
into two clusters showing different performances. It
also suggests that we suitably selected the parameters
used in the classification. It is important to investigate
the features of the Cluster 1 according to these ideas.
Table 3: Three lowest variances in Urawa Reds’ data in
Cluster 1.
Zone No. variance average
Zone 16 0.046 10.76
Zone 13 0.116 13.48
Zone 9 0.191 13.06
Table 3 shows three zones (or parameters in our
study) which that have the lowest variances even
though we used BZD as well as other parameters.
Consequently, we focus especially on the BZD of
games in Cluster 1.
To analyze how players in Urawa Reds used each
zone for their offense, averages of BZD for each zone
are shown in their corresponding portions of the im-
age of the pitch (Figure12). Moreover, variances of
each vertical four zones are calculated and shown un-
der the pitch to find the difference of usage in the cen-
ter and side areas. The three zones colored orange are
those with the smallest variances.
First, let us compare the data of Zones 9–16 (mid-
dle third) and Zones 17–24 (attacking third).
We can see that there are large differences in the
tendency of mean values between the middle third and
the attacking third. In the middle third, the mean val-
ues of center zones such as Zones 10, 11, 14, and 15
are clearly greater than those of outside zones, and
there are no large differences between center and out-
side areas in the attacking third. This means that in
the Cluster 1 games, Urawa Reds began their attack at
the center of the middle third, and they used the pitch
more widely toward the goal. In fact, in the game
on April 6 in 2014 between Urawa Reds and Vegalta
Sendai, all three goals that Urawa Reds scored in the
second half were the result of attacks that used both
the center and side areas in the pitch.
Similarly, by examining the mean value distribu-
tion of Cluster 2 (Figure13), we found the difference
of how Urawa Reds used the center zone and outside
of the pitch. Zones in the middle third, especially
Zones 13, 14, 15, 16, do not have clear differences
in the mean values in the center and outside. How-
ever, in the attacking third, there are large differences
in the mean value of each zone. Another point is that
Figure 12: Mean value of BZD of Cluster 1.
in the attacking third, the mean values of the left side
of the pitch (Zone 17, 21) are clearly higher than the
other area, suggesting that it is not desirable to use the
outside area unevenly in an attack.
From these results, we quantitatively confirmed
that it is important to use the pitch widely and equally,
especially in front of the opponents’ goal, because
Urawa Reds played advantageously in the second half
of the target game.
Figure 13: Mean value of BZD of Cluster 2.
Figure 14: Comparison of BZD.
Finally, we compared the features of the target
game and the games in Clusters 1 and 2. Figure
14 shows the mean value of each zone. The hori-
zontal axis indicates zone numbers and the vertical
axis shows usage counts. There are three lines in the
graph: blue, red, and green lines represent Clusters 1,
Cluster 2, and the target game, respectively. We can
Real-Time Prediction to Support Decision-making in Soccer
223
see that the green line is closer to Cluster 2, which has
a lower winning percentage than Cluster 1, although
Urawa Reds finally won the target game. This might
make us think that the result of our experiment is not
as expected.
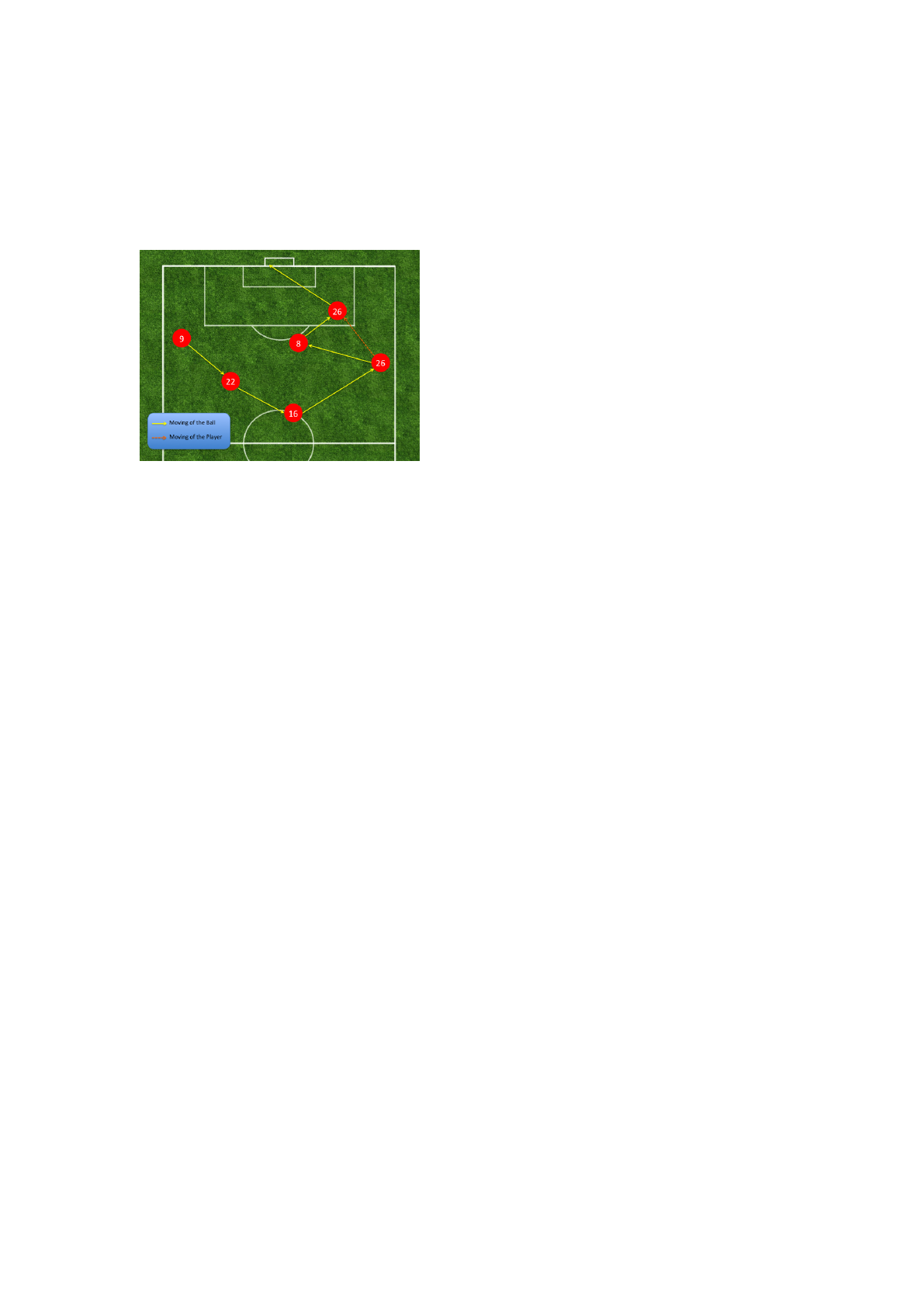
Figure 15: Goal process in the target game.
However, there were some effective attacks by
Urawa Reds in the second half of the target game.
Figure 15 shows the process of the goal that Urawa
Reds scored. It reveals that Urawa Reds used the
pitch widely, left-side, right-side, and center, a fea-
ture of attacks in Cluster 1. The reason why this oc-
cured is possibility that the distance between the sim-
ilar games and Claster 1 was wrongly calculated to be
long according to the parameters other than the scor-
ing and the used zones. Thus, in the future work, we
will need to define a distance that gives weight to the
parameters which are the features of obtained clus-
ters.
4 CONCLUSION
Recently, data analysis in sports has been developed.
Some systems have already been used to manage and
analyze data in several fields. However, so far, no
analysis method has been applied to soccer games. In
our study, we proposed a method for predicting how
games proceed in the real time.
To this end, we collected zone data (BZD, BID,
and FD) and statistical data of past games. During the
first half of the target game, zone data were collected
and used to extract similar games from past games.
Subsequently, the extracted similar games were clas-
sified by applying a clustering technique to data of
their second halves. This is because effective features
of similar games played well must also be effective in
the target game. Finally, features in the second half
in the clusters were extracted as the parameter having
the lowest variance. The information obtained was
used to discuss the strategy by which the team should
play advantageously in the second half of the target
game.
We evaluated our method by applying it to real
match data and established some points. First, we
confirmed that the method extracted games similar
to the target game. Moreover, these similar games
had similar features of zone data even in their sec-
ond halves. This means that we correctly assumed
that games with similar features in their first halves
will proceed similarly in their second halves. We
succeeded in extracting eight games from 22 past
games similar to the target game. A clustering tech-
nique revealed the difference in winning percentage
between clusters, showing that the parameters we
chose were suitable. Finally, the feature difference
between clusters that have higher and lower winning
rates were found to be closely related to strategies
that should be taken in the second half of the target
game. Though the strategy obtained was not epoch-
making, we quantitatively demonstrated an advanta-
geous strategy that is well known to people who often
watch soccer games.
In the future, we will increase the number of past
games to ensure a variety of games. In this study,
we used only zone data and a few types of statistical
data for clustering. More types of data must be used
for further analyses. Moreover, we will also need to
define a distance that gives weight to the parameters
which are the features of obtained clusters.
ACKNOWLEDGEMENTS
I wish to thank Data Stadium Inc. for providing J-
League data used in this study.
REFERENCES
Data stadium inc. https://www.datastadium.co.jp. [Online;
accessed 26-August-2015].
Gordon S. Linoff, . M. J. B. (1999). Data Mining Tech-
niques: For Marketing, Sales, and Customer Relation-
ship Management. Kaibun-do, 1st edition.
Jo, H., Yokoo, T., Ando, K., Nishijima, N., Kumagai, S.,
Naomoto, H., Suzuki, K., Yamada, Y., Nakano, T.,
and Saito, K. (2014). The attacking indexes of play-
ers and teams in j league. In Research on Sports Data
Analysis, volume 1, pages 21 – 26. The Institute of
Statistical Mathematics.
Shigenaga, K., Nakatsu, T., Naito, T., Kata, T., Saruta, S.,
Hidaka, A., Enomoto, D., Ogura, T., and Kamakura,
M. (2014). The pass analysis in soccer based on graph
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
224
theory. In Research on Sports Data Analysis, vol-
ume 1, pages 15 – 20. The Institute of Statistical Math-
ematics.
Toyoda, H. (2008). The Guide to Data Mining with R. Toky-
oTosyo Co.,Ltd.
Yamada, M., Yagi, K., Munakata, S., Hunayama, T., and
Yamamoto, Y. (2014). The visualization of zone us-
age in soccer. In Research on Sports Data Analysis,
volume 1, pages 45 – 50. The Institute of Statistical
Mathematics.
Yamamoto, Y. and Yokoyama, K. (2011). Common and
unique network dynamics in football games. In PLos
ONE, volume 6.
Real-Time Prediction to Support Decision-making in Soccer
225
