GPGPU Vs Multiprocessor SPSO Implementations to Solve
Electromagnetic Optimization Problems
Anton Duca
1
, Laurentiu Duca
2
, Gabriela Ciuprina
1
and Daniel Ioan
1
1
Politehnica University of Bucharest, Faculty of Electrical Engineering, Bucharest, Romania
2
Politehnica University of Bucharest, Faculty of Computer Science, Bucharest, Romania
Keywords: SPSO, GPGPU, Pthreads, Electromagnetic Field, Optimization.
Abstract: This paper studies two parallelization techniques for the implementation of a SPSO algorithm applied to
optimize electromagnetic field devices, GPGPU and Pthreads for multiprocessor architectures. The GPGPU
and Pthreads implementations are compared in terms of solution quality and speed up. The electromagnetic
optimization problems chosen for testing the efficiency of the parallelization techniques are the TEAM22
benchmark problem and Loney’s solenoid problem. As we will show, there is no single best parallel
implementation strategy since the performances depend on the optimization function.
1 INTRODUCTION
Electromagnetic optimizations are problems in
which the objective function has a high degree of
complexity, because the electromagnetic field
equations are solved for its evaluation. This function
is usually a multidimensional one, with multiple
local minimum, difficult constraints to be observed,
defined on a large search space. That is why the
evaluation of such an objective function is often
very computational intensive, needing a large
number of instructions, with high branching level,
sometimes using recursive calls (Takagi and
Fukutomi, 2001) (Duca et al., 2014) . Moreover, the
evaluation is often poorly conditioned and therefore
it is noise sensitive (Takagi and Fukutomi, 2001).
Since deterministic methods such as the steepest
descent method, or conjugate gradient method can
not be applied because of many local minimum of
the objective function, in recent decades heuristics
based on tabu search, simulated annealing, genetic
algorithms, particle swarm optimization, etc, were
imposed as standard techniques for solving
electromagnetic optimization problems (Duca et al.,
2014) (Li et al, 2004). The main advantages of these
stochastic methods are robustness and their ability to
find the global minimum of the objective functions
without knowing their derivatives. The main
disadvantage of these methods, important for real
life problems for which the objective function
evaluation cost is high, is the significant number of
objective function evaluations.
To reduce the solving time the following
solutions are used: reducing the number of
evaluations of the objective function by improving
the stochastic optimization method (Ciuprina et al.,
2002) (Ioan et al., 1999), implementation of parallel
/ distributed architectures for the optimization
algorithm (Duca and Tomescu, 2006), decrease the
evaluation time for the objective function using
more efficient problem specific methods (Chen et
al., 2006).
The purpose of this paper is to investigate and
compare two parallelization techniques, namely
GPGPU (General Purpose Computation on Graphics
Processing Units) and Pthreads (POSIX threads), for
reducing the solving time of some electromagnetic
optimization problems. To solve the electromagnetic
problems a parallel SPSO (Standard Particle Swarm
Optimization) algorithm is used. The parallel
implementations, one based on CUDA (Compute
Unified Device Architecture) language and one
based on Pthreads, first running on a GPU (Graphics
Processing Unit) while second running on a
multiprocessor architecture, are compared using as
criteria the solution fitness and the speed up for
different SPSO (Standard Particle Swarm
Optimization) swarm sizes. For testing and
comparing the parallelization techniques of the
SPSO algorithm the TEAM22 benchmark problem
(TEAM22, 2015) and Loney’s solenoid problem (Di
64
Duca, A., Duca, L., Ciuprina, G. and Ioan, D..
GPGPU Vs Multiprocessor SPSO Implementations to Solve Electromagnetic Optimization Problems.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 64-73
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Barba and Savini, 1995) were chosen as
optimization problems.
2 SPSO ALGORITHM
Initially proposed by Kennedy and Eberhart
(Kennedy and Eberhart, 1995), PSO (Particle Swarm
Optimization) is an iterative optimization algorithm
which has the roots in biology and is inspired from
the social behavior inside a bird flock or a fish
school. Each particle in the swarm is described by
position and velocity. The position encapsulates the
potential solution of the optimization problem (its
coordinates in the searching space) while the
velocity describes the way the position is modified.
At iteration (time) t + 1 the position x
i
and the
velocity v
i
of each particle i in the swarm are
computed as follows:
)1()()1(
tvtxtx
iii
,
(1)
)()(
)()1(
21,
txrwtxrw
tvwtv
GBGBiPBiPB
ivi
(2)
)()()( txtxtx
iiPBiPB
,
(3)
)()()( txtxtx
iGBGB
,
(4)
where x
PB
, x
GB
are the best personal position and the
best position in the group (swarm), w
v
, w
PB
, w
GB
are
the weights for velocity, “cognitive” term and
“social” term, and r
1
, r
2
two random numbers
distributed uniformly in the interval [0, 1). So the
time step is considered 1 and the velocity vector is
computed as a weighted average, assuring a random
but enough smooth movement of particles, attracted
to the best known position.
The main issues of the original PSO are the high
probability of being trapped in local minima and the
large number of objective function evaluations
needed to find the global solution. During time, for
improving the performance of the PSO different
approaches were proposed. Some of the most
efficient PSO based algorithms available today are
IPSO (Intelligent PSO) (Ciuprina et al., 2002),
SPSO (Standard PSO) (Bratton and Kennedy, 2007),
QPSO (Quantum-behaved PSO) (Sun et al., 2011)
and DPSO (Discrete PSO) (Pan et al., 2008).
Currently at its third version (Clerc, 2012), SPSO
modifies the classical algorithm in terms of
initialization, velocity / position update equations,
neighborhood and confinement. In the case of SPSO,
the particles of the swarm are connected, each
connection representing a link between two different
particles. A connection has an informed and an
informing particle, the first particle knowing the
personal best and the position of the second particle.
Thus, each informed particle has a set of informing
particles called neighborhood. SPSO uses a random
topology which changes the connections graph at
each unsuccessful iteration (when the global best
solution is not improved).
The initializations for position and velocity are
made to avoid leaving the search area, especially
when the optimization variables number is high. The
position coordinates are generated randomly for
each direction (d) using a uniform distribution, while
the velocity coordinates are generated taken into
consideration the generated position coordinates:
)max,min()0(
ddi
Ux
,
(5)
))0(max),0((min)0(
,, diddidi
xxUv
.
(6)
The velocity formula introduces a new term, the
center of gravity, for obtaining “exploration” and
“exploitation”. The center of gravity depends on
three terms: the current position, a term relative to
the previous best x
PB,i
, and a term relative to the
previous best in the neighborhood x
LB,i
. Thus, the
update equations for velocity and positions are
changed comparing with the original PSO algorithm,
as follows:
)()()()1(
'
txtxtvwtv
iiii
,
(7)
)()()1()()1(
'
txtvwtvtxtx
iiiii
,
(8)
where x'
i
is a random point inside a hypersphere of
radius ||G
i
– x
i
|| and center G
i
, with G
i
being the
center of gravity for the particle i:
3
))(())((
iiLBiiiPBii
i
xxcxxxcxx
G
,
(9)
or if the particle i is the best particle in its
neighborhood (has the best fitness value):
2
))((
iiPBii
i
xxcxx
G
.
(10)
Another feature of the SPSO algorithm is the
confinement. If during the iterative process a particle
moves outside the search space on some coordinate
d, its velocity and position are modified as follows:
})(5.0)(;min)({
then)min)((if
,,,
,
tvtvtx
tx
dididdi
ddi
,
(11)
})(5.0)(;max)({
then)max)((if
,,,
,
tvtvtx
tx
dididdi
ddi
.
(12)
GPGPU Vs Multiprocessor SPSO Implementations to Solve Electromagnetic Optimization Problems
65
The main disadvantage of stochastic methods is
the large number of objective function evaluations,
especially in real problems when the objective
function evaluation cost is significant. In this case,
the solving time for the sequential implementations
is significat, the need for a parallel optimization
algorithm being obvious.
3 SPSO PARALLELIZATION –
GPGPU APPROACH
Due to market demand for high-definition 3D
graphics, and realtime processing, the GPU evolved
into a parallel, multithreaded, and manycore
processor with high computational power and
memory bandwidth (Nvidia CUDA, 2015). If a CPU
focuses on flow control and data caching, a GPU is
designed for parallel computational applications,
like graphics rendering, and is suitable for problems
where the same program is run in parallel on many
and different sets of data. In order to use the GPU
for general purpose computation and to solve
complex computational problems from different and
various domains (not only graphics rendering)
several programming models such as CUDA and
OpenCL have been created.
3.1 Existing Approaches
The idea of using implementations based on GPGPU
for PSO is not new. In (Zhou, Tan, 2009) GPGPU
implementation of SPSO 2007 showed acceleration
up to 11 times compared with traditional CPU
implementations.
In (Mussi, Cagnoni, 2009) the authors focus on
the data representation in memory (especially on the
best global position / local) such that reading /
writing operations to be carried out effectively. The
obtained acceleration was up to 100 times
comparing to the sequential CPU implementation,
for a problem with 100 variables and PSO
algorithms with 3 sub-swarms.
In (Mussi et al., 2009) and (Bastos-Filho et al.,
2010) the authors study the results quality of the
GPGPU implementations depending on where the
random numbers are generated (CPU or GPU). Both
studies suggest ways of generating random numbers
on the GPU, the results having a good quality.
In (Solomon et al., 2011) the authors study the
parallelization of a multi-swarm PSO algorithm to
solve combinatorial problems such as the allocation
of tasks. Again, it was observed that the GPGPU
implementation led to an acceleration of 37 times
compared with the sequential version of the
algorithm, especially for large problems.
In (Hung and Wang, 2011) a multi-objective
PSO version which uses one subswarm for each
objective is parallelized. The GPGPU
implementation performed 3 to 7 times faster than
CPU implementation.
Other GPGPU implementations of the PSO
based algorithms are proposed in (Castro-Liera et
al., 2011) and (Mussi et al., 2011).
Most of the proposed solutions are tested (like
many others) on functions with simple analytical
expressions (with many local minimum but not
computational intensive), and focus on the influence
over the performance of: the data transfer between
the host and the device (GPU), the manner and the
place of generating random values, the type of
implementation synchronous / asynchronous, etc.
Unfortunately the solutions do not address specific
aspects of the objective function implementation
such as the level of branching or the code
complexity.
3.2 Proposed CUDA Implementation
To implement the parallel version of the SPSO
algorithm the CUDA-C language was chosen.
Introduced by Nvidia, CUDA (Nvidia CUDA, 2015)
is a programming model a parallel computing
platform. The CUDA developer kit allows software
developers to create general purpose parallel
applications with languages such as Java, C++, C
Fortran and others.
Because of the hardware variety of the GPUs,
which can have a different stream multiprocessors
number, CUDA was built as a scalable software
programming model. Thus, a CUDA software
program can be executed (compiled) on any GPU
device independent of the multiprocessors number.
The CUDA programming model has as its core
the following three key concepts: a memory model,
synchronization mechanisms and a hierarchy of
thread blocks. These concepts help the developer to
split the task into smaller tasks which can be solved
separately by different blocks of threads. For solving
a task, the threads inside a CUDA program can work
independently or can cooperate.
In order to solve a problem the threads can use
barrier mechanisms to synchronize their execution.
These barrier mechanisms can only be used to
synchronize threads from the same block, and can
not synchronize blocks. To synchronize blocks the
software developer must split the program into
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
66
smaller sections and implement those with different
functions (kernels).
For implementing the SPSO parallel algorithm
with CUDA there are the following two possible
options: an implementation for configurations with
all threads in a single block (one thread block), or an
implementation for cases with multiple thread
blocks. In both implementations each thread
simulates a particle’s behavior and calls functions as
evaluation, movement, personal/local best
calculation, etc.
In first case, the SPSO parallel implementation is
done using one kernel. The synchronization between
particles (threads), necessary at certain steps, is
obtained using
__syncthreads function (a barrier
mechanism for synchronization). This strategy has
as main advantage the avoidance of kernels
relaunch. The disadvantages of this implementation
are: the maximum number of particles is 1024 (a
block may have at most 1024 threads), multiple
warps of threads (if the particles number exceeds the
warp size – 32), and threads branching possibility
(depending on the objective function).
For the second implementation, because the
barrier mechanism can not be used to synchronize
threads from different blocks, the particles
synchronization is realized by implementing each
function of a particle as a kernel. The main
disadvantage of this strategy is the delay because of
the kernels relaunch at each SPSO iteration.
Comparing with first implementation, the main
advantages are: the possibility to execute all threads
in parallel at the same time (for configurations with
one warp, maximum 32 threads in one block), and
the maximum particles number is not limited to
1024.
The parallel SPSO algorithm was implemented
using the strategy with multiple kernels (Duca et al.,
2014), and has the following main loop:
for(int i=0; i<SPSO_ITERATIONS; i++) {
moveParticles<<B,TpB>> (particles,
particleGB,varsMin,varsMax);
evaluate<<B,TpB>>(particles);
findGlobalBest<<B,TpB>>(particles,
particleGB, improvedGB);
generateTopology<<B,TpB>>(particles,
improvedGB);
findLocalBest<<B,TpB>>(particles);
}
where
B is the bocks number and TpB is the threads
number per block. The initialization, evaluation, ,
topology generation, personal / local and global best
calculation are performed before the main loop.
The kernels variables are global variables and
they are stored on the device (GPU). The
varMin,
varMax arrays contain the domain limits (minimum
and maximum values) for each search space
coordinate. The variable
improvedGB has a boolean
type and is used to decide if the swarm topology will
be changed (if the global best value is not improved
at a certain iteration the
generateTopology kernel
is called). The swarm particles are stored in the
particles variable, which is an array of type
Particle:
typedef struct {
double coords[PROBLEM_SIZE];
double fitnessValue;
double velocity[PROBLEM_SIZE];
double gravityCenter[PROBLEM_SIZE];
int indexLB;
int neighbours[PARTICLES_NUMBER];
} Particle;
The moveParticles function computes the
new particles positions, while the evaluate
function computes the fitness value, updates the
personal best (position and fitness value) for each
particle. The functions called inside evaluate
(
paramsCorrection, objectiveFunction,
findPersonalBest) are device functions which
have the __
device specifier. Each of these device
functions is executed in parallel (just like
evaluate) for all the swarm particles. The first
function checks the coordinates restrictions
(imposed by the problem) and, if is needed, changes
the particle’s coordinates to meet the constraints.
The second function, the optimization problem
(TEAM22 or Loney’s solenoid), has a sequential
implementation and computes the fitness value for a
particle.
__global__ void evaluate(Particle
*particles) {
int tid = blockIdx.x * blockDim.x +
+ threadIdx.x;
paramsCorrection(&particles[tid]);
particles[tid].fitnessValue =
objectiveFunction(particles[tid]);
findPersonalBest(particles);
}
The
findGlobalBest updates the best particle
of the swarm, and the
improvedGB variable (to true
or false if the fitness value for the best particle was
or was not improved at the current step). The
generateTopology creates a new topology (new
connections between the swarm particles) if the
global best value was not improved at the current
step. Based on the new topology, the
GPGPU Vs Multiprocessor SPSO Implementations to Solve Electromagnetic Optimization Problems
67
findLocalBest calculates the index of the local
best for the neighborhood of each particle. The
indexLB data field is then used to establish whether
the particle is the best particle in its neighborhood,
in order to choose the formula for determining the
new particle’s coordinates.
__global__ void findLocalBest(
Particle *particles){
int tid = blockIdx.x * blockDim.x +
+ threadIdx.x;
particles[tid].indexLB = tid;
for(int i=0;i<PARTICLES_NUMBER;i++) {
if(
particles[tid].neighbours[i] == 1
) {
if(
particles[i].fitnessValuePB
<
particles[
particles[tid].indexLB
].fitnessValuePB
) {
particles[tid].indexLB = i;
}
}
}
}
The implementation of the SPSO parallel version
using the single kernel strategy is similar; the kernel
functions have to be changed to device functions (by
simply replacing the __
global with the __device
specifier), while the main program loop has to be
coded as a kernel function, kernel\ which will be run
from the main program. The working threads have to
be explicitly synchronized after some calls of the
device functions using the __
syncthreads library
function.
4 SPSO PARALLELIZATION –
PTHREADS APPROACH
In shared memory multiprocessor architectures,
threads can be used to implement parallelism.
POSIX Threads (POSIX Threads, 2015), usually
referred as Pthreads, is a POSIX (Portable Operating
System Interface) standard for threads (POSIX
Threads standard, 2008) which defines an API
implemented on many Unix like operating systems
as Linux, Solaris, FreeBSD and MacOS.
In such operating systems, a process requires a
significant amount of overhead, containing
information about program resources and program
execution state: process ID, user ID, environment,
program instructions, registers, stack, heap, file
descriptors, signal actions, shared libraries, inter-
process communication tools (message queues,
pipes, semaphores and shared memory), etc.
Unlike a process, a thread is an independent
stream of instructions that can be scheduled to run
by the operating system. In a Unix environment, a
thread exists within a process, uses the process
resources, and has its own independent flow of
control. A thread duplicates only the essential
resources needed to be independently schedulable:
stack pointer, registers, scheduling properties (policy
and priority), and set of pending and blocked
signals. Because most of the overhead has already
been accomplished through the creation of its
process, a thread is lightweight when compared to
the cost of creating and managing a process, and can
be created with much less operating system
overhead. Therefore managing threads requires
fewer system resources than managing processes.
When running in shared-memory model, each
thread has access to its on private data but also has
access to the global (shared) memory. Because the
threads belonging to a process share their resources,
changes of global resources made by one thread will
be seen by all threads. This is why the read / write
operations to the same memory location require
explicit synchronization, synchronization which can
be implemented using mechanisms as barriers and
mutexes.
Comparing to other parallelization options for
multi-processor architecture with shared memory,
like MPI or OpenMP, Pthreads was created to
achieve optimum performance (POSIX Threads
tutorial, 2015). While MPI (MPI, 2015) and
OpenMP (OpenMP, 2015) are simpler parallelize-
tion options (easier to use) requiring a smaller
amount of work, Pthreads provides more flexibility
and it offers more control over the parallelization.
4.1 Existing Approaches
Just as in the CUDA case, there is a significant
number of PSO parallel implementations based on
the shared memory multiprocessor architectures.
While the optimization algorithms are used to solve
a variety of applications most of the programs are
based on MPI and OpenMP because of the
implementation simplicity (Wang et al., 2008)
(Zhao-Hua et al., 2014) (Han et al., 2013).
In (Tanji et al., 2011) the authors use a PSO
OpenMP implementation to design a class E
amplifier. The speed up obtained by parallelization
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
68
is up to 5 times. In (Thomas et al., 2013) a MPI
implementation is used for solving the optimum
capacity allocation of distributed generation units
and an 3 times acceleration is obtained comparing to
the serial implementation.
In (Roberge et al., 2013) the authors make a
comparison between a PSO CUDA implementation
and a PSO MPI implementation used to solve an
optimization problem from the area of power
electronics. Both implementations are faster than the
sequential PSO, the GPGPU CUDA implementation
being 32 times faster than the multiprocessor MPI
implementation.
In our opinion there is no single best parallel
implementation strategy for the PSO based
algorithms. As we will see from our simulations
results, the performances depend on many factors as
PSO parameters and especially the objective
function to be optimized and its implementation
features (like the code complexity and the level of
branching).
4.2 Proposed Pthreads Implementation
Just as in the CUDA implementation, in the Pthreads
case we implemented the behavior of each particle
in the swarm using a dedicated thread. The threads
management is done explicitly. The threads are
created and launched using
pthread_create
library function. The function receives as parameters
a reference to the thread, thread attributes (
NULL
means defaults are applied), the function to be
executed by the thread, and the thread ID:
pthread_t threads[PARTICLES_NUMBER];
int tid[PARTICLES_NUMBER];
...
for(int i = 0;i<PARTICLES_NUMBER;i++) {
tid[i] = i;
pthread_create(&threads[i], NULL,
&jobForOneThread, &tid[i]));
}
After creation, each thread executes the code
corresponding to the function
jobForOneThread.
The function contains the SPSO main loop and
performs the basic operations: particle movement
and evaluation, personal/global best calculation,
reset/generate new topology, and local best
calculation:
void* job_for_one_thread(void *params){
int tid = *((int*)params);
...
for(i=0;i<SPSO_ITERATIONS;i++) {
moveParticle(tid);
evaluateParticle(tid); barrier();
findGlobalBest(tid); barrier();
generateTopology(tid); barrier();
findLocalBest(tid); barrier();
}
...
}
The variable passed to the SPSO basic functions
is only the thread ID. The code of these functions is
the same as in the CUDA implementation. The
variables
varMin, varMax, improvedGB, particles
(which were passed as function parameters in the
CUDA implementation and were stored in the GPU
device memory) are now global variables stored in
the host computer memory, all threads having access
to them.
The particles synchronization (necessary after
each operation) is achieved using a barrier
mechanism based on the
pthread_barrier_wait
library function:
pthread_t void barrier() {
int rc = pthread_barrier_wait(&barr);
if(rc != 0 &&
rc != PTHREAD_BARRIER_SERIAL_THREAD
) {
printf("Can not wait on barrier!");
exit(-1);
}
}
The barr parameter is a variable of type
pthread_barrier_t which contains several data
members as the current number of threads reaching
the barrier, the size of the barrier (the necessary
number of threads to unlock the barrier), a mutex
(for exclusive access to data members), etc. The
variable is defined and initialized before the thread
creation and execution using the
pthread_barrier_init function:
// Barrier initialization -- before the
// thread creation loop
pthread_barrier_t barr;
if(
pthread_barrier_init(
&barr, NULL, PARTICLES_NUMBER)
) {
printf("Can not init barrier!");
exit(1);
}
5 ELECTROMAGNETIC
PROBLEMS
The parallel implementations were tested on two
benchmark problems defined by the computational
GPGPU Vs Multiprocessor SPSO Implementations to Solve Electromagnetic Optimization Problems
69
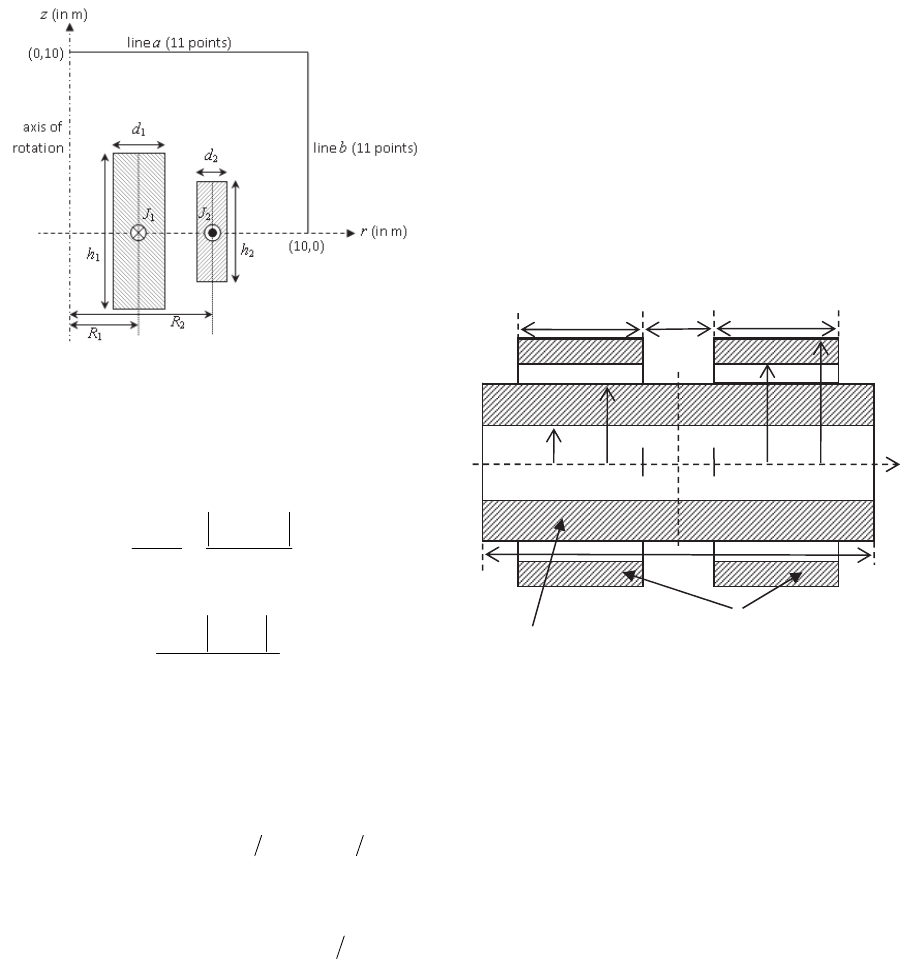
electromagnetics community.
5.1 The TEAM22 Benchmark Problem
Two coaxial coils carry current with opposite
directions (Figure 1), operate under superconducting
conditions and offer the opportunity to store a
significant amount of energy in their magnetic
fields, while keeping within certain limits the stray
field (Ioan et al., 1999).
Figure 1: TEAM22 problem configuration.
An optimal design of the device should therefore
couple the value of the energy E to be stored by the
system with a minimum stray field B
stray
. The two
objectives are combined into one objective function:
ref
ref
norm
stray
E
EE
B
B
OF
2
2
,
(13)
22
2
22
1
,
2
i
istray
stray
B
B
,
(14)
where E
ref
= 180 MJ, and B
norm
= 3 μT.
The objective function has as parameters, the
radii (R
1
, R
2
) , the heights (h
1
, h
2
) , the thicknesses
(d
1
, d
2
) and the current densities (J
1
, J
2
). Besides
domain restrictions, the problem must take into
account the following conditions: the solenoids do
not overlap each other (
22
2211
dRdR
), and
the superconducting material should not violate the
quench condition that links together the value of the
current density and the maximum value of magnetic
flux density (
2
mmA)0.54||4.6(|| BJ
). It
is a constrain imposed to the current densities.
The evaluation method of the objective function
is based on the Biot-Savart-Laplace formula in
which the elliptic integrals are computed by using
the King algorithm and numerical integration.
Moreover, the optimization problem is reformulated
as a one with six parameters, since for a given
geometry and a stored energy, the values of the
current densities can be computed by deterministic
quadratic optimization as in (TEAM22, 2015).
5.2 Loney’s Solenoid Problem
The Loney's solenoid benchmark problem,
formulated in (Di Barba et al., 1995) consists of a
main coil (Figure 2), with given dimensions (r
1
= 11
mm, r
2
= 29 mm, h = 120 mm ) and two identical
correction coils, having fixed radii (r
3
= 30 mm, r
4
=
36 mm). A constant current flows through the coils
such that they current density is the same. The aim is
to produce a constant magnetic flux density in the
middle of the main coil. The parameters to be
optimized are the length of the correction coils (s)
and the axial distance between them (l).
Figure 2: Loney’s solenoid problem configuration.
The objective function is of minmax type, i.e.
minimize the maximum difference between the
values of the magnetic flux density along a straight
segment in the middle of the main solenoid, i.e.
minimize (B
max
- B
min
)/B
0
, where B
0
is the magnetic
field density in the middle of the main coil (r=0,
z=0). The maximum and minimum values are sought
along the segment [-z
0
,z
0
], where z
0
= 2.5 mm. Tests
done by the authors of this benchmark revealed that
the problem is non convex and ill conditioned (Di
Barba and Savini, 1995). The electromagnetic field
problem is easily solved, in a magnetostatic regime,
by discretizing the coils in elementary coils without
thickness and by applying well known analytical
main coil correcting coils
-
z
0
z
0
r
1
r
2
r
3
r
4
s
l
s
h
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
70

formulas for the field along the solenoid axis.
6 RESULTS
To solve the electromagnetic optimization problems
two parallel SPSO implementations have been used,
a multiple kernel CUDA implementation and a
Pthreads implementation. In both implementations
one thread is mapped to one particle of the swarm.
The objective functions for the TEAM 22 and
Loney’s solenoid have sequential implementations
and they were written in C. For a given set of
parameters, the evaluation of one objective function
in case of TEAM22 problem consists in executing
tens of thousands of lines of code with a very high
level of branching, while in the case of Loney’s
solenoid one evaluation consists of hundreds lines of
code with a lower level of branching.
The CUDA SPSO code was tested on a NVIDIA
M2070 GPU with 448 cores, compute capability 2.0
and 1.13 GHz core processors. The Pthreads SPSO
code was tested on a multiprocessor hardware
architecture with two Intel Xeon X5650 CPUs (2.67
GHz), each processor with 6 cores and each core
being able to run in parallel 2 independent threads.
In total only 12 threads can run in parallel at a time
on the multiprocessor architecture, significantly
smaller than in the GPU case.
Tables 1 and 2 present the average execution
time for 30 independent runs (tests) for different
swarm sizes of the SPSO algorithm. For each run
(test) the stop criteria was the maximum iterations
number corresponding to 2560 evaluations of the
objective function.
Table 1: Average execution times for TEAM 22 problem.
Swarm
size
Algorithm
GPGPU – SPSO Pthreads – SPSO
32 327 s 19 s
64 198 s 17 s
128 144 s 15 s
For the TEAM 22 optimization problem the Pthreads
implementation is faster than the CUDA
implementation for each swarm size. The speed up
obtained for Pthreads with respect to GPGPU
implementation is from 9 times, in the case of 128
particles, to 17 times, in the case of 32 particles.
Even if in the CUDA case the number of threads
running in parallel in the same time is higher than in
the Pthreads case, the Pthreads implementation is
faster because of the complexity of the TEAM22
objective function implementation (high level of
branching and large number of instructions). The
main explanation is that the GPU cores have lower
clock rates, no branch prediction and no speculative
execution comparing with the multiprocessor cores.
Table 2: Average execution times for Loney’s solenoid
problem.
Swarm
size
Algorithm
GPGPU – SPSO Pthreads – SPSO
32 17 ms 71 ms
64 11 ms 79 ms
128 7.5 ms 82 ms
For the Loney’s solenoid problem the situation is
reversed, the CUDA implementation being the
fastest. The speedup for GPGPU with respect to
Pthreads implementation is from 4 times, when the
swarm has 32 particles, to 10 times, when the
number of particles is 128. The explanation once
again is related to the objective function
implementation, which in this case has a much lower
number of instructions and a lower branching level
comparing with the TEAM22 case. The advantages
of the multiprocessor architecture (the higher clock
rates, the bigger cache level, the branch prediction,
the speculative execution, etc) can not compensate
the disadvantage of the larger number of threads
running in parallel on the GPU architecture.
In terms of solution fitness (tables 3 and 4) the
results obtained with the parallel Pthreads
implementation are slightly better than those
obtained with the CUDA code, for both
electromagnetic optimization problems. For both
implementations the random numbers necessary for
the SPSO algorithm are generated at each step, on
host in the case of Pthreads and on device/GPU in
the case of CUDA.
For the Loney’s solenoid problem the best
performances are offered when the size of the swarm
Table 3: Objective function and standard deviation values
(× E–3) for TEAM 22.
Algorithm
GPGPU – SPSO Pthreads – SPSO
Swarm
size
32 64 128 32 64 128
Min -
best
3.15 3.53 3.37 3.06 3.34 3.75
Max –
best
17.40 11.30 9.11 8.46 8.09 12.24
Mean -
best
6.49 5.83 6.37 5.21 5.22 6.89
Standard
deviation
3.89 2.16 1.74 1.47 1.23 1.93
GPGPU Vs Multiprocessor SPSO Implementations to Solve Electromagnetic Optimization Problems
71

is small (32 particles), for both implementations. For
TEAM 22 benchmark problem the optimum swarm
size is between 32 and 64 when Pthreads
implementation is used, while for the CUDA
implementation it does not seem to be an optimal
size (32 offers best solution, 64 best mean, 128 best
standard deviation).
Table 4: Objective function and standard deviation values
(× E–3) for Loney’s solenoid.
Algorithm
GPGPU – SPSO Pthreads – SPSO
Swarm
size
32 64 128 32 64 128
Min -
best
1.31 1.51 1.49 1.25 1.31 1.34
Max –
best
1.61 2.07 6.61 1.59 2.44 18.63
Mean -
best
1.52 1.66 3.32 1.51 1.67 3.84
Standard
deviation
0.06 0.15 1.56 0.07 0.19 3.29
7 CONCLUSIONS
The current paper studied two parallelization
techniques, GPGPU and Pthreads, to speed up the
SPSO algorithm when solving electromagnetic
optimization problems. In order to find the best
approach, the parallel SPSO implementations were
tested on two electromagnetic problems the
TEAM22 benchmark problem and Loney’s solenoid
problem.
In the case of TEAM 22 benchmark problem the
fastest solution was the Pthreads implementation
running on a multiprocessor architecture, which
outperformed a CUDA implementation up to 17
times. For the Loney’s solenoid problem the fastest
approach was the CUDA implementation running on
a GPU which proved to be up to 10 times faster.
In terms of solution fitness the most efficient
implementation was the one based on Pthreads, but
the difference compared with CUDA is not
significant. A priori generation of the random
numbers on host, followed by a transfer to the GPU
device, could further improve the solution quality
for CUDA implementation. In most of the cases, the
best solutions were achieved for a small SPSO
swarm size.
As we have seen, there is not a single most
efficient parallelization approach and the results are
highly dependent of the problem to be solved, the
objective function and its implementation features.
While in the case of complex problems like TEAM
22, with a large number of instructions and very
high level of branching, the best approach is based
on Pthreads, for problems with a lower level of
branching and small number of instructions, like
Loney’s solenoid, the most efficient approach is
GPGPU.
ACKNOWLEDGEMENTS
This work has been supported by the Romanian
Government in the frame of the PN-II-PT-PCCA-
2011-3 program, grant no. 5/2012, managed by
CNDI– UEFISCDI, ANCS.
REFERENCES
Bastos-Filho, Oliveira Junior, Nascimento, A. D. Ramos,
2010. Impact of the Random Number Generator
Quality on Particle Swarm Optimization Algorithm
Running on Graphic Processor Units. Proceedings of
the 10th International Conference on Hybrid
Intelligent Systems, pp. 85-90.
Bratton, Kennedy, 2007. Defining a standard for particle
swarm optimization. Proceedings of the IEEE Swarm
Intelligence Symposium, 2007.
Castro-Liera, Castro-Liera, Antonio-Castro, 2011. Parallel
particle swarm optimization using GPGPU.
Proceedings of the 7th Conference on Computability
in Europe (CIE-2011).
Chen, Rebican, Yusa, Miya, 2006. Fast simulation of ECT
signal due to a conductive crack of arbitrary width.
IEEE Transactions on Magnetics, vol. 42, pp. 683-
686.
Ciuprina, Ioan, Munteanu, 2002. Use of intelligent-particle
swarm optimization in electromagnetics. IEEE
Transactions on Magnetics, vol. 38 (2), pp. 1037-
1040.
Clerc, 2012. Standard particle swarm optimization. Open
access archive HAL (http://clerc.maurice.free.fr/pso/
SPSO_descriptions.pdf).
Di Barba, Gottvald, Savini, 1995. Global optimization of
Loney’s solenoid: A benchmark problem. Int. J. Appl.
Electromagn. Mech., vol. 6, no. 4, pp. 273–276.
Di Barba, Savini, 1995. Global optimization of Loney’s
solenoid by means of a deterministic approach. Int. J.
Appl. Electromagn. Mech., vol. 6, no. 4, pp. 247–254.
Duca, Duca, Ciuprina, Yilmaz, Altinoz, 2014, PSO
Algorithms and GPGPU Technique for
Electromagnetic Problems, in the International
Workshops on Optimization and Inverse Problems in
Electromagnetism (OIPE), Delft, The Netherlands.
(under review process, to be published by an ISI
indexed journal).
Duca, Rebican, Janousek, Smetana, Strapacova, 2014.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
72
PSO Based Techniques for NDT-ECT Inverse
Problems. In Electromagnetic Nondestructive
Evaluation (XVII), vol. 39, pp. 323 - 330. Capova, K.,
Udpa, L., Janousek, L., and Rao, B.P.C. (Eds.), IOS
Press, Amsterdam.
Duca, Tomescu, 2006. A Distributed Hybrid Optimization
System for NDET Inverse Problems. In Proceedings
of the International Symposium of Nonlinear Theory
and its Applications (NOLTA), pp. 1059 - 1062.
Bologna, Italy.
Han, Wang, Fan, 2013. The Research of PID Controller
Tuning Based on Parallel Particle Swarm
Optimization. Applied Mechanics and Materials -
Artificial Intelligence and Computational Algorithms,
vol. 433-435, pp. 583-586.
Hung, Wang, 2012. Accelerating parallel particle swarm
optimization via GPU. Optimization Methods &
Software, vol. 27, no. 1, pp. 33–51.
Ioan, Ciuprina, Szigeti, 1999. Embedded stochastic-
deterministic optimization method with accuracy
control. IEEE Transactions on Magnetics, vol. 35 , pp.
1702-1705.
Kennedy, Eberhart, 1995. Particle swarm optimization.
Proceedings of IEEE International Conference on
Neural Networks, pp. 1942-1948.
Li, Udpa, Udpa, 2004. Three-dimensional defect
reconstruction from eddy-current NDE signals using a
genetic local search algorithm. In IEEE Transaction
on Magnetics (2), vol. 40, pp. 410 - 417.
MPI, 2015. http://en.wikipedia.org/wiki/
Message_Passing_Interface.
Mussi, Cagnoni, Daolio, 2009. GPU-Based Road Sign
Detection using Particle Swarm Optimization.
Proceedings of the Ninth International Conference on
Intelligent Systems Design and Applications (ISDA
'09), pp. 152-157.
Mussi, Cagnoni, 2009. Particle Swarm Optimization
within the CUDA Architecture. Proceedings of the
11th Annual Conference on Genetic and Evolutionary
Computation (GECCO'09).
Mussi, Daolio, Cagnoni, 2011. Evaluation of parallel
particle swarm optimization algorithms within the
CUDA architecture. Information Sciences, pp. 4642-
4657.
Nvidia CUDA C programming guide, 2015. http://
docs.nvidia.com/cuda/cuda-c-programming-guide.
OpenMP, 2015. http://www.openmp.org.
Pan, Tasgetiren, Liang, 2008. A discrete particle swarm
optimization algorithm for the no-wait flowshop
scheduling problem with makespan and total flowtime
criteria. Journal Computers & Operations Research,
vol. 35, pp. 2807–2839.
POSIX Threads standard, 2008. http://standards.
ieee.org/findstds/standard/1003.1-2008.html.
POSIX Threads tutorial, 2015.
http://en.wikipedia.org/wiki/POSIX_Threads.
Pthreads tutorial, https://computing.llnl.gov/tutorials/
pthreads.
Roberge, Tarbouchi, 2013. Comparison of parallel particle
swarm optimizers for graphical processing units and
multicore processors. International Journal of
Computational Intelligence and Applications, vol. 12.
Solomon, Thulasiraman, Thulasiram, 2011. Collaborative
Multi-Swarm PSO for Task Matching using Graphics
Processing Units. Proceedings of the 13th Annual
Conference on Genetic and Evolutionary Computation
(GECCO'11).
Sun, Fang, Palade, Wua, Xu, 2011. Quantum-behaved
particle swarm optimization with Gaussian distributed
local attractor point. Applied Mathematics and
Computation, vol. 218, pp. 3763-3775.
Takagi, Fukutomi, 2001. Benchmark activities of eddy
current testing for steam generator tubes. In
Electromagnetic Nondestructive Evaluation (IV), vol.
17, pp. 235 - 252. J. Pavo, R. Albanese, T. Takagi and
S. S. Udpa (Eds.), IOS Press, Amsterdam.
Tanji, Matsushita, Sekiya, 2011. Acceleration of PSO for
Designing Class E Amplifier. International
Symposium on Nonlinear Theory and its Applications
(NOLTA), pp. 491-494.
TEAM22 benchmark problem, 2015.
http://www.compumag.org/jsite/team.html.
Thomas, Pattery, Hassaina, 2013. Optimum capacity
allocation of distributed generation units using parallel
PSO using Message Passing Interface. International
Journal of Research in Engineering and Technology,
vol. 2, pp. 216-219.
Wang, Wang, Yan, Wang, 2008. An adaptive version of
parallel MPSO with OpenMP for Uncapacitated
Facility Location problem. Control and Decision
Conference (CCDC), pp. 2387 - 2391.
Zhao-Hua, Jing-Xing, Wen, 2014. Multi-core based
parallelized cooperative PSO with immunity for large
scale optimization problem. Conference on Cloud
Computing and Internet of Things, pp. 96-100.
Zhou, Tan, 2009. GPU-based Parallel Particle Swarm
Optimization. Proceedings of the IEEE Congress on
Evolutionary Computation (CEC'09), pp. 1493-1500.
GPGPU Vs Multiprocessor SPSO Implementations to Solve Electromagnetic Optimization Problems
73
