Multi-Robot Cooperative Tasks using Combined Nature-Inspired
Techniques
Nunzia Palmieri
1,2
, Floriano de Rango
1
, Xin She Yang
2
and Salvatore Marano
1
1
Dept. Computer Engineering Modeling, Electronics, and Systems Science University of Calabria, Rende (CS), Italy
2
School of Science and Technology, Middlesex University The Burroughs, London, U.K.
Keywords: Swarm Intelligence, Swarm Robotics, Firefly Algorithm, Bio-Inspired Algorithm.
Abstract: In this paper, two metaheuristics are presented for exploration and mine disarming tasks performed by a
swarm of robots. The objective is to explore autonomously an unknown area in order to discover the mines,
disseminated in the area, and disarm them in cooperative manner since a mine needs multiple robots to disarm.
The problem is bi-objective: distributing in different regions the robots in order to explore the area in a
minimum amount of time and recruiting the robots in the same location to disarm the mines. While
autonomous exploration has been investigated in the past, we specifically focus on the issue of how the swarm
can inform its members about the detected mines, and guide robots to the locations. We propose two bio-
inspired strategies to coordinate the swarm: the first is based on the Ant Colony Optimization (ATS-RR) and
the other is based on the Firefly Algorithm (FTS-RR). Our experiments were conducted by simulations
evaluating the performance in terms of exploring and disarming time and the number of accesses in the
operative grid area applying both strategies in comparison with the Particle Swarm Optimization (PSO). The
results show that FTS-RR strategy performs better especially when the complexity of the tasks increases.
1 INTRODUCTION
In the robotics field, an important aspect of multiple
agents systems is the coordination that allows the
system accomplishes efficiently general tasks, such as
exploration, coverage and surveillance. Autonomous
robots, equipped with proper sensors, are deployed in
the environment to find the object of interest, i.e., fire
spots in the jungle, mines in unknown area, missing
black box from a crashed airplane, or to measure a
concentration of hazardous materials. The use of a
swarm of robots is utilized in these applications for
the expected benefits of reducing risks to humans,
lower cost, and improved efficiency (Bellingham and
Godin 2007).
Swarm robotics is a new approach to the
coordination of a multi robots system, that typically
consist of a population of simple agents interaction
locally with each other and with the environment. The
benefit of cooperation can be significant in situation
where global knowledge of the environment does not
exist. Individuals within the group interact according
to the swarm intelligence algorithms by exchanging
information that is useful for performing the tasks
collectively.
In our collective construction task, there are some
mines randomly distributed in an unknown area. The
robots should first search for these mines
individually, but for disarming task, multiple robots
are needed to work together. The problem is not a
pure exploration: on one hand, it is required for robots
to cover as much area as possible in the minimum
amount of time, avoiding any overlapping area. On
the other hand, the problem needs to allocate more
robots in the same area to disarm a mine. The problem
is a bi-objective optimization problem where robots
have to make decisions whether to explore the area or
to help other robots to disarm the detected mines.
Because the problem of the unknown lands with
the constraint to disarm mine is a NP hard problem,
we proposed a combined approach using two bio-
inspired meta-heuristic approaches such as Ant
Colony Optimization (ACO) and Firefly algorithm
(FA) to perform the coordination task among robots.
Basically, each robot consists of two phases
during the task: searching and disarming. When there
is no detected mine, the robot status should be in the
searching phase, where robots are exploring the area
and searching for mines, taking into account the
quantity of pheromone perceived in the cells. Once
74
Palmieri, N., Rango, F., Yang, X. and Marano, S..
Multi-Robot Cooperative Tasks using Combined Nature-Inspired Techniques.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 74-82
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
mine is detected either by the robot itself or by its
neighbours, the robot status should be switched to the
disarming phase, under specific condition. The
strategy for the exploration task is designed according
to the main ideas of the ant system (Dorigo et al.,
2006). While the robots navigate, they deposit a
specific substance, the pheromone (the analogue of
the pheromone in biological ant systems), into the
environment. At each time/iteration, each robot
receives information from the pheromone and makes
a navigation decision: it chooses the area in which it
perceives a less quantity of pheromone because this
area has a greater probability to be unexplored (De
Rango and Palmieri, 2012; De Rango et al., 2015).
The algorithm for exploration has been previously
validated (De Rango and Palmieri, 2012) and this
paper presents the analysis of the recruiting strategies
in order to disarm the mines. The first is based on the
exploration strategy and uses the pheromone to attract
the robots in the area where the mine is placed. The
second strategy is based on the new recent bio-
inspired technique called Firefly Algorithm (FA)
where the robots that detect the mines become the
fireflies and try to attract the other robots according
with a certain formula (Yang, 2009; Yang, 2010).
These strategies were compared to the well known
Particle Swarm Optimization in order to evaluate the
better coordination mechanism for this problem. This
contribution can be effective because the recruiting
strategy can affect the exploration task and the overall
bi-objective exploring and recruiting tasks.
The paper is organized as follows. Section 2
introduces the related work. Section 3 describes the
firefly algorithm. In Section 4 we present the problem
statement. In Section 5 we present the distributed
cooperative algorithms for a multi-robot disarming
task. Section 6 presents the simulation results using a
java-based platform and Section 7 analyses the
quality of the solutions. To conclude the paper,
Section 8 outlines the main research conclusions and
discusses topics for future work.
2 RELATED WORK
Multi-robot exploration has received much attention
from the research community. Swarm robotic
searching algorithm is one of the most concerns of the
researchers besides those basic tasks. The swarm
intelligence shows great ability in scalable, flexibility
and robustness and is suitable for real life applications
with the aid of various existing strategies. Within the
context of swarm robotics, most work on cooperative
exploration is based on biologically behaviour and
indirect stigmergic communication (rather than on
local information, which can be applied to systems
related to GPS, maps, wireless communications).
This approach is typically inspired by the behaviour
of certain types of animals, like the ants, that use
chemical substances known as pheromone to induce
behavioural changes in other members of the same
species (Russell, 1999; Sugawara et al., 2004; Garnier
et al., 2007; Ducatelle et al., 2011, Masàr, 2013).
Other authors experiment with chemical
pheromone traces, e.g. using alcohol (Fujisawa et al.,
2008) or using a special phosphorescent glowing
paint (Mayet, 2010). Another approach is the
pheromone robotics where robots spread out over an
area and indicate the direction to a goal robot using
infrared communication (Payton et al., 2001). In our
approach, during the exploration the robots sign/mark
the crossed cell through the scent that can be detected
by the other robots; the robots choose the cell that has
the lowest quantity of substance to allow the
exploration of the unvisited cells in order to cover the
overall area in less time (De Rango and Palmieri,
2012).
The self-organizing properties of animal swarms
such as insects have been studied for better
understanding of the underlying concept of
decentralized decision-making in nature, but it also
gave a new approach in applications to multi-agent
systems engineering and robotics. Bio-inspired
approaches have been proposed for multi-robot
division of labour in applications such as exploration
and path formation, or cooperative transport and prey
retrieval. Within the context of swarm robotics, most
work on cooperative tasks is based on social
behaviour like Ant Colony Optimization (Dorigo et
al., 2006), Particle Swarm Optimization (Meng and
Gan, 2008) Bee Algorithm (Jevtic et al., 2012).
For sharing information and accomplishing the
tasks there are, basically, three ways of information
sharing in the swarm: direct communication
(wireless, GPS), communication through
environment (stigmergy) and sensing. More than one
type of interaction can be used in one swarm, for
instance, each robot senses the environment and
communicates with their neighbour. Balch (Balch,
2005) discussed the influences of three types of
communications on the swarm performance and Tan
(Tan and Zheng, 2013) presents an accurate analysis
of the different type of communication and the impact
in a behaviour of swarm.
In this paper, we considered the spatial and
temporal dispersion of the pheromone to make the
scenario more realistic (De Rango and Palmieri,
2012). While walking, the robots leave pheromone,
Multi-Robot Cooperative Tasks using Combined Nature-Inspired Techniques
75

which marks the cells they took. This chemical
substance can be detected by other robots. After a
while, the concentration of pheromone decreases due
to the evaporation and diffusion associated with the
distance and with the time; in this way we can allow
continuous coverage of an area via implicit
coordination. The other robots, through proper
sensors, smell the scent in the environment and move
in the direction with a minimum amount of
pheromone that corresponds to an area less occupied
and probably an unexplored area. On the other hand,
in order to deactivate the mines, the first robot that
detects a mine (recruiter) in a cell, sprays another
scent smelled by the robots; in this case the robots
move into the cells with a higher concentration of
pheromone and reach the area where to deactivate the
mines. In this attraction strategy of the recruiter,
another recent and novel bio-inspired approach
inspired by other insects such as fireflies has been
investigated in this work so as to see the effectiveness
of the algorithm and potential use of different insect
behaviour on the robot coordination task and their
performance. The algorithm inspired by fireflies is
called Firefly algorithm (FA) and is summarized in
the next section.
3 FIREFLY ALGORITHM
The firefly algorithm is a nature-inspired meta-
heuristic algorithm developed in 2008 by Xin-She
Yang to solve optimization problems (Yang, 2009;
Yang, 2010; Yang, 2014). The algorithm is based on
the social flashing behavior of fireflies in nature. The
key ingredients of the method are the variations of
light intensity and formulation of attractiveness. In
general, the attractiveness of an individual is assumed
to be proportional to their brightness, which in turn is
associated with the encoded objective function.
In the firefly algorithm, there are three idealized
rules, which are based on some of the major flashing
characteristics of real fireflies. They are:
1. All fireflies are unisex, so that one firefly will
be attracted to other fireflies regardless of their
sex;
2. The degree of attractiveness of a firefly is
proportional to its brightness, which decreases
as the distance from the other firefly increases
due to the fact that the airabsorbs light. For any
two flashing fireflies, the less bright one will
move towards the brighter one. If there is not
a brighter or more attractive firefly than a
particular one in the neighborhood, it will then
move randomly;
3. The brightness or light intensity of a firefly is
determined by the value of the objective
function of a given problem.
The distance between any two fireflies i and j, at
positions X
i
and X
j
, respectively, can be defined as the
Cartesian or Euclidean distance as follows:
∑
,
,
(1)
where x
i,k
is the k-th component of the spatial
coordinate X
i
of the i-th firefly and D is the number of
dimensions.
In the firefly algorithm, as the attractiveness function
of a firefly j, one should select any monotonically
decreasing function of the distance to the chosen
firefly, e.g., the exponential function:
(2)
where r
ij
is the distance defined as in Eq. (1), β
0
is the
initial attractiveness at r
0
, and γ is an absorption
coefficient at the source which controls the decrease
of the light intensity.
The movement of a firefly i which is attracted by a
more attractive (i.e., brighter) firefly j is governed by
the following evolution equation:
1
2
(3)
where the first term on the right-hand side is the
current position of the firefly, in our case a mine, the
second term is used for considering the attractiveness
of the firefly to light intensity seen by adjacent
fireflies, and the third term is used for the random
movement of a firefly in case there are not any
brighter ones. The coefficient α is a randomization
parameter determined by the problem of interest,
while σ is a random number generator uniformly
distributed in the space [0, 1].
Furthermore, we look at equation (3), thus non linear
equation provides much richer characteristics. Firstly,
if γ is very large, then attractiveness decreases too
quickly, this means that the second term in (3) became
negligible, leading to the standard simulated
annealing (SA). Secondly, if γ is very small ( i.e. →
0 ), then the exponential factor
→1 and FA
reduces to a variant of particle swarm optimization
(PSO). Also, the randomization term can be extended
to other distributions such as Lévy flight.
Furthermore, FA uses non linear updating equation,
which can produce rich behavior and higher
convergence than linear updating equation used for
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
76

example in standard PSO. Regarding the parameters
setting, parametric studies suggest that
0
=1 can be
used for most application; γ should related to the
scaling L. In general, we can set
(Yang, 2014).
4 PROBLEM STATEMENT
We consider an environment assuming that it is
discretized into equally spaced cells that contains a
certain number of mines. Each cell has the potential
to consider three states: free, occupied by mine,
occupied by robot. Robots can move among cells and
they can have just local information about robots
(neighbors) or regions to explore (neighbor cells) in
order to provide a scalable strategy.
The considered scenario is presented under this
assumption:
1) The robots are equipped with proper sensors
that are able to deposit and smell the chemical
substances (pheromones) leaved by the other
robots; for exploration task they make
probabilistic decision based on amount of
pheromone in the cells. The exploration
strategy is the same for the recruiting
strategies.
2) The robots are equipped with proper sensor to
detect the mines.
3) The robots can move on a cell-by-cell basis to
explore new cells or to go towards the mine.
The robots during the exploration spray a scent
(pheromone) into the cells to support the navigation
of the others. In the algorithm, the robots decide the
direction of the movement relying on a probabilistic
law inherited by swarm intelligence and swarm
robotics techniques. The scent evaporates not only
due to diffusion effects in the time, but also in the
space according to the distance; this allows a higher
concentration of scent in the cell where the robot is
moving and a lower concentration depending on the
distance.
Let M be the matrix of size mxn representing the
coverage area of size mxn. Let M(i,j) be the cell in the
matrix with row i and column j. Let z be the number
of mines on a set MS to distribute on the grid in a
random fashion (e.g., it is applied a uniform
distribution on X and Y axes). The MS set is
characterized by the coordinates of the mines. For
example,
12,7,10,5,4,3MS
indicates that there
are 3 mines in the area with the coordinates (3,4),
(5,10) and (7,12). The robots can be placed on the
same initial cell or can be randomly distributed on the
grid area. It is assumed that each robot in a cell M(i,j)
can move just in the neighbor cells through discrete
movements. Let t
e
be the time necessary for a robot to
consider a cell, and let t
d
be the time necessary to
disarm a mine once it has been detected. It is assumed
that a fixed number of robots (rd
min
) are necessary to
disarm a mine; this means that for the exploration task
robots can be distributed among the area because each
robot can independently explore the cells, whereas for
the mine detection, more robots need to be recruited
in order to perform the task. M (i, j )_a is a variable
representing the number of robots (accesses) that
passed through the cell (i,j).
For the problem we define an bi-objective
function as both the time to detect and the disarming
the mine through the exploration on the overall grid.
e
tmin
and
z
i
id
t
1
,
min
(4a)
subject to
1_, ajiM
njmi ...1;...1
/
Mji ,
min
_, rdajiM
with
MSji ,
This is a bi-objective optimization problem and its
solutions will result in a Pareto front. However, in
order to solve this problem more effectively, for
simplicity, we will combine these two objectives to
form a single objective optimization problem so as to
minimize the overall total time as follows:
z
i
idetot
ttT
1
,
minmin
(4b)
subject to
,_1∀1,..;1,…/
,
∈
,
,
∈
The law used by the robots to choose the cells during
the movement is presented below (De Rango and
Palmieri 2012).
We consider a robot in a cell s and it will attribute
to the set of next cells v
i
following a probability as:
sNvsvp
i
sNi
t
i
vt
i
v
t
i
vt
i
v
i
,
,,
,,
(5)
where (p(v
i
|s) represents the probability that the
robot, that is in the cell s, chooses the cell v
i
; N(s) is
the set of neighbors to the cells, τ
vi,t
is the amount of
pheromone in the cell v
i
; ɳ
vi,t
is the heuristic
Multi-Robot Cooperative Tasks using Combined Nature-Inspired Techniques
77

parameter introduced to make the model more
realistic. In addition,
and θ are two parameters
which affect respectively the pheromone and
heuristic values.
Taking into account the spatial dispersion of the scent
and the temporal dispersion in the amount of
pheromone in the cell v where the robot will move
during the exploration is:
,
,
(6)
In order to explore different areas of the environment,
the robots choose the cell with a minimum amount of
pheromone (MINIMUM_TRACE_FOLLOWER),
corresponding to cells that probably are less
frequented and therefore not explored cells. The
chosen cell will be selected according with eq. (5):
svpv
inext
|min
sNv
i
(7)
5 BIO-INSPIRED APPROACH
FOR THE DISARMING TASK
The purpose of the problem is to discover all mines
disseminated in the area and to disarm them. In the
first strategy the first robot that detects a mine
becomes a recruiter,which on the basis of the
recruiting startegy can spray a scent in order to
inform the other robots about the presence of a mine
and to recruit other robots for the disarming task
(indirect communication).
Alternatively, in the second startegy, the robots are
equipped by wireless module and the recruiters can
send a packet where putting the information about the
mine position (this can be useful for the FA based
strategy).
We assumed that the robots are not able to
communicate in a multi-hop manner but just via a
direct message (single-hop) (using for example a
wireless radio). Each robot can only communicate
with its neighbors. Two robots are defined as
neighbours if the distance between them is less than a
pre-specified communication range. In the following
section, the recruitment issue is formalised in order to
apply the proposed combination of the two bio-
inspired techniques.
5.1 Ant-based based Team Strategy for
Robots Recruitment (ATS-RR)
For this strategy we assume that the robots are
equipped by sensor that perceived a pheromone,
different by the pheromone used for the exploration.
The robots communicate with others through the
environment (indirect communication).
We considered that the mine disarming time is equal
to the total evaporation time of substance (scent); in
this way when the mine is disarmed, the robots
involved in this operation will not be affected by scent
trails.
We assume t is the time in which the robot r
detected a mine and it deposits the substance. The
robot r continues to spray until all necessary robots
reach its position.
If m is the time needed to disarm the mine, the law for
the evaporation of the scent is the following:
0
1
1
ttt
m
(8)
where ζ
t0
is the substance sprayed when the robot
detetects a mine. At the beginning ζ
t
= ζ
t0.
In this way after m steps ζ should be zeo so the scent
will not affect any more the movement of the other
robots. This assures that all robots will cover other
new space and disarm other mines completing the
task in an efficient and distributed manner.
5.2 Firefly based Team Strategy for
Robots Recruitment (FTS-RR)
For this task we considered the following assumption:
1) The robots are equipped by wireless module;
infact when a robot detects a mine, it becomes
a firefly and tries to attract other robots
sending messages via broadcast
communication to the robots in its wireless
range.
2) The robots, that receive messages by different
robots (fireflies), evaluate the light of fireflies
and choose the best firefly (at minimum
distance) and move toward firefly according to
a modified Discrete Firefly Algorithm.
When a robot finds a mine, during the exploration
task, it applies the FTS-RR and becomes the recruiter
of the other robots in order to disarm the mine. For
this purpose, in FTS-RR strategy, it becomes a firefly
and it tries to attract the other robots on the basis of
the mine position. The original version of FA is
applied in the continuous space, but in our case we
modified the algorithm in order to fit with our
problem. In our case, the robots can move in a
discrete space because they can go just in the
contiguous cells step-by-step. This means that when
a robot perceives at a distance the presence of a firefly
(the recruiter robot) and it is in a cell with coordinates
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
78
x
i
and y
i
, it can move according with the FA attraction
rules such as expressed below:
)
)
(9)
where x
j
and y
j
represent the coordinates of detected
mine translated in terms of row and column of the
matrix area. r
ij
is the Euclidean distance between
mine (or recruiter) and robot that moves towards the
mine. The robot movement is conditioned by mine
(recruiter) position in the second term of the formula
(9) and by a random component in the third term. This
last term is useful to avoid that more robots go
towards the same mine if more mines are distributed
on the land (this avoids the local minimum in order to
approach to a global optimum) Fig.1.
In order to modify the FA to a discrete version, the
robot movements have been considered through three
possible value updates for each coordinates:
1,0,1
such as expressed in Eq.(10). A robot r that
1
1
2
0
1
1
2
0
0
1
2
0
(10)
1
1
2
0
1
1
2
0
0
1
2
0
(11)
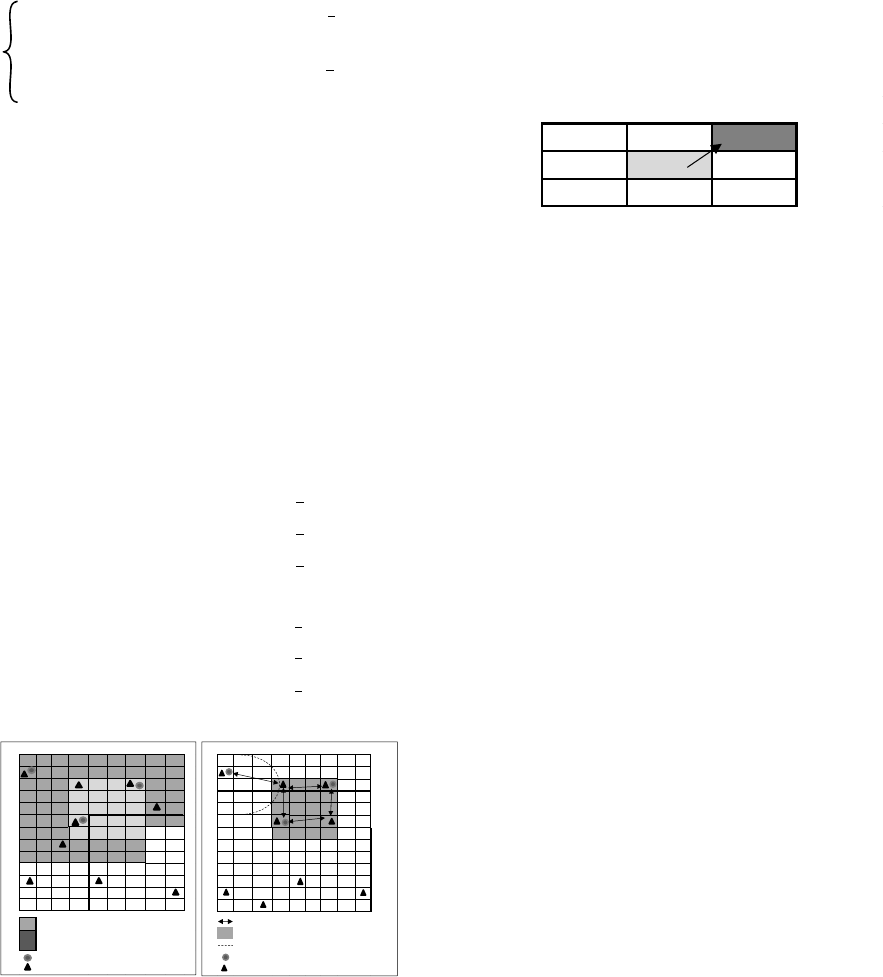
a) b)
Figure 1: Robots during the exploration receive two
recruiting calls because they are in an overlapped area. a)
In ATS-RR strategy the robots will choose the cell where
they perceive a greater quantity of pheromone; b) the FTS-
RR strategy tries to coordinate better the robots in the
disarming task considering the distance from the recruiter.
is in the cell of coordinates x
i
and y
i
such as depicted
in Fig.2 can move in eight possible cells according
with the three possible values attributed to x
i
and y
i
.
For example if applying eq.10 and eq.11 and the
result is {-1,+1} , the robot will move in the cell with
coordinates { x
i-1
; y
i+1
} such as depicted in Fig.2
Figure 2: Possible movements for a robot on the basis of the
x
i
and y
i
values.
6 PERFORMANCE
COMPARISON
In this section, we evaluate the performance of the
two proposed algorithms in comparison with the well
known Particle Swarm Optimization, focusing on the
time to cover all unknown area and disarm all mines
and the number of accesses in the cells in order to see
the effectiveness of the joint exploration task (space
distribution) and disarming task (space
concentration).The specific FTS-RR parameters were
set as follows:
=1;
=0.2; ϒ=1/L where L is max{m,
n} where m and n are the number of rows and columns
of the matrix M, respectively. For the ATS-RR, the
parameter values were set as follow: =1, θ=1; ɳ=0.9.
We considered different scenarios by varying the
minimum number of robots necessary to disarm a
mine, the total number of robots in the rescue area,
the dimension of grid and the number of mines. To
highlight the performance benefits, we use random
positions of the mines and the robots in the area by
varyng the number of robots so as to investigate the
performance of all strategies.
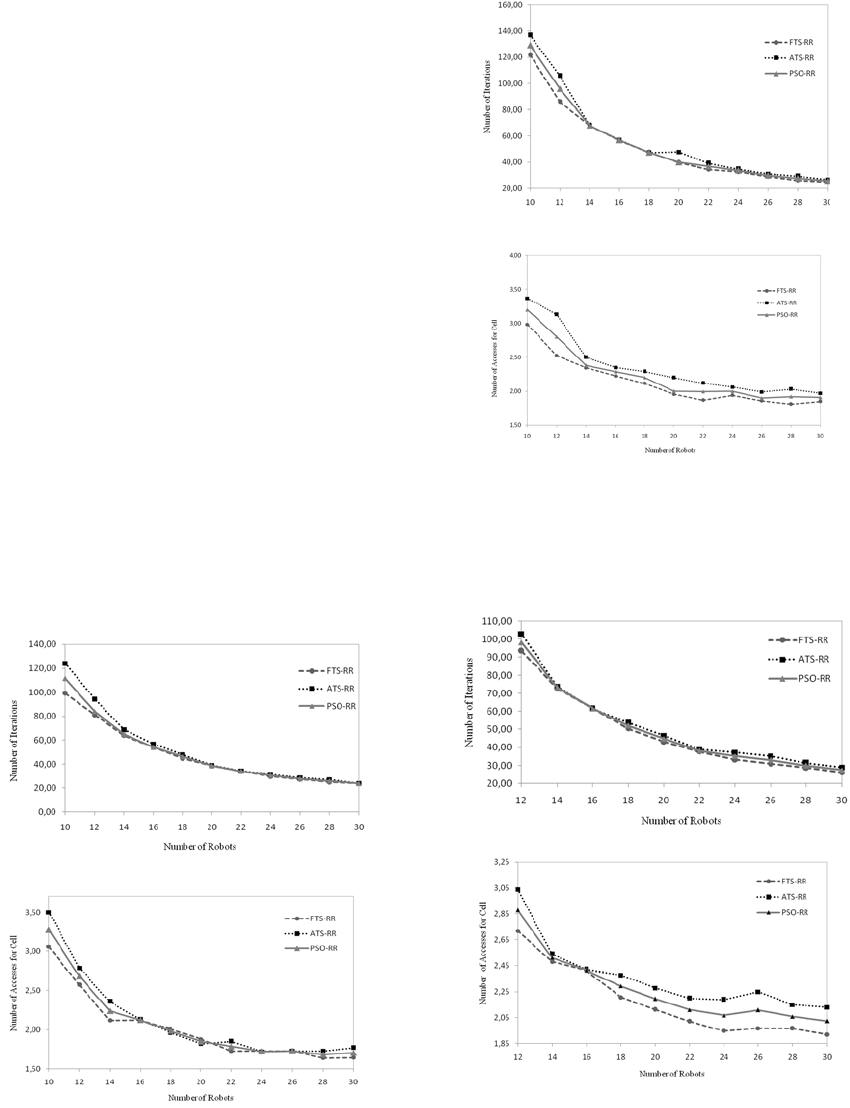
In Figures 3, 4 and 5 the number of mines and the grid
area have been fixed, respectively, to 3 and 20x20.
In Fig.3a and 3b, a comparison of the three algorithms
is depicted. In particular, it is shown the time to
complete both tasks measured as the number of
iterations and the number of accesses in the cells. The
convergence time and number of accesses in the cells
was averaged over 50 independent simulation runs in
order to enter in the 5% of confidence interval.
It is possible to see that the FTS-RR strategy performs
better mainly when the number of robots is low. This
is due to the better robot recruitment when a mine is
discovered that is able to balance the robot
coordination and movements among all mines. On the
Overlapped area
Mine
Robot
Area in which robots perceive the mine
pheromone
rij
Overlappedarea
Wirel e ssrange
Mine
Robot
y
i
x
i
‐1,y
i
‐1x
i
‐1,y
i
x
i
‐1,y
i
+1
x
i
x
i
,y
i
‐1r x
i
,y
i
+1
x
i
+1,y
i
‐1x
i
+1,y
i
x
i
+1,y
i
+1
Multi-Robot Cooperative Tasks using Combined Nature-Inspired Techniques
79
other hand, when the number of robots increases and
the number of minimum robots to disarm a mine is
equal to 2, ATS-RR, FTS-RR and PSO-RR are
similar because the high number of robots in
comparison to the number of mines allows to
complete both tasks in a lower time and no significant
difference between the strategies is so evident. The
number of accesses in the cells was plotted in Fig.3b.
Simulations show that FTS-RR is able to balance
better the robots in the recruitment phase considering
that the exploration phase is common to all
algorithms. This determines that a lower average
number of accesses in the cells can be obtained in
FTS-RR in comparison with ATS-RR and PSO-RR.
The same considerations can be made when the
number of robots needed to disarm a mine is 3(Fig.
4). An interesting result is shown in Fig 5. In these
cases, FTS-RR performs better for both low and high
numbers of robots in the convergence time especially
in comparison with the ATS-RR. This is due to the
most effective recruitment strategy that is able to
better distribute robots when, in the overlapping area,
more recruiters can engage robots for disarming. In
this case, the use of distance and the firefly algorithm
allows robots to spread over different mines avoiding
going towards the same mines to disarm. The overall
effect is a reduction in the task execution time.
a)
b)
Figure 3: Comparison between ATS-RR, FTS-RR and PSO
evaluating with 3 mines and 2 robots per mine to disarm
and increasing number of robots: a) number of iterations; b)
number of accesses in the cell.
a)
b)
Figure 4: Comparison between ATS-RR, FTS-RR and PSO
evaluating with 3 mines and 3 robots per mine to disarm
and increasing number of robots: a) number of iterations; b)
number of accesses in the cell.
a)
b)
Figure 5: Comparison between ATS-RR, FTS-RR and PSO
evaluating with 3 mines and 4 robots per mine to disarm
and increasing number of robots: a) number of iterations; b)
number of accesses in the cell.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
80
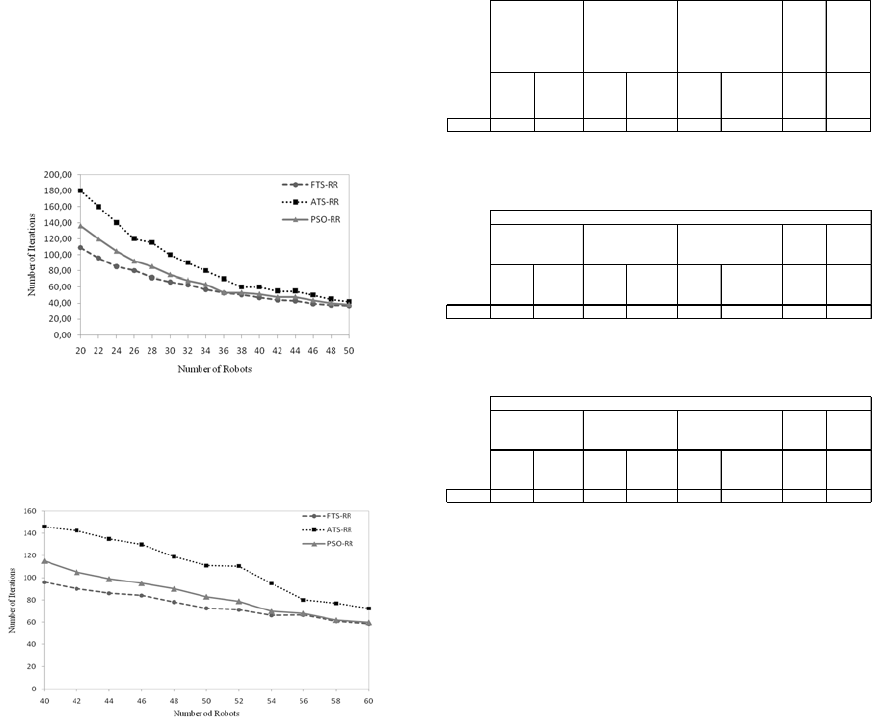
Concerning the number of accesses is much lower in
the FTS-RR. Increasing the complexity of the task the
difference between the three different algorithms, in
terms of overall time to complete the tasks, is greater
(Fig.6 and Fig. 7). This means that the best
performing of recruiting task can affect indirectly the
discovery task leading to a better distribution of
robots among mines to disarm and consequently to
explore the novel un-explored cells.
Figure 6: Comparison between ATS-RR, FTS-RR and
PSO, evaluating with 5 mines and 4 robots per mine to
disarm and increasing number of robots in a 30x30 gird
map.
Figure 7: Comparison between ATS-RR, FTS-RR and PSO
in terms of overall time, evaluating with 10 mines and 4
robots per mine to disarm and increasing number of robots
in a grid 40x40.
7 SOLUTION QUALITY
ANALYSIS
To validate the quality of solutions and results of the
three metaheuristics we have also considered the p
values of Student t-tests. The t-tests were used to
analyze the relationships between the results obtained
from the three metaheuristics. The parameter of
interest is the p-value.
Table I, Table II and Table III show the p-value
obtained from the t-tests using all above simulation
results by considering each parameter (the number of
interactions and the number of accesses in the cell)
for all considered scenario.
Table 1: Results of p values in the t Test for ATS-RR and
FTS-RR.
Table 2: Results of p values in the t Test for ATS-RR and
PSO-RR.
Table 3: Results of p values in the t Test for FTS-RR and
PSO-RR.
By analyzing the experimental results, it can be
observed a significant difference between the ATS-
RR and FTS-RR and ATS-RR and the PSO-RR. In all
considered scenario the p-value < 0.05, so there is a
strong statistic evidence of the difference between the
strategies. Regarding to the PSO-RR and the FTS-RR
analyzing the results (Table III) it can be observed
that the p-value <0.05 except for the Scenario 1 and
2. For other Scenario the p-value <0.05. This
confirms that the FTS-RR exhibits superior
performance when the complexity of tasks, in terms
of dimension of operative area, number of mines and
number of robots need to disarm a mine, increases.
8 CONCLUSION
Novel bio-inspired self-organizing coordination
algorithms are proposed for a distributed multi robot
coordination in a mined region.
For this purpose, two different strategies for the
mine disarming task combined with an Ant-based
space discovery strategy are proposed. The first
strategy ATS-RR isbased on Ant Colony
optimization, and the other one is based on the Firefly
Algorithm (FTS-RR). We compare both startegies
with the well known Particle Swarm Optimization.
By extensive simulations,we have concluded that the
FTS-RR can perform better in terms of the time to
Scenario
4
(Fig.6)
Scenario
5
(Fig.7)
Number
of
Iteration
Numberof
Accessin
thecells
Number
of
Iteration
Numberof
Accessin
thecells
Number
of
Iteration
Numberof
Accessinthe
cells
Number
of
Iteration
Number
of
Iteration
pvalue 0,0362 0,0261 0,0447 0,00342 0,02976 0,00172 0,001153 1,32E‐05
Scenario1
(Fig.3a,Fig.3b)
Scenario2
(Fig.4a,4b)
Scenario
3
(Fig.5a,5b)
Scenario
4
(Fig.6)
Scenario
5
(Fig.7)
Number
of
Iteration
Numberof
Accessin
thecells
Number
of
Iteration
Numberof
Accessin
thecells
Number
of
Iteration
Numberof
Accessinthe
cells
Number
of
Iteration
Number
of
Iteration
pvalue 0,0552 0,0328 0,0476 0,00048 0,0347 0,00368 0,003667 0,00030
Scenario1
(Fig.3a,Fig.3b)
Scenario2
(Fig.4a,4b)
Scenario3
(Fig.5a,5b)
ATS‐RRVSPSO‐RR
Scenario
4
(Fig.6)
Scenario
5
(Fig.7)
Number
of
Iteration
Numberof
Accessin
thecells
Number
of
Iteration
Numberof
Accessin
thecells
Number
of
Iteration
Numberof
Accessinthe
cells
Number
of
Iteration
Number
of
Iteration
pvalue 0,0623 0,0522 0,0524 0,001524 0,0495 0,0045 0,00667 0,00364
FTS‐RRVSPSO‐RR
Scenario1
(Fig.3a,Fig.3b)
Scenario2
(Fig.4a,4b)
Scenario3
(Fig.5a,5b)
Multi-Robot Cooperative Tasks using Combined Nature-Inspired Techniques
81
complete the task and the number of acccesses in the
cell, leading to a better distribution of robots with a
better combined time for both mine disarming and
exploration tasks expecially when the complexity of
the task increases.
Possible directions for future work can be followed.
Firstly, it would be very useful to vary the ACO and
FFA parameters and then evaluate their performance.
Secondly, it will also be fruitful to study the energy
consumed by the robots. Finally, mobile targets can
be a much better and realistic extension of the current
work. It can be expected that this present work can
form a basis for further extension and research.
REFERENCES
Balch, T. (2005). Communication, diversity and learning:
cornerstones of swarm behaviour. In: Swarm robotics,
lecture notes in computer science, vol.3342. Springer;
p. 21e30.
Bellingham, J. D. and Godin, M. (2007). Robotics in
Remote and Hostile Environments. Science, vol. 318,
pp. 1098-1102.
De Rango, F. and Palmieri, N. (2012). A swarm-based robot
team coordination protocol for mine detection and
unknown space discovery. In 8th Int. Conf. on Wireless
Communications and Mobile Computing (IWCMC), p.
703-709.
De Rango, F., Palmieri N.,Yang X-S, and Marano. (2015).
Bio-inspired Exploring and Recruiting Tasks in a Team
of Distributed Robots over Mined Regions. In
International Symposium on Performance Evaluation
of Computer and Telecommunication System
(SPECTS).
Dorigo, M., Birattari, M. and Stutzle, T. (2006). Ant colony
optimization. IEEE Comp. Intell. Mag., Vol. 1, No. 4,
28–39.
Ducatelle, F., Di Caro, G.A., Pinciroli, C. and Gambardella
L.M,. (2011). Selforganized cooperation between
robotic swarms. Swarm Intelligence, 5(2):73–96.
Fujisawa, R., Dobata, S., Kubota, d., Imamura, H., and
Matsuno, F. (2008). Dependency by concentration of
pheromone trail for multiple robots. In Proceedings of
ANTS 2008, 6th International Workshop on Ant
Algorithms and Swarm Intelligence, volume 4217 of
LNCS, pages 283–290. Springer.
Garnier, S., Tache, F., Combe, M., Grimal, A., and
Theraulaz, G. (2007). Alice in pheromone land: An
experimental setup for the study of ant-like robots. In
Proc. of the IEEE Swarm Intelligence Symp. (SIS),
pages 37–44, Washington, DC, USA.
Jevtic, A., Gutiérrez, A., Andina, D. and Jamshidi, M.
(2012). Distributed Bees Algortithm for Task
Allocation in Swarm of Robots. IEEE Systems Journal,
Vol 6 NO 2.
Masár, M. (2013). A biologically inspired swarm robot
coordination algorithm for exploration and
surveillance. In Proc. 17th IEEE Int. Conf. on
Intelligent Engineering Systems INES, Budapest, pp.
271-275, ISBN 978-1-4799-0830-1.
Mayet, R., Roberz, J., Schmickl, T., & Crailsheim, K.
(2010). Antbots: a feasible visual emulation of
pheromone trails for swarm robots. In Proceedings of
the 7th international conference on swarm intelligence
(ANTS) (pp. 84–94).
Meng, Y., Gan, J. A. (2008). A distributed swarm
intelligence based algorithm for a cooperative
multirobot construction task. Swarm Intelligence
Symposium, IEEE Transactions, pp. 1-6.
Payton, D., Daily, M., Estowski, R., Howard, M., & Lee, C.
(2001). Pheromone robotics. Autonomous Robots,
11(3), 319–324.
Russell, R. (1999). Ant trails - An example for robots to
follow. In Proc. of IEEE Int. Conf. on Robotics and
Automation (ICRA), pp. 2698–2703.
Sugawara, K., Kazama, T., and Watanabe, T.(2004).
Foraging behavior of interacting robots with virtual
pheromone. In Proc. of the IEEE/RSJ Int. Conf. on
Intelligent Robots and Systems (IROS), pp. 3074–3079.
Tan, Y. and Zheng, Z-Y. (2013). Research Advance in
Swarm Robotics. Defence Technology 9(1):18–39.
Yang, X.S. (2009). Firefly algorithms for multimodal
optimization. Lectures Notes in Computer Science,
5792(2009) 169-178.
Yang, X.S. (2010). Firefly algorithm, stochastic test
functions and designoptimisation. Int. Journal of Bio-
Inspired Computation, 2(2) 78-84
Yang, X.S. (2014). Cuckoo Search and Firefly Algorithm
Theory and Applications. Book on Studies in
Computational Intelligence, ISBN: 978-3-319-02140-
9.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
82
