Assessing Vertex Relevance based on Community Detection
Paul Parau, Camelia Lemnaru and Rodica Potolea
Department of Computer Science, Technical University of Cluj-Napoca, Cluj-Napoca, Romania
Keywords:
Vertex Relevance, Commitment, Importance, Relative Commitment, Community Disruption.
Abstract:
The community structure of a network conveys information about the network as a whole, but it can also
provide insightful information about the individual vertices. Identifying the most relevant vertices in a net-
work can prove to be useful, especially in large networks. In this paper, we explore different alternatives for
assessing the relevance of a vertex based on the community structure of the network. We distinguish between
two relevant vertex properties - commitment and importance - and propose a new measure for quantifying
commitment, Relative Commitment. We also propose a strategy for estimating the importance of a vertex,
based on observing the disruption caused by removing it from the network. Ultimately, we propose a vertex
classification strategy based on commitment and importance, and discuss the aspects covered by each of the
two properties in capturing the relevance of a vertex.
1 INTRODUCTION
Networks are essential instruments in understanding
many different types of data: social networks (rep-
resenting people and their relationships), biological,
technological or even information networks (New-
man, 2003; Fortunato, 2010). The study of such net-
works becomes harder as the size of the networks in-
creases, and extracting useful information from a net-
work having hundreds of thousands or millions of ver-
tices becomes a real challenge. To extract relevant in-
formation from such networks one must look at their
underlying structural properties. One such property is
their community structure: in networks which have
a community structure, vertices form groups called
communities. The specific meaning of a community
depends on the data the network is based on. For ex-
ample, in a social network, a community can be a
group of friends, or people who frequently commu-
nicate with each other. Finding the community struc-
ture of a network can help us gain useful insights into
the organization of the network. Applications of com-
munity detection include: making recommendations
to people based on the preferences of other people in
their community, studying the structure of the inter-
net, and analyzing networks of metabolic pathways
or protein interactions (Newman, 2003).
By analyzing the community structure of a net-
work, one can gain very useful macroscopic informa-
tion. But what about the microscopic level? What in-
formation does a community structure convey about
individual vertices? Are some vertices more impor-
tant than others and in what way? Our aim is to find
answers to such questions by looking at how vertices
are connected both inside their own community and
outside and how important the vertices and their con-
nections are.
We initially focus on commitment, a property
which quantifies how strongly a vertex belongs to
its community. We analyze two existing mea-
sures for commitment, embeddedness (Lancichinetti
et al., 2010) and significance (Rosvall and Bergstrom,
2010), and propose a new measure - Relative Com-
mitment. We show, based on the results of system-
atic experiments, that commitment does not capture
all information pertaining to the relevance of a vertex
and thus we identify another property: importance,
which reveals information about how important a ver-
tex is in its own community. We propose community
disruption as an importance measure which evaluates
the effects of removing that vertex on the community.
Based on commitment and importance, we propose a
categorization of vertices. Our solution can be used
in any type of network. For instance, one can identify
community leaders in a social network or the most
relevant researchers in a scientific collaboration net-
work.
The rest of the paper is organized as follows: sec-
tion 2 discusses existing research related to measuring
vertex and community structure properties, section 3
46
Parau, P., Lemnaru, C. and Potolea, R..
Assessing Vertex Relevance based on Community Detection.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 1: KDIR, pages 46-56
ISBN: 978-989-758-158-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

describes the datasets and methods used in our exper-
iments, section 4 discusses the results obtained with
existing measures of commitment and in section 5 we
propose a new measure for commitment, describe a
strategy for estimating both vertex and edge impor-
tance and show how vertices can be categorized based
on commitment and importance.
2 RELATED WORK
In this section, after a brief description of commu-
nity detection, we describe existing vertex-level mea-
sures. Additionally, we discuss methods of quantify-
ing higher-level community structure properties, ele-
ments of which we will use throughout this paper.
2.1 Community Detection
A community is commonly defined as an area of the
network where the density of edges inside the com-
munity is greater than the density of the entire net-
work (Newman, 2003; Fortunato, 2010). The ver-
tices in a community usually share some common
traits and/or roles in the network. The collection of
communities in a graph is called community struc-
ture and community detection is the process of find-
ing the community structure of a network. Commu-
nities can share vertices (overlapping communities)
and community structures can be hierarchical, with
higher-level communities being composed of lower-
level communities.
There are many approaches for finding the com-
munity structure of a network. An important cate-
gory of algorithms are hierarchical algorithms, which
build a dendrogram based on a vertex similarity mea-
sure, where each level represents a possible com-
munity structure. The dendrogram can be built in
a top-down (divisive) or bottom-up (agglomerative)
approach (Fortunato and Castellano, 2008). Another
important category, first proposed by Newman (New-
man, 2004), are algorithms based on modularity op-
timization, a measure of the quality of the commu-
nity structure in a network. Infomap is a different
type of algorithm proposed by Rosvall and Bergstrom
(Rosvall and Bergstrom, 2008) which works by com-
pressing a description of the probability flow of ran-
dom walks in a network. The algorithm searches
for a community structure which minimizes the de-
scription length of a random walk. Studies evaluating
the performance of community detection algorithms
found the Infomap algorithm to be generally better
performing than alternatives (Lancichinetti and For-
tunato, 2009; Orman et al., 2012).
2.2 Vertex Measures
One of the simplest strategies to quantify the com-
mitment of a vertex to its community is embedded-
ness (Lancichinetti et al., 2010; Orman et al., 2012;
Palla et al., 2007). Embeddedness is a measure that
indicates how many neighbors of a vertex are in the
same community as the vertex and is defined (1) as
the ratio between the internal degree k
in
(number of
edges inside the community) and the total degree k
of the vertex. For a weighted graph, the formula is
a weighted one, considering the weights of the corre-
sponding edges instead of just counting them.
e =
k
in
k
(1)
As is shown in (Palla et al., 2007), vertices with
low embeddedness have a high likelihood of leaving
the community in the future. In real-world networks,
the majority of the vertices have an embeddedness
e = 1 (Lancichinetti et al., 2010; Orman et al., 2012),
since most of them are located inside their own com-
munities and do not have edges outside. The vertices
that have an embeddedness e < 1 are vertices located
at the fringes of their respective communities.
Also based on degree, Guimera and Amaral
(Guimera and Amaral, 2005) analyze the connectivity
of vertices and propose a number of universal roles for
them. They define the z-score of a vertex (2), where
κ
i
is the internal degree of vertex i,
¯
κ
s
i
is the average
internal degree of all the vertices in community s
i
and
σ
κ
s
i
is the standard deviation.
z
i
=
κ
i
−
¯
κ
s
i
σ
κ
s
i
(2)
Since this measure does not take connections to
vertices in other communities into account, two ver-
tices in the same community, with the same inter-
nal degree but different external degree will have the
same z-score. To distinguish between such vertices,
the authors define the participation coefficient of a
vertex i as shown in (3), where κ
is
is the degree with
community s, and k
i
is the total degree of the vertex.
A vertex with edges exclusively in its own community
has a participation coefficient of 0.
P
i
= 1 −
N
M
∑
s=1
κ
is
k
i
2
(3)
Jointly evaluating these measures, the authors de-
fined 7 roles for vertices: based on the value of the
z-score, vertices are community hubs if z
i
≥ 2.5 and
non-hubs if z
i
< 2.5. Based on the participation co-
efficient, which indicates how the connections of the
vertex are spread out among the communities of the
Assessing Vertex Relevance based on Community Detection
47

graph, vertices were further classified. In increasing
order of participation coefficient, non-hubs were clas-
sified as ultra-peripheral (R1), peripheral (R2), non-
hub connectors (R3) and non-hub kinless (R4) and
hubs were classified as provincial (R5), connector
(R6) or kinless hubs (R7). In section 5.3, we analyze
the way these universal roles compare to the vertex
categories we propose.
A way to find out which vertices are the most sig-
nificant is proposed by Rosvall and Bergstrom (Ros-
vall and Bergstrom, 2010). Their approach, called
significance clustering, uses a bootstrap resampling
technique to assess which vertices are significant in a
community. The basic idea is to generate a number of
networks derived from the original but with small per-
turbations to their connections and then apply a com-
munity detection algorithm on them. In each com-
munity, the largest subset of vertices that are clus-
tered together in at least 95% of the bootstrap net-
works is found by using simulated annealing. This
subset is called a significant subset. Communities are
significantly distinct from other communities if their
significant subset is not clustered together with any
other significant subset in at least 95% of the boot-
strap networks. Since significant vertices are unlikely
to leave the community when the network is slightly
perturbed, their significance can be considered a mea-
sure of commitment. It is important to note that this
method is independent of the community detection
method used and as such can be used with any algo-
rithm. This approach of generating slightly perturbed
graphs and analyzing differences in community struc-
ture was used in earlier research to determine the sta-
tistical significance of the identified community struc-
ture and will be described in more detail in the follow-
ing section.
2.3 Community Structure Significance
In (Karrer et al., 2008), the authors present a method
of measuring the significance of a community struc-
ture by determining its robustness to small perturba-
tions. The idea behind this is that a significant com-
munity structure will be robust to small perturbations,
whereas a community structure that is not statistically
significant will be sensitive to small changes. The
perturbation method they propose modifies the po-
sition of the edges of the network, maintaining the
same number of vertices and edges. Each edge of the
network will be deleted with a probability α. Each
deleted edge will be replaced with a new edge be-
tween two vertices chosen randomly with a proba-
bility given by the expected number of edges. The
expected number of edges between two vertices is de-
fined in equation (4), where k
i
and k
j
are the degrees
of the vertices i and j in the original network and m is
the total number of edges.
e
i j
=
k
i
k
j
2m
(4)
Not only does this perturbation method generate
networks with the same number of vertices and edges,
but the expected degree of vertices also remains the
same.
A number of perturbed networks is generated and
the difference between the original community struc-
ture and the community structure of the perturbed net-
works is measured. This is done by calculating an
information theoretic measure called Variation of In-
formation, defined in (5).
V I = −
∑
xy
P(x,y)log
P(x,y)
P(y)
−
∑
xy
P(x,y) log
P(x,y)
P(x)
(5)
Variation of Information measures how different
two community structures are based on the number
of vertices that are clustered together in both struc-
tures. P(x, y) is defined as the number of vertices that
appear in both communities divided by the total num-
ber of vertices, and P(x) and P(y) are defined as the
number of vertices that appear in community X and Y
respectively, divided by the total number of vertices.
This measure can be normalized by 1/log n, where
n is the total number of vertices in the graph. High
Variation of Information between the perturbed com-
munity structures and the original means that the orig-
inal community structure is not statistically signifi-
cant. Similar to significance clustering, this method
is independent of the community detection algorithm
used.
Related to the concept of measuring community
structure robustness by perturbing the graph is the re-
search presented in (Albert et al., 2000), which out-
lines a method of assessing the resilience of a network
by measuring its ability to carry information after re-
moving its vertices. The authors found that scale-free
networks are very resilient to random vertex removal
but highly vulnerable to targeted removal of the most
connected vertices.
3 EXPERIMENTAL DATA AND
METHODS
Given that the Infomap algorithm has been found to
be generally better performing than alternatives, we
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
48

Figure 1: The community structure of the Karate network
as identified by the Infomap algorithm.
Figure 2: The largest communities in the Netscience net-
work in the top-level community structure, as identified by
the Infomap algorithm.
have chosen to use this algorithm
1
in our experiments.
We use two networks in our experiments:
Zachary’s Karate Club (Zachary, 1977) (henceforth
referred to as the Karate network) and a network of
coauthorships in network science compiled by New-
man in (Newman, 2006) (henceforth referred to as
the Netscience network). The Karate network repre-
sented in Figure 1 is one of the first and most studied
in network science and is an undirected, unweighted
graph that represents the relationships between mem-
bers of a karate club. It contains 78 edges and 34
vertices which are divided into three communities, as
identified by the Infomap algorithm. The Netscience
network represented in Figure 2 is an undirected,
weighted graph of scientists working in the field of
network theory. It contains 1589 vertices and 2742
edges. The Infomap algorithm found that this network
has a three-level hierarchical community structure.
The results of our experiments indicate that there
are actually two properties of vertices that are relevant
for their relationship with the community: commit-
ment, which quantifies how strongly a vertex belongs
to its community and importance, which should con-
vey information related to the relevance of the vertex
1
D. Edler and M. Rosvall, The MapEquation software
package, available online at http://www.mapequation.org.
to the structure of its community. Using the Karate
and Netscience networks, we have analyzed measures
that assess both commitment and importance and de-
termined categories of vertices based on these proper-
ties.
4 ANALYSIS OF EXISTING
MEASURES
This section presents an experimental assessment of
existing commitment measures: embeddedness and
significance. The evaluations were performed accord-
ing to the methodology described in the previous sec-
tion. We analyze the behavior of the two metrics, out-
lining their strengths and weaknesses.
4.1 Embeddedness
First we evaluated the embeddedness measure. Fig-
ure 3 shows histograms of embeddedness on the two
graphs. As we can observe from both histograms, val-
ues are strongly skewed towards 1, which suggests
that the majority of the vertices have connections only
inside their own communities. In fact, in the top-level
community structure in the Netscience network, ap-
proximately 98% of vertices have an embeddedness
equal to 1. As expected, the percent gets lower with
further decompositions of the community structure,
with 87% and 84% for levels 1 and 2 respectively, but
the distribution is still heavily skewed towards very
high values.
This highlights an important issue the embedded-
ness measure has: as was also observed in (Lanci-
chinetti et al., 2010; Orman et al., 2012), it appears
that in most real-world networks the majority of ver-
tices have connections only inside their own commu-
nities so the information conveyed by this measure
carries, in general, little meaning. Furthermore, if we
take for example the Karate network, the only connec-
tion of vertex 12 is inside its own community, so it has
an embeddedness of 1. Vertex 2 has 8 connections in-
side the community (to 75% of all vertices in the com-
munity) and one connection outside, so it has an em-
beddedness of 0.89. Intuitively however, one would
think that vertex 2 has a stronger commitment to the
community than vertex 12. The issue here is that em-
beddedness does not take the number (or indeed sum
of weights in a weighted network) of the connections
of a vertex into account, only the ratio between inter-
nal and external edges, which, while useful, does not
paint the whole picture.
Another issue with embeddedness can be ob-
served by looking at vertex 78 in level 2 of the
Assessing Vertex Relevance based on Community Detection
49

0
5 · 10
−2
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
0
5
10
15
Number of Vertices
0
5 · 10
−2
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
0
500
1,000
Embeddedness
Number of Vertices
Figure 3: Embeddedness histograms for the Karate network
(top) and level 2 of the Netscience network (bottom).
Netscience network. This vertex has an internal
weight of 16.25 and an external weight of 6.75 across
7 other communities. The embeddedness of this ver-
tex is 0.71, however the interior weight is far larger
than the weight towards any single other community.
Comparing the internal weight to the cumulative ex-
ternal weight creates a disadvantage for vertices who
are weakly connected to many other communities but
have a strong connection to their own community.
4.2 Significance
Next, we have analyzed the vertices based on their
significance. Instead of determining the significance
clusters as done in (Rosvall and Bergstrom, 2010),
we have used the perturbation method described in
(Karrer et al., 2008) to determine a significance mea-
sure for all vertices in the community structure of the
graph. The method we used is the following:
1. Generate a number (between 100 and 1000, more
on that later) of perturbed graphs with α = 0.2
(in every perturbed graph 20% of the edges were
moved).
2. Determine the community structure of each of
these perturbed graphs.
3. For each vertex, determine the percentage of per-
turbed graphs in which the vertex remained in the
same community as in the community structure of
the original graph.
The percentage computed in step 3 represents the
significance of the vertex, based on the idea that ver-
tices which remain in the same community after the
graph is slightly perturbed have a high commitment
to that community.
The first question that arises is how to determine
the corresponding communities of the same vertex in
two different community structures. This is necessary
in order to determine whether the vertex remained in
the same community or not after the graph was per-
turbed. To achieve this, we used the relative overlap
measure (Fortunato, 2010; Palla et al., 2007). Rel-
ative overlap (6) represents the number of vertices
shared between two communities, so in order to de-
termine the corresponding perturbed community we
choose the one with the highest relative overlap with
the original community.
s
i j
=
|X
i
T
Y
j
|
|X
i
S
Y
j
|
(6)
The next question we considered in the evalua-
tion process was how many perturbed graphs to gen-
erate? The authors of (Karrer et al., 2008) used a
number between 10 and 100, depending on the num-
ber of vertices of the network, while the authors in
(Rosvall and Bergstrom, 2010) used 1000 perturbed
graphs. The process of determining the significance
of a vertex is non-deterministic, since the perturba-
tions applied to the graph have a random element (see
section 2.3). Since the significance of a vertex is aver-
aged across all perturbed graphs, a higher number of
such graphs means a higher accuracy and reliability
in determining the measure, but also a higher com-
putation time because community detection has to be
performed for each of the perturbed graphs. Depend-
ing on the community detection algorithm used, this
can be rather computationally expensive. To deter-
mine what a good balance between accuracy and the
number of perturbed graphs would be, we calculated
the significance of the vertices in both networks for
100, 250, 500, 750 and 1000 perturbed graphs. We
repeated each experiment 3 times and computed the
average standard deviation of the significance values
(Figure 4).
As can be noticed, the gains in accuracy be-
come smaller the more perturbed graphs are gener-
ated. Based on this observation we can conclude
that on these networks, 750 or even 500 perturbed
graphs provide a good trade-off between computation
time and accuracy. Another interesting observation
is that the standard deviation follows the same pat-
tern for both networks, although they have very dif-
ferent sizes. Even more, the standard deviation for
the larger network is consistently smaller than for the
smaller network. This suggests that for large net-
works a smaller number of perturbed graphs is suf-
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
50
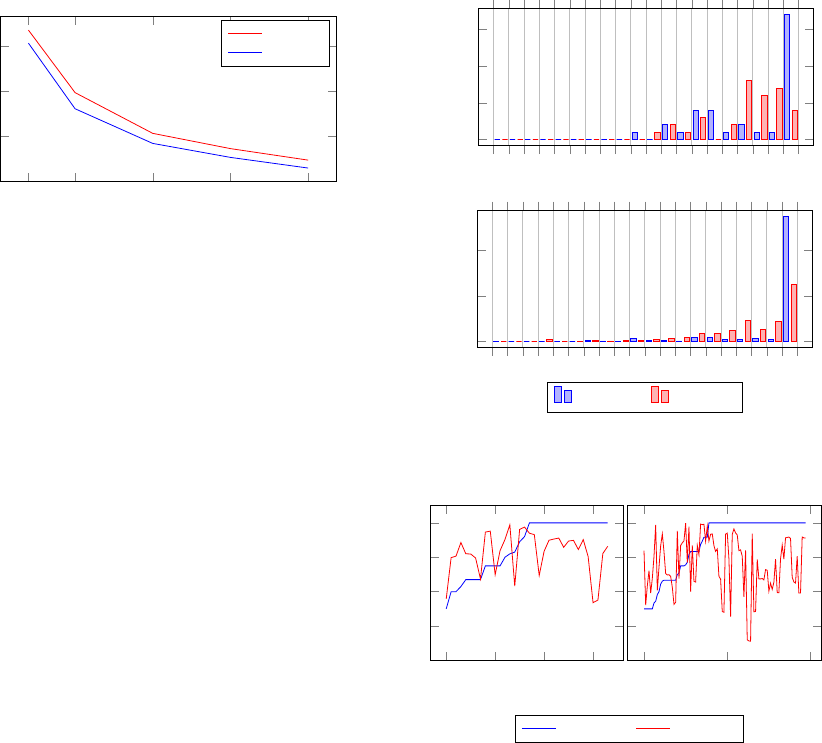
100
250 500 750
1,000
0.5
1
1.5
2
·10
−2
Number of perturbed graphs
Standard deviation
Karate
Netscience
Figure 4: Average standard deviation of significance.
ficient.
The significance results presented next are for
1000 perturbed graphs. Figure 5 shows histograms
comparing significance to embeddedness for both net-
works. We can observe that the distribution of signifi-
cance is much more uniform, which suggests that this
measure does not suffer from the issue shown in sec-
tion 4.1. By comparing the two measures (Figure 6)
we cannot observe a significant correlation between
them: vertices with high significance do not neces-
sarily have high embeddedness or vice-versa. In-
deed, Pearson’s correlation coefficient is r = 0.2 for
the Karate network and r = 0.01 for the Netscience
network. Since significance essentially measures the
resilience of the membership of a vertex to pertur-
bations and considering these results and the issues
with embeddedness we have highlighted in section
4.1, significance seems to be the better measure of the
two. We will be looking in more detail at the differ-
ences between embeddedness and significance in the
following section.
5 NEW VERTEX MEASURES
In this section, we first analyze the differences be-
tween significance and embeddedness and identify
factors that influence significance. Based on these
factors, we propose a new measure for commitment
called Relative Commitment. In section 5.2 we pro-
pose a method for assessing vertex importance by ob-
serving the effects of removing the vertex from the
graph and in section 5.3 we show how vertices can
be categorized based on measures of commitment and
importance.
5.1 Relative Commitment
As we determined earlier, significance appears to be
the better measure for assessing commitment. How-
ever, it carries a drawback: a large processing time.
Depending on the desired accuracy, the graph has to
0
5 · 10
−2
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
0
5
10
15
Number of Vertices
0
5 · 10
−2
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
0
500
1,000
Number of Vertices
Embeddedness Significance
Figure 5: Embeddedness and significance histograms of the
Karate network (top) and the level 2 community structure
of the Netscience network (bottom).
0 10 20 30
0.2
0.4
0.6
0.8
1
Vertex Id
0
50
100
Vertex Id
Embeddedness Significance
Figure 6: Embeddedness compared to significance in the
Karate network (left) and the biggest community in the
Netscience network (right). Vertices are sorted in increasing
order of embeddedness.
be perturbed and community detection has to be per-
formed many times, while embeddedness is a simple
calculation which has to be performed once for each
vertex. It would be advantageous to have a measure
computed as fast as embeddedness, but which can
capture the information conveyed by significance. To
this end, we investigated which other factors besides
the ratio between internal and external degree are im-
portant for the significance, by looking at the differ-
ences between the significance and the embeddedness
of vertices in the Karate network. We attempt to de-
fine an improved measure based on our findings.
The first issue we identified with embeddedness is
that it does not take the internal degree of the ver-
tex into account, only its ratio to the total degree,
which can be misleading. So, as a first improve-
ment to embeddedness we considered using the rela-
Assessing Vertex Relevance based on Community Detection
51

tive internal degree rk
in
i
of the vertex: k
in
i
/Max
s
(k
in
),
where k
in
i
represents the internal degree of vertex
i and Max
s
(k
in
) is the maximum internal degree in
community s. However, we observed that vertices
with a medium number of internal connections had
a score that was too low and thus we applied the loga-
rithmic formula in equation (7). In a weighted graph,
we can use the relative internal weight rw
in
i
, where
we replace the internal degree with internal weight in
equation (7).
rk
in
i
=
log(k
in
i
+ 1)
log(Max
s
(k
in
) + 1)
(7)
We also observed that there are vertices with a
relatively small number of connections, but with a
high significance. Looking at those vertices we re-
alized that they were connected to other vertices in
the same community that had a high internal degree,
so they were less likely to leave the community when
the graph was perturbed. A good example is vertex
15 in the Karate network which has only two connec-
tions in its community, so judging solely by relative
internal degree (considering that the maximum inter-
nal degree in that community is 14) one would think it
has a weak connection to the community. The signifi-
cance of vertex 15 is however high at 0.9, most likely
because it is connected to the two most connected ver-
tices in the community: 33 and 34. Considering this,
it seems natural that not only the internal degree, but
also the internal neighborhood (neighbors within the
community) of the vertex is an important factor for its
connection strength. It is important to note that the
internal neighborhood should only have a positive ef-
fect on the score of the vertex: a well-connected ver-
tex should not have its score lowered simply because
it is connected to low-degree vertices.
Similar to the previous point, we found that we
also have to look at the external neighborhood of a
vertex: a vertex that is well connected inside its own
community but has connections with well-connected
vertices in other communities will have a higher like-
lihood of leaving the community. A good example for
such a vertex is 32: it has an internal degree of 5, an
external degree of only 1 and is connected to vertices
33 and 34, so one would expect a high significance.
The significance is actually quite low, at 0.63, because
it is connected to vertex 1, which is the most con-
nected vertex in another community. One can view
highly connected vertices as attractors that exercise a
pulling force on their weaker-connected neighbors, so
neighbors both inside and outside of the community
have to be considered.
To summarize, we have identified the following
factors which should be considered for estimating
how strongly a vertex belongs to its own community
(i.e. measuring commitment):
• The internal degree
• The internal degree of its internal neighbors
• The internal degree of its external neighbors
Considering the fact that embeddedness does not
represent a sufficiently expressive metric for estimat-
ing the commitment of a vertex, and that significance
is computationally intensive, we propose a new mea-
sure for quantifying vertex commitment, which we
call Relative Commitment. We define the internal
score of a vertex to be the sum of the relative inter-
nal degrees of its internal neighbors and the external
score, the sum of the relative internal degrees of its
external neighbors. Relative Commitment is the ratio
between the internal score and the total score (internal
+ external), multiplied by the relative internal degree
of the vertex in question. Thus, we obtain the formula
in equation (8), where rk
in
represents the relative in-
ternal degree of the vertex and i and j denote the inter-
nal and external neighbors of the vertex, respectively.
rc = rk
in
∗
∑
i
rk
in
i
∑
i
rk
in
i
+
∑
j
rk
in
j
(8)
For a weighted graph, we use relative internal
weight instead of degree and additionally we use the
connection weight to each neighbor in the internal
and external score (9), where w
i
and w
j
represent the
weight of the connection with internal neighbor i and
external neighbor j, respectively.
rcw = rw
in
∗
∑
i
w
i
∗ rw
in
i
∑
i
w
i
∗ rw
in
i
+
∑
j
w
j
∗ rw
in
j
(9)
Figure 7 shows histograms comparing the Relative
Commitment to embeddedness and significance for
both Karate and Netscience networks. In the Karate
network the Relative Commitment values are on aver-
age lower than significance, while in the Netscience
network, we have more values of Relative Commit-
ment between 0.95 and 1.0.
Figure 8 shows Relative Commitment compared
to significance for both networks. As we can see,
there is a clear correlation between the two measures
for many vertices. For both networks, the correlation
coefficient r is approximately 0.59. This means that
the factors identified previously are indeed important
for the significance of the vertices. However, we can
see that there are still differences, vertices that have
a high Relative Commitment but a low significance or
vice-versa, so there are still aspects of significance we
have not covered in Relative Commitment. Still, even
in its current form, Relative Commitment represents a
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
52
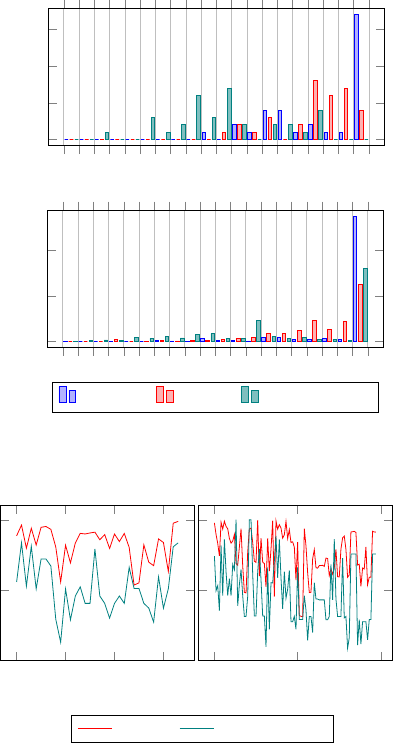
0
5 · 10
−2
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
0
5
10
15
Number of Vertices
0
5 · 10
−2
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
0
500
1,000
Number of Vertices
Embeddedness Significance Relative Commitment
Figure 7: Embeddedness, significance and Relative Com-
mitment histograms for the Karate network (top) and level
2 of the Netscience network (bottom).
0 10 20 30
0
0.5
1
Vertex Id
0
50
100
Vertex Id
Significance Relative Commitment
Figure 8: Significance compared to Relative Commitment
in the Karate network (left) and the biggest community in
the Netscience network (right).
good approximation of significance and can be used
in cases where the processing time of significance is
an impediment.
5.2 Vertex Importance
In addition to analyzing the commitment of vertices,
we wanted to assess the importance of a vertex by
looking at what happens to the community structure
if that vertex is removed from the graph. Based on
the idea that the more important a vertex is, the larger
the disruption caused will be, idea supported by the
findings in (Albert et al., 2000), we propose the fol-
lowing method of assessing vertex importance:
1. Remove vertex from graph
2. Determine community structure in this graph
3. Compute the difference between the original com-
munity structure and the new community structure
Steps 1 and 2 are straightforward. Step 3 involves
measuring the disruption the removal of the vertex
causes. In order to do this, we compute the normal-
ized version of the Variation of Information measure
defined in equation (5). When computing Variation of
Information, we remove the vertex from the original
community structure and then compare it to the new
community structure. There are two different types
of disruption of interest: the disruption caused to the
community of the vertex (community disruption) and
the disruption caused to the community structure as
a whole (community structure disruption). From the
standpoint of determining the importance of the ver-
tex for its own community, community disruption is
relevant. But, as we will see, community structure
disruption can also convey useful information.
The same method described above can be easily
applied on edges, to determine the most important
edges in a community. We will analyze vertices of the
Karate network using both vertex and edge omission.
5.2.1 Vertex Omission
Figure 9 shows the result of applying the described
vertex omission method on the Karate network. As
expected, community disruption ≤ community struc-
ture disruption. We can observe that disruption seems
to have a weak negative correlation with embedded-
ness: vertices with low embeddedness tend to have
non-zero disruption values. Community disruption
has a correlation coefficient r = −0.14 while for com-
munity structure disruption r = −0.29. At first im-
pression, it might seem that vertices that have em-
beddedness < 1 should cause community structure
disruption since they have both internal and external
edges. However, the negative correlation also appears
to hold for community disruption, where the disap-
pearance of external edges should have no negative
impact on the community. It is possible that vertices
with connections both inside and outside the commu-
nity tend to be the most influential.
We note that disruption does not seem to be cor-
related with significance (r = 0.09 and r = 0.16 for
community and community structure disruption, re-
spectively). There are vertices with high significance
and no disruption, and there are vertices with low sig-
nificance but whose removal disrupts the community.
At first glance, this represents a surprising result: one
would expect the removal of the most significant ver-
tices to be the most disruptive. However, after looking
at the vertices in these networks we can conclude the
following: measures like embeddedness, significance
Assessing Vertex Relevance based on Community Detection
53

0 10 20 30
0
0.5
1
Vertex Id
Embeddedness Significance
Comm. Disruption Comm. Structure Disruption
Figure 9: Disruption compared to embeddedness and sig-
nificance for the Karate network. Vertices are sorted in in-
creasing order of embeddedness.
and Relative Commitment measure the commitment
of a vertex to a community, the strength of the mem-
bership of that vertex. Disruption on the other hand
measures how important the vertex is for the structure
of the community. To elaborate on this, let us analyze
vertices in the Karate network.
Vertex 4 has a very high significance of 0.97 but
a community disruption of 0. This means that, upon
removing the vertex, nothing changed in the commu-
nity. Whether the vertex exists or not, the commu-
nity remains unchanged. Its high significance how-
ever suggests that its membership is resilient to per-
turbations, which makes sense given that it has 6 in-
ternal connections and no external connections. So
this vertex is a very good representative of a vertex
that has a strong membership to its community but a
low importance for the structure of that community.
Another relevant example is vertex 32, which has
a very low significance (0.56), but a quite high com-
munity disruption (0.09). As discussed previously, its
significance is low probably because of its connec-
tion with a well-connected vertex in another commu-
nity. Removing the vertex causes its community to
split, which indicates that the vertex is important to
the structure of the community. The commitment of
vertex 32 to its own community is not very strong, but
its existence keeps the community together.
There are vertices, such as 34 or 33, which have
both high significance and high disruption. Of course,
some vertices, such as 25, have both low commitment
and low importance to their own communities.
5.2.2 Edge Omission
We applied the same omission method described pre-
viously to the edges of the Karate network in order
to measure their importance. As we can observe in
Figure 10, the edges of highly relevant vertices such
as 24, 33 and 34 are also important. However, there
Figure 10: The Karate network: vertex color intensity is
proportional to significance, vertex size is proportional to
vertex community disruption and edge width is proportional
to edge community disruption.
are vertices with non-zero disruption such as 14, 15
and 16 whose connections have no disruption. What
this tells us is that the removal of the edges of these
vertices as a whole has an impact on the community,
and not the removal of individual edges.
5.3 Vertex Categorization
We propose a generic categorization of vertices into
4 categories based on their commitment and impor-
tance (Table 1). We use significance and community
disruption, but in theory, any measures that quantify
commitment and importance can be used to catego-
rize vertices.
We proceeded and categorized the vertices in the
Karate network based on these criteria. We consider
significance to be high if it is ≥ 0.75 and low if it
is < 0.75. For community disruption, we consid-
ered vertices with 0 disruption to have low impor-
tance, while the rest have high importance. Similar to
our categorization, Guimera and Amaral describe in
(Guimera and Amaral, 2005) a way to assign univer-
sal roles to vertices based on their z-score and partic-
ipation coefficient. Table 2 shows our categorization
compared to the universal roles of these vertices.
We can observe that a few of the vertices fall into
category I, which means they are the most relevant for
their respective communities. A single vertex falls in
category II: 32, which has high importance but low
commitment. Most vertices fall in category III, which
is consistent with our expectations of social networks:
we expect most vertices to have a good commitment
to their own communities, especially since most ver-
tices don’t have external connections, and their im-
portance to be low. We also have a few category IV
vertices, which are the least relevant.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
54

Table 1: Vertex Categories.
Commitment \ Importance High Low
High
Category I:
highly relevant
Category III: committed,
but unimportant
Low
Category II: relevant,
but uncommitted
Category IV:
irrelevant
Table 2: Categories and roles for vertices in the Karate net-
work.
Vertex Cat. Role Vertex Cat. Role
1 I R2 18 III R1
2 III R2 19 III R1
3 I R2 20 III R2
4 III R1 21 III R1
5 III R2 22 III R1
6 III R2 23 III R1
7 III R2 24 I R1
8 III R1 25 IV R1
9 III R2 26 IV R1
10 IV R2 27 III R1
11 III R2 28 II R2
12 IV R1 29 IV R2
13 III R1 30 III R1
14 I R2 31 I R2
15 I R1 32 II R2
16 I R1 33 I R2
17 III R1 34 I R5
Now let us look at how the universal roles com-
pare to our categories. The vertex with both the high-
est significance and importance, 34, is the only hub
and has the “provincial hub” role (R5). Other highly
relevant vertices like 1 and 33 can be promoted to
the R5 role by lowering the z-score threshold, but all
other vertices have either “ultra-peripheral” or “pe-
ripheral” roles (R1 and R2): they have no or very few
external connections so the participation coefficient
tends to be low. Aside from category I vertices, there
does not seem to be a clear correspondence between
our categories and the universal roles, since both pe-
ripheral and ultra-peripheral vertices can have varying
degrees of importance and commitment. One more
thing to note is that since the universal roles are based
on z-score and participation coefficient, two measures
that quantify vertex commitment, they do not take im-
portance into consideration.
Another interesting observation is the relationship
between the community disruption and community
structure disruption of a vertex. As noted before,
community structure disruption ≥ community disrup-
tion and based on the behavior observed in the Karate
network, we can draw the following conclusions:
• If community disruption > 0 and community
disruption = community structure disruption, it
means that upon removal, the community of the
vertex decomposed into sub-communities, the
other communities remaining unaffected.
• If community disruption < community structure
disruption, it means that other communities were
affected by the removal of the vertex and either
lost or gained vertices.
6 CONCLUSIONS
This paper investigates different measures for quanti-
fying the relevance of a vertex in its own community.
We identified two related, but distinct vertex proper-
ties: commitment and importance. Commitment indi-
cates how strongly a vertex belongs to its own com-
munity, while importance shows how relevant a ver-
tex is to that community’s structure. We found that
embeddedness, although easy to compute, does not
carry much information and that significance is better
as a measure for capturing the commitment of a ver-
tex. By comparing significance and embeddedness,
we identified that not only the number of connections
of a vertex is important to its commitment, but also
to which other vertices it is connected to. Based on
this, we were able to propose a new measure, Relative
Commitment, which provides a more accurate estima-
tion of a vertex commitment than embeddedness, yet
is easier to compute than significance.
By removing a vertex from its graph and observ-
ing the changes inside its community and outside (in
the overall community structure), we were able to as-
sess the importance of the vertex, which we identified
as a distinct property to embeddedness. We show that
this strategy is also applicable to edges, to assess their
individual importance.
The community structure of a network offers
much information on the relevance of a vertex. By
Assessing Vertex Relevance based on Community Detection
55
looking at commitment and importance, the most rel-
evant vertices in a community can be identified. To
this end, we proposed a vertex categorization strat-
egy, based on commitment and importance. Knowing
which are the relevant vertices in a network is partic-
ularly of interest in large networks, where extracting
meaningful information is difficult. Potential appli-
cation areas for our methods include social networks,
in which group leaders and influential people can be
identified, or professional networks - determining the
best candidates for hiring. These measures also pro-
vide answers to questions about why a community ex-
ists and what is keeping vertices from leaving a spe-
cific community and joining another one.
We are currently focusing on further investigat-
ing the differences between embeddedness and sig-
nificance in order to identify other factors which in-
fluence the latter. These factors can then be used to
improve the Relative Commitment measure. It would
also be useful to extend the evaluation of these mea-
sures to other types of networks. Alternative, less
computationally intensive measures for assessing ver-
tex importance should also be studied, since vertex
disruption requires the community structure to be re-
computed for each vertex removal.
REFERENCES
Albert, R., Jeong, H., and Barabasi, A. L. (2000). Error
and attack tolerance of complex networks. Nature,
406(6794):378–382.
Fortunato, S. (2010). Community detection in graphs.
Physics Reports, 486(3-5):75–174.
Fortunato, S. and Castellano, C. (2008). Community struc-
ture in graphs. In Encyclopedia of Complexity and
Systems Science, pages 1141–1163.
Guimera, R. and Amaral, L. A. N. (2005). Cartography of
complex networks: modules and universal roles. Jour-
nal of Statistical Mechanics: Theory and Experiment,
2005(P02001):P02001–1–P02001–13.
Karrer, B., Levina, E., and Newman, M. E. J. (2008). Ro-
bustness of community structure in networks. Phys.
Rev. E, 77:046119.
Lancichinetti, A. and Fortunato, S. (2009). Community de-
tection algorithms: a comparative analysis. Phys. Rev.
E, 80:056117.
Lancichinetti, A., Kivela, M., Saramaki, J., and Fortunato,
S. (2010). Characterizing the community structure of
complex networks. CoRR, abs/1005.4376.
Newman, M. E. J. (2003). The structure and function of
complex networks. SIAM REVIEW, 45:167–256.
Newman, M. E. J. (2004). Fast algorithm for detect-
ing community structure in networks. Phys. Rev. E,
69:066133.
Newman, M. E. J. (2006). Finding community structure in
networks using the eigenvectors of matrices. Physical
review E, 74(3).
Orman, G. K., Labatut, V., and Cherifi, H. (2012). Compar-
ative evaluation of community detection algorithms:
A topological approach. Journal of Statistical Me-
chanics: Theory and Experiment, P08001.
Palla, G., Barabasi, A. L., and Vicsek, T. (2007). Quanti-
fying social group evolution. Nature, 446(7136):664–
667.
Rosvall, M. and Bergstrom, C. T. (2008). Maps of random
walks on complex networks reveal community struc-
ture. Proceedings of the National Academy of Sci-
ences, 105(4):1118–1123.
Rosvall, M. and Bergstrom, C. T. (2010). Mapping change
in large networks. PLoS ONE, 5(1):e8694.
Zachary, W. W. (1977). An information flow model for con-
flict and fission in small groups. Journal of Anthropo-
logical Research, 33:452–473.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
56
