A General Schema for Solving Model-Intersection Problems on a
Specialization System by Equivalent Transformation
Kiyoshi Akama
1
and Ekawit Nantajeewarawat
2
1
Information Initiative Center, Hokkaido University, Hokkaido, Japan
2
Computer Science, Sirindhorn International Institute of Technology, Thammasat University, Pathumthani, Thailand
Keywords:
Model-Intersection Problem, Query-Answering Problem, Equivalent Transformation, Problem Solving.
Abstract:
A model-intersection problem (MI problem) is a pair of a set of clauses and an exit mapping. We define MI
problems on specialization systems, which include many useful classes of logical problems, such as proof
problems on first-order logic and query-answering (QA) problems in pure Prolog and deductive databases.
The theory presented in this paper makes clear the central and fundamental structure of representation and
computation for many classes of logical problems by (i) axiomatization and (ii) equivalent transformation.
Clauses in this theory are constructed based on abstract atoms and abstract operation on them, which can be
used for representation of many specific subclasses of problems with concrete syntax. Various computation
can be realized by repeated application of many equivalent transformation rules, allowing many possible
computation procedures, for instance, computation procedures based on resolution and unfolding. This theory
can also be useful for inventing solutions for new classes of logical problems.
1 INTRODUCTION
This paper introduces a model-intersection problem
(MI problem), which is a pair hCs,ϕi, where Cs is a
set of clauses and ϕ is a mapping, called an exit map-
ping, used for constructing the output answer from the
intersection of all models of Cs. More formally, the
answer to a MI problem hCs, ϕi is ϕ(
T
Models(Cs)),
where Models(Cs) is the set of all models of Cs. The
set of all MI problems constitutes a very large class of
problems and is of great importance.
A QA problem is a pair hCs,ai, where Cs is a set
of clauses and a is a user-defined query atom. The
answer to such a QA problem hCs,ai is defined as
the set of all ground instances of a that are logical
consequences of Cs. A QA problem hCs,ai is a MI
problem hCs,ϕ
1
i, where for any set G of ground user-
defined atoms, ϕ
1
(G) is the intersection of G and the
set of all ground instances of a. Characteristically, a
QA problem is an “all-answers finding” problem, i.e.,
all ground instances of a given query atom satisfying
the requirement above are to be found. Many logic
programming languages, including Datalog, Prolog,
and other extensions of Prolog, deal with specific sub-
classes of QA problems.
The class of proof problems is also a subclass of
MI problems. In contrast to a QA problem, a proof
problem, is a “yes/no” problem; it is concerned with
checking whether or not one given logical formula is a
logical consequence of another given logical formula.
Formally, a proof problem is a pair hE
1
,E
2
i, where E
1
and E
2
are first-order formulas, and the answer to this
problem is defined to be “yes” if E
2
is a logical con-
sequence of E
1
, and it is defined to be “no” otherwise.
Historically, proof problems were first solved
(Robinson, 1965). Then QA problems on pure Prolog
were solved based on the resolution principle, which
is a solution for proof problems. This approach is
proof-centered. It has been believed that computa-
tion of Prolog is an inference process. The theory of
SLD resolution was used for the correctness of Pro-
log computation. Many solutions proposed so far for
some other classes of logical problems are also basi-
cally proof-centered.
In contrast, it was shown in (Akama and Nantajee-
warawat, 2013) that the set of all proof problems can
be embedded into the set of all QA problems. This
result supports a QA-centered approach to solving
proof problems, i.e., first, develop a general solution
for QA problems, and then, apply it as a solution for
proof problems (Akama and Nantajeewarawat, 2012).
Since a QA problem is a MI problem (as will be seen
in Theorem 3), we have
PROOF ⊂ QA ⊂ MI,
38
Akama, K. and Nantajeewarawat, E..
A General Schema for Solving Model-Intersection Problems on a Specialization System by Equivalent Transformation.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 2: KEOD, pages 38-49
ISBN: 978-989-758-158-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
where PROOF, QA, and MI denote the class of all
proof problems, the class of all QA problems, and the
class of all MI problems, respectively. The class of
all MI problems is larger than that of all QA prob-
lems, and it is a more natural class to be solved by the
method presented in this paper. A general solution
method for MI problems can be applied to any arbi-
trary QA problem and any arbitrary proof problem.
MI problems are axiomatically constructed on an
abstract structure, called a specialization system. It
consists of abstract atoms and abstract operations
(extensions of variable-substitution operations) on
atoms, called specializations. These abstract com-
ponents can be any arbitrary mathematical objects as
long as they satisfy given axioms. Abstract clauses
can be built on abstract atoms. This is a sharp contrast
to most of the conventional theories in logic program-
ming, where concrete syntax is usually used. In Pro-
log, for example, usual first-order atoms and substi-
tutions with concrete syntax are used, and there is no
way to give a foundation for other forms of extended
atoms and for various specialization operations other
than the usual variable-substitution operation.
An axiomatic theory enables us to develop a very
general theory. By instantiating a specialization sys-
tem to a specific domain and by imposing certain re-
strictions on clauses, our theory can be applied to
many subclasses of MI problems.
We proposed a general schema of solving MI
problems by equivalent transformation (ET), where
problems are solved by repeated simplification. We
introduced the concept of target mapping and pro-
posed three target mappings. Since transformation
preserving a target mapping is ET, target mappings
provide a strong foundation for inventing many ET
rules for solving MI problems on clauses.
An ET-based solution consists of the following
steps: (i) formalize an initial MI problem on some
specialization system, (ii) prepare ET rules, (iii) con-
struct an ET sequence, (iv) compute a set of models
using a target mapping, (v) apply the set-intersection
operation to the resulting set of models, and (vi) apply
an exit mapping to the intersection result to obtain a
solution.
To begin with, Section 2 recalls the concept of
specialization system and formalizes MI problems on
a specialization system. Section 3 defines the notions
of a target mapping and a representative mapping, and
introduces a schema for solving MI problems based
on equivalent transformation (ET) preserving target
mappings. The correctness of this solution schema
is shown. Section 4 applies the general ET-based
schema in Section 3 to the domain of clause sets with
built-in constraint atoms. A target mapping, MM, is
introduced for associating with each clause set a col-
lection of its specific models computed in a bottom-up
manner. Section 5 shows an example of solution of a
MI problem. Section 6 concludes the paper.
The notation that follows holds thereafter. Given
a set A, pow(A) denotes the power set of A and
partialMap(A) the set of all partial mappings on A
(i.e., from A to A). For any partial mapping f from a
set A to a set B, dom( f) denotes the domain of f, i.e.,
dom( f) = {a | (a ∈ A) & ( f(a) is defined)}.
2 CLAUSES AND
MODEL-INTERSECTION
PROBLEMS
2.1 Specialization Systems
A substitution {X/ f(a),Y/g(z)} changes an atom
p(X,5,Y) in the term domain into p( f(a),5,g(z)).
Generally, a substitution in first-order logic defines
a total mapping on the set of all atoms in the term
domain. Composition of such mappings is also re-
alized by some substitution. There is a substitution
that does not change any atom (i.e., the empty sub-
stitution). A ground atom in the term domain is a
variable-free atom.
Likewise, in the string domain, substitutions for
strings are used. A substitution {X/“aYbc”,Y/“xyz”}
changes an atom p(“X5Y”) into p(“aYbc5xyz”).
Such a substitution for strings defines a total mapping
on the set of all atoms that may include string vari-
ables. Composition of such mappings is also realized
by some string substitution. There is a string substi-
tution that does not change any atom (i.e., the empty
substitution). A ground atom in the string domain is a
variable-free atom.
A similar operation can be considered in the
class-variable domain. Consider, for example, an
atom p(X : animal,Y : dog,Z: cat) in this domain,
where X : animal, Y : dog, and Z: cat represent an
animal object, a dog object, and a cat object, re-
spectively. When we obtain additional information
that X is a dog, we can restrict X : animal into
X : dog and the atom p(X : animal,Y : dog,Z: cat)
into p(X : dog,Y : dog,Z: cat). By contrast, with new
information that Z is a dog, we cannot restrict Z : cat
and the above atom since Z cannot be a dog and a cat
at the same time. More generally, such a restriction
operation may not be applicable to some atoms, i.e.,
it defines a partial mapping on the set of all atoms.
Composition of such partial mappings is also a par-
tial mapping, and we can determine some composi-
A General Schema for Solving Model-Intersection Problems on a Specialization System by Equivalent Transformation
39

tion operation corresponding to it. An empty substi-
tution that does not change any atom can be intro-
duced. A ground atom in the class-variable domain is
a variable-free atom.
In order to capture the common properties of such
operations on atoms, the notion of a specialization
system was introduced around 1990.
Definition 1. A specialization system Γ is a quadru-
ple hA,G,S, µi of three sets A, G, and S, and a map-
ping µ from S to partialMap(A) that satisfies the fol-
lowing conditions:
1. (∀s
′
,s
′′
∈ S)(∃s ∈ S ) : µ(s) = µ(s
′
) ◦ µ(s
′′
).
2. (∃s ∈ S)(∀a ∈ A) : µ(s)(a) = a.
3. G ⊆ A.
Elements of A, G, and S are called atoms, ground
atoms, and specializations, respectively. The map-
ping µ is called the specialization operator of Γ. A
specialization s ∈ S is said to be applicable to a ∈ A
iff a ∈ dom(µ(s)).
Assume that a specialization system Γ = hA,G,S,
µi is given. A specialization in S will often be denoted
by a Greek letter such as θ. A specialization θ ∈ S
will be identified with the partial mapping µ(θ) and
used as a postfix unary (partial) operator on A (e.g.,
µ(θ)(a) = aθ), provided that no confusion is caused.
Let ε denote the identity specialization in S , i.e., aε =
a for any a ∈ A. For any θ, σ ∈ S, let θ ◦ σ denote a
specialization ρ ∈ S such that µ(ρ) = µ(σ) ◦ µ(θ), i.e.,
a(θ◦ σ) = (aθ)σ for any a ∈ A.
2.2 User-defined Atoms, Constraint
Atoms, and Clauses
Let Γ
u
= hA
u
,G
u
,S
u
,µ
u
i and Γ
c
= hA
c
,G
c
,S
c
,µ
c
i be
specialization systems such that S
u
= S
c
. Elements
of A
u
are called user-defined atoms and those of G
u
are called ground user-defined atoms. Elements of
A
c
are called constraint atoms and those of G
c
are
called ground constraint atoms. Hereinafter, assume
that S = S
u
= S
c
. Elements of S are called special-
izations. Let TCON denote the set of all true ground
constraint atoms.
A clause on hΓ
u
,Γ
c
i is an expression of the form
a
1
,.. .,a
m
← b
1
,.. .,b
n
,
where m ≥ 0, n ≥ 0, and each of a
1
,.. .,a
m
,b
1
,.. .,b
n
belongs to A
u
∪ A
c
. It is a ground clause on hΓ
u
,Γ
c
i
iff each of a
1
,.. .,a
m
,b
1
,.. .,b
n
belongs to G
u
∪ G
c
.
Let CLS denote the set of all clauses on hΓ
u
,Γ
c
i.
2.3 Interpretations and Models
An interpretation is a subset of G
u
. Unlike ground
user-defined atoms, the truth values of ground con-
straint atoms are predetermined by TCON (cf. Sec-
tion 2.2) independently of interpretations. A ground
constraint atom g is true iff g ∈ TCON. It is false oth-
erwise.
A ground clause C = (a
1
,.. .,a
m
← b
1
,.. .,b
n
) is
true with respect to an interpretation G ⊆ G
u
(in other
words, G satisfies C) iff at least one of the following
conditions is satisfied:
1. There exists i ∈ {1,. .., m} such that a
i
∈ G ∪
TCON.
2. There exists j ∈ {1,. ..,n} such that b
j
/∈ G ∪
TCON.
A clause C is true with respect to an interpretation
G ⊆ G
u
(in other words, G satisfies C) iff for any spe-
cialization θ such that Cθ is ground, Cθ is true with
respect to G. A model of a clause set Cs ⊆ CLS is an
interpretation that satisfies every clause in Cs.
Note that the standard semantics is taken in this
paper, i.e., all models of a formula are considered
instead of specific ones, such as those considered in
the minimal model semantics (Clark, 1978; Lloyd,
1987) (i.e., the semantics underlying logic program-
ming) and those considered in stable model semantics
(Gelfond and Lifschitz, 1988; Gelfond and Lifschitz,
1991) (i.e., the semantics underlying answer set pro-
gramming).
2.4 Model-Intersection (MI) Problems
Let Models be a mapping that associates with each
clause set the set of all of its models, i.e., Models(Cs)
is the set of all models of Cs for any Cs ⊆ CLS.
Assume that a person A and a person B are in-
terested in knowing which atoms in G
u
are true and
which atoms in G
u
are false. They want to know the
unknown set G of all true ground atoms. Due to short-
age of knowledge, A still cannot determine one unique
true subset of G
u
. The person A can only limit possi-
ble subsets of true atoms by specifying a subset Gs
of pow(G
u
). The unknown set G of all true atoms
belongs to Gs. One way for A to inform this knowl-
edge to B compactly is to send to B a clause set Cs
such that Gs ⊆ Models(Cs). Receiving Cs, B knows
that Models(Cs) includes all possible intended sets of
ground atoms, i.e., G ∈ Models(Cs). As such, B can
know that each ground atom outside
S
Models(Cs) is
false, i.e., for any g ∈ G
u
, if g /∈
S
Models(Cs), then
g /∈ G. The person B can also know that each ground
atom in
T
Models(Cs) is true, i.e., for any g ∈ G
u
, if
KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development
40

g ∈
T
Models(Cs), then g ∈ G. This shows the impor-
tance of calculating
T
Models(Cs).
A model-intersection problem (MI problem) is a
pair hCs,ϕi, where Cs ⊆ CLS and ϕ is a mapping from
pow(G
u
) to some set W. The mapping ϕ is called an
exit mapping. The answer to this problem, denoted by
ans
MI
(Cs,ϕ), is defined by
ans
MI
(Cs,ϕ) = ϕ(
\
Models(Cs)),
where
T
Models(Cs) is the intersection of all models
of Cs. Note that when Models(Cs) is the empty set,
T
Models(Cs) = G
u
.
2.5 Query-Answering (QA) Problems
Let Cs ⊆ CLS. For any Cs
′
⊆ CLS, Cs
′
is a logical
consequence of Cs, denoted by Cs |= Cs
′
, iff every
model of Cs is also a model of Cs
′
. For any a ∈ A
u
,
a is a logical consequence of Cs, denoted by Cs |= a,
iff Cs |= {(a ←)}.
A query-answering problem (QA problem) in this
paper is a pair hCs,ai, where Cs ⊆ CLS and a is a
user-defined atom in A
u
. The answer to a QA prob-
lem hCs,ai, denoted by ans
QA
(Cs,a), is defined by
ans
QA
(Cs,a) = {aθ | (θ ∈ S ) & (aθ ∈ G
u
) &
(Cs |= (aθ ←))}.
Theorem 1. For any Cs ⊆ CLS and a ∈ A
u
,
ans
QA
(Cs,a) = rep(a) ∩ (
\
Models(Cs)),
where rep(a) denotes the set of all ground instances
of a.
Proof: Let Cs ⊆ CLS and a ∈ A
u
. By the defi-
nition of |=, for any ground atom g ∈ G
u
, Cs |= g iff
g ∈
T
Models(Cs). Then
ans
QA
(Cs,a)
= {aθ | (θ ∈ S) & (aθ ∈ G
u
) & (Cs |= (aθ ←))}
= {g | (θ ∈ S) & (g = aθ) & (g ∈ G
u
) &
(Cs |= (g ←))}
= {g | (g ∈ rep(a)) & (Cs |= (g ←))}
= {g | (g ∈ rep(a)) & (g ∈ (
T
Models(Cs)))}
= rep(a) ∩ (
T
Models(Cs)).
Theorem 1 shows the importance of the intersec-
tion of all models of a clause set. By this theorem, the
answer to a QA problem can be rewritten as follows:
Theorem 2. Let Cs ⊆ CLS and a ∈ A
u
. Then
ans
QA
(Cs,a) = ans
MI
(Cs,ϕ
1
), where for any G⊆ G
u
,
ϕ
1
(G) = rep(a) ∩ G.
Proof: It follows from Theorem 1 and the defini-
tion of ϕ
1
that ans
QA
(Cs,a) = ϕ
1
(
T
Models(Cs)) =
ans
MI
(Cs,ϕ
1
).
This is one way to regard a QA problem as a MI
problem, which can be understood as follows: The set
T
Models(Cs) often contains too many ground atoms.
The set rep(a) specifies a range of interest in the set
G
u
. The exit mapping ϕ
1
focuses attention on the part
rep(a) by making intersection with it.
Theorem 3 below shows another way to formalize
a QA problem as a MI problem.
Theorem 3. Let Cs ⊆ CLS and a ∈ A
u
. Then
ans
QA
(Cs,a) = ans
MI
(Cs∪ {ans(a) ← a},ϕ
2
), where
for any G ⊆ G
u
, ϕ
2
(G) = {x | ans(x) ∈ G}.
1
Proof: By Theorem 1 and the definition of ϕ
2
,
ans
QA
(Cs,a)
= rep(a) ∩ (
T
Models(Cs))
= ϕ
2
(
T
Models(Cs∪ {ans(a) ← a}))
= ans
MI
(Cs∪ {ans(a) ← a},ϕ
2
).
In logic programming (Lloyd, 1987), a problem
represented by a pair of a set of definite clauses and a
query atom has been intensively discussed. In the de-
scription logic (DL) community (Baader et al., 2007),
a class of problems formulated as conjunctions of
DL-based axioms and assertions together with query
atoms has been discussed (Tessaris, 2001). These two
problem classes can be formalized as subclasses of
QA problems considered in this paper.
3 SOLVING MI PROBLEMS BY
EQUIVALENT
TRANSFORMATION
A general schema for solving MI problems based on
equivalent transformation is formulated and its cor-
rectness is shown (Theorem 8).
3.1 Preservation of Partial Mappings
and Equivalent Transformation
Terminologies such as preservation of partial map-
pings and equivalent transformation are defined in
general below. They will be used with a specific class
of partial mappings called target mappings, which
will be introduced in Section 3.2.
1
The expression ans(a) is not an atom in the usual first-
order logic space. One way to understand Theorem 3 in the
context of the conventional first-order logic is (i) ans(a) is
interpreted as ans(v
1
,...,v
n
), where v
1
,...,v
n
are the vari-
ables occurring in a, and then (ii) ϕ
2
(G) = {x | ans(x) ∈ G}
is interpreted as ϕ
2
(G) = {a
′
| a
′
= ans(t
1
,...,t
n
) ∈ G}.
A General Schema for Solving Model-Intersection Problems on a Specialization System by Equivalent Transformation
41

Assume that X and Y are sets and f is a par-
tial mapping from X to Y. For any x,x
′
∈ dom( f),
transformation of x into x
′
is said to preserve f iff
f(x) = f(x
′
). For any x,x
′
∈ dom( f), transformation
of x into x
′
is called equivalent transformation (ET)
with respect to f iff the transformation preserves f,
i.e., f(x) = f(x
′
).
Let F be a set of partial mappings from a set X
to a set Y. Given x,x
′
∈ X, transformation of x into
x
′
is called equivalent transformation (ET) with re-
spect to F iff there exists f ∈ F such that the trans-
formation preserves f. A sequence [x
0
,x
1
,.. .,x
n
] of
elements in X is called an equivalent transformation
sequence (ET sequence) with respect to F iff for any
i ∈ {0, 1,.. .,n − 1}, transformation of x
i
into x
i+1
is
ET with respect to F. When emphasis is placed on
the initial element x
0
and the final element x
n
, this se-
quence is also referred to as an ET sequence from x
0
to x
n
.
3.2 Target Mappings
Given a MI problem hCs,ϕi, since ans
MI
(Cs,ϕ) =
ϕ(
T
Models(Cs)), the answer to this MI problem is
determined uniquely by Models(Cs) and ϕ. As a re-
sult, we can equivalently consider a new MI prob-
lem with the same answer by switching from Cs to
another clause set Cs
′
if Models(Cs) = Models(Cs
′
).
According to the general terminologies defined
in Section 3.1, on condition that Models(Cs) =
Models(Cs
′
), transformation from x = Cs into x
′
=
Cs
′
preserves f = Models and is called ET with re-
spect to f = Models, where (i) x,x
′
∈ pow(CLS) and
(ii) Models(x),Models(x
′
) ∈ pow(pow(G)). We can
also consider an ET sequence [Cs
0
,Cs
1
,.. .,Cs
n
] of
elements in pow(CLS) with respect to a singleton set
{Models}. MI problems can be transformed into sim-
pler forms by ET preserving Models.
In order to use more partial mappings for simpli-
fication of MI problems, we extend our consideration
from the specific mapping Models to a class of partial
mappings, called GSETMAP, defined below.
Definition 2. GSETMAP is the set of all partial map-
pings from pow(CLS) to pow(pow(G)).
As defined in Section 2.4, Models(Cs) is the set of
all models of Cs for any Cs ⊆ CLS. Since a model is
a subset of G, Models is regarded as a total mapping
from pow(CLS) to pow(pow(G)). Since a total map-
ping is also a partial mapping, the mapping Models is
a partial mapping from pow(CLS) to pow(pow(G)),
i.e., it is an element of GSETMAP.
A partial mapping M in GSETMAP is of par-
ticular interest if
T
M(Cs) =
T
Models(Cs) for any
Cs ∈ dom(M). Such a partial mapping is called a tar-
get mapping.
Definition 3. A partial mapping M ∈ GSETMAP is a
target mapping iff for any Cs ∈ dom(M),
T
M(Cs) =
T
Models(Cs).
It is obvious that:
Theorem 4. The mapping Models is a target map-
ping.
Transformation preserving target mappings and
computation of a target mapping constitute a method
for solving MI problems in this paper.
For more general consideration, we introduce a bi-
nary relation on GSETMAP as follows:
Definition 4. Let M
1
,M
2
∈ GSETMAP. M
1
M
2
iff
the following conditions are satisfied:
1. dom(M
1
) ⊆ dom(M
2
).
2. For any Cs in dom(M
1
),
\
M
1
(Cs) =
\
M
2
(Cs).
Obviously, is reflexive and transitive. It is also
obvious that:
Proposition 1. For any M ∈ GSETMAP, M is a target
mapping iff M Models.
By its definition, a target mapping M satisfies the
following two conditions: (i) the domain of M is a
subset of pow(CLS), and (ii) for any clause set Cs in
the domain of M, the intersection of all ground-atom
sets in M(Cs) is equal to the intersection of all mod-
els of Cs. By the first condition, since the domain of
M can be smaller than that of the mapping Models,
we can expect a more efficient program for comput-
ing M(Cs) for Cs in the domain of M. By the second
condition, the correctness of transformation and com-
putation is guaranteed (Theorems 5 and 8).
Let hCs,ϕi be a MI problem. If M is a target map-
ping such that M(Cs) is defined, then M can be used
for computing the answer to hCs,ϕi. More precisely:
Theorem 5. Let hCs, ϕi be a MI problem and M ∈
GSETMAP. If M is a target mapping and Cs ∈
dom(M), then ans
MI
(Cs,ϕ) = ϕ(
T
M(Cs)).
Proof: Assume that M is a target mapping
and Cs ∈ dom(M). Then
T
M(Cs) =
T
Models(Cs).
Consequently, ans
MI
(Cs,ϕ) = ϕ(
T
Models(Cs)) =
ϕ(
T
M(Cs)).
KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development
42

3.3 Representative Mappings
The relations “smaller than” and “finer than” on
GSETMAP are introduced below.
Definition 5. Let M
1
,M
2
∈ GSETMAP. M
1
is smaller
than M
2
iff the following conditions are satisfied:
1. dom(M
1
) ⊆ dom(M
2
).
2. For any Cs ∈ dom(M
1
), M
1
(Cs) ⊆ M
2
(Cs).
Definition 6. Let M
1
,M
2
∈ GSETMAP. M
1
is finer
than M
2
iff the following conditions are satisfied:
1. dom(M
1
) ⊆ dom(M
2
).
2. For any Cs ∈ dom(M
1
) and any m
2
∈ M
2
(Cs),
there exists m
1
∈ M
1
(Cs) such that m
1
⊆ m
2
.
A smaller target mapping is basically preferable
in order to reduce the cost of computing an answer.
The concept of representative mapping defined below
is useful for constructing small target mappings.
Definition 7. Let M
1
,M
2
∈ GSETMAP. M
1
is a rep-
resentative mapping of M
2
iff the following condi-
tions are satisfied:
1. M
1
is smaller than M
2
.
2. M
1
is finer than M
2
.
Theorem 6. Let M
1
,M
2
∈ GSETMAP. If M
1
is a rep-
resentative mapping of M
2
, then M
1
M
2
.
Proof: Suppose that M
1
is a representative map-
ping of M
2
. Let Cs ∈ dom(M
1
). Since M
1
is smaller
than M
2
, M
1
(Cs) ⊆ M
2
(Cs). Thus
T
M
1
(Cs) ⊇
T
M
2
(Cs). We show that
T
M
1
(Cs) ⊆
T
M
2
(Cs)
as follows: Assume that g ∈
T
M
1
(Cs). Let m
2
∈
M
2
(Cs). Since M
1
is finer than M
2
, there exists
m
1
∈ M
1
(Cs) such that m
1
⊆ m
2
. Since g ∈
T
M
1
(Cs),
g belongs to m
1
. So g ∈ m
2
, and thus, g ∈
T
M
2
(Cs).
It follows that
T
M
1
(Cs) =
T
M
2
(Cs). Hence M
1
M
2
.
3.4 Solving MI Problems by Equivalent
Transformation
Next, a schema for solving MI problems based
on equivalent transformation (ET) preserving target
mappings is formulated. The notions of preservation
of target mappings, ET with respect to target map-
pings, and an ET sequence are obtained by specializ-
ing the general definitions in Section 3.1.
Let π be a mapping, called state mapping, from a
given set STATE to the set of all MI problems. Ele-
ments of STATE are called states.
Definition 8. Let hS,S
′
i ∈ STATE× STATE. hS,S
′
i is
an ET step with π iff if π(S) = hCs,ϕi and π(S
′
) =
hCs
′
,ϕ
′
i, then ans
MI
(Cs,ϕ) = ans
MI
(Cs
′
,ϕ
′
).
Definition 9. A sequence [S
0
,S
1
,.. .,S
n
] of elements
of STATE is an ET sequence with π iff for any i ∈
{0,1,.. .,n− 1}, hS
i
,S
i+1
i is an ET step with π.
We can construct an ET step by using transfor-
mation preserving a target mapping. ET steps used
for solving MI problems are mainly realized based on
target mappings.
Theorem 7. Let S, S
′
∈ STATE. Assume that π(S) =
hCs,ϕi, π(S
′
) = hCs
′
,ϕi, and M is a target mapping
such that M(Cs) = M(Cs
′
). Then hS,S
′
i is an ET step
with π.
Proof:
ans
MI
(Cs,ϕ)
= ϕ(
T
Models(Cs))
= (since M is a target mapping)
= ϕ(
T
M(Cs))
= (since M(Cs) = M(Cs
′
))
= ϕ(
T
M(Cs
′
))
= (since M is a target mapping)
= ϕ(
T
Models(Cs
′
))
= ans
MI
(Cs
′
,ϕ)
As shown below, we can solve MI problems by
constructing ET sequences.
Theorem 8. Assume that:
• hCs,ϕi is a MI problem.
• [S
0
,S
1
,.. .,S
n
] is an ET sequence with π.
• π(S
0
) = hCs,ϕi and π(S
n
) = hCs
n
,ϕ
n
i.
• M is a target mapping such that Cs
n
∈ dom(M).
Then ans
MI
(Cs,ϕ) = ϕ
n
(
T
M(Cs
n
)).
Proof:
ans
MI
(Cs,ϕ)
= ϕ(
T
Models(Cs))
= (since [S
0
,S
1
,.. .,S
n
] is an ET sequence)
= ϕ
n
(
T
Models(Cs
n
))
= (since M is a target mapping)
= ϕ
n
(
T
M(Cs
n
)).
4 TARGET MAPPINGS FOR
CLAUSES AND COMPUTATION
Next, three target mappings are introduced, i.e., τ
1
for sets of positive unit clauses, τ
2
for sets of defi-
nite clauses, and MM for sets of arbitrary clauses in
A General Schema for Solving Model-Intersection Problems on a Specialization System by Equivalent Transformation
43

CLS. Based on these target mappings, an ET solution
for MI problems on clauses is given according to the
general schema of Section 3.
4.1 A Target Mapping for Sets of
Positive Unit Clauses
A positive unit clause is a clause of the form (a ←),
where a is a user-defined atom. Let PUCL denote the
set of all positive unit clauses. For any user-defined
atom a, let rep(a) denote the set of all ground in-
stances of a.
A partial mapping τ
1
∈ GSETMAP is defined as
follows:
1. For any F ⊆ PUCL, τ
1
(F) is the singleton set
{
S
{rep(a) | (a ←) ∈ F}}.
2. For any Cs ⊆ CLS such that Cs 6⊆ PUCL, τ
1
(Cs)
is undefined.
Theorem 9. τ
1
is a representative mapping of Models
and is a target mapping.
Proof: Assume that F ⊆ PUCL. Let m
F
=
S
{rep(a) | (a ←) ∈ F}. Obviously, m
F
is a model
of F, i.e., m
F
∈ Models(F). So τ
1
is smaller than
Models. Now let m ∈ Models(F). For any (a ←) ∈ F
and any g ∈ rep(a), g is true with respect to m, i.e.,
g ∈ m. Then m
F
⊆ m. So τ
1
is also finer than Models,
whence τ
1
is a representative mapping of Models. By
Theorem 6 and Proposition 1, τ
1
is a target map-
ping.
4.2 A Target Mapping for Sets of
Definite Clauses
A definite clause is a clause whose left-hand side con-
tains exactly one user-defined atom and no constraint
atom. Let DCL denote the set of all definite clauses.
Given a definite clause C, the atom in the left-hand
side ofC is called the head of C, denoted by head(C),
and the set of all user-defined atoms and constraint
atoms in the right-hand side of C is called the body
of C, denoted by body(C). Assume that D is a set of
definite clauses in DCL. The meaning of D, denoted
by M (D), is defined as follows:
1. A mapping T
D
on pow(G) is defined by: for any
set G ⊆ G, T
D
(G) is the set
{head(Cθ) | (C ∈ D) & (θ ∈ S) &
(each user-defined atom in body(Cθ) is in G) &
(each constraint atom in body(Cθ) is true)}.
2. M (D) is then defined as the set
S
∞
n=1
T
n
D
(∅),
where T
1
D
(∅) = T
D
(∅) and for each n > 1, T
n
D
(∅)
= T
D
(T
n−1
D
(∅)).
Then a partial mapping τ
2
∈ GSETMAP is defined
below.
1. For any D ⊆ DCL, τ
2
(D) is the singleton set
{M (D)}.
2. For any Cs ⊆ CLS such that Cs 6⊆ DCL, τ
2
(Cs) is
undefined.
Theorem 10. τ
2
is a representative mapping of
Models and is a target mapping.
Proof: Let D ⊆ DCL. Since M (D) is a model
of D, {M (D)} ⊆ Models(D). So τ
2
is smaller than
Models. Let m ∈ Models(D). Since M (D) is the least
model of D, M (D) ⊆ m. So τ
2
is finer than Models.
Then τ
2
is a representative mapping of Models, and
thus, by Theorem 6 and Proposition 1, it is a target
mapping.
Theorem 11. For any F ⊆ PUCL, τ
2
(F) = τ
1
(F).
Proof: For any F ⊆ PUCL, τ
2
(F) = {M (F)} =
{
S
{rep(a) | (a ←) ∈ F}} = τ
1
(F).
4.3 A Target Mapping for Clause Sets
Given a clauseC, the set of all user-defined atoms and
constraint atoms in the left-hand side of C is denoted
by lhs(C) and the set of all those in the right-hand
side of C is denoted by rhs(C). A clause C is said
to be positive if lhs(C) is not empty; it is said to be
negative otherwise.
It is assumed henceforth that (i) for any constraint
atom c, not(c) is a constraint atom; (ii) for any con-
straint atom c and any specialization θ, not(c)θ =
not(cθ); and (iii) for any ground constraint atom c,
c is true iff not(c) is not true.
The following notation is used for defining a tar-
get mapping MM for arbitrary clauses in CLS (Defi-
nition 10).
1. Let Cs be a set of clauses possibly with con-
straint atoms. MVRHS(Cs) is defined as the set
{MVRHS(C) | C ∈ Cs}, where for any clause C ∈
Cs, MVRHS(C) is the clause obtained from C as
follows: For each constraint atom c in lhs(C), re-
move c from lhs(C) and add not(c) to rhs(C).
2. Let Cs be a set of clauses with no constraint
atom in their left-hand sides. For any G ⊆ G,
GINST(Cs,G) is defined as the set
{RMCON(Cθ) | (C ∈ Cs) & (θ ∈ S) &
(each user-defined atom in Cθ is in G) &
(each constraint atom in rhs(Cθ) is true)},
KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development
44

where for any clause C
′
, RMCON(C
′
) is the clause
obtained fromC
′
by removing all constraint atoms
from it.
3. Let Cs be a set of clauses possibly with constraint
atoms. For any G ⊆ G, INST(Cs,G) is defined by
INST(Cs,G) = GINST(MVRHS(Cs), G).
4. Let Cs be a set of ground clauses with no con-
straint atom. We can construct a set of defi-
nite clauses from Cs as follows: For each clause
C ∈ Cs,
• if lhs(C) = ∅, then construct a definite clause
the head of which is ⊥ and the body of which
is rhs(C), where ⊥ is a special symbol not oc-
curring in Cs;
• if lhs(C) 6= ∅, then (i) select one arbitrary atom
a from lhs(C), and (ii) construct a definite
clause the head of which is a and the body of
which is rhs(C).
Let DC(Cs) denote the set of all definite-clause
sets possibly constructed from Cs in the above
way.
Proposition 2. Let Cs ⊆ CLS. For any m ⊆ G, m is a
model of Cs iff m is a model of INST(Cs,G).
Proof: INST(Cs,G) is obtained from Cs by (i)
moving constraint atoms in the left-hand sides of
clauses into their right-hand sides, (ii) instantiation of
variables into ground terms, (iii) removal of clauses
containing false constraint atoms in their right-hand
sides, and (iv) removal of true constraint atoms from
the remaining clauses. Each of the operations (i), (ii),
(iii), and (iv) preserves models.
A mapping MM is defined below.
Definition 10. A mapping MM ∈ GSETMAP is de-
fined by
MM(Cs) = {M (D) | (D ∈ DC(INST(Cs, G))) &
(⊥ /∈ M (D))}
for any Cs ⊆ CLS.
Theorem 12. MM is a representative mapping of
Models and is a target mapping.
Proof: First, we show that MM is smaller than
Models. Let Cs ⊆ CLS. Suppose that m ∈ MM(Cs).
Let Cs
′
= INST(Cs,G). Then there exists D such that
m = M (D), D ∈ DC(Cs
′
), and ⊥ /∈ M (D). We show
that m is a model of Cs
′
as follows:
• Let C
P
be a positive clause in Cs
′
. Since D ∈
DC(Cs
′
), there exists C ∈ D such that head(C) ∈
lhs(C
P
) and body(C) = rhs(C
P
). Since m satis-
fies C, m also satisfies C
P
. Hence m satisfies every
positive clause in Cs
′
.
• Let C
N
be a negative clause in Cs
′
. Since D ∈
DC(Cs
′
), there existsC
′
∈ D such that head(C
′
) =
⊥ and body(C
′
) = rhs(C
N
). Since ⊥ /∈ M (D),
m does not include body(C
′
). So rhs(C
N
) 6⊆ m,
whence m satisfies C
N
. Hence m satisfies every
negative clause in Cs
′
.
So m is a model of Cs
′
. By Proposition 2, m is a model
of Cs, i.e., m ∈ Models(Cs).
Next, we show that MM is finer than Models. Let
Cs ⊆ CLS. Suppose that m
′
∈ Models(Cs), i.e., m
′
is
a model of Cs. Let Cs
′
= INST(Cs, G). By Propo-
sition 2, m
′
is also a model of Cs
′
. Let D be a set
of definite clauses obtained from Cs
′
by constructing
from each positive clause C in Cs
′
a definite clause C
′
as follows:
1. Select an atom a from lhs(C) as follows:
(a) If rhs(C) ⊆ m
′
, then select an atom a ∈ lhs(C) ∩
m
′
.
(b) If rhs(C) 6⊆ m
′
, then select an arbitrary atom a ∈
lhs(C).
2. Construct C
′
as a definite clause such that
head(C
′
) = a and body(C
′
) = rhs(C).
It is obvious that m
′
is a model of D. Let m
′′
= M (D).
Since m
′′
is the least model of D, m
′′
⊆ m
′
. Since
m
′
is a model of Cs
′
, m
′
satisfies all negative clauses
in Cs
′
. Since m
′′
⊆ m
′
, m
′′
also satisfies all negative
clauses in Cs
′
. It followsthat ⊥ /∈ M (D). Hence m
′′
∈
MM(Cs).
So MM is a representative mapping of Models.
By Theorem 6 and Proposition 1, MM is a target map-
ping.
Theorem 13. For any D ⊆ DCL, MM(D) = τ
2
(D).
Proof: Let D ⊆ DCL. Then DC(INST(D,G)) is
the singleton set {INST(D,G)}. Obviously, M (D) =
M (INST(D,G)) and ⊥ /∈ M (INST(D, G)). It follows
that
MM(D) = {M (D
′
) | (D
′
∈ DC(INST(D,G))) &
(⊥ /∈ M (D
′
))}
= {M (INST(D,G))}
= {M (D)}
= τ
2
(D).
A General Schema for Solving Model-Intersection Problems on a Specialization System by Equivalent Transformation
45
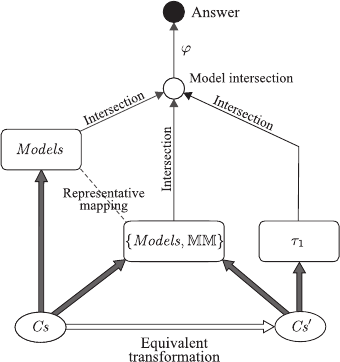
Figure 1: Target mappings and ET computation paths.
4.4 Computation Cost for Solving MI
Problems
Given a set Cs of clauses, a user-defined atom a, and
an exit mapping ϕ, the answer to the MI problem
hCs,ϕi, i.e., ans
MI
(Cs,ϕ) = ϕ(
T
Models(Cs)), can be
directly obtained by the computation shown in the
leftmost path in Fig. 1.
By Theorems 4, 9, and 12, each of Models, τ
1
, and
MM is a target mapping. By Theorem 8, with M = τ
1
,
ans
MI
(Cs,ϕ) can be obtained as follows:
1. Construct S
0
= hCs,ϕi.
2. Construct an ET sequence based on Models and
MM starting with S
0
and ending with S
n
=
hCs
n
,ϕ
n
i such that Cs
n
∈ dom(τ
1
).
3. ans
MI
(Cs,ϕ) = ϕ
n
(
T
τ
1
(Cs
n
)).
For the discussion below, the following notation is
assumed:
• For any S, S
′
∈ STATE, let trans(S,S
′
) denote the
transformation of S into S
′
, and time(trans(S, S
′
))
denote the computation time required for this
transformation step.
• Let π be a state mapping. For any target mapping
τ and S ∈ STATE, let comp(τ,S) denote the com-
putation of ϕ(
T
τ(Cs)), where π(S) = hCs, ϕi, and
let time(comp(τ,S)) denote the amount of time re-
quired for this computation.
Using this notation, the time of the above solution by
the ET sequence [S
0
,S
1
,.. .,S
n
] with τ
1
above is eval-
uated by
T
τ
1
= Σ
n
i=1
time(trans(S
i−1
,S
i
)) + time(comp(τ
1
,S
n
)).
By the definition of τ
1
, time(comp(τ
1
,S
n
)) is very
small. Assuming each transformation step in the ET
C
1
: FM(x) ← FP(x)
C
2
: FP(john) ←
C
3
: FP(mary) ←
C
4
: teach(john,ai) ←
C
5
: St(paul) ←
C
6
: AC(ai) ←
C
7
: Tp(kr) ←
C
8
: Tp(lp) ←
C
9
: curr(x,z) ← exam(x,y),subject(y,z),St(x),
Co(y),Tp(z)
C
10
: mayDoThesis(x,y) ← curr(x,z),expert(y,z),
St(x),Tp(z),FP(y),
AC(w),teach(y,w)
C
11
: mayDoThesis(x,y) ← St(x),NFP(y)
C
12
: exam(paul,ai) ←
C
13
: subject(ai,kr) ←
C
14
: subject(ai,lp) ←
C
15
: expert(john,kr) ←
C
16
: expert(mary,lp) ←
C
17
: AC(x) ← teach(mary,x)
C
18
: ← AC(x),BC(x)
C
19
: AC(x),BC(x) ← Co(x)
C
20
: Co(x) ← AC(x)
C
21
: Co(x) ← BC(x)
C
22
: FP(x) ← NFP(x)
C
23
: ← NFP(x),teach(x,y),Co(y)
C
24
: teach(y, x),NFP(y) ← FP(y),funcf
0
(y,x)
C
25
: Co(x),NFP(y) ← FP(y),funcf
0
(y,x)
C
26
: funcf
0
(john,ai) ←
C
27
: ← funcf
0
(mary,ai)
Figure 2: Clauses representing the background knowledge
of the modified mayDoThesis problem.
sequence from S
0
to S
n
is also very small, the value
T
τ
1
is small enough and the solution by this ET se-
quence with τ
1
can be efficient. This is a basic strat-
egy to obtain an efficient solution for a MI problem.
In order to use τ
1
after repeated equivalent
transformation, the clause set Cs
n
determined by
π(S
n
), where S
n
is the final state obtained from
the ET sequence [S
0
,S
1
,.. .,S
n
], must be inside
dom(τ
1
). In other words, the role of the ET sequence
[S
0
,S
1
,.. .,S
n
] is to construct Cs
n
that enters dom(τ
1
)
starting from S
0
.
5 EXAMPLE
Usual first-order atoms are used for illustration be-
low. To apply the proposed theory in this section,
a specialization system hA
u
,G
u
,S, µ
u
i corresponding
to the usual first-order space is used, where A
u
is the
set of all first-order atoms, G
u
is the set of all ground
first-order atoms, S is the set of all substitutions on
KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development
46

A
u
, and µ
u
provides the specialization operation cor-
responding to the usual application of substitutions in
S to atoms in A
u
.
5.1 Problem Description
Let Cs be the set consisting of the clauses C
1
–
C
27
in Fig. 2. These clauses are obtained from
the mayDoThesis problem given in (Donini et al.,
1998) with some modification.
2
All atoms ap-
pearing in Fig. 2 belong to A
u
. The unary pred-
icates NFP, FP, FM, Co, AC, BC, St, and Tp
denote “non-teaching full professor,” “full profes-
sor,” “faculty member,” “course,” “advanced course,”
“basic course,” “student,” and “topic,” respectively.
The clauses C
9
–C
11
together provide the conditions
for a student to do his/her thesis with a profes-
sor, where mayDoThesis(s, p), curr(s,t), expert(p,t),
exam(s,c), and subject(c,t) are intended to mean “s
may do his/her thesis with p,” “s studied t in his/her
curriculum,” “p is an expert in t,” “s passed the exam
of c,” and “c covers t,” respectively, for any student s,
any professor p, any topic t, and any course c.
Let a be the atom mayDoThesis(paul,x). We con-
sider the QA problem hCs,ai, which is to find all stu-
dents who may do their theses with paul. Let ϕ be
defined by: for any G ⊆ G
u
,
ϕ(G) = {mayDoThesis(paul, x) | ans(x) ∈ G},
where ans is a unary predicate denoting “answer.”
The QA problem hCs,ai above can then be trans-
formed into a MI problem hCs ∪ {C
0
},ϕi, where C
0
is the clause given by:
C
0
: ans(x) ← mayDoThesis(paul,x)
Using rules for transformation of clauses given
in Sections 5.2–5.4, how to compute the answer to
the MI problem hCs ∪ {C
0
},ϕi is illustrated in Sec-
tion 5.5.
5.2 Unfolding Operation
Assume that:
• Cs ⊆ CLS.
• D is a set of definite clauses in CLS.
• occ is an occurrence of an atom b in the right-hand
side of a clause C in Cs.
2
To represent the original mayDoThesis problem in a
clausal form, extended clauses with function variables are
used. To change atoms with function variables into user-
defined atoms, the funcf
0
predicate is used in the clauses
C
24
–C
27
.
By unfolding Cs using D at occ, Cs is transformed
into
(Cs− {C}) ∪ (
[
{resolvent(C,C
′
,b) | C
′
∈ D}),
where for each C
′
∈ D, resolvent(C,C
′
,b) is defined
as follows, assuming that ρ is a renaming substitution
for usual variables such that C and C
′
ρ have no usual
variable in common:
1. If b and head(C
′
ρ) are not unifiable, then
resolvent(C,C
′
,b) = ∅.
2. If they are unifiable, then
resolvent(C,C
′
,b) = {C
′′
},
where C
′′
is the clause obtained from C and C
′
ρ
as follows, assuming that θ is the most general
unifier of b and head(C
′
ρ):
(a) lhs(C
′′
) = lhs(Cθ)
(b) rhs(C
′′
) = (rhs(Cθ) − {bθ}) ∪ body(C
′
ρθ)
The resulting clause set is denoted by UNFOLD(Cs,
D,occ).
5.3 ET by Unfolding and Definite-clause
Removal
For any predicate p, let Atoms(p) denote the set of
all atoms having the predicate p. Equivalent trans-
formation (ET) of clauses using unfolding and using
definite-clause removal are formulated below.
Theorem 14. Let Cs ⊆ CLS and a ∈ A
u
. Assume that:
1. q is the predicate of the query atom a.
2. p is a predicate such that p 6= q.
3. D is a set of definite clauses in Cs that satisfies the
following conditions:
(a) For any definite clause C ∈ D,
head(C) ∈ Atoms(p).
(b) For any clause C
′
∈ Cs− D,
lhs(C
′
) ∩ Atoms(p) = ∅.
4. occ is an occurrence of an atom in Atoms(p) in
the right-hand side of a clause in Cs− D.
Then the following two sets are equal:
• (
T
Models(Cs)) ∩ rep(a)
• (
T
Models(UNFOLD(Cs,D,occ))) ∩ rep(a).
Theorem 15. Let Cs ⊆ CLS and a ∈ A
u
. Assume that:
1. q is the predicate of the query atom a.
A General Schema for Solving Model-Intersection Problems on a Specialization System by Equivalent Transformation
47

2. p is a predicate such that p 6= q.
3. D is a set of definite clauses in Cs that satisfies the
following conditions:
(a) For any definite clause C ∈ D,
head(C) ∈ Atoms(p).
(b) For any clause C
′
∈ Cs− D,
lhs(C
′
) ∩ Atoms(p) = ∅.
4. For any clause C
′
∈ Cs− D,
rhs(C
′
) ∩ Atoms(p) = ∅.
Then the following two sets are equal:
• (
T
Models(Cs)) ∩ rep(a)
• (
T
Models(Cs− D)) ∩ rep(a)
5.4 Other Transformations
5.4.1 Elimination of Subsumed Clauses and
Elimination of Valid Clauses
A clause C
1
is said to subsume a clause C
2
iff there
exists a substitution θ for usual variables such that
lhs(C
1
)θ ⊆ lhs(C
2
) and rhs(C
1
)θ ⊆ rhs(C
2
). If a
clause set Cs contains clauses C
1
and C
2
such that
C
1
subsumes C
2
, then Cs can be transformed into
Cs− {C
2
}.
A clause is valid iff all of its ground instances are
true. Given a clause C, if some atom in rhs(C) be-
longs to lhs(C), then C is valid. A valid clause can be
removed.
5.4.2 Side-change Transformation
Assume that p is a predicate occurring in a clause
set Cs and p does not appear in a query atom under
consideration. The clause set Cs can be transformed
by changing the clause sides of p-atoms as follows:
First, determine a new predicate notp for p. Next,
move all p-atoms in each clause to their opposite side
in the same clause (i.e., from the left-hand side to the
right-hand side and vice versa) with their predicates
being changed from p to notp. Side-change transfor-
mation is useful for decreasing the number of atoms
in a multi-head clause (i.e., a clause whose left-hand
side contains more than one atom) in Cs when (i) ev-
ery negative clause in Cs has at most one p-atom in
its right-hand side and (ii) every non-negative clause
in Cs has more p-atoms in its left-hand side than those
in its right-hand side.
C
28
: teach(john,ai) ←
C
29
: AC(ai) ←
C
30
: AC(x) ← teach(mary,x)
C
31
: ← AC(x),BC(x)
C
32
: AC(x),BC(x) ← Co(x)
C
33
: Co(x) ← AC(x)
C
34
: Co(x) ← BC(x)
C
35
: ← NFP(x),teach(x,y),Co(y)
C
36
: ans(y) ← NFP(x)
C
37
: ans(john) ← AC(x),teach(john,x),Co(ai)
C
38
: ans(mary) ← AC(x),teach(mary,x),Co(ai)
C
39
: ans(john) ← AC(x),teach(john,x),
NFP(john),Co(ai)
C
40
: ans(mary) ← AC(x),teach(mary,x),
NFP(mary),Co(ai)
C
41
: teach(john,ai),NFP(john) ←
C
42
: Co(ai),NFP(john) ←
Figure 3: Clauses obtained by application of unfolding and
application of basic transformation rules.
C
43
: ans(x),notNFP(x) ←
C
44
: notNFP(john) ←
C
45
: ans(john) ←
C
46
: ← BC(ai)
Figure 4: Clauses obtained by further application of trans-
formation rules.
5.5 ET Computation
The clause set Cs∪ {C
0
}, consisting of C
0
–C
27
, given
in Section 5.1 is transformed using ET rules provided
by Sections 5.2–5.4 as follows:
• By (i) unfolding using the definitions of the predi-
cates mayDoThesis, FP, Tp, curr, subject, expert,
St, exam, funcf
0
, and FM, (ii) removing these def-
initions using definite-clause removal, and (iii) re-
moval of valid clauses, the clauses C
0
–C
27
are
transformed into the clauses C
28
–C
42
in Fig. 3.
• Side-change transformation for NFP enables (i)
unfolding using the definitions of teach, Co,
and AC, (ii) elimination of these definitions us-
ing definite-clause removal, (iii) removal of valid
clauses, and (iv) elimination of subsumed clauses.
By such side-change transformation followed by
transformation of these four types, C
28
–C
42
are
transformed into the clauses C
43
–C
46
in Fig. 4.
• Side-change transformation for notNFP enables
unfolding using the definitions of BC and NFP.
By unfolding and definite-clause removal, C
43
–
C
46
are transformed into C
45
, i.e., (ans(john) ←).
As a result, the MI problem hCs∪ {C
0
},ϕi in Sec-
tion 5.1 is transformed equivalently into the MI prob-
lem h{(ans(john) ←)},ϕi. Hence
KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development
48
ans
MI
(Cs∪ {C
0
},ϕ)
= ans
MI
({(ans(john) ←)},ϕ)
= ϕ(
T
Models({(ans(john) ←)}))
= {mayDoThesis(paul,john)}.
6 CONCLUSIONS
A model-intersection problem (MI problem) is a pair
hCs,ϕi, where Cs is a set of clauses and ϕ is an exit
mapping used for constructing the output answer from
the intersection of all models of Cs. The proposed
ET-based solution for MI problems consists of the fol-
lowing steps: (i) formalize a given problem as an MI
problem on some specialization system, (ii) prepare
ET rules from clauses, (iii) construct an ET sequence,
(iv) compute a set of models using a target mapping,
(v) apply the set-intersection operation to the result-
ing set of models, and (vi) apply an exit mapping to
the intersection result to obtain a solution.
The class of MI problems considered in this pa-
per has many parameters, such as abstract atoms, spe-
cializations, restriction on forms of clauses, etc. By
instantiating these parameters, we can obtain theories
for subclasses of QA and proof problems correspond-
ing to conventionalclause-based theories, such as dat-
alog, Prolog, and many other extensions of Prolog.
We introduced the concept of target mapping and
proposed three target mappings, i.e., τ
1
for sets of
positive unit clauses, τ
2
for sets of definite clauses,
and MM for arbitrary sets of clauses. These target
mappings provide a strong foundation for inventing
many ET rules for solving MI problems on clauses.
Most kinds of ET rules, including the resolution and
factoring ET rules, are realized by transformations
that preserve these target mappings. For instance,
a proof based on the resolution principle can be re-
garded as ET computation using the resolution and
factoring ET rules. By introducing new ET rules, we
can devise a new proof method (Akama and Nantajee-
warawat, 2013). By inventing additional ET rules, we
have been successful in solving a large class of QA
problems (Akama and Nantajeewarawat, 2014).
By instantiation, the class of MI problems on spe-
cialization systems produces, among others, one of
the largest classes of logical problems with first-order
atoms and substitutions. The ET solution has been
proved to be very general and fundamental since its
correctness for such a large class of problems has
been shown in this paper. By its generality, the theory
developed in this paper makes clear the fundamental
and central structure of representation and computa-
tion for logical problem solving.
ACKNOWLEDGEMENTS
This research was partially supported by JSPS KAK-
ENHI Grant Numbers 25280078 and 26540110.
REFERENCES
Akama, K. and Nantajeewarawat, E. (2012). Proving Theo-
rems Based on Equivalent Transformation Using Res-
olution and Factoring. In Proceedings of the Second
World Congress on Information and Communication
Technologies, WICT 2012, pages 7–12, Trivandrum,
India.
Akama, K. and Nantajeewarawat, E. (2013). Embedding
Proof Problems into Query-Answering Problems and
Problem Solving by Equivalent Transformation. In
Proceedings of the 5th International Conference on
Knowledge Engineering and Ontology Development,
pages 253–260, Vilamoura, Portugal.
Akama, K. and Nantajeewarawat, E. (2014). Equiva-
lent Transformation in an Extended Space for Solv-
ing Query-Answering Problems. In Proceedings of
the 6th Asian Conference on Intelligent Information
and Database Systems, LNAI 8397, pages 232–241,
Bangkok, Thailand.
Baader, F., Calvanese, D., McGuinness, D. L., Nardi, D.,
and Patel-Schneider, P. F., editors (2007). The De-
scription Logic Handbook. Cambridge University
Press, second edition.
Clark, K. L. (1978). Negation as Failure. In Gallaire, H.
and Minker, J., editors, Logic and Data Bases, pages
293–322. Plenum Press, New York.
Donini, F. M., Lenzerini, M., Nardi, D., and Schaerf, A.
(1998). AL-log: Integrating Datalog and Description
Logics. Journal of Intelligent Information Systems,
16:227–252.
Gelfond, M. and Lifschitz, V. (1988). The Stable Model
Semantics for Logic Programming. In Proceedings
of International Logic Programming Conference and
Symposium, pages 1070–1080. MIT Press.
Gelfond, M. and Lifschitz, V. (1991). Classical Negation
in Logic Programs and Disjunctive Databases. New
Generation Computing, 9:365–386.
Lloyd, J. W. (1987). Foundations of Logic Programming.
Springer-Verlag, second, extended edition.
Robinson, J. A. (1965). A Machine-Oriented Logic Based
on the Resolution Principle. Journal of the ACM,
12:23–41.
Tessaris, S. (2001). Questions and Answers: Reasoning and
Querying in Description Logic. PhD thesis, Depart-
ment of Computer Science, The University of Manch-
ester, UK.
A General Schema for Solving Model-Intersection Problems on a Specialization System by Equivalent Transformation
49
