Clustering Stability and Ground Truth: Numerical Experiments
Maria José Amorim
1
and Margarida G. M. S. Cardoso
2
1
Dep. of Mathematics, ISEL and Inst. Univ. de Lisboa (ISCTE-IUL), BRU-IUL, Av. Forças Armadas, Lisboa, Portugal
2
Dep. of Quantitative Methods and BRU-UNIDE, ISCTE Busines School-IUL, Av. das Forças Armadas, Lisboa, Portugal
Keywords: Clustering, External Validation, Stability.
Abstract: Stability has been considered an important property for evaluating clustering solutions. Nevertheless, there
are no conclusive studies on the relationship between this property and the capacity to recover clusters
inherent to data (“ground truth”). This study focuses on this relationship resorting to synthetic data
generated under diverse scenarios (controlling relevant factors). Stability is evaluated using a weighted
cross-validation procedure. Indices of agreement (corrected for agreement by chance) are used both to
assess stability and external validation. The results obtained reveal a new perspective so far not mentioned
in the literature. Despite the clear relationship between stability and external validity when a broad range of
scenarios is considered, within-scenarios conclusions deserve our special attention: faced with a specific
clustering problem (as we do in practice), there is no significant relationship between stability and the
ability to recover data clusters.
1 INTRODUCTION
Stability has been recognized as a desirable property
of a clustering solution – e.g., (Jain and Dubes,
1988). A clustering solution is said to be stable if it
remains fairly unchanged when the clustering
process is subject to minor modifications such as
alternative parameterizations of the algorithm used,
introducing noise in the data or considering different
samples. In order to evaluate stability, the agreement
between the different clustering results originated by
such minor modifications should be measured.
Several indices of agreement (IA), such as the
adjusted Rand (Hubert and Arabie, 1985), are
commonly used for this end.
Some authors warn of a possible misuse of the
property of clustering stability noting that the
goodness of this property in the evaluation of
clustering results is not theoretically well founded:
“While it is a reasonable requirement that an
algorithm should demonstrate stability in general, it
is not obvious that, among several stable algorithms,
the one which is most stable leads to the best
performance” – ((Ben-David and Luxburg, 2008),
p.1.) Bubeck et al., express a similar concern:
“While model selection based on clustering stability
is widely used in practice, its behavior is still not
well-understood from a theoretical point of view”-
((Bubeck et al., 2012), p.436). Therefore, this study
on clustering stability aims to contribute to clarify
the role of this property in the evaluation of
clustering results.
We focus on the relationship between clustering
stability and its external validity i.e. agreement with
“ground truth” – the true clusters’ structures that are
“a priori” known. Our aim is to obtain new insights
based on diverse experimental scenarios.
We analyze diverse clustering results referred to
540 synthetic data sets generated under 18 different
scenarios. Synthetic data sets provide straight-
forward clustering external evaluation and enable to
control for diverse relevant factors such as the
number of clusters, balance and overlapping – e.g.,
(Milligan and Cooper, 1985), (Vendramin et al.,
2010), (Chiang and Mirkin, 2010).
2 THE PROPOSED METHOD
2.1 Why Stability?
Clustering stability, along with cohesion-separation,
are commonly referred as a desirable properties of a
clustering solution.
Cohesion-separation is intrinsically related with
the concept of clustering and it can be related with
the clusters' external validity - Milligan and Cooper
Amorim, M. and Cardoso, M..
Clustering Stability and Ground Truth: Numerical Experiments.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 1: KDIR, pages 259-264
ISBN: 978-989-758-158-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
259
(Milligan and Cooper, 1985) and Vendramin
(Vendramin et al., 2010).
The value of stability is clearly related with the
need to provide a useful clustering solution, since an
inconsistent one would hardly serve practical
purposes. On the other hand, the theoretical value of
stability is yet to be understood.
Literature contributions on stability are discussed
in Luxburg (Luxburg, 2009) and Ben-David and
Luxburg (Ben-David and Luxburg, 2008), for
example. These are specifically related with the
capacity to recover the "right" number of clusters
and to K-Means results. Another perspective of
stability is offered in (Hennig, 2007) by measuring
the consistency with which a particular cluster
appears in replicated clustering - cluster-wise
stability.
The lack of a systematical relationship between
clusters validity and stability is occasionally pointed
out by diverse studies - e.g., (Cardoso et al., 2010).
Thus, a systematical study of the relationship
between stability and clustering external validity is
in order.
2.2 Cross-Validation
In order to evaluate clustering stability cross-
validation can be used. Cross-validation referred to
unsupervised analysis is described in (McIntyre and
Blashfield, 1980).
In this work we resort to the weighted cross-
validation procedure proposed in (Cardoso et al.,
2010) to evaluate the stability of clustering
solutions–see Table 1.
Table 1: Weighted cross-validation procedure.
Step Action Output
1 Perform training-test
sample split
Weighted training
and test samples
2 Cluster weighted
training sample
Clusters in the
weighted training
sample
3 Cluster weighted test
sample
Clusters in the
weighted test sample
4 Obtain a contingency
table between clusters
obtained in 2. and 3.
Indices of d
agreement values,
indicators of stability
The “weighted training sample” considers unit
weights for training observations (50% in the data
sets considered) and almost zero weights to the
remaining (test) observations. The “weighted test
sample” reverses this weights’ allocation. The use of
weighted samples overcomes the need for selecting a
classifier when performing cross-validation.
Furthermore, sample dimension is not a severe
limitation for implementing clustering stability
evaluation, since the Indices of agreement values are
based on the entire (weighted) sample, and not in a
holdout sample.
2.3 Adjusted Agreement between
Partitions
In order to measure the agreement between two
partitions we can resort to indices of agreement ().
In the literature, multiple can be found – e.g.,
(Vinh et al., 2010), (Warrens, 2008). They are
generally quantified based on the cells values of the
contingency table
between the two partitions
and
being compared with and clusters
(respectively) - and on the corresponding row totals
and column totals
.
Among the , the Rand index ( ) is,
perhaps, the most well-known - (Rand, 1971).
,
∑∑
∑
∑
(1)
It quantifies the proportion of all pairs of
observations that both partitions (
and
) agree
to join in a group or to separate into different groups.
Since agreement between partitions can occur by
chance, (Hubert and Arabie, 1985) propose an
adjusted version of using its expected value
under the hypothesis of agreement by chance (
):
∑∑
2
∑
∑
(2)
Then this is adjusted according with the general
formula:
,
,
,
,
,
(3)
The adjusted index (
is thus null when
agreement between partitions occurs by chance.
Some are based on the concepts of entropy and
information. Among these , Mutual Information
() is particularly well-known:
,
log
(4)
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
260
(Vinh et al., 2010) advocate a strategy similar to
that of Hubert and Arabie, (Hubert and Arabie,
1985), to adjust for agreement by chance. These
authors also advocate the use of a particular mutual
information form resorting to joint entropy
,
– ((Horibe, 1985), ((Kraskov et al.,
2005)):
,
,
/
,
(5)
where
,
log
(6)
In this work we use the adjusted indices
,
and
,
to investigate
agreement between two partitions. They offer
different perspectives on agreement – paired
agreement and simple agreement (Cardoso, 2007).
These views are meant to provide useful insights
when referring to external validation (comparison
between the clustering solution and the “true” cluster
structure) or to the evaluation of stability
(comparison between two clustering solutions
deriving from minor modifications in the clustering
process).
3 NUMERICAL EXPERIMENTS
The pioneer study of Milligan and Cooper, (Milligan
and Cooper, 1985), established the use of synthetic
data to support the external validation of clustering
structures. In this general setting, clustering
solutions are to be compared with a priori known
classes associated with the generated data sets. Since
then, several works referring to external validation
of clustering solutions have developed this line of
work trying to overcome some drawbacks of this
first study such as using the “right number of
clusters” to quantify external validity is limited in
scope, (Vendramin et al., 2010). Also, overlap
between clusters should be properly quantified on
the generation of experimental data sets (Steinley
and Henson, 2005).
The present research considers three main design
factors for the generation of synthetic data sets:
1. balanced (1- clusters are balanced having equal
or very similar numbers of observations; 2-
clusters are unbalanced)
2. number of clusters (K=2, 3,4)
3. clusters separation (1- poor; 2-moderate; 3- good)
The 18 resulting scenarios are named after the
previous coding – for example, the scenario with
balanced clusters (1), 3 clusters (3) and moderate
separation (2) is termed “132”.
The first design factor is operationalized as
follows: balanced settings have classes with similar
dimensions and for unbalanced settings classes have
the following a priori probabilities or weights:
a) 0.30 and 0.7 when K=2; b) 0.6, 0.3 and 0.1 when
K=3; c) 0.5, 0.25, 0.15 and 0.10 when K=4.
The increasing number of clusters is associated
with increasing number of variables (2, 3 and 4
latent groups with 2, 3 and 4 Gaussian distributed
variables) and, in order to deal with this increasing
complexity, we consider data sets with 500, 800 and
1100 observations, respectively.
The following measure of overlap between
cluster is adopted, (Maitra and Melnykov, 2010):
|
|
(7)
where
|
is the misclassification probability that
the random variable originated from the k
th
component is mistakenly assigned to the k’
th
component and
|
is defined similarly.
In order to generate the datasets within the
scenarios, we capitalize on the recent contribution in
(Maitra and Melnykov, 2010) and use the R MixSim
package to generate structured data according to the
finite Gaussian mixture model:
gx
λ
ϕx;
μ
,Σ
(8)
where
;
,Σ
is a multivariate Gaussian
density of the kth component with mean
vector
and covariance matrix Σ
. Therefore
ω
|
λ
ϕx;μ
,Σ
λ
ϕx;
,Σ
|~
μ
,Σ
(9)
Based on this measure, we consider three degrees
of overlap in the experimental scenarios: 1) ω
is
around 0.6 for poorly separated clusters; 2) ω
is
around 0.15 for moderately separated; 3) ω
is
around 0.02 for well separated classes (these
thresholds are indicated in (Maitra and Melnykov,
2010)).
For each of the referred 18 scenarios, we
generate 30 datasets and run our experiments by:
− clustering each data set;
− evaluating stability of the clustering
solution (see 2.1 and 0);
Clustering Stability and Ground Truth: Numerical Experiments
261
− evaluating clustering external validity
based on the a priori known classes (see 0);
− correlating results from stability and
external validity to assess the role of the
stability property.
The Rmixmod package is used for clustering
purposes (Lebret et al., 2012). EM algorithm is
found to be particularly suited for the clustering
tasks at hand, since the data generated follow a finite
Gaussian mixture model. We use the general
Gaussian mixture model - [P
K
L
K
C
K
] in (Biernacki et
al., 2006).
The first results obtained are summarized in
Table 2 and Table 3. They reveal the pertinence of
the design factors, the overlap measure in particular:
stability and external validity increase with the
increase in separation, the being close to zero
when separation is poor and near one when well
separated clusters are considered. In general, the
adjusted Rand index and normalized mutual
information values illustrate the same underlying
reality, although the
MIH
values provide a more
conservative view of the degree of agreement
between two partitions.
The general results referring to the relationship
between stability and agreement with ground truth
(inter experimental scenarios) are illustrated in
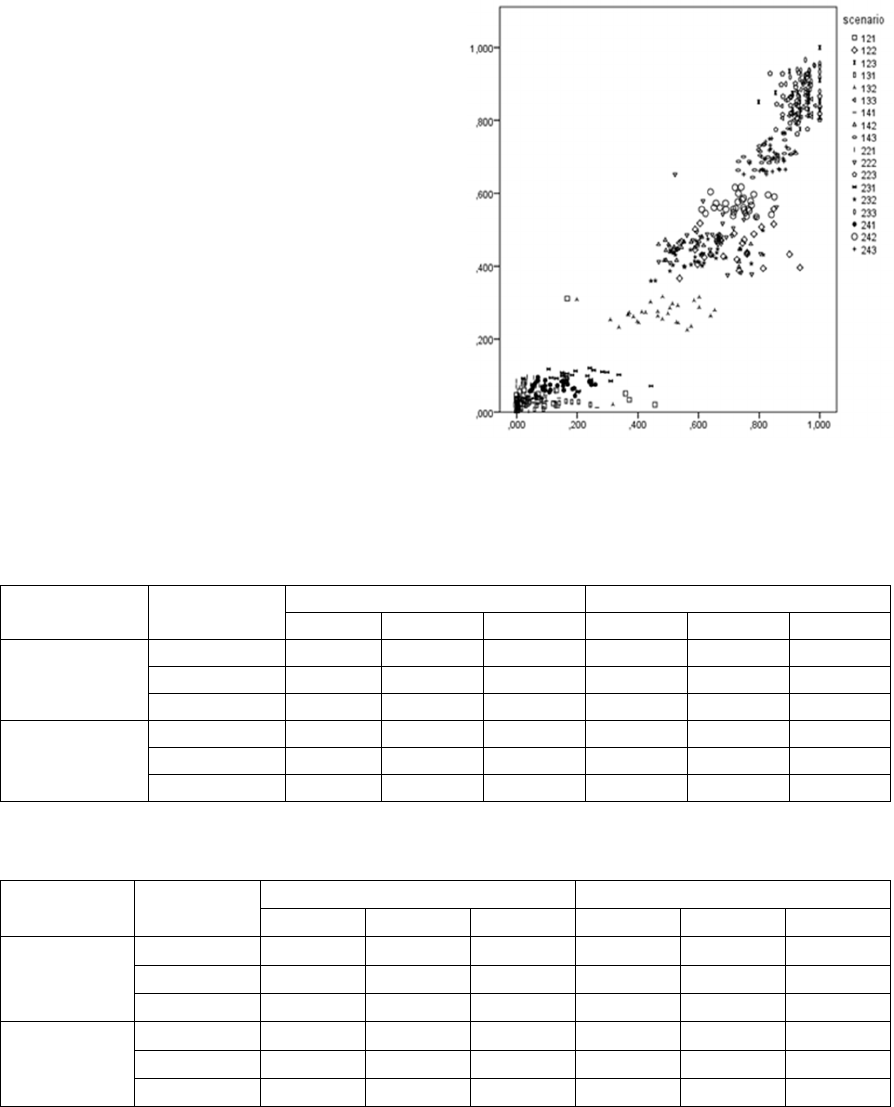
Figure 1 and Figure 2. The corresponding Pearson
correlation values are 0.958 and 0.933, respectively,
indicating a high linear correlation between stability
and external validity (both measured by
in
Figure 1 and
in Figure 2). These results
corroborate the general theory on the relevance of
the property of stability in the evaluation of
clustering solutions.
Figure 1: Inter-scenarios Pearson correlation between
stability (yy’) and agreement with ground truth (xx’): the
MIH
perspective.
Table 2: Adjusted Rand index values corresponding to external validity and to stability (values averaged over 30 datasets).
Rand
Separation
External validity Stability
K=2 K=3 K=4 K=2 K=3 K=4
Balanced
Poor 0.055 0.038 0.041 0.111 0.118 0.085
Moderate 0.728 0.388 0.624 0.865 0.652 0.688
Good 0.963 0.943 0.855 0.987 0.979 0.918
Unbalanced
Poor 0.097 0.211 0.133 0.053 0.280 0.166
Moderate 0.765 0.690 0.820 0.864 0.822 0.898
Good 0.962 0.980 0.887 0.981 0.991 0.949
Table 3: Normalized mutual information adjusted values corresponding to external validity and to stability (values averaged
over 30 datasets).
MIH
Separation
External validity Stability
K=2 K=3 K=4 K=2 K=3 K=4
Balanced
Poor 0.046 0.024 0.031 0.073 0.054 0.073
Moderate 0.458 0.263 0.449 0.700 0.465 0.578
Good 0.865 0.832 0.707 0.949 0.931 0.833
Unbalanced
Poor 0.048 0.093 0.070 0.036 0.189 0.124
Moderate 0.477 0.440 0.569 0.660 0.613 0.732
Good 0.850 0.920 0.694 0.922 0.957 0.840
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
262
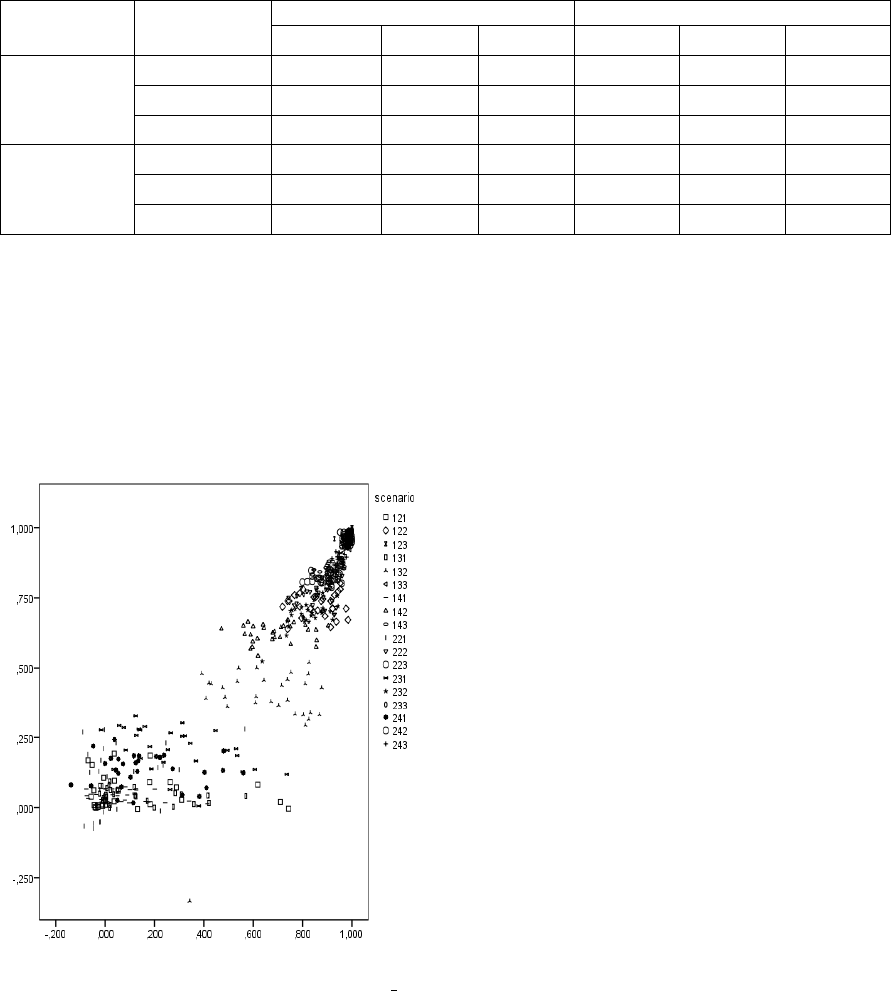
Table 4: Intra-scenarios Pearson correlations between stability and agreement with ground truth for synthetic data.
Separation
MIH
Rand
K=2 K=3 K=4 K=2 K=3 K=4
Balanced
Poor 0.143 -0.018 -0.129 -0.079 -0.155 -0.303
Moderate 0.122 0.264 -0.015 0.068 0.215 0.111
Good 0.084 0.222 0.527 0.046 0.177 0.624
Unbalanced
Poor 0.329 0.126 0.172 0.367 -0.42 -0.079
Moderate -0.003 0.593 0.084 0.085 0.666 0.084
Good -0.151 0.272 0.245 -0.084 0.159 0.218
A completely different view is however provided
intra-scenarios were very low correlations between
stability and external validity are obtained – see Table
4. Within a specific scenario - the “real deal” for any
clustering analysis practitioner - the correlation
between external validity and stability is negligible.
Both
,
and
,
lead to the
same conclusion. Only two exceptions contradict this
rule: scenarios “232” and “143”.
Figure 2: Inter-scenarios Pearson correlation between
stability (yy’) and agreement with ground truth (xx’): the
Rand
perspective.
4 CONTRIBUTIONS AND
PERSPECTIVES
In this work we analyze the pertinence of using
stability in the evaluation of a clustering solution. In
particular, we question the following: does the
consistency of a clustering solution (resisting minor
modifications of the clustering process) provide
indication towards a greater agreement with the
“ground truth” (true structure) of the data?
In order to address this issue, we design an
experiment in which 540 synthetic data sets are
generated under 18 different scenarios. Design factors
considered are the number of clusters, their balance
and overlap. In addition, different sample sizes and
space dimensions are considered.
Through the use of weighted cross-validation, we
enable the analysis of stability, (Cardoso et al., 2010).
We resort to adjusted indices of agreement (excluding
agreement by chance) to measure agreement between
two clustering solutions and also between a clustering
solution and the “true” classes: we specifically use a
simple index of agreement - the adjusted normalized
Mutual Information, (Vinh et al., 2010) - and a paired
one - the adjusted Rand índex (Hubert and Arabie,
1985).
A macro-view of the results does not contradict
the current theory - there is a strong correlation
between stability and external validity when the
aggregate results are considered (all scenarios’
results).
However, when it comes to perform clustering
analysis within a specific experimental scenario, what
can we say about the same correlation? The
conclusions derived in this case support the
previously referred concerns – there is an
insignificant correlation between stability and
external validity when it comes to a specific
clustering problem.
Of course, it is still true that an unstable solution
is, for this very reason, undesirable: then, which
results should the practitioner consider? However, in
a specific clustering setting, there is clearly no
credible link between the stability of a partition and
its approximation to ground truth.
This work contributes with a new perspective for
a better understanding of the relationship between
clustering stability and its external validity. To our
Clustering Stability and Ground Truth: Numerical Experiments
263
knowledge, is the first time a study distinguishes
between the macro view (all experimental scenarios
considered) and the micro view (considering a
specific clustering problem) and clearly differentiates
the corresponding results.
In the future, stability results in discrete clustering
should also be assessed and possible additional
experimental factors also considered (e.g., the
clusters’ entropy).
In the future, clustering stability results in real
data sets should also be assessed.
REFERENCES
Ben-David, S. & Luxburg, U. V., 2008. Relating clustering
stability to properties of cluster boundaries. In:
Servedio, R. & Zhang, T., eds. 21st Annual Conference
on Learning Theory (COLT), Berlin. Springer, 379-390.
Biernacki, C., Celeux, G., Govaert, G. & Langrognet, F.,
2006. Model-Based Cluster and Discriminant Analysis
with the MIXMOD Software. Computational Statistics
and Data Analysis, 51, 587-600.
Bubeck, S., Meila, M. & Von luxburg, U., 2012. How the
initialization affects the stability of the k-means
algorithm. ESAIM: Probability and Statistics, 16, 436-
452.
Cardoso, M. G., Faceli, K. & De Carvalho, A. C., 2010.
Evaluation of Clustering Results: The Trade-off Bias-
Variability. Classification as a Tool for Research.
Springer, 201-208.
Cardoso, M. G. M. S., 2007. Clustering and Cross-
Validation. In: C. Ferreira, C. L., G. Saporta And M.
Souto De Miranda, ed. IASC 07 - Statistics for Data
Mining, Learning and Knowledge Extraction, Aveiro,
Portugal.
Celeux, G. & Diebolt, J., 1985. The SEM Algorithm: A
probabilistic teacher algorithm derived from the EM
algorithm for the mixture problem. Computational
Statistics Quarterly, 2, 73-82.
Chiang, M. M.-T. & MIrkin, B., 2010. Intelligent Choice of
the Number of Clusters in K-Means Clustering: An
Experimental Study with Different Cluster Spreads.
Journal of Classification, 27, 3-40.
Dempster, A. P., Laird, N. M. & Rubin, D. B., 1977.
Maximum likelihood from incomplete data via the EM
algorithm. Journal of the Royal Statistics Society. Series
B (Methodological), 39, 1-38.
Hartigan, J. A., 1975. Clustering algorithms.
Hennig, C., 2007. Cluster-wise assessment of cluster
stability. Computational Statistics & Data Analysis, 52,
258-271.
Horibe, Y., 1985. Entropy and correlation. Systems, Man
and Cybernetics, IEEE Transactions on, 5, 641-642.
Hubert, L. & Arabie, P., 1985. Comparing partitions.
Journal of Classification, 2, 193-218.
Jain, A. K. & Dubes, R. C., 1988. Algorithms for clustering
data, Englewood Cliffs, N.J.: Prentice Hall.
Kraskov, A., Stögbauer, H., Andrzejak, R. G. &
Grassberger, P., 2005. Hierarchical clustering using
mutual information. EPL (Europhysics Letters), 70,
278.
Lange, T., Roth, V., Braun, M. L. & Buchman, J. M., 2004.
Stability based validation of clustering solutions.
Neural Computation, 16, 1299-1323.
Lebret, R., S., L., Langrognet, F., Biernacki, C., Celeux, G.
& Govaert, G., 2012. Rmixmod: The r package of the
model-based unsupervised, supervised and semi-
supervised classification [Online]. Rmixmod library.
http://cran.rproject.org/web/packages/Rmixmod/index.
html
Luxburg, U. V., 2009. Clustering Stability: An Overview.
Machine Learning, 2, 235-274.
Maitra, R. & Melnykov, V., 2010. Simulating data to study
performance of finite mixture modeling and clustering
algorithms. Journal of Computational and Graphical
Statistics, 19, 354-376.
Mcintyre, R. M. & Blashfield, R. K., 1980. A nearest-
centroid technique for evaluating the minimum-
variance clustering procedure. Multivariate Behavioral
Research, 2, 225-238.
Milligan, G. W. & Cooper, M. C. 1985. An examination of
procedures for determining the number of clusters in a
data set. Psychometrika, 50, 159-179.
Rand, W. M., 1971. Objective criteria for the evaluation of
clustering methods. Journal of the American Statistical
Association, 66, 846-850.
Steinley, D. & Henson, R., 2005. OCLUS: an analytic
method for generating clusters with known overlap.
Journal of Classification, 22, 221-250.
Vendramin, L., Campello, R. J. & Hruschka, E. R., 2010.
Relative clustering validity criteria: A comparative
overview. Statistical Analysis and Data Mining, 3, 209-
235.
Vinh, N. X., Epps, J. & Bailey, J., 2010. Information
theoretic measures for clusterings comparison:
Variants, properties, normalization and correction for
chance. The Journal of Machine Learning Research,
11, 2837-2854.
Warrens, M. J., 2008. On similarity coefficients for 2× 2
tables and correction for chance. Psychometrika, 73,
487-502.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
264
