Gaussian Nonlinear Line Attractor for Learning Multidimensional Data
Theus H. Aspiras
1
, Vijayan K. Asari
1
and Wesam Sakla
2
1
Department of Electrical and Computer Engineering, University of Dayton, U.S.A.
2
Air Force Research Laboratory, Wright Patterson Air Force Base, U.S.A.
Keywords:
Nonlinear Line Attractor, Multidimensional Data, Neural Networks, Machine Learning.
Abstract:
The human brain’s ability to extract information from multidimensional data modeled by the Nonlinear Line
Attractor (NLA), where nodes are connected by polynomial weight sets. Neuron connections in this archi-
tecture assumes complete connectivity with all other neurons, thus creating a huge web of connections. We
envision that each neuron should be connected to a group of surrounding neurons with weighted connection
strengths that reduces with proximity to the neuron. To develop the weighted NLA architecture, we use a
Gaussian weighting strategy to model the proximity, which will also reduce the computation times signifi-
cantly. Once all data has been trained in the NLA network, the weight set can be reduced using a locality
preserving nonlinear dimensionality reduction technique. By reducing the weight sets using this technique,
we can reduce the amount of outputs for recognition tasks. An appropriate distance measure can then be used
for comparing testing data and the trained data when processed through the NLA architecture. It is observed
that the proposed GNLA algorithm reduces training time significantly and is able to provide even better recog-
nition using fewer dimensions than the original NLA algorithm. We have tested this algorithm and showed
that it works well in different datasets, including the EO Synthetic Vehicle database and the Sheffield face
database.
1 INTRODUCTION
Much research work has been done on modeling brain
functions and activities. The brain has around 10
11
neurons and each neuron has up to ten thousand
synaptic connections to other neurons around it. The
brain has a unique ability to utilize groups of these
neurons to formulate different lobes and structures to
regulate bodily functions, emotional responses, and
even cognition. All of these structures are able to
unify together to handle numerous inputs from the
different senses and have the ability to respond simul-
taneously.
When developing neurons and synaptic weights
of the brain, models for these must have a set struc-
ture, an ability for firing/nonfiring of neurons through
the synaptic junctions, training of the structure, and
continuous training of the system. Artificial neural
networks are the most explored models of the hu-
man brain, which encompass different modeling tech-
niques of the brain. One area of neural networks is
the recurrent neural network, which are able to send
outputs to the same stage of the network. This type
of neural network is also called an attractor network,
which attracts towards a certain pattern. In this paper,
we will be exploring attractor networks and how to
improve them.
1.1 Attractor Neural Networks
There are different types of attractor networks which
can model different dynamics of networks. One type
is the fixed point attractor, which is the Hopfield net-
work (Hopfield, 1982). Given an underlying energy
function for minimization, the network asymptoti-
cally approaches a desired state. These networks are
associative, meaning that they can approach towards a
specific state given only part of the data. Other types
include the cyclic attractor networks to govern oscil-
latory behaviors (Lewis and Glass, 1991). The type
we will be focusing on is the line attractor (Zhang,
1996).
Line attractor networks work well for states that
are not just a specific point but a line of points. Point
attractor networks disregard any ability to attract to
a specific trained image of a class, unless there are
multiple point attractors for one class. Line attrac-
tor network assume continuity between data points,
which allows an estimation of data points that are
not fully trained in the dataset. Since manifolds in
130
Aspiras, T., Asari, V. and Sakla, W..
Gaussian Nonlinear Line Attractor for Learning Multidimensional Data.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 3: NCTA, pages 130-137
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
a high-dimensional space are usually nonlinear, it is
best to incorporate a nonlinear line attractor to model
the manifold in space. Thus in this paper, we utilize
the nonlinear line attractor (NLA) network as the sup-
porting architecture for our work.
1.2 Biological Implications
With the use of recurrent associative networks, most
are totally interconnected, meaning that every node is
connected to all other nodes. This type of architec-
ture allows influence of all nodes, especially if there
are significant changes in input at farther nodes. But
in biological structures, nodes are only interconnected
with surrounding nodes with longer, weaker connec-
tions with farther nodes. These types are expressed
by Tononi et al. (Tononi et al., 1999), who found that
there is much redundancy in highly interconnected
networks. They introduced an optimized degenera-
tive case, which minimizes the amount of connections
while maintaining the cognitive ability and reducing
redundancy.
By using only neighborhood connections, por-
tions of the network will be responsible for model-
ing that region while relying on the propagation of
influence from other sections to travel as the network
iterates. This local modeling will aid in faster conver-
gence due to reliance to only closer nodes and give
way to higher variance areas, which contain more in-
formation than other areas of input, for example a
background region. This also reduces the amount of
redundancies in the network for modeling a specific
portion of data. Guido et al. (Guido et al., 1990)
found that there is functional compensation when the
visual cortex, which is highly modular, is damaged.
1.3 Modularity in Neural Networks
By developing neighboring connections, we can cre-
ate modularity while still keeping inter-connectivity
in the networks. Happel et al. (Happel and Murre,
1994) investigated various interconnections and mod-
ularity in networks and found that different configu-
rations aided in further recognition of different tasks.
Other techniques also used modularity, like modu-
lar principal component analysis (Gottumukkal and
Asari, 2004), which takes specific portions of an im-
age and takes the PCA of those sub-images to aid in
the recognition of the whole image. Modularity re-
duces the model complexity which uses specific mod-
ules to learn only a portion of data to aid in the overall
complex task (Gomi and Kawato, 1993).
Instead of fully incorporating modularity, algo-
rithms also include overlap between modules to im-
prove the recognition capabilities. Auda et al. (Auda
and Kamel, 1997) used Cooperative Modular Neural
Networks with various degrees of overlap to improve
various classification applications. Also since mod-
ularity reduces the amount of connections between
neurons by dividing processing into smaller subtasks,
the amount of computations can be greatly reduced.
The type of neural network we will be looking at
is the nonlinear line attractor, proposed by Seow et
al. (Seow and Asari, 2004), which has been used for
skin color association, pattern association (Seow and
Asari, 2006), and pose and expression invariant face
recognition (Seow et al., 2012). Given that modu-
larity is able to reduce computation complexity and
improve recognition in many cases, we aim to incor-
porate it into the nonlinear line attractor network. In-
stead of complete modularity, we propose a smooth,
Gaussian weighting strategy to make smooth overlaps
for each module. According to the weighting scheme
of the network, modularity will also reduce the com-
plexity of the modeling of the network. In (Seow
et al., 2012), the weighting scheme is reduced using
Nonlinear Dimensionality Reduction. We will look
into the ability of the algorithm to reduce the weights
and propose an improvement to the algorithm.
The main contributions of this paper are:
• Gaussian weighting strategy to the Nonlinear Line
Attractor Network to introduce modularity
• Reduction of the computational complexity to im-
prove the convergence time of the GNLA archi-
tecture
• An improved scenario for using the Nonlinear Di-
mensionality Reduction for object recognition
2 METHODOLOGY
The nonlinear line attractor network is a recurrent as-
sociative neural network, which aims to converge on
a trained pattern given an input. Each trained pat-
tern has connective information, which links one de-
gree of information to another. These trained patterns
usually are learned as a point in the feature space
and thus variations of the pattern would be repre-
sented as a basin. Convergence would specify that
the input pattern would be associated to one of the
learned patterns. When considering a basin of attrac-
tion, single point representations of a particular set
of patterns may be insufficient to totally encompass
the patterns. The NLA architecture formulates a non-
linear line representation which would allow patterns
to converge towards the line attractor. An example
would be using manifold learning on a set of objects
Gaussian Nonlinear Line Attractor for Learning Multidimensional Data
131

with varying poses. As the poses move in the high-
dimensional space, the manifold would form a non-
linear line, which would be best modeled by the NLA
architecture.
Let the response x
i
of the i
th
neuron due to the
excitations x
j
from other neurons for the s
th
pattern
in a fully connected recurrent neural network with n
neurons be expressed as:
x
(i,s)
=
1
N
N
∑
j=1
Λ
i
(x
( j,s)
) for 1 ≤ i ≤ N (1)
where Λ
i
is defined by a k
th
order nonlinear line
as:
Λ
i
(x
( j,s)
) =
k
∑
m=0
w
(m,i j)
(x
( j,s)
)
m
for 1 ≤ i, j ≤ N (2)
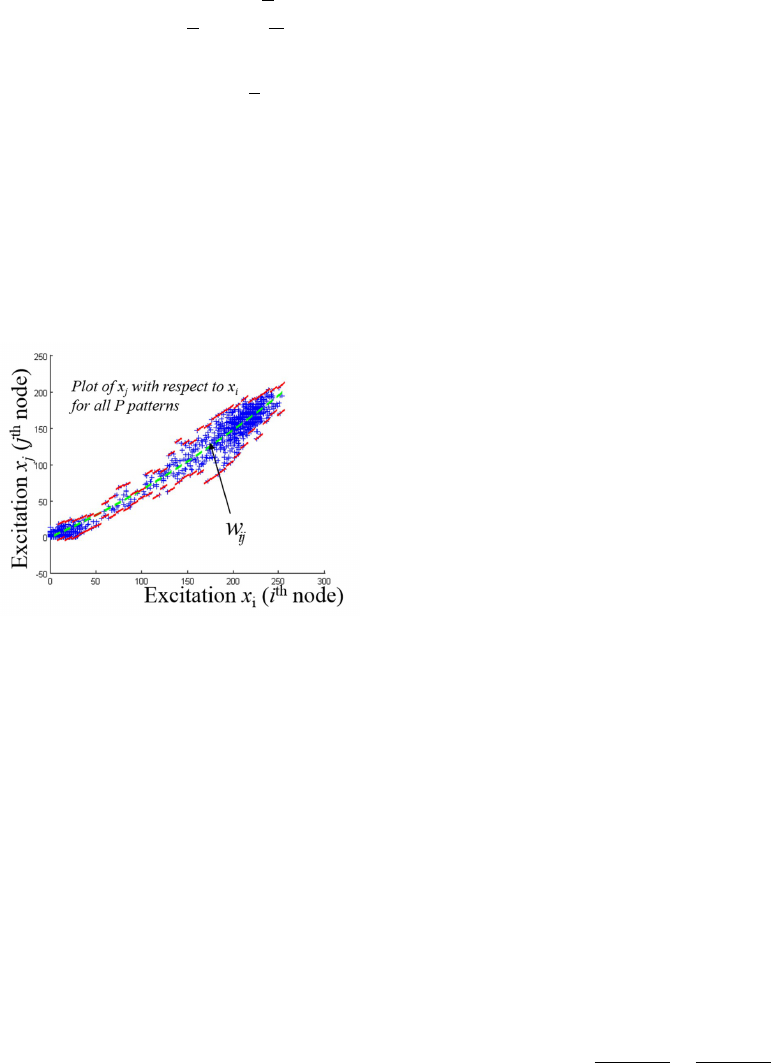
This equation defines a polynomial best fit line to
encompass all input/output pairs given from each pat-
tern s. The green line in Figure 1 shows this best fit
line. The m
th
order term of the resultant memory w
m
can be expressed as:
w
m
=
w
(m,11)
. . . w
(m,1N)
.
.
.
.
.
.
.
.
.
w
(m,N1)
. . . w
(m,NN)
for 0 ≤ m ≤ k
(3)
The weights are in matrix form to show a fully
interconnected weight system. Since the input and
output have the same number of nodes due to the as-
sociative nature of the algorithm, we can show these
weights in this regard. To calculate the weights, we
can use error descending characteristics. The least
squares estimation approach is able to calculate the
best fit line using the polynomial method. To mini-
mize the least squares error in the weight matrix, we
can formulate the following equation, which yields
the optimum weight set.
E
i j
[w
(0,i j)
,w
(1,i j)
, ..., w
(k,i j)
] =
P
∑
s=1
[x
(i,s)
− Λ
i
(x
( j,s)
)]
2
for 1 ≤ s ≤ P
(4)
To minimize the least squares error, we must
equate the derivative of the error with respect to the
weight to be zero, as shown in the following equation.
δE
i j
δw
(m,i j)
= 0 for each m = 0, 1, . . . , k (5)
We can then find that the equation can be reduced
to a set of linear equations based on the order of the
polynomial, as shown below.
w
(0,i j)
P
∑
s=1
(x
( j,s)
)
0
+ w
(1,i j)
P
∑
s=1
(x
( j,s)
)
1
+ . . .
+ w
(k,i j)
P
∑
s=1
(x
( j,s)
)
k
=
P
∑
s=1
x
(i,s)
(x
( j,s)
)
0
w
(0,i j)
P
∑
s=1
(x
( j,s)
)
1
+ w
(1,i j)
P
∑
s=1
(x
( j,s)
)
2
+ . . .
+ w
(k,i j)
P
∑
s=1
(x
( j,s)
)
k+1
=
P
∑
s=1
x
(i,s)
(x
( j,s)
)
1
.
.
.
w
(0,i j)
P
∑
s=1
(x
( j,s)
)
k
+ w
(1,i j)
P
∑
s=1
(x
( j,s)
)
k+1
+ . . .
+ w
(k,i j)
P
∑
s=1
(x
( j,s)
)
2k
=
P
∑
s=1
x
(i,s)
(x
( j,s)
)
k
(6)
Given that there is a nonlinear line that models
the relationship between inputs, as modeled by the
trained weight sets, there must be another modeling
of the variances of the data. This is done by creating
an activation function, as shown in equation 7.
Φ
Λ[x
j
(t + 1)]
=
x
i
(t) if ψ
(i j,−)
≤ {Λ
i
[x
j
(t + 1) − x
i
(t + 1)}
≤ ψ
(i j,+)
Λ
i
[x
j
(t + 1)] otherwise
(7)
where
Λ
i
(x
j
(t)) =
k
∑
m=0
w
(m,i j)
(x
j
(t))
m
(8)
An activation function can be used to see if a data
point that runs through the system is trained into the
manifold. Since data points do not exactly fit in the
best fit nonlinear line, thresholds [ψ
(i j,−)
, ψ
(i j,+)
] are
created to ensure that data points do not update if
the estimated data point lies within the manifold. If
the data point falls away from the manifold, the best
fit equation can be used to attract the data point to-
wards the manifold. These threshold regions can be
expressed as:
ψ
(i j,−)
=
ψ
(1,i j,−)
if 0 ≤ x
j
<
L
Ω
ψ
(2,i j,−)
if
L
Ω
≤ x
j
<
2L
Ω
.
.
.
ψ
(Ω,i j,−)
if (Ω − 1)
L
Ω
≤ x
j
< L
(9)
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
132
ψ
(i j,+)
=
ψ
(1,i j,+)
if 0 ≤ x
j
<
L
Ω
ψ
(2,i j,+)
if
L
Ω
≤ x
j
<
2L
Ω
.
.
.
ψ
(Ω,i j,+)
if (Ω − 1)
L
Ω
≤ x
j
< L
(10)
where L is the number of segments used for the
piecewise threshold regions and Ω is the length of the
manifold. When using a nonlinear dimensionality re-
duction technique, as shown in a further section, the
threshold regions created will not be used, due to the
nonlinear line attractor becoming a transform from
the original image space to a reduced dimensionality
space. Figure 1 shows how the weights are intercon-
nect through the inputs.
Figure 1: Interconnection of Weights. The green line cap-
tures the nonlinear line modeling and the red lines capture
the variances of the data.
Since this is modeling of a specific manifold, mul-
tiple manifolds may be needed to encompass more
of a class. Most will require a specific manifold per
class, so there will be at least one weight set per class.
2.0.1 Computational Strategy
We have devised an effective computational strategy
for training data. Given equation 6, previous mod-
els of the computational strategy require computing
powers for each interconnection, in which there are
several calculations that are repeated in the equations
while traversing through each interconnection. In-
stead of having redundant calculations, we can divide
the weight calculation into different steps.
Stage 1 would be the calculation of powers for the
inputs. In equation 6, we see that every x
s
j
has an order
associated with it. Calculation of these terms would
be redundant for all different combinations of inputs
and outputs, since there are multiple terms with the
same order, hence the same value. Computing only
the powers in this stage would tremendously reduce
the computation time of the system.
Stage 2 would be the calculation of the weights,
given the set of normal equations and using the val-
ues obtained from stage 1. The solving of the nor-
mal equations can be done using a linear solve al-
gorithm. This stage will take a considerable amount
of time due to the volume of data, specifically the
number of inputs, since the weight matrix size is
#inputs × #inputs × order where # inputs refer to the
size of the image.
Stage 3 would be the calculation of the activa-
tion function, which will also require a considerable
amount of computation time. Since the computa-
tion of the orders for all of the input data are already
known, the activation function can be formulated us-
ing that data.
Stage 4 would be the calculation of the nonlinear
dimensionality reduction. This step would require all
of the weights and is dependent on the number of in-
puts and also the order of the weight system.
2.1 Gaussian Nonlinear Line Attractor
(GNLA) Network
The Gaussian Nonlinear Line Attractor Network is a
modification to the original NLA network, which uses
a neighborhood approach to improve the algorithm.
Local information is more important than distant in-
formation, when looking from a biological perspec-
tive, so it can be assumed that using this architecture
for the NLA algorithm would improve run times and
classification ability. When dealing with imagery, a 2-
dimensional spatial relationship is created with each
node. By incorporating this spatial relationship into
the nodes, we can increase the recognition while re-
ducing computation time.
When implementing a Gaussian neighborhood ap-
proach, we can change the coefficient in the front and
add the distance equation. The equation can then be
modified as:
x
(i,s)
=
N
∑
j=1
α
i j
Λ
i
(x
( j,s)
) for 1 ≤ i ≤ N (11)
where
α
i j
= exp
−
( ˆx
i
− ˆx
j
)
2
2σ
2
ˆx
+
( ˆy
i
− ˆy
j
)
2
2σ
2
ˆy
!!
(12)
For these equations, ˆx and ˆy define the spatial co-
ordinates of the input x. Instead of using the Gaus-
sian function, we can use the Gaussian kernel , for
example a 13x13 Gaussian kernel as shown in Figure
2. This will effectively reduce the computation time.
We can then change the equation as
Gaussian Nonlinear Line Attractor for Learning Multidimensional Data
133

Figure 2: An example of a 13 x 13 Gaussian kernel.
x
(i,s)
=
N
∑
j=1
A
i j
Λ
i
(x
( j,s)
) for 1 ≤ i ≤ N (13)
Where n is the size of the kernel and A
i j
A
i j
= exp
−
( ˆx
i
− ˆx
j
)
2
2σ
2
ˆx
+
( ˆy
i
− ˆy
j
)
2
2σ
2
ˆy
!!
(14)
We can also effectively reduce the computation
time of the kernel by not computing any portion that
contains zeros. According to the Gaussian kernel
above (which is a 13x13), roughly 28% of the Gaus-
sian kernel are zeros, thus a reduction of the computa-
tion time can be accomplished by ignoring those com-
putations.
2.1.1 Nonlinear Dimensionality Reduction
To reduce the size of the weight sets, we can reduce
the dimensionality of the weights. Since the weights
obtained through training have embedded the mani-
folds, we can use the weights in the reduction process.
Given that there are r different line attractor networks,
there will be y different outputs, as shown in the fol-
lowing equation.
Y
1
= W
1,k
X
k
+W
1,k−1
X
k−1
+ ··· +W
1,0
X
0
Y
2
= W
2,k
X
k
+W
2,k−1
X
k−1
+ ··· +W
2,0
X
0
.
.
.
Y
r
= W
r,k
X
k
+W
r,k−1
X
k−1
+ ··· +W
r,0
X
0
(15)
Previous algorithms of the Nonlinear Line Attrac-
tor use singular value decomposition (SVD) (Golub
and Reinsch, 1970) to reduce the weight set. We pro-
pose using a different strategy to reduce the weight
set. Given that the locally linear embedding (LLE)
(Roweis and Saul, 2000) algorithm contains intercon-
nected weight sets for different datapoints, we can use
that strategy to reduce the weights of the NLA net-
work.
Each m
th
term of the networks’ memory is evalu-
ated using the LLE algorithm. We first obtain a sparse
matrix M using the following equation.
M
(m,d)
=(I − w
(m,d)
)
0
∗ (I − w
(m,d)
)
for 0 ≤ m ≤ k; 1 ≤ d ≤ r
(16)
We then take the smallest z eigenvectors from
M and use them as the projection into the lower-
dimensional subspace. The projection of the N-
dimensional data to a z-dimensional subspace using a
z × N sub-matrix obtained from the smallest z eigen-
vectors of the LLE yields a z-dimensional output Y
0
m
where z << N. Once the lower-dimensional subspace
is obtained, we can then use an appropriate distance
measure, like Euclidean distance, to find the closest
match of a test image to the trained images in the sys-
tem.
When calculating the weight matrices for the
Gaussian NLA network, none of the weights contain
any information of the Gaussian distances. To incor-
porate the function inside the weights, we must embed
the terms into the weights by multiplying the normal-
ized mask with the weights. Given equation 16, we
can embed the normalized coefficients to multiply the
weights using the following equation.
a
s
=
a
s
(11)
. . . a
s
(1N)
.
.
.
.
.
.
.
.
.
a
s
(N1)
. . . a
s
(NN)
(17)
The resultant multiplication of the weight set is
given by the equation below.
¯w
(m,s)
=
¯w
(m,11,s)
. . . ¯w
(m,1N,s)
.
.
.
.
.
.
.
.
.
¯w
(m,N1,s)
. . . ¯w
(m,NN,s)
for 0 ≤ m ≤ k
(18)
This nonlinear dimensionality reduction tech-
nique using LLE computes each order of the weight
matrices separately. There is no interconnection be-
tween the orders, in which the original algorithm con-
tains a summation between the orders to results in the
final outputs. We propose that instead of reducing this
dimensionality by adding the orders of the matrix for
the results, we can concatenate all of the orders, which
are multiplied by the input, to yield a larger vector
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
134
without the reduction resulting from the summation.
This will allow even better recognition results using
fewer total weights, even though the resulting vector
can be potentially larger.
2.1.2 Complexity
In Stage 1, we can find that it will be the same com-
plexity as the previous algorithm since we are just
computing the powers.
In Stage 2, the original complexity is #inputs ×
#inputs × order
2
due to the linear solve algorithm,
but modified complexity is #inputs × #neighbors ×
order
2
, where # neighbors is significantly smaller
than the size of the network. For example, given that
we have a network of 60x80, which is 4800, and an
order of 4 for the polynomial, the complexity of the
algorithm becomes 4800 × 4800 × 4
2
= 368640000
computations. If we create kernel of size 13 × 13,
we would have a complexity of 4800 × 169 × 4
2
=
12979200 computations, which is 3.52% the compu-
tation time of the original. If we reduce the kernel by
taking out all zeros in the function, we would have
a complexity of 4800 × 121 × 4
2
= 9292800 compu-
tation, which is only 2.52% the computation time of
the original and 71.6% the computation time of the
kernel.
In Stage 3, the complexity should be reduced just
as stage 2. In Stage 4, the complexity should be the
same as the previous algorithm. Table 1 shows the run
times on the EO Synthetic Vehicle dataset. It is found
that the kernel algorithm without using zeros provides
faster training times than all of the other algorithms.
3 RESULTS
3.1 Datasets
Various datasets are being used to test the validity of
using the Nonlinear Line Attractor network for us-
age in classification and modeling tasks. One dataset
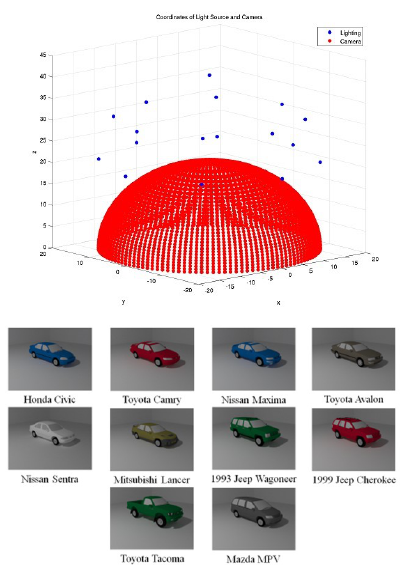
is a EO Synthetic Vehicle Database, which contains
several different cars, various lighting conditions, and
multiple viewing angles, as shown in Figure 3. This
dataset tests the algorithms ability to model an en-
tire vehicle manifold across these different scenarios.
The other dataset is the Sheffield (previously UMIST)
database, which contains several images of faces with
varying poses. For all datasets, a 13x13 kernel is used
for training and testing the dataset.
Figure 3: EO Synthetic Vehicle Database. The top image
shows the different camera and lighting positions of the
database and the images below show the different vehicles.
3.2 Results 1
The first dataset is the EO Synthetic Vehicle database.
The results are shown in Table 2. We used a full 360
view of each vehicle and one lighting condition to
train and test the validity of the technique. Weight ma-
trices were trained with all views and tested accord-
ing to the closest distance between each point (Eu-
clidean distance). It is observed that by concatenating
all of the results from the nonlinear dimensionality
reduction, we are able to keep some of the distinc-
tion found in the orders rather than summing them.
When we start adding more principal components ob-
tained from the the method, we are able to increase
the recognition result. It is observed that the GNLA
architecture and concatenating the orders is able to
decrease the number of principal components while
keeping the recognition result of the vehicles high.
3.3 Results 2
The second dataset we use is the Sheffield database.
The results are shown in Table 3. We split the whole
database into two for testing and training sets. Once
we have trained the network with the training set,
we then perform nonlinear dimensionality reduction
Gaussian Nonlinear Line Attractor for Learning Multidimensional Data
135

Table 1: Training times for each stage of the algorithms.
Runtime Original Current Kernel Kernel (No zeros)
Stage 1 N/A 15.2 min 15.2 min 15.2 min
Stage 2 1280 min 95.3 min 3.35 min 2.4 min
Stage 3 87.5 min 87.5 min 3.08 min 2.21 min
Stage 4 10.8 min 10.8 min 10.8 min 10.8 min
Total Runtime 1378.3 min 208.8 min 32.43 min 30.61 min
Table 2: Recognition results on the EO Synthetic Vehicle Database.
# Prin. Comp. NLA Reg. NLA Concat. GNLA Reg. GNLA Concat.
1 47.50 60.56 35.83 43.89
2 59.72 66.94 82.78 76.94
3 86.67 79.72 63.06 85.28
4 61.39 85.00 76.94 88.61
5 63.89 86.11 81.67 88.89
6 69.17 88.06 85.00 91.11
7 66.94 87.50 86.39 91.39
8 75.28 88.89 87.22 92.22
9 72.22 86.39 91.39 95.00
10 78.61 87.22 91.94 94.72
All 99.19 85.28 99.44 99.17
Table 3: Recognition results on the Sheffield Database.
Algorithm % Recognition
PCA 86.87
KPCA 87.64
LDA 90.87
DPCA 92.90
DCV 91.51
B2DPCA 93.38
GNLA 93.33
GNLA (concat) 94.07
and then found the closest match using Euclidean
distance. We have found that the GNLA architec-
ture works well to recognize the different faces. It
is observed that the GNLA network with concatenat-
ing the orders produced the best results. One of the
major components about the GNLA architecture is
that it runs much faster than the previous architecture.
Run time for one instance of the NLA architecture for
this dataset takes 8.2 hours, while an instance of the
GNLA architecture will take 0.8 hours.
3.4 Discussion
The biggest concern when using associative networks
is that these algorithms work best using orthogonal
data. Given a large dataset that has only small vari-
ances between different classes while having large
variances within the classes, the data is much harder
to classify with the network. Ideally, the network
should have all orthogonal inputs so that modeling
and classification of the data are much easier.
With the GNLA architecture, we are able to in-
crease orthogonality by reducing the number of inputs
sent to a given neuron. This is done by only using a
given area for computation of the algorithm. If the
input image is not any of the trained images, we will
see that the image will diverge in the portions of the
data that have the highest variance. Portions of the
image that contain background information will not
be able to converge or diverge since those sections do
not vary.
More importantly, depending on the relationship
created by the NLA architecture for the node connec-
tions, some relationships have a stronger discerning
ability than others, meaning that the nonlinear line
that has been created to model the relationship of the
nodes should have the smallest error (smallest devi-
ation from the created line). For example, if the im-
age wants to converge to one of the trained images,
we must allow those portions with stronger discern-
ing ability to function more than those portions that
are unable to converge or diverge from the input.
Since the NLA architecture allows a summation of
the relationships of the different nodes to estimate one
specific node, we must allow the portions that have
more discerning ability to be forefront in the weight-
ing scheme. This is why the Gaussian NLA architec-
ture is able to reduce the run times of the algorithm
and increase the convergence rate. Sections of the
object region are assumed to have high amounts of
variability for the relationship created by the NLA in
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
136
that specific area to all have high discerning ability,
thus allowing better convergence of trained images
and better divergence characteristics for untrained im-
ages.
4 CONCLUSIONS
The proposed GNLA architecture using the concate-
nation of the orders and the locality preserving algo-
rithm works well for recognition tasks and for reduc-
ing the amount of computation time. Previous archi-
tectures are much slower and have decent recognition
results, but by incorporating spatial information in the
weighting of the architecture, we are able to increase
the recognition results for a smaller number of dimen-
sions while reducing the computation time. We plan
to improve the weighting performance by exploring
different weighting schemes to weight those portions
of the network that are able to produce significant re-
sults.
REFERENCES
Auda, G. and Kamel, M. (1997). Cmnn: cooperative mod-
ular neural networks for pattern recognition. Pattern
Recognition Letters, 18(11):1391–1398.
Golub, G. H. and Reinsch, C. (1970). Singular value de-
composition and least squares solutions. Numerische
Mathematik, 14(5):403–420.
Gomi, H. and Kawato, M. (1993). Recognition of manip-
ulated objects by motor learning with modular archi-
tecture networks. Neural Networks, 6(4):485–497.
Gottumukkal, R. and Asari, V. K. (2004). An improved
face recognition technique based on modular pca ap-
proach. Pattern Recognition Letters, 25(4):429–436.
Guido, W., Spear, P., and Tong, L. (1990). Functional com-
pensation in the lateral suprasylvian visual area fol-
lowing bilateral visual cortex damage in kittens. Ex-
perimental brain research, 83(1):219–224.
Happel, B. L. and Murre, J. M. (1994). Design and evolu-
tion of modular neural network architectures. Neural
networks, 7(6):985–1004.
Hopfield, J. J. (1982). Neural networks and physical sys-
tems with emergent collective computational abili-
ties. Proceedings of the national academy of sciences,
79(8):2554–2558.
Lewis, J. E. and Glass, L. (1991). Steady states, limit
cycles, and chaos in models of complex biological
networks. International Journal of Bifurcation and
Chaos, 1(02):477–483.
Roweis, S. T. and Saul, L. K. (2000). Nonlinear dimension-
ality reduction by locally linear embedding. Science,
290(5500):2323–2326.
Seow, M.-J., Alex, A. T., and Asari, V. K. (2012). Learning
embedded lines of attraction by self organization for
pose and expression invariant face recognition. Opti-
cal Engineering, 51(10):107201–1.
Seow, M.-J. and Asari, V. K. (2004). Recurrent network
as a nonlinear line attractor for skin color association.
In Advances in Neural Networks–ISNN 2004, pages
870–875. Springer.
Seow, M.-J. and Asari, V. K. (2006). Recurrent neural net-
work as a linear attractor for pattern association. Neu-
ral Networks, IEEE Transactions on, 17(1):246–250.
Tononi, G., Sporns, O., and Edelman, G. M. (1999). Mea-
sures of degeneracy and redundancy in biological net-
works. Proceedings of the National Academy of Sci-
ences, 96(6):3257–3262.
Zhang, K. (1996). Representation of spatial orientation
by the intrinsic dynamics of the head-direction cell
ensemble: a theory. The journal of neuroscience,
16(6):2112–2126.
Gaussian Nonlinear Line Attractor for Learning Multidimensional Data
137
