For Sale or Wanted: Directed Crossover in Adjudicated Space

Jeannie M. Fitzgerald and Conor Ryan

Biocomputing and Developmental Systems Group, University of Limerick, Limerick, Ireland

Keywords:

Search Spaces, Directed Crossover, Genetic Programming.

Abstract:

Signiﬁcant recent effort in genetic programming has focused on selecting and combining candidate solutions

according to a notion of behaviour deﬁned in semantic space and has also highlighted disadvantages of relying

on a single scalar measure to capture the complexity of program performance in evolutionary search. In this

paper, we take an alternative, yet complementary approach which directs crossover in what we call adjudicated

space, where adjudicated space represents an abstraction of program behaviour that focuses on the success or

failure of candidate solutions in solving problem sub-components. We investigate the effectiveness of several

possible adjudicated strategies on a variety of classiﬁcation and symbolic regression problems, and show that

both of our novel pillage and barter tactics signiﬁcantly outperform both a standard genetic programming and

an enhanced genetic programming conﬁguration on the fourteen problems studied.

1 BACKGROUND

Previously, research effort in directed crossover has

focused primarily on determining suitable crossover

points in genetic programming trees (GP) (Koza,

1990). See, for example (Langdon, 1995; Langdon,

1999).

One example of this effort can be seen with Con-

text Aware Crossover (CAC) which was proposed in

(Majeed and Ryan, 2006). In this method, after two

parents have been selected for crossover, one sub-tree

is randomly chosen in the ﬁrst parent and this sub-

tree is then crossed over into all possible locations in

the second parent and all generated children are eval-

uated. The best child (based on ﬁtness) is selected

and copied to the next generation. An advantage of

such context-based crossovers is increased probabil-

ity of producing children which are better than their

parents. On the other hand, it can be time consuming

to evaluate the context of each sub-tree.

The notion of a potentially unifying, repre-

sentation independent geometric crossover operator

was initially explored in (Moraglio and Poli, 2004;

Moraglio and Poli, 2005; Moraglio et al., 2006) in

which the authors proposed viewing solution space as

a geometric discrete space rather than a graph struc-

ture as was previously the norm. This new view

of solution space supports the concept of distance

by which we can imagine measuring somehow the

distance between candidate solutions in the solution

space or the distance between a solution and the

global maximum/minimum.

These ideas provided a platform for looking at ge-

netic operators such as crossover in a profoundly dif-

ferent way, where the emphasis is shifted away from

the structure of solutions and focuses instead on their

meaning as expressed by their semantics. Taking this

approach facilitates the measurement and utilisation

of distances in semantic space both between candi-

date solutions and between those solutions and the

desired target.

There is currently no deﬁnitive agreement on the

exact meaning of the term semantics in GP. However,

a fairly widely adopted one (Krawiec and Lichocki,

2009; Moraglio et al., 2012; Castelli et al., 2014),

which we also adopt here, is that the semantics of a

GP program is the vector of outputs that GP program

produces on training data: i.e. each value in the out-

put vector represents the result of evaluating the GP

program on a single training instance.

Semantically Driven Crossover (SDC) was sug-

gested in (Beadle and Johnson, 2008) in which they

applied a technique which removed redundant and

unreachable arguments from boolean GP programs

and produced Reduced Order Binary Decision Dia-

grams (ROBBDs) which could then be used to com-

pare program semantics. In that work, crossovers

were discarded unless the offspring were semantically

different from the parents. They reported superior per-

formance and less code bloat using SDC and observed

Fitzgerald, J. and Ryan, C..

For Sale or Wanted: Directed Crossover in Adjudicated Space.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 95-105

ISBN: 978-989-758-157-1

that bloat may be partially a result of intron creation

during crossover.

This ideas of SDC was extended for real val-

ued symbolic regression (SR) problems in (Nguyen

et al., 2009; Uy et al., 2009) which proposed Semantic

Aware Crossover (SAC), and investigated several pos-

sible scenarios in which they compared the semantics

of offspring with their parents, and depending on the

outcome accepted either or both offspring and/or par-

ents into the new population. They also examined the

effectiveness of a method which compared the seman-

tics of sub-trees at proposed crossover points, only ac-

cepting offspring into the new population if the sub-

trees were not semantically equivalent. They inves-

tigated SAC on several real-world SR problems and

concluded that the sub-tree approach was the most ef-

fective of those trials, and that SAC was a useful tech-

nique for maintaining diversity a GP population.

(Krawiec and Lichocki, 2009) developed an ap-

proach to semantic crossover that utilised a type of

brood recombination. In this method, called approx-

imately geometric semantic crossover (SX), a pool

of offspring is produced using sub-tree crossover for

each mating pair, and the offspring whose semantics

are closest to its parents is selected unless there is a

child with higher ﬁtness than both parents, in which

case it is selected regardless of semantics.

The alluring appeal of geometric semantic

crossover is that effective operators of this type can

provide a guarantee that the ﬁtness of the offspring

produced will be no worse than the ﬁtness of its par-

ent with the worst ﬁtness, providing the semantics of

the offspring lie between the semantics of its parents

in solution space. The challenge is to design opera-

tors that have this property but which are also usable

in practice. Against this background, Krawiec (Kraw-

iec, 2012) investigated two approaches for generat-

ing offspring GP individuals whose semantics are me-

dial (intermediate) with respect to the semantics of

their parents. Both methods concentrated on approx-

imating mediality by determining semantic similarity

of sub-programs and basing crossovers on that - an

approach that was much more computationally realis-

tic than trying to deal with whole programs.

A novel approach inﬂuenced by Quantitative

Genetics which the researchers called phenotypic

crossover was suggested in (Bassett et al., 2012).

This method aimed at maximising heritability by forc-

ing offspring to have similar traits to their ancestors.

The method delivered improved results over standard

GP on several problems.

(Naredo et al., 2013; Trujillo et al., 2013) adopted

a strategy which abstracted one or two levels beyond

semantic space into what they referred to as behaviour

space. They explored the idea of behaviour based

search using several binary classiﬁcation problems,

where rather than using an explicit ﬁtness function

they used open ended evolution guided by a type

of novelty search (NS) (Lehman and Stanley, 2008;

Lehman and Stanley, 2010). In this approach, selec-

tion was based on the relative novelty of individual

behaviour, where behaviour was represented by a bi-

nary descriptor. They experimented with two differ-

ent binary descriptors, each of which was a vector of

zeros and ones: one which captured whether the indi-

vidual correctly predicted each class label or not (ac-

curacy descriptor), and the other which captured the

predicted class labels (class descriptor). They re-

ported that NS outperformed standard GP on difﬁcult

problems but did slightly worse on trivial ones. Inter-

estingly, they also observed that their application of

NS seemed to eliminate or at least control bloat.

ESAGP (Error Space Alignment GP) was pre-

sented by (Ruberto et al., 2014) who explored mech-

anisms for ﬁnding compatible individuals based on

their alignment in error space. In other work, (Kraw-

iec and O’Reilly, 2014) have recently proposed be-

havioural programming GP (BPGP), an approach

which involves decomposing and archiving for later

use, sub-programs which have good utility, where

utility captures both the error of the sub-program and

its perceived usefulness according to a decision tree

methodology. They reported excellent results on a

wide variety of problems.

A closely related but quite different idea was ex-

plored by (Krawiec and Liskowski, 2015) who ap-

plied a clustering technique to test based problems.

Their Discovery of Objectives by Clustering (DOC)

system clustered GP programs together if they had

similar behaviour on the same test cases. They con-

structed interaction matrices, obtaining derived ob-

jectives to approximately represent this common be-

haviour and produce more effective search drivers.

The method was compared with several other opti-

mised GP algorithms and was shown to deliver statis-

tically better results on a range of problems.

The notion of behaviour space has its origins in

the area of robotics research (Brooks, 1999) for which

the terminology would seem to be eminently suitable.

We propose to further reﬁne and unify the terminol-

ogy for GP such that behaviour space as deﬁned in

(Naredo et al., 2013; Trujillo et al., 2013) is decom-

posed into semantic space, result space and adjudi-

cated space. In this view, taking classiﬁcation as an

example, result space maps to the class descriptor de-

scribed in (Naredo et al., 2013) and adjudicated space

to the accuracy descriptor. With regard to symbolic

regression, result space is equivalent to error space as

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

described in (Ruberto et al., 2014).

An exhaustive description of the relevant literature

is beyond the scope of this paper. For in depth re-

views of semantic approaches the reader is directed to

(Pawlak et al., 2014) and to (Vanneschi et al., 2014).

2 ADJUDICATED GP (AGP)

Our method is analagous to the process of selective

breeding (sometimes called artiﬁcial or unnatural se-

lection), whereby humans breed animals or plants for

certain traits – typically in order to domesticate them.

We have studied the effectiveness of our proposed

approach on both classiﬁcation and SR problems. The

strategy is essentially the same for both tasks, but

is, of necessity, slightly more complex in the case of

symbolic regression. For the moment, we will explain

the basic method as it applies to classiﬁcation and de-

fer description of symbolic details for later.

If we take a hypothetical example of a binary clas-

siﬁcation problem using GP, where each candidate so-

lution is evaluated on the same ten problem instances.

Supposing we have an individual which produces the

semantics shown in Figure 1 and we apply a threshold

whereby if the semantic is <= 50 the instance is clas-

siﬁed as belonging to class 1 and otherwise to class 2.

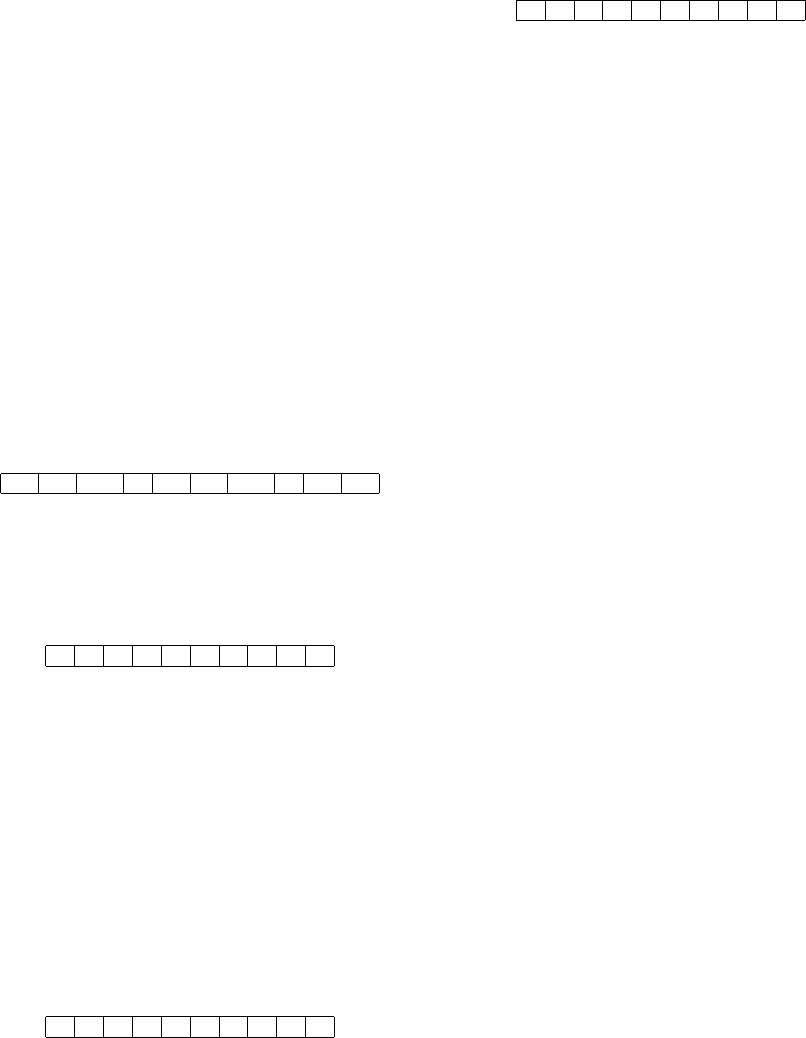
10 23 126 4 78 33 279 8 67 22

Figure 1: Semantic descriptor.

This thresholding gives rise to the result descriptor

shown in Figure 2, where 0 represents instances of

class 1 and 1 represents instances of class 2.

0 0 1 0 1 0 1 0 1 0

Figure 2: Result descriptor.

Now, if we consider the ground truth for the 10 in-

stances as shown in Figure 3, we can adjudicate, i.e

make a judgement on the success or failure of our hy-

pothetical individual on each problem instance, re-

sulting in the adjudicated descriptor shown in Fig-

ure 4. The adjudicated representation provides a ﬁne

grained view of individual performance compared to

a scalar ﬁtness value such as classiﬁcation accuracy.

We can easily imagine that even for a ten instance

problem there may be many individuals with exactly

the same ﬁtness score, each of whom are correctly

classifying a different set of instances.

1 1 1 1 1 0 0 0 0 1

Figure 3: Ground Truth.

As Krawiec et al. (Krawiec and O’Reilly, 2014)

pointed out, the reliance on a scalar ﬁtness value to

drive evolution “may be crippling because one cannot

expect difﬁcult learning and optimization problems to

be efﬁciently solved by heuristic algorithms that are

driven by a scalar objective function which provides

low-information feedback”.

0 0 1 0 1 1 0 1 0 0

Figure 4: Adjudicated Descriptor.

With this in mind, we choose to pursue the goal of

effectively navigating the solution space by focusing

on program behaviour in adjudicated space. We are

not concerned with program syntax or representation

- simply on identifying which GP programs can solve

which problem instances and using this information

to determine a mating strategy.

Thus, for each individual we decompose its ad-

judicated descriptor into a for sale list which is a list

identifying the problem instances that it is able to cor-

rectly predict and a wanted list which details those in-

stances which it has failed to correctly predict. See

Figures 5 and 6.

In traditional GP approaches, individuals are se-

lected for mating based on ﬁtness, where very unﬁt

individuals usually have very limited opportunities to

participate in crossover. In contrast, much of the re-

search effort outlined in section 1 explores various

strategies for ﬁnding pairs or groups of individuals

which are well-matched. according to some measure

of semantic compatibility before combining them to

produce new candidate solutions. Similar to other re-

cent work on semantic aware crossover, we choose to

explore the idea that it is more important that individ-

uals are compatible in other, potentially more impor-

tant ways than ﬁtness.

The system that we propose simpliﬁes the search

for compatible mates by focusing on individual be-

haviour in adjudicated space. Once an adjudication

has been made based on an individual’s results, and

the for sale and wanted lists have been populated, we

can select a mate for that individual by choosing a

prospective partner whose for sale list advertises the

ability to solve instances that are on its wanted list.

As long as all individuals are adjudicated in the

same way, if the for sale list of an individual contains

a reference to an instance which is on the wanted list

of another, then that pair of individuals are deﬁned to

be compatible to some degree.

As we have already described, the adjudication pro-

cess for classiﬁcation tasks is quite straightforward

regardless of the number of classes: each semantic

is converted into a result (predicted class label) and

For Sale or Wanted: Directed Crossover in Adjudicated Space

Table 1: Symbolic Regression Benchmarks.

Where X is one of 20 values uniformly distributed

between −1 and + 1.

Name Description

Nyg2 (Uy et al., 2011) X

+ X

Nyg3 (Uy et al., 2011) X

+ X

Nyg4 (Uy et al., 2011) X

+ X

this is judged to be correct or incorrect – for sale or

wanted. The process is slightly more complicated for

symbolic regression problems as the notion of cor-

rectness is not as clear cut. There are various ways

that this issue could be approached including, for ex-

ample, using the idea of “hits” where some deﬁned

minimum level of error on a training instance con-

stitutes a hit. Preliminary experiments conﬁrmed the

intuition that setting the threshold value too low was

unhelpful, particularly early in the evolutionary pro-

cess. Thus we choose to use the population median

mean absolute error (MAE) as the threshold for de-

termining whether an instance is put on the for sale or

wanted list. That is, for a given individual, if its error

for a given training instance is less than the popula-

tion median error for that instance it is adjudicated as

being a success and the ﬁtness case is put on the in-

dividual’s for sale list, whereas if the error is greater

than or equal to the population median error, the in-

dividual is adjudicated to have failed on that ﬁtness

case and the instance is put on the wanted list. This

is an aspect that requires further experimentation and

analysis.

2 4 5 7

Figure 5: For Sale List.

0 1 3 6 8 9

Figure 6: Wanted List.

Once the for sale and wanted lists have been created

for each individual in the population, there are proba-

bly many different strategies which could be adopted

in order to maximise compatibility. For this prelim-

inary study we have chosen to explore two different

strategies which we call pillage and barter. Each

of these strategies aims to ﬁnd a mating pair which

are approximately optimally compatible according to

slightly differing objectives.

2.1 Pillage

The pillage method is a selﬁsh strategy whereby for

each individual the system seeks out and chooses that

mate which offers the best return in terms of satisfy-

ing the wanted list of the ﬁrst individual. For both SR

and classiﬁcation tasks, the wanted list is compared

with the for sale list of every other individual and the

individual which has greatest number of elements in

the intersection of the two lists is selected.

2.2 Barter

As the name suggests, the barter approach is a more

congenial strategy whereby each participating indi-

vidual has the opportunity to gain from the transac-

tion. When the barter tactic is employed, directed

crossover only happens if each prospective parent lists

instance/s on their for sale list which the other has on

their wanted list.

At each generation the compatibility of each in-

dividual with every other individual is determined

by calculating a barter rate which is analogous to

the balanced accuracy measure used in classiﬁcation.

Similar to the pillage approach, the mate with highest

compatibility is selected.

2.3 MuLambda GP (mlGP)

For the mlGP conﬁguration crossover and mutation

operate as for stdGP, however the selection process is

slightly different: similar to the selection method ex-

plained in (Deb et al., 2002) where µ individuals from

the initial population are used to generate λ offspring,

and the best µ individuals from the entire µ + λ pool

are selected to form the new population. In this in-

stance λ = 2 ∗ µ; each crossover operation produces

two offspring.

2.4 AGP Selection

In traditional GP a mating pool is often created by pre-

selecting individuals according to some selection al-

gorithm. Tournament selection is a popular approach,

whereby the larger the tournament the more elitist the

selection process. We do not consider this method

appropriate for Adjudicated GP (AGP) as the overall

ﬁtness score of any individual is largely irrelevant for

the purpose of directing crossover. For example, we

can easily imagine that an otherwise unﬁt individual

may have the capability to correctly solve some small

set of ﬁtness cases. Thus, each individual in the pop-

ulation has the opportunity to participate in crossover

events and we perform post selection at each genera-

tion, once mating is completed.

This is achieved by adopting a µ + λ approach

similar to the mlGP method outlined above: a pop-

ulation of µ candidate solutions is used to produce a

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

Table 3: Classiﬁcation Benchmarks (Bache and Lichman, 2013).

Dataset Acronym Instances Attributes Classes

Blood Transfusion BT 684 3 2

Liver Disorders BUPA 256 6 2

Caravan Insurance CAR 5946 85 2

German Credit GC 750 25 2

Haberman’s Survival HS 255 4 2

Ionosphere ION 348 35 2

Parkinsons Disease PK 195 22 2

Wisconsin Breast Cancer WBC 452 9 2

Iris IR 150 4 3

Vertebral Column VC 310 6 3

Wine WN 178 9 3

Table 2: GP Parameters. For classiﬁcation problems a tour-

nament size of 3 applies to standard and Mu Lambda (ML)

experiments whereas tournaments of 7 candidates were

used for the AGP setups.

Parameter Value Value

Problem Type Classiﬁcation SR

Population Size 200 200

Max. Generations 30 250

Max Init depth 6 6

Max Depth 16 16

Tournament Size 3/9 7

Crossover Prob. 0.9 0.9

Mutation Prob. 0.1 0.1

Evolutionary Model Generational Generational

pool of λ new individuals consisting of parents and

offspring, from which µ individuals are chosen by

tournament selection to form the next generation. In

the current implementation λ = 2 ∗ µ; each individual

program participates in crossover with its compatible

mate and each crossover, which occurs at a predeter-

mined probability, produces two offspring.

3 EXPERIMENTAL ANALYSIS

We choose to compare our proposed AGP variants

(pillage and barter) with a standard GP (stdGP) set-

up. In addition, and in order to isolate any poten-

tial effects we also compare with a basic µ + λ ap-

proach (mlGP) to determine if the selection strategy

confers any beneﬁts in and of itself.

3.1 Problems

We have selected several well known classiﬁcation

and symbolic regression benchmark problems on

which to evaluate our proposed method. Classiﬁca-

tion problems consist of eight binary and three multi-

class problems with varying numbers of instances and

attributes as outlined in Table 3, whereas the three

symbolic regression tasks chosen are described in Ta-

ble 1.

3.2 Parameters

Details of the function sets used are shown in Table 4.

Note that constants are not used for any of the prob-

lems studied. Details of other relevant parameter set-

tings are detailed in Table 2.

Table 4: Function sets used. Division, log, exp are pro-

tected.

Type Function Set

Classiﬁcation +,−,∗,/

Symbolic Regression +,−,∗,/,sin,cos,log,exp,neg

For the regression tasks the objective function aims to

minimise MAE, whereas for all of the classiﬁcation

problems balanced accuracy is the objective function

which the system strives to maximise. Balanced ac-

curacy also known as Average accuracy which is a

well know performance measure used in classiﬁca-

tion. This method modiﬁes the calculation for overall

accuracy to better emphasise the performance of each

individual on each class as shown in Equation 1. The

true positive (TP) rate is the proportion of positive

instances which the individual classiﬁes as positive,

whereas the true negative (TN) rate is the proportion

of negative instances which are classiﬁed as negative.

The false positive (FP) and false negative (FN) rates

are the proportions of negatives which are wrongly

classiﬁed as positive and the proportion of positive

instances which are incorrectly classiﬁed as negative.

Generally, positive and negative instances correspond

to instances of the minority and majority classes re-

spectively.

BalAcc = 0.5 ∗



T P

(T P + FN)

T N

(T N + FP)



(1)

For Sale or Wanted: Directed Crossover in Adjudicated Space

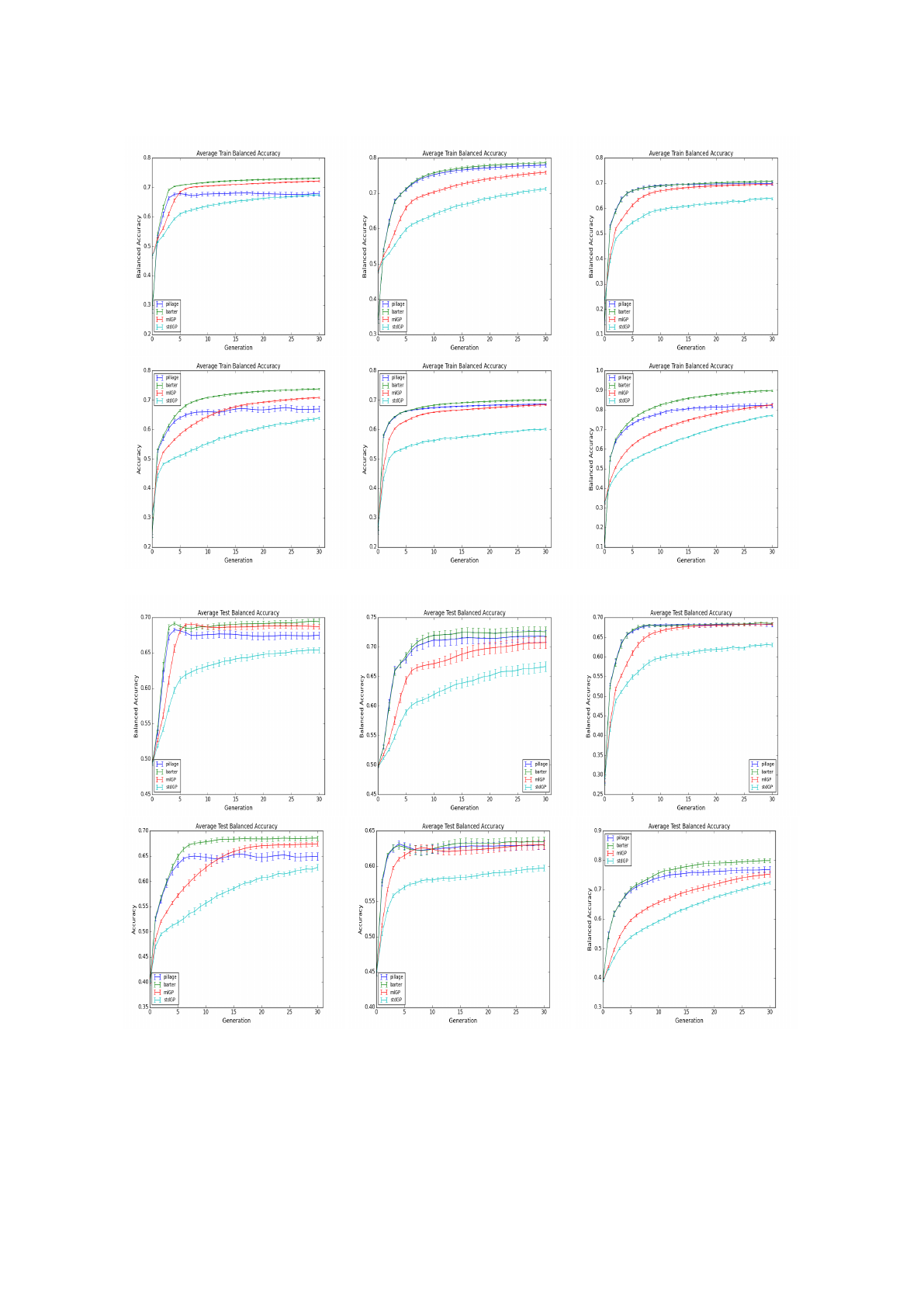
Figure 7: Balanced Training Accuracy for (from top to bottom and left to right) BT, BUPA, CAR, GC, HS and ION data.

Figure 8: Balanced Test Accuracy for (from left to right) BT, BUPA, CAR, GC. HS and ION data.

3.3 Results

For classiﬁcation benchmarks we report the average

training and test balanced accuracy and the program

size. Looking at the plots in Figures 7 to 10 we can

see that a consistent pattern emerges: the Barter ap-

proach produces the best performance on all of

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

100

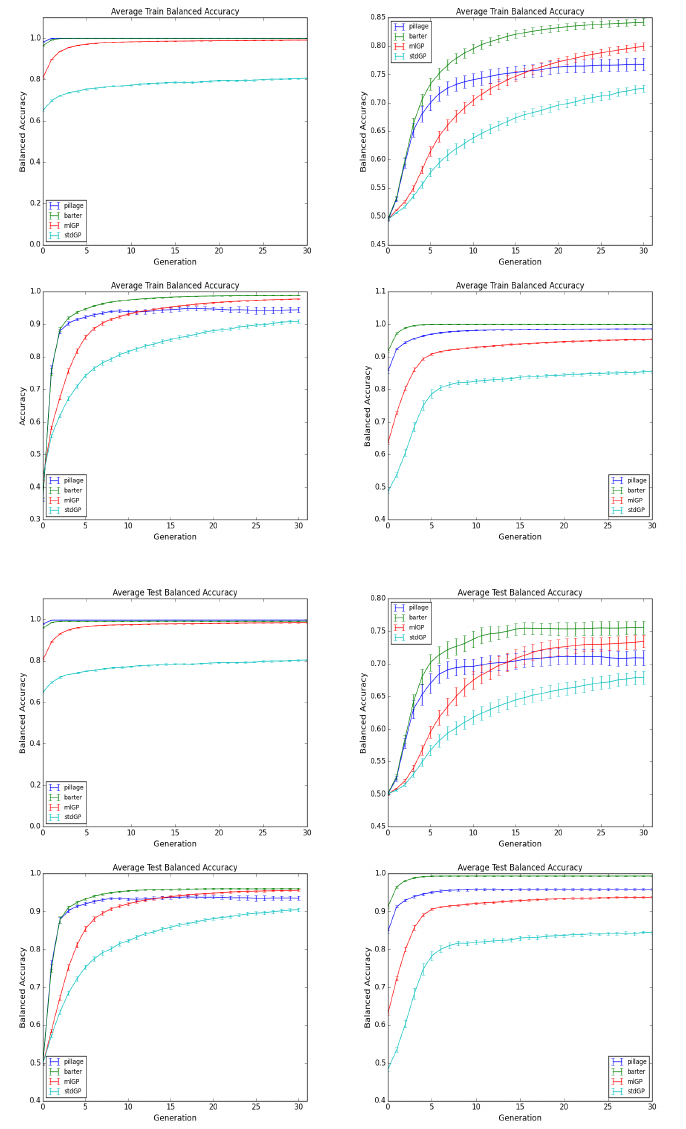
Figure 9: Training Accuracy for (from left to right) IRIS, PARK, WBC and WINE data.

Figure 10: Test Accuracy for (from left to right) IRIS, PARK, WBC and WINE data.

the benchmarks studied and stdGP delivers the weak-

est results overall. While the success of the barter

approach compared to pillage is philosophically sat-

isfying it is nevertheless somewhat surprising given

that there is almost inevitably a compromise associ-

ated with using the barter method. Interestingly, the

For Sale or Wanted: Directed Crossover in Adjudicated Space

101

Figure 11: Average Program Size for (from left to right, top to bottom) BT, BUPA, CAR, GC, HS, ION, IRIS and PARK data.

mlGP set-up produces results which are much better

than stdGP.

Turning our attention to the symbolic regression

tasks we report both the number of successful runs

together with the median MAE of the best of run in-

dividuals in Table 5. We use the same criteria for a

successful run as in (Uy et al., 2011) which deﬁnes a

successful run as one where any individual scores hits

on all ﬁtness cases – where a hit occurs when the ab-

solute error is less than 0.01 for a single ﬁtness case.

Looking at the results in Table 5 we can see that, simi-

lar to the classiﬁcation performances, of the two AGP

conﬁgurations, the Barter conﬁguration delivers su-

perior results in terms of the number of successful

runs on all three problems, also outperforming both

stdGP and mlGP, having almost twice as many suc-

cessful runs as stdGP on all problems. When it comes

to average MAE the situation is reversed, with both

stdGP and mlGP producing the lowest median error,

although the difference is not signiﬁcant.

3.3.1 Program Size

For all of the classiﬁcation problems studied pro-

gram growth during evolution was much more mod-

est when either of the AGP variants were employed

as can be seen in Figure 11. Of course, there is some

computational cost to the proposed AGP method as

compatibility has to be determined for each prospec-

tive mate. However, this is strongly mitigated by the

fact that solutions evolved using AGP are signiﬁcantly

smaller than those produced by stdGP or mlGP.

Smaller solutions are also produced by the AGP

methods for the SR problems. This may partly be ex-

plained by the fact that evolution terminates if a per-

fect solution is found, and there are more of these dis-

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

102

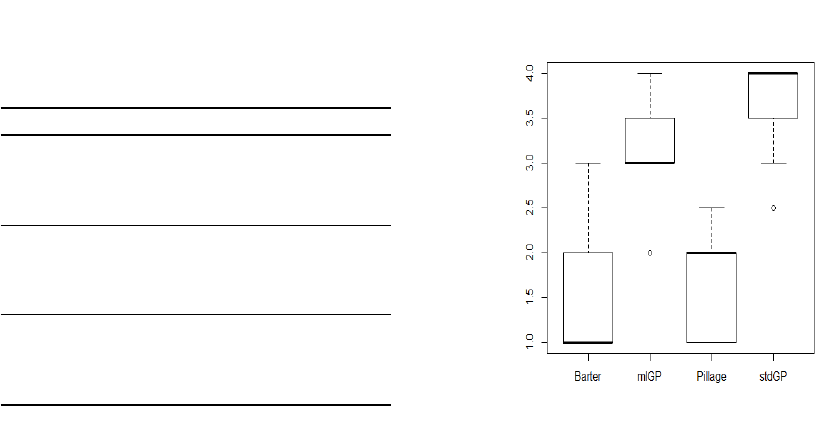
Table 5: Correct solutions, median error and nodes used for,

best-of-run individuals over 100 evolutionary runs.

Method Correct Median MAE Nodes

Nyg2

Barter 33 0.02 70.9

Pillage 20 0.02 63.3

mlGP 18 0.02 72.4

stdGP 16 0.02 95.6

Nyg3

Barter 20 0.03 84.0

Pillage 9 0.03 81.1

mlGP 8 0.02 97,2

stdGP 6 0.02 88.1

Nyg4

Barter 13 0.03 67.5

Pillage 13 0.03 64.1

mlGP 1 0.02 103.2

stdGP 4 0.02 108.7

covered during AGP runs. Thus, one possible reason

for smaller solutions is that the average size may be

smaller when there are more early terminations.

Aside from the empirical evidence we do not cur-

rently have any solid explanation as to why solutions

evolved using AGP are so much smaller than those

produced using the canonical GP on the classiﬁca-

tion problems. However, we can hypothesise that the

targeted nature of the method may reduce the possi-

bility of intron development. In this regard, we note

the similarity with the behaviour reported in (Trujillo

et al., 2014) and also in (Beadle and Johnson, 2008).

To determine statistical signiﬁcance, we carried

out the non-parametric Friedman test which is re-

garded as a suitable test for the empirical comparison

of the performance of different algorithms (Dem

sar,

2006) as shown in Figure 12. Using this approach,

which does not simply count wins, but rather takes

into account the relative performance of each algo-

rithm compared with every other algorithm on all of

the problems tackled, makes it easier to gain a clear

insight into which are most effective. Results demon-

strated that the AGP barter approach performed sig-

niﬁcantly better than the other methods investigated

on the selected benchmarks as post-hoc tests pro-

duced very small p-values (0.002 and 0.00006) for

the differences between it and mlGP and stdGP re-

spectively. A p-value of 0.003 was reported for the

difference between pillage and stdGP.

4 CONCLUSIONS

The evidence we have presented in this study suggests

that AGP, which operates in adjudicated space for

selection of compatible candidate solutions (for the

purpose of recombination) is a promising methodol-

Figure 12: Friedman plot of test accuracy on classiﬁcation.

Methods ranked from 1 to 4 where 1 is better.

ogy for evolutionary computation – performing con-

sistently well across the range of benchmarks studied.

This preliminary work would seem to demonstrate

that the method offers several useful advantages: it is

relatively simple to implement; produces small pro-

grams showing no evidence of bloat and, most impor-

tantly, is independent of the chosen representation.

As this is very much a preliminary study, we are

not able to provide any theoretical guarantees as to the

likely performance of AGP on problems other than

those presented in this investigation. As a next step,

we will examine the mechanics and theoretical un-

derpinnings of the method in greater detail. We will

also investigate several other adjudication strategies

for SR problems.

REFERENCES

Bache, K. and Lichman, M. (2013). UCI machine learning

repository.

Bassett, J., Kamath, U., and De Jong, K. (2012). A new

methodology for the GP theory toolbox. In Soule,

T. et al., editors, GECCO ’12: Proceedings of the

fourteenth international conference on Genetic and

evolutionary computation conference, pages 719–726,

Philadelphia, Pennsylvania, USA. ACM.

Beadle, L. and Johnson, C. (2008). Semantically driven

crossover in genetic programming. In Wang, J., ed-

itor, Proceedings of the IEEE World Congress on

Computational Intelligence, pages 111–116, Hong

Kong. IEEE Computational Intelligence Society,

IEEE Press.

Brooks, R. A. (1999). Cambrian intelligence: the early

history of the new AI. Mit Press.

Castelli, M., Vanneschi, L., and Silva, S. (2014). Prediction

of the uniﬁed parkinson’s disease rating scale assess-

ment using a genetic programming system with ge-

For Sale or Wanted: Directed Crossover in Adjudicated Space

103

ometric semantic genetic operators. Expert Systems

with Applications, 41(10):4608–4616.

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

Nsga-ii. Evolutionary Computation, IEEE Transac-

tions on, 6(2):182–197.

Dem

sar, J. (2006). Statistical comparisons of classiﬁers

over multiple data sets. The Journal of Machine

Learning Research, 7:1–30.

Koza, J. R. (1990). Genetic programming: A paradigm

for genetically breeding populations of computer pro-

grams to solve problems. Technical report.

Krawiec, K. (2012). Medial crossovers for genetic program-

ming. In Moraglio, A., et al., editors, Proceedings of

the 15th European Conference on Genetic Program-

ming, EuroGP 2012, volume 7244 of LNCS, pages

61–72, Malaga, Spain. Springer Verlag.

Krawiec, K. and Lichocki, P. (2009). Approximating geo-

metric crossover in semantic space. In Raidl, G., et al.,

editors, GECCO ’09: Proceedings of the 11th Annual

conference on Genetic and evolutionary computation,

pages 987–994, Montreal. ACM.

Krawiec, K. and Liskowski, P. (2015). Automatic deriva-

tion of search objectives for test-based genetic pro-

gramming. In Genetic Programming, pages 53–65.

Springer.

Krawiec, K. and O’Reilly, U.-M. (2014). Behavioral pro-

gramming: a broader and more detailed take on se-

mantic gp. In Proceedings of the 2014 conference

on Genetic and evolutionary computation, pages 935–

942. ACM.

Langdon, W. B. (1995). Directed crossover within genetic

programming. Research Note RN/95/71, University

College London, Gower Street, London WC1E 6BT,

UK.

Langdon, W. B. (1999). Size fair and homologous tree

genetic programming crossovers. In Banzhaf, W., et

al., editors, Proceedings of the Genetic and Evolution-

ary Computation Conference, volume 2, pages 1092–

1097, Orlando, Florida, USA. Morgan Kaufmann.

Lehman, J. and Stanley, K. O. (2008). Exploiting open-

endedness to solve problems through the search for

novelty. In ALIFE, pages 329–336.

Lehman, J. and Stanley, K. O. (2010). Efﬁciently evolving

programs through the search for novelty. In Branke,

J., et al., editors, GECCO ’10: Proceedings of the

12th annual conference on Genetic and evolutionary

computation, pages 837–844, Portland, Oregon, USA.

ACM.

Majeed, H. and Ryan, C. (2006). Using context-aware

crossover to improve the performance of GP. In Kei-

jzer, M., et al., editors, GECCO 2006: Proceedings of

the 8th annual conference on Genetic and evolution-

ary computation, volume 1, pages 847–854, Seattle,

Washington, USA. ACM Press.

Moraglio, A., Krawiec, K., and Johnson, C. G. (2012). Ge-

ometric semantic genetic programming. In Coello

Coello, C. A., et al., editors, Parallel Problem Solv-

ing from Nature, PPSN XII (part 1), volume 7491

of Lecture Notes in Computer Science, pages 21–31,

Taormina, Italy. Springer.

Moraglio, A. and Poli, R. (2004). Topological interpre-

tation of crossover. In Deb, K., et al., editors, Ge-

netic and Evolutionary Computation – GECCO-2004,

Part I, volume 3102 of Lecture Notes in Computer Sci-

ence, pages 1377–1388, Seattle, WA, USA. Springer-

Verlag.

CEC Moraglio, A. and Poli, R. (2005). Geometric land-

scape of homologous crossover for syntactic trees. In

Proceedings of the 2005 IEEE Congress on Evolution-

ary Computation (CEC-2005), volume 1, pages 427–

434, Edinburgh. IEEE.

Moraglio, A., Poli, R., and Seehuus, R. (2006). Geomet-

ric crossover for biological sequences. In Collet, P., et

al., editors, Proceedings of the 9th European Confer-

ence on Genetic Programming, volume 3905 of Lec-

ture Notes in Computer Science, pages 121–132, Bu-

dapest, Hungary. Springer.

Naredo, E., Trujillo, L., and Martinez, Y. (2013). Searching

for novel classiﬁers. In Krawiec, K., et al., editors,

Proceedings of the 16th European Conference on Ge-

netic Programming, EuroGP 2013, volume 7831 of

LNCS, pages 145–156, Vienna, Austria. Springer Ver-

lag.

Nguyen, Q. U., Nguyen, X. H., and O’Neill, M. (2009). Se-

mantic aware crossover for genetic programming: The

case for real-valued function regression. In Vanneschi,

L., et al., editors, Proceedings of the 12th European

Conference on Genetic Programming, EuroGP 2009,

volume 5481 of LNCS, pages 292–302, Tuebingen.

Springer.

Pawlak, T. P., Wieloch, B., and Krawiec, K. (2014). Re-

view and comparative analysis of geometric semantic

crossovers. Genetic Programming and Evolvable Ma-

chines, pages 1–36.

Ruberto, S., Vanneschi, L., Castelli, M., and Silva, S.

(2014). ESAGP – A semantic GP framework based

on alignment in the error space. In Nicolau, M., et al.,

editors, 17th European Conference on Genetic Pro-

gramming, volume 8599 of LNCS, pages 150–161,

Granada, Spain. Springer.

Trujillo, L., Mu

noz, L., Naredo, E., and Mart

ınez, Y.

(2014). Neat, theres no bloat. In Genetic Program-

ming, pages 174–185. Springer.

Trujillo, L., Naredo, E., and Martinez, Y. (2013). Pre-

liminary study of bloat in genetic programming with

behavior-based search. In Emmerich, M., et al., ed-

itors, EVOLVE - A Bridge between Probability, Set

Oriented Numerics, and Evolutionary Computation

IV, volume 227 of Advances in Intelligent Systems

and Computing, pages 293–305, Leiden, Holland.

Springer.

Uy, N. Q., Hoai, N. X., O’Neill, M., McKay, B., and

Galvan-Lopez, E. (2009). An analysis of semantic

aware crossover. In Cai, Z., et al., editors, Proceedings

of the International Symposium on Intelligent Com-

putation and Applications, volume 51 of Communi-

cations in Computer and Information Science, pages

56–65. Springer.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

104

Uy, N. Q., Hoai, N. X., ONeill, M., McKay, R. I.,

and Galv

an-L

opez, E. (2011). Semantically-based

crossover in genetic programming: application to real-

valued symbolic regression. Genetic Programming

and Evolvable Machines, 12(2):91–119.

Vanneschi, L., Castelli, M., and Silva, S. (2014). A survey

of semantic methods in genetic programming. Genetic

Programming and Evolvable Machines, 15(2):195–

214.

For Sale or Wanted: Directed Crossover in Adjudicated Space

105