Metaheuristic Coevolution Workflow Scheduling in Cloud
Environment
Denis Nasonov, Mikhail Melnik, Natalya Shindyapina and Nikolay Butakov
E-Science Research Institute, ITMO University, Birzhevaya liniya 4, Saint-Petersburg, Russia
Keywords: Scheduling Algorithm, Coevolution, Workflow, Metaheuristic, Virtual Machine, Cloud Environment.
Abstract: Today technological progress makes scientific community to challenge more and more complex issues
related to computational organization in distributed heterogeneous environments, which usually include
cloud computing systems, grids, clusters, PCs and even mobile phones. In such environments, traditionally,
one of the most frequently used mechanisms of computational organization is the Workflow approach.
Taking into account new technological advantages, such as resources virtualization, we propose new
coevolution approaches for workflow scheduling problem. The approach is based on metaheuristic
coevolution that evolves several diverse populations that influence each other with final positive effect.
Besides traditional population, that optimizes tasks execution order and task's map to the computational
resources, additional populations are used to change computational environment to gain more efficient
optimization. As a result, proposed scheduling algorithm optimizes both computation tasks to computation
environment and computation environment to computation tasks, making final execution process more
efficient than traditional approaches can provide.
1 INTRODUCTION
Today technological progress makes scientific
community to challenge more and more complex
issues related to computational organization in
distributed heterogeneous environments, which
usually include cloud computing systems, grids,
clusters, PCs and even mobile devices (Boutaba and
Cheng, 2012). Day-by-day computational tasks also
increase their structure complicacy and
computational difficulty combining new multiscale
and multidiscipline approaches for resolving
complicated issues that are imposed by advanced
scientific researches. In such heterogeneous
environments, traditionally, one of the most
frequently used mechanisms of computational
organization is a Workflow approach (Yu and
Buyya, 2008). It allows to bring complex
computational logic in sequential order of executed
steps (tasks) linked by input\output data. Due to
resources and workflows heterogeneity, one of the
most important issues nowadays is the task
scheduling as an optimization problem.
Workflow scheduling optimization is NP-
complete problem and there are a lot of research
dedicated to this area. Most of them are based on
investigations of invented heuristic and
metaheuristic algorithms (Yu and Buyya, 2008), as
well as on hybrid schemas that take the best parts
from both types of algorithms in cooperation
(Nasonov and Butakov, 2014). Metaheuristic
algorithms include evolutionary methods that
contain coevolutionary approach (Back, 1996). In
spite of the fact that coevolutionary ideas were
proposed a half century ago (Ehrlich and Raven,
1964) a quite new ideas can be applied towards
workflow scheduling optimization problem.
One of the main parameters for the optimization
in workflow scheduling is makespan that shows the
amount of time from the start of workflow's
execution to its finish point. Traditionally scheduling
algorithms decrease makespan by proposing more
efficient task allocation on the available
computational resources. Moreover, in cloud
computing, cost of execution is also the significant
criteria for the scheduling. However, taking into
consideration advanced technologies like
virtualization, new opportunities can be found in the
field of workflow scheduling.
Combining distributed environments features
with workflow steps arrangement and resource
allocation within coevolutionary principles, we
propose the new approaches for workflow
252
Nasonov, D., Melnik, M., Shindyapina, N. and Butakov, N..
Metaheuristic Coevolution Workflow Scheduling in Cloud Environment.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 252-260
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
scheduling, which comply more to present-day
technologies (in the time of cloud computing) rather
than traditional schemas. We propose new
coevolution genetic algorithm (CGA), coevolution
particle swan optimization algorithm (CPSO) with
its ranked and weight ranked extensions’ (CRPSO
and CWRPSO), as well as coevolution gravity
search algorithm (CGSA) for workflow scheduling
problem in flexible cloud environment, where
computing resources can be modified according to
virtualization principles.
2 RELATED WORKS
Palacios et al. (Palacios, 2014) proposed hybrid
coevolutionary genetic algorithm (GA) called CELS
for fuzzy flexible job shop scheduling problem with
heuristic initialization step and additional local
species improvement during fitness evaluation.
Definition of the problem and developed methods
are similar to workflow scheduling problem in the
use of mapping and ordering species.
Coevolutionary implementation includes mapping
and ordering species, which form cooperative
populations. However, in our approach the first
population optimizes both mapping and ordering,
while the second population selects an optimal
resources configuration. Also Palacios et al.
proposed a different approach for coevolution fitness
evaluation with other selection strategy - species
coupling is organized according to the best, random,
and individual rank.
Huang et al. (Huang and Chen, 2014) offered
two coevolutionary algorithms based on GA for job
shop scheduling problem with different methods of
subpopulation merging. Coevolutionary scheme is
based on full task dimension splitting to three
subpopulations, thus decreasing the dimensionality
of each new population. Whereas our populations
develop according to the task characteristic
diversity. Huang’s work is focused on the selection
methods of subpopulations. The first proposed
CCGA scheme is based on greedy (by fitness)
individual selection from other population while the
second DBCCGA computes the distance between
individuals and chooses the one from another
population according to the obtained distances.
Multi-population PSO (Particle Swarm
Optimization) for flow shop scheduling problem was
suggested by Liu et al (Liu, 2013). The main idea of
this paper is to divide full population into three
populations at each iteration and apply different
optimization strategies for each population. At the
merging stage the best particles from each
subpopulation are used to build a probabilistic model
by EDA (Exploratory Data Analysis) and after that
to improve the particles, SA (Simulated Annealing)
is applied locally to these particles.
In the next work, Jiao et al. (Jiao and Chen,
2011) proposed Cooperative Coevolution PSO based
on the catastrophe for fuzzy flow shop scheduling
problem. Extended catastrophe operation helps to
avoid local optima. Their coevolution interpretation
as in the previous works contrasts with our approach
in the division of a population into subpopulations.
Verma et al. (Verma and Kaushal, 2014)
proposed Bi-criteria priority algorithm based on
PSO for workflow scheduling. Their algorithm is
hybrid of HEFT (Heterogeneous Earliest Finish
Time) heuristic and PSO meta-heuristics. HEFT is
used to obtain an order of tasks while PSO is applied
for tasks’ assignment optimization. The makespan
and total cost of result schedule are the main
optimization criteria in the paper whereas we
consider only the makespan. However, their particle
is represented only by task assignment, and ordering
of a schedule is performed by Budget HEFT.
The Revised Discrete PSO for cloud workflow
scheduling is proposed by Wu et al (Wu, 2010). In
this paper authors proposed the bi-criteria
optimization of makespan and total cost with
initialization by greedy heuristic GRASP algorithm.
In comparison to our work, their particle
representation contains an ordered vector of pairs
(task, node) and particle update is performed only by
mapping. During PSO mapping update, the tasks are
taken sequentially, in respect to their inner
dependencies. Whereas in our work, mapping and
ordering are evaluated and updated separately.
Lei (Lei, 2012) offered coevolution GA for
fuzzy flexible job shop scheduling. Although
merging scheme is different to our scheme, this
work is similar in used concepts of coevolution and
partially has similar representations of the different
species. The algorithm performs selection based on
the artificial population of a scheduled solution
while we perform a selection only on population of
the same species and the selection of different
species can be independent.
Gu et al. (Gu, 2010) proposed algorithm to
resolve scheduling problem in the field of stochastic
job shop scheduling based on GA. According to
experiments, their method outperforms standard
widely applied GA and some of its modifications. In
contrast to our cooperative scheme, besides the field
of application, authors use a competitive coevolution
scheme.
Metaheuristic Coevolution Workflow Scheduling in Cloud Environment
253
Flexible Job shop scheduling problem is solved
by using Gravitational Search Algorithm and
Colored Petri Net by Barzegar et al. (Barzegar and
Motameni, 2012). In comparison to several other
algorithms, proposed method exceeds these
algorithms in a work speed and efficiency of
solutions. However, authors considered job shop
scheduling problem, while our work is concerned
with workflow scheduling using coevolution
principles for the population.
3 COEVOLUTION PRINCIPLES
Applicability of coevolution methods can be found
in different areas of optimization problem.
Workflow scheduling is one of them. The main idea
we propose in this paper is hidden in dynamical
changes which can be done in the cloud
computational environment during execution
process. On the one hand, traditional algorithms try
to optimize workflow tasks execution order and
resource mapping, while the computation environ-
ment is specified by initial conditions. On the other
hand, almost all present public clouds are based on
advanced technologies like virtualization and
efficiently use it for energy and budget saving.
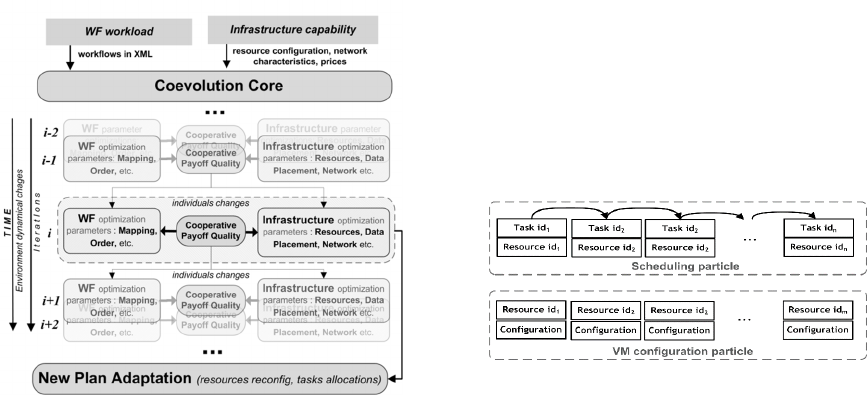
Figure 1: Common schema of coevolution approach for
workflow scheduling.
Taking together workflow resource allocation
from traditional scheduling optimization and
resource configuration optimization from advanced
technologies used in cloud computing, new level of
efficiency can be achieved. Coevolution idea allows
to execute several evolutionary process in parallel
binding them in cooperative manner. On figure 1 the
main coevolutionary schema is shown. On the left
part, traditional evolutionary process for resource
allocation is executed, and at the same time on the
right part evolutionary process of resource and data
reconfiguration is running. Composite solution
payoff quality is estimated on each iteration taking
into account both parts of evolutions. Parts are taken
according to the used selection strategy and gain
payoff quality from the best combination. The best
solution is chosen from the current iteration and
adapted to the system if it has more efficient
execution plan than currently used one.
3.1 Coevolution Genetic Algorithm
(CGA)
Scheduling coevolution genetic algorithm (CGA) is
built on the cooperation of several populations that
search optimized parts of the joint solution.
Resources allocation, tasks ordering, data placement
and resource configuration optimization can be
chosen in the role of those parts. Even traditional
GA implementation for workflow scheduling can be
divided in two evolutions: task mapping on
resources and task execution ordering. Each
evolution applies basic schema of crossover,
mutation, selection methods with one difference in
the fitness function that can estimate new scheduling
plans only using part’s combination (mapping and
ordering together). In (Butakov and Nasonov, 2014)
benefits of this approach were shown.
Another idea that can be used in GA is basic
scheduling evolution with computation environment
evolution together to get even more efficient
optimization.
Figure 2: Particles schema in CGA algorithm.
Thus, CGA scheme has two independent
populations. The first one optimize scheduling (tasks
assignment and their ordering), whereas the second
population optimize computing environment for
tasks. Since a full solution represents by pair of
particles from each population, CGA has additional
Merge step, on which populations interact between
each other to produce full solution pairs. The
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
254

number of produced pairs is an algorithm’s
parameter called interactions number, which should
be greater than populations’ size. After the Merge
stage, we can evaluate fitness function for produced
pairs. Each particle receive average fitness of all
pairs, where this particle had been. The next steps
are mutation and crossover for each population
separately.
Figure 3: Proposed CGA algorithm main schema.
Particles representation is shown on the figure 2.
Mutation for schedule particle is performed by two
options: swap two tasks in queue; or randomly
change computing resource for a task. We use 2-
points crossover to divide the first parent into
beginning, middle, and end. Child will contain
beginning and end from the first parent, and all other
not included tasks from the second parent.
Mutation for a configuration particle has three
options: delete resource; add resource; or change a
capacity of resource. Crossover is performed by
alternately selection of resources from two parents.
Tournament selection is used for both populations.
Fitness function for all our algorithms is makespan.
3.2 Coevolution Particle Swarm
Optimization (CPSO)
PSO is the metaheuristic algorithm proposed by
Kennedy and Eberhart (Eberhart and Kennedy,
1995), idea of which was taken from birds flocking
or fish schooling. To find an optimal solution, each
particle in the swarm flies according to the personal
experience and information about the global best
position for whole population. The movement of a
particle is defined by its position and velocity, which
are updated in each generation. The equations for
velocity and position update of the i-th particle are:
(
+1
)
=
(
)
+
−
(
)
+
(−
(
)
)
(1)
(
+1
)
=
(
)
+
(+1)
(2)
where t is current generation, w is the inertia
coefficient for previous velocity, c
1
and c
2
are
behaviour coefficients, which define the influence of
global best and personal best positions accordingly,
r
1
and r
2
are random variables in the range [0, 1]. p
i
is the best position for the current particle and g is
the global best position for the whole population.
PSO was created for a continuous optimization.
To implement PSO for combinatorial space, it is
required to define set-based operators between
particles and their velocities for computation (1) and
(2).
In contrast to other works (Wu, 2010) or (Verma
and Kaushal, 2014), our schedule particle
representation (figure 2) contains mapping and
ordering parts, which allow to generate a more
qualitative schedule. In addition, we considered
several modifications of basic coevolution PSO
scheme to get a broader view of this problem.
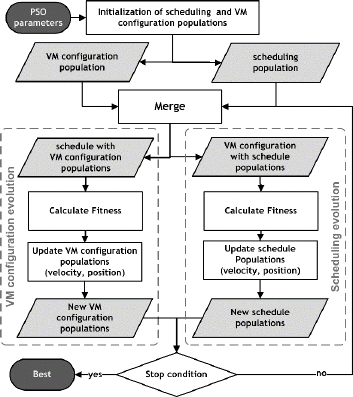
Scheme of developed CPSO is shown in figure
4. On the first step, populations are initialized. The
first population (Scheduling population) includes
particles with mapping and ordering abilities, which
are responsible for final tasks scheduling
optimization while the second population (VM
configuration population) is made of particles that
optimize nodes' configuration. On the next step, the
populations are merged to obtain individuals for
fitness evaluation. To complete the Merge step, n
particles from one population form pairs with n
particles from the other population. For each pair the
fitness is calculated and then two of the log best
pairs are selected randomly. The first pair is chosen
as a scheduling particle for the configuration
population and the second one is chosen for
schedule population. In addition, the best pair is
checked for the new global best.
After the Merge stage, each population is ready
to calculate the fitness for each particle. At the next
step, the particles update their velocity and position,
according to equations (1) and (2). The last stage is
checking all particles for the new best solution. If
the Stop condition is not satisfied, the populations
Metaheuristic Coevolution Workflow Scheduling in Cloud Environment
255
are moved to the next generation. Operators for
particles update will be discussed below. These
operators are needed to compute (1) and (2).
Let ={
}
– set of tasks, and ={
}
-
set of computing nodes.
Figure 4: Proposed CPSO algorithm main schema.
3.2.1 Mapping Particle
Mapping particle is represented as a set of pairs of
tasks and assignment nodes, that determines which
task will run on which node. Position
of particle
is
={
,
}
, and velocity
={
,
,
},
where
is value in range
[
0,1
]
. It should be noted,
that position
contains elements with all tasks from
, while velocity
may contains not all tasks or
elements with the same task, but with different
nodes.
The first operation is (-) between two particles
and
returns a velocity of
toward to
performs via difference of sets:
→
=
−
=
\
, that is set of
{
,
,1
}
,
where pairs
{
,
}
∈
∉
with the value =
1 for each pair.
The next operation (·) for velocity
and
constant :
⋅={
,
,
⋅}
The sum (+) of two velocities
and
can be
estimated as follows:
+
=∪{
,
,(
,
)}, i.e. the union
of velocities with the max value, if velocities contain
the same pair (
,
).
The last operation is position update (2), which
presented by sum (+) of position
and velocity
, where is current iteration. Firstly we generate
random value in range [0, 1]. After that, we
compute trimmed velocity
by cut all elements
from
with values
< , i.e.
=
{
,
,
>
}
, where pairs (
,
)∈
. A new
position
performs by random node selection
from
for each task
.
=
+
=
{
,(
))}.
3.2.2 Ordering Particle
Ordering particle determines the order of task
execution. Position of particle
is represented as a
={
,
}
, where
is values in range [-1, 1].
Tasks queue is determined by sorting these values in
the ascending order. On initialization phase we sort
tasks by their start time of the current solution, and
are assigned for each task depending on the index
in the sorted tasks list:
=−1+∙2/, =
1... As in the mapping particle, we shall define
operations for (1) computing:
(-):
→
=
−
={
,
−
}
(·):
∙c={t
,q
∙c}
(+):
+
={
,
+
}
and (2):
(+):
=
+
={
,
+
}
After evaluation of new particle position by use
PSO equations (1) and (2) and operations, which
mentioned above, we can construct new tasks queue
by sort the tasks by their values in the ascending
order.
3.2.3 Configuration Particle
Above we had defined operations for both parts of
schedule particle (mapping and ordering parts). Now
we will describe operations to compute (1) and (2)
for particles from configuration population. All
computing nodes have maximum capacity .
Position
and velocity
of particle
are list
of nodes’ capacities:
=[
]
;
=
[
]
. This representation define number of
resources and their capacities.
Operations for (1):
(-):
−
=
−
, if |
|≠|
|,
than smaller vector is complemented by zeros.
(·):
∙c=[cap
∙c]
(+):
+
=[
+
]
And for (2):
(+):
=
+
=[
+
]. After
computing we shall remove elements with not
positive
=< 0, and divided elements with
> into several elements
(
)
(
−
). Thus, our configuration particle, beside the
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
256
possibility of change nodes capacity, also has
possibility to reduce or increase number of nodes.
3.2.4 Coevolution Ranked PSO Modification
The coevolution ranked PSO (CRPSO) modification
of ordering particle is based on the predefined
ranked list. This rank list with the ranks for each task
can be constructed by HEFT or another list based
algorithm. Rank list is represented as a set of tasks
and their ranks:
= {
,
=(
)}
. These ranks
are required to define task by values at particle build
step.
Particle’s position
and velocity
are
represented as an ordered list of values:
=
[
]
;
=[
]
. At the initialization step,
these values in
are determines as ranks of tasks
from rank list.
Operations to evaluate (1):
(-):
−
=[
−
]
(·):
∙c=[q
∙c]
(+):
+
=[
+
]
And (2):
(+):
=
+
=[
+
]
On the build step, we should encode this list of
values into the tasks queue. To do that, for each
in this list we find a value in the rank list with
min(|
−[
]|)and choose task .
3.2.5 Coevolution Weight Ranked PSO
Modification
Coevolution weight ranked PSO (CWRPSO) is
modification of the node selection operation in the
mapping part. In the general scheme a new
assignment node for each task is chosen randomly
from all nodes in the velocity, without relations
between tasks. In this case, for each task a new
assignment node is chosen from the velocity’s pairs
(
,
) with the same task, depending on the
velocity's values of these pairs. This method allows
particles to move more directly to the other particles.
However, particles have more chances to trap into a
local optimum.
3.3 Coevolution Gravitation Search
Algorithm (CGSA)
The gravitation search algorithm is proposed by
Rashedi (Rashedi E., Nezamabadi-Pour, 2009). Idea
of method is based on the law of gravity. The
algorithm is similar to PSO in particles motion. The
main equation for the force computation:
=
=()
(
(
)
−
())
(3)
, where () is the gravitational constant,
and
are the masses of particles, and R is the distance
between the particles.
Equations for position and velocity update of
particle :
(
+1
)
=
(
)
+
()
(4)
, where
(
)
is number of best particles, which
are used to update other particles.
(
)
() are decreasing through the time.
(
+1
)
=∙
(
)
+∙
( +1)
(5)
GSA is differ to PSO in additional step of computing
masses. Masses can be evaluated by:
() =
() −()
(
)
−()
(6)
, where
() – fitness of particle
at iteration
, and
(
)
() are the best and the worst
finesses of population at iteration . The same
scheme (figure 4) and operators are used as in CPSO
with all corresponding modifications. In compare to
PSO, GSA has more possibility to avoid local
optimums, since particles’ velocities depend on
kbest particles, while in PSO velocities depend only
on two: and particles.
4 EXPERIMENTAL STUDY
In order to verify the efficiency of the proposed
algorithms, we conducted experiments with CGA,
CPSO, CRPSO, CWRPSO and CGSA. According to
internal experiments with CGSA modifications, we
have left only CWGSA as the best one.
As the experimental environment own
implemented simulator was used. In each
experiment, a final makespan was calculated as a
result of average value that is obtained from series of
1000 runs for each workflow. In addition, the
execution cost, which is also informative criteria in
the cloud environment, was considered as a
restriction for the set of resources. Algorithms were
executed on xml representation of workflows:
Montage, CyberShake, Inspiral, Sipht, Epigenomics
that were taken from (Pegasus, 2014) database with
different tasks count as traditional benchmark
workflows (Yu and Buyya, 2008). The Montage
with 25, 50, 75, 100 tasks and the CyberShake with
30, 50, 75, 100 tasks were left as the most
representative. Computational cost of each task is
Metaheuristic Coevolution Workflow Scheduling in Cloud Environment
257
determined by its runtime, which is an attribute that
is contained in the workflow’s xml file.
Computational resource is represented by a value of
its capacity in arbitrary units. For experimental study
to keep balance in a set of resources we assume two
following rules: maximum resource’s capacity is 30
and the total capacity sum of all resources must be
80. The transfer cost for any two different resources
is set to constant value 100. Each task is computed
only on one resource at one single moment of a time.
For a fair play, all experiments were conducted
in same conditions of population size and
generations’ count. To improve efficiency of the
algorithms, in all cases initial populations have one
particle, generated by heuristic HEFT algorithm.
Experiments were performed with the following
parameters: population size is 100, generations count
is 300 and interactions count is 200. For CGA
crossover probability 0.3, mutation probability 0.5,
and selection method is tournament. In all CPSO
cases the inertia coefficient w is 0.5 and behaviour
coefficients c1 and c2 are 1.6 and 1.2 respectively.
For the last CGSA type of algorithms inertia w =
0.2, acceleration coefficient c = 0.5, initial kbest and
G are 10. The results are presented in the tables 1
and 2.
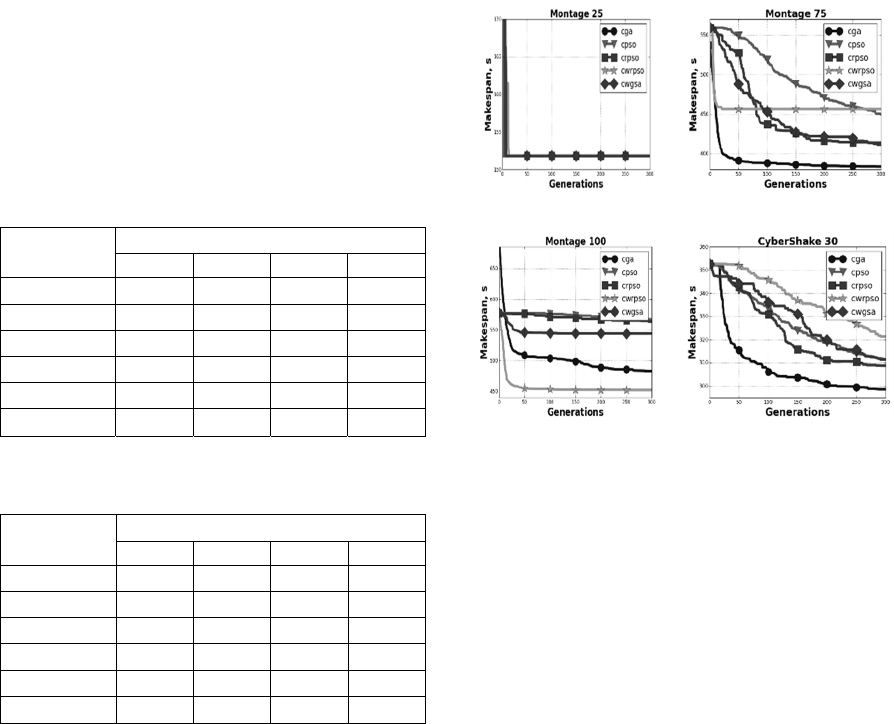
Table 1: Makespan for each Montage workflow and each
introduced algorithm.
Algorithm
Montage makespan in sec
M_25 M_50 M_75 M_100
HEFT
280 345 559 578
CGA
152 264 371 467
CPSO
152 296 450 566
CRPSO
152 297 414 563
CWRPSO
152 340 456 452
CWGSA
152 295 411 544
Table 2: Makespan for each Cybershake workflow and
each introduced algorithm.
Algorithm
Cybershake makespan in sec
CS_30 CS_50 CS_75 CS_100
HEFT
353 485 652 909
CGA
298 452 620 893
CPSO
311 481 651 909
CRPSO
309 479 649 908
CWRPSO
321 460 638 896
CWGSA
311 467 650 904
It can be clearly seen that HEFT produces worse
results than results obtained by proposed schemas. It
confirms suitable performance capabilities of
developed algorithms. It is evident, that CGA
produced better results in almost all workflows
scheduling. It overcomes with up to 82% HEFT
algorithms and with up to 11% all other
metaheuristics (for M_50 experiment). What is more
curious, CPSO beats CGA in the M_100 case (467
against 452, figure 5(c)), that confirms absence of an
absolute leader.
We can found that CRPSO modification was
better than basic CPSO algorithm, and better than
CWRPSO in most cases. Moreover, we can see on
figure 5 (b, c), that CWRPSO has high convergence
speed, however, has not possibility to avoid local
optimums. Thus, CWRPSO can be useful, if
algorithm is limited with execution time and have to
produce solution on the first iterations. Despite that,
CWGSA does not win in any cases, we can see from
figure 5, that CWGSA produces a stable average
result among all the other algorithms.
(a) (b)
(c) (d)
Figure 5: Fitness function improvement for the workflows.
4.1 CGA Parameter Analysis
In order to find the best parameters for CGA
algorithm experimental studies were performed for
different workflow scenarios. To explore the
influence of particle mutation and crossover
probability, following range of probability values
were selected: 10, 20, .., 90%. Other parameters
were set to: 1) count of interaction individuals – 200;
2) count of generations – 300.
In the experiment, scheduling algorithm was
executed for all studied workflows. The final
summarised results are presented on figure 6
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
258

Figure 6: Makespan aggregated rate. (The lowest values
corresponds to the closest values to the global optimal
solution).
(contour plot). We can observe several local
minimum areas (3 points with around ~7.6%), but
the global minimum can be found at the point (30%,
50%). It has the average result 4.5% worse than the
global optimum for each separated result for each
workflow and each pair of probability values.
5 CONCLUSIONS
In this paper three coevolution metaheuristic
algorithms were compared. As it can be observed
from the experimental results of the proposed
algorithms, the coevolution idea of binding together
traditional scheduling algorithm with technological
advantages can be quite productive, especially in the
terms of resource dynamic virtualization. The results
can achieve up to 84% of performance increasing in
comparison to HEFT algorithm as well as for the
best CGA approach performance increases up to
11% in comparison to the other metaheuristics.
Summarizing, we can say that CGA is the most
effective algorithm in compare to CPSO and CGSA
schemes, due to its combinatorial nature. CPSO
algorithms are the most diverse and not stable.
However, they have greater convergence speed and
can provide better solution in limited time. CWGSA
is not the most successful algorithm, but more
stable, than CPSO schemes. However, there is a
great field for new investigations related to
algorithms behaviour analysis in dynamically
changing environments, data-intensive computation
cases, hyperheuristic approach as well as schemas
methods improving.
REFERENCES
Boutaba R., Cheng L., Zhang Q. On cloud computational
models and the heterogeneity challenge //Journal of
Internet Services and Applications. – 2012. – Т. 3. –
№. 1. – С. 77-86.
Yu J., Buyya R., Ramamohanarao K. Workflow
scheduling algorithms for grid computing
//Metaheuristics for scheduling in distributed
computing environments. – Springer Berlin
Heidelberg, 2008. – С. 173-214.
Nasonov D., Butakov N. Hybrid Scheduling Algorithm in
Early Warning Systems //Procedia Computer Science.
– 2014. – Т. 29. – С. 1677-1687.
Back T. Evolutionary algorithms in theory and practice. –
Oxford Univ. Press, 1996.
Ehrlich P. R., Raven P. H. Butterflies and plants: a study
in coevolution //Evolution. – 1964. – С. 586-608.
Palacios J. J. et al. Coevolutionary makespan optimisation
through different ranking methods for the fuzzy
flexible job shop //Fuzzy Sets and Systems. – 2014.
Huang M., Chen J., Sun B. A new collaborator selection
method of cooperative co-evolutionary genetic
algorithm and its application //Multisensor Fusion and
Information Integration for Intelligent Systems (MFI),
2014 International Conference on. – IEEE, 2014. – С.
1-6.
Liu R. et al. A multipopulation PSO based memetic
algorithm for permutation flow shop scheduling //The
Scientific World Journal. – 2013. – Т. 2013.
Jiao B., Chen Q., Yan S. A cooperative co-evolution PSO
for flow shop scheduling problem with uncertainty
//Journal of computers. – 2011. – Т. 6. – №. 9. – С.
1955-1961.
Verma A., Kaushal S. Bi-Criteria Priority based Particle
Swarm Optimization workflow scheduling algorithm
for cloud //Engineering and Computational Sciences
(RAECS), 2014 Recent Advances in. – IEEE, 2014. –
С. 1-6.
Wu Z. et al. A revised discrete particle swarm
optimization for cloud workflow scheduling
//Computational Intelligence and Security (CIS), 2010
International Conference on. – IEEE, 2010. – С. 184-
188.
Lei D. Co-evolutionary genetic algorithm for fuzzy
flexible job shop scheduling //Applied Soft Computing.
– 2012. – Т. 12. – №. 8. – С. 2237-2245.
Gu J. et al. A novel competitive co-evolutionary quantum
genetic algorithm for stochastic job shop scheduling
problem //Computers & Operations Research. – 2010.
– Т. 37. – №. 5. – С. 927-937.
Barzegar B., Motameni H., Bozorgi H. Solving flexible
job-shop scheduling problem using gravitational
search algorithm and colored Petri net //Journal of
Applied Mathematics. – 2012. – Т. 2012.
Eberhart R. C., Kennedy J. A new optimizer using particle
swarm theory //Proceedings of the sixth international
symposium on micro machine and human science. –
1995. – Т. 1. – С. 39-43.
Topcuoglu H., Hariri S., Wu M. Performance-effective
and low-complexity task scheduling for heterogeneous
computing //Parallel and Distributed Systems, IEEE
Transactions on. – 2002. – Т. 13. – №. 3. – С. 260-
274.
Metaheuristic Coevolution Workflow Scheduling in Cloud Environment
259
Rashedi E., Nezamabadi-Pour H., Saryazdi S. GSA: a
gravitational search algorithm //Information sciences.
– 2009. – Т. 179. – №. 13. – С. 2232-2248.
Butakov N., Nasonov D. Co-evolutional genetic algorithm
for workflow scheduling in heterogeneous distributed
environment //Application of Information and
Communication Technologies (AICT), 2014 IEEE 8th
International Conference on. – IEEE, 2014. – С. 1-5.
Pegasus. (n.d.). Retrieved from Workflow Management
System: http://pegasus.isi.edu/
Nasonov D. et al. Hybrid Evolutionary Workflow
Scheduling Algorithm for Dynamic Heterogeneous
Distributed Computational Environment
//International Joint Conference SOCO’14-CISIS’14-
ICEUTE’14. – Springer International Publishing,
2014. – С. 83-92.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
260
