Neurosolver Learning to Solve Towers of Hanoi Puzzles

Andrzej Bieszczad and Skyler Kuchar

Computer Science, California State University Channel Islands, One University Drive, Camarillo, CA 93012, U.S.A.

Keywords: Neural Network, Neurosolver, General Problem Solving, Search, State Spaces, Temporal Learning, Neural

Modeling, Towers of Hanoi.

Abstract: Neurosolver is a neuromorphic planner and a general problem solving (GPS) system. To acquire its problem

solving capability, Neurosolver uses a structure similar to the columnar organization of the cortex of the brain

and a notion of place cells. The fundamental idea behind Neurosolver is to model world using a state space

paradigm, and then use the model to solve problems presented as a pair of two states of the world: the current

state and the desired (i.e., goal) state. Alternatively, the current state may be known (e.g., through the use of

sensors), so the problem is fully expressed by stating just the goal state. Mechanically, Neurosolver works as

a memory recollection system in which training samples are given as sequences of states of the subject system.

Neurosolver generates a collection of interconnected nodes (inspired by cortical columns), each of which

represents a single point in the problem state space, with the connections representing state transitions. A

connection map between states is generated during training, and using this learned memory information,

Neurosolver is able to construct a path from its current state, to the goal state for each such pair for which a

transitions is possible at all. In this paper we show that Neurosolver is capable of acquiring from scratch the

complete knowledge necessary to solve any puzzle for a given Towers of Hanoi configuration.

1 INTRODUCTION

The goal of the research that led to the original

introduction of Neurosolver, as reported in

(Bieszczad and Pagurek, 1998), was to design a

neuromorphic device that would be able to solve

problems in the framework of the state space

paradigm. Fundamentally, in this paradigm, a

question is asked how to navigate a system through

its state space so it transitions from the current state

into some desired goal state. The states of a system

are correspond to points in an n-dimensional space

where each dimension is a certain characteristics of

the system. Trajectories in such spaces formed by

state transitions represent behavioral patterns of the

system. A problem is presented in this paradigm as a

pair of two states: the current state and the desired, or

goal, state. If a sensory system is used, then the

problem can be stated by just indicating the desired

state, since the current state is detected by the sensors.

A solution to the problem is a trajectory between the

two points in the state space representing the current

state and the goal state.

Neurosolver can solve such problems by first

building a behavioral model of the subject system and

then by traversing the recorded trajectories during

both searches and resolutions (Bieszczad, 2006;

2007, 2008, 2011). This processes will be described

with more detail in the following sections. The

learning is probabilistic, so in many respects this

approach is similar to Markov Models (Markov,

2006). However, in some cases, any solution is a good

solution, so rather than acquiring a behavioral model

of the subject system, a random process can be used

to detect all possible transitions between any two

states. For example, paths can be constructed in a

maze through allowing an artificial rat driven by a

Neurosolver-based brain to explore the limits of the

maze (e.g., the walls) (Bieszczad, 2007).

In this paper, we demonstrate that Neurosolver

can solve Towers of Hanoi puzzles with three towers.

Conceptually, exactly same approach would be taken

for any number of towers; we discuss that at the end

of the paper. We explore the probabilistic aspects of

the models for this particular application, and observe

that they do not bring significant gains in

functionality, while slowing down the efficiency of

the searches. As could be expected, puzzles with

larger number of disks require significantly more

training steps to explore all valid trajectories in the

state space. Nevertheless, allowing Neurosolver to

explore the state space sufficiently guarantees that the

best solution is found for any puzzle.

Bieszczad, A. and Kuchar, S..

Neurosolver Learning to Solve Towers of Hanoi Puzzles.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 3: NCTA, pages 28-38

ISBN: 978-989-758-157-1

1.1 Inspirations from Neuroscience

The original research on Neurosolver modeling was

inspired by Burnod’s monograph on the workings of

the human brain (Burnod, 1988). The class of systems

that employ state spaces to present and solve

problems has its roots in the early stages of AI

research that derived many ideas from the studies of

human information processing; among them on

General Problem Solver (GPS) (Newell and Simon,

1963). This pioneering work led to very interesting

problem solving (e.g. SOAR (Laird, Newell, and

Rosenbloom, 1987)) and planning systems (e.g.

STRIPS (Nillson, 1980).

Neurosolver employs activity spreading

techniques that have their roots in early work on

semantic networks (e.g., (Collins and Loftus, 1975)

and (Anderson, 1983)).

1.2 Neurosolver

Neurosolver is a network of interconnected nodes.

Each node represents a state in the problem space.

Rather than considering all possible states of the

subject system, Neurosolver generates nodes only for

states that were explicitly used during the training,

although in principle, in future some hardware

platforms could be easier to implement with

provisions for all states rather than creating them on

demand. In its original application, Neurosolver is

presented with a problem by two signals: the goal

associated with the desired state and the sensory

signal associated with the current state. A sequence of

firing nodes that Neurosolver generates represents a

trajectory in the state space. Therefore, a solution to

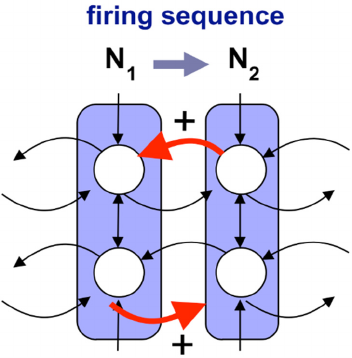
Figure 1: Neurosolver learning rule.

the given problem is a succession of firing nodes

starting with the node corresponding to the current

state of the system, and ending with the node

corresponding to the desired state of the system.The

node used in Neurosolver is based on a biological

cortical column (references to the relevant

neurobiological literature can be found in (Bieszczad

and Pagurek, 1998)). In this simplified model, the

node, an artificial cortical column, consists of two

divisions, the upper and the lower, as illustrated in

Figure 1. The upper division is a unit integrating

internal signals from other upper divisions and from

the control center providing the limbic input (i.e., a

goal or — using a more psychological term — a

drive, or desire, that is believed to have its origins in

the brain’s limbic system). The activity of the upper

division is transmitted to the lower division where it

is subsequently integrated with signals from other

lower divisions and the thalamic input (i.e., the signal

from the sensory system that is relayed through the

brain’s thalamus; for example, a visual system that

recognizes the current configuration of the Towers of

Hanoi puzzle). The upper divisions constitute a

network of units that propagate search activity from

the goal, while the lower divisions constitute a

network of threshold units that integrate search and

sensory signals, and subsequently generate a

sequence of firing nodes; a resolution of the posed

problem (see Figure 2). The output of the lower

division is the output of the whole node.

The function of the network of upper divisions is

to spread the search activity along the intra-cortical

(i.e., upper-to-upper division) connections (as shown

in Figure 3) starting at the original source of activity:

the node associated with the goal state that receives

the limbic input (representing what is desired). This

can be described as a search network because the

activity spreads out in reverse order from that node

along the learned trajectories in hope to find a node

that receives excitatory thalamic input that indicates

that the node corresponds to the current state of the

system. At that node, the activities of the upper and

lower divisions are integrated, and if the combined

activity exceeds the output threshold, the node fires.

The firing node is the trigger of a resolution. The

resolution might be only one of many, but due to the

probabilistic learning it is best in the sense that it was

the most common in the training.

The process of spreading activity in a search tree

is called goal regression (Nillson, 1980). The

implementation on a digital computer is discrete in

that it follows the recalculations of states in cellular

networks. Double-buffering is used to hold the

Neurosolver Learning to Solve Towers of Hanoi Puzzles

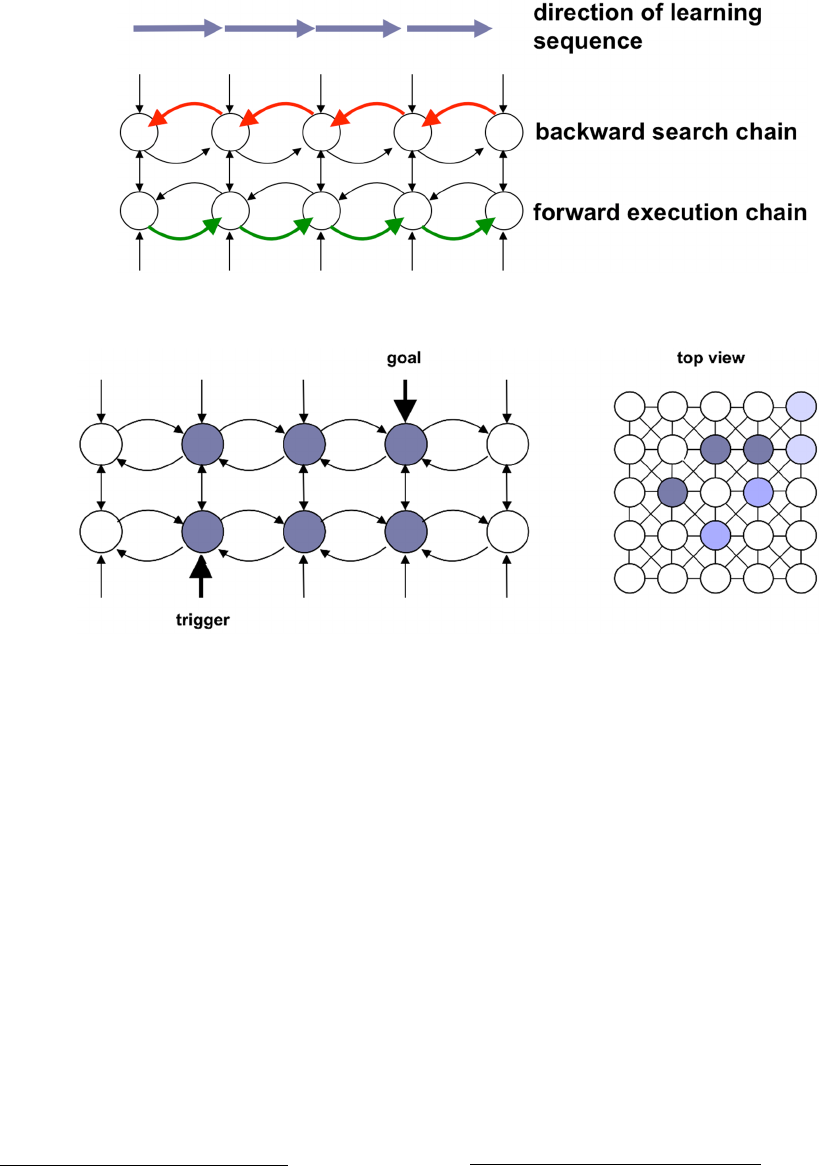
Figure 2: Learning state space trajectories through bi-directional traces between nodes corresponding to transitional states of

the system.

Figure 3: Search in Neurosolver. The externally induced activity is propagated from the node representing the goal state along

the connections between the upper divisions of the nodes in the reverse direction to the direction in which the training samples

were presented. All such pathways are branches in the search tree.

current state of Neurosolver

at some time tick t,

while the next state at time tick t+1 is calculated; the

buffers are swapped after that is complete

The purpose of the network composed of lower

divisions and their connections is to generate a

sequence of output signals from firing nodes (along

the connections shown in Figure 5). Such a sequence

corresponds to a path between the current state and

the goal state, so it can be considered a solution to the

problem. As we said, a firing of the node representing

the current state triggers a solution. Each subsequent

firing node sends action potentials through the

outgoing connections of its lower division. These

signals may cause another node to fire especially if

that node’s attention (i.e., the activity in the upper

division; also called expectation) is sufficiently high,

as that may indicate that the node is part of the search

tree. In a way, the process of selecting the successor

It is important not to confuse the states of Neurosolver

with the states of the subject system that Neurosolver is

modeling.

in the resolution path is a form of selecting the node

most susceptible to firing. A firing node is inhibited

for some time afterwards to avoid oscillations. The

length of the inhibition determines the length of

cycles that can be prevented.

Neurosolver exhibits goal-oriented behavior

similar to that introduced in (Deutsch, 1960).

The strength of every inter-nodal connection is

computed as a function of two probabilities: the

probability that a firing source node will generate an

action potential in this particular connection and the

probability that the target node will fire upon

receiving an action potential from the connection (as

shown in Equation 1).

To compute the probabilities, statistics for each

division of the node (both the upper and the lower)

and each connection are collected as illustrated in

Figure 5. The number of transmissions of an action

In theory, alternate implementations — for example

utilizing hardware to propagate analog signals — could be

more efficient, but at the moment are hard to realize in

practice.

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications

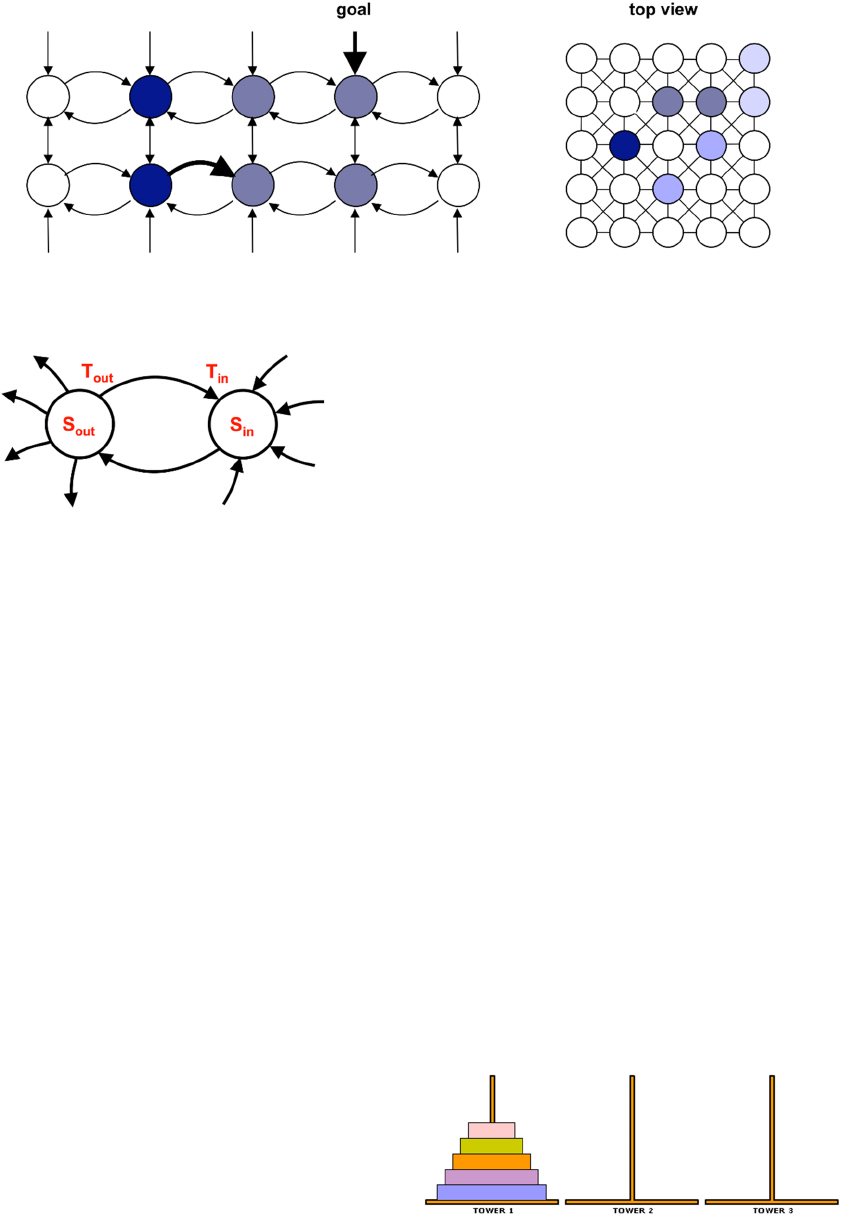
Figure 4: Resolution in Neurosolver. When the search activity integrates with the thalamic input in the node representing the

current state of the system, it triggers a chain reaction of firing nodes towards the node representing the desired — goal —

state, from which the search activity in the upper divisions had originated.

Figure 5: Statistics collected for computation of the

connection strength between nodes.

potential (i.e., transfer of the activity between two

divisions) T

out

is recorded for each connection.

The total number of cases when a division positively

influenced other nodes S

out

is collected for each

division. A positive influence means that an action

potential sent from a division of a firing node to

another node caused that second node to fire in the

following time tick. In addition, statistical data that

relate to incoming signals is also collected. T

is the

number of times when an action potential transmitted

over the connection contributed to the firing of the

target node and is collected for each connection. S

collected for each division, is the total number of

times when any node positively influenced the node.

With such statistical data, we can calculate the

probability that an incoming action potential will

indeed cause the target node to fire. The final formula

that is used for computing the strength of a connection

(shown in Equation 1) is the likelihood that a firing

source node will induce an action potential in the

outgoing connection, multiplied by the likelihood that

the target node will fire due to an incoming signal

from that connection:

P = P

out

= (T

out

) (T

/ S

) (1)

1.3 Problem: Towers of Hanoi

Towers of Hanoi puzzle is a problem of moving a set

of disks between a pair of pegs (“towers”) utilizing

one or more auxiliary pegs with the rule that a larger

disk can never be placed on top of a smaller disk. A

generalized versions of the problem is to transition

between any two disk configurations observing the

same rules. The former is just a specific version of the

latter, so in this paper we consider the generalized

version of the puzzle.

Commonly, three towers are used in the puzzles;

however, that number can also be generalized. For

example, a puzzle with four towers is called Reve’s

puzzle. While there are known algorithms to find best

solutions to puzzles (i.e., the transition between the

start configuration and the goal configuration with the

minimal disk moves), there is no known algorithm

that can deal with the exponential explosion of

complexity for problems with larger number of disks.

There exists a presumed solution (Stewart, 1941); its

correctness is based on Frame-Stewart conjecture and

has been verified for four towers with up to 30 disks.

In this paper, we deal with puzzles with three

towers. A version with 5 disks is shown in Figure 6.

2 IMPLEMENTATION

Towers of Hanoi puzzle (often also called game) fits

very well into the state space paradigm: each disk

configuration corresponds to a state in the game state

space, and a path between any two points in the state

Figure 6: The Towers of Hanoi puzzle with three towers.

Neurosolver Learning to Solve Towers of Hanoi Puzzles

space is a solution to a puzzle for which these two

states are the starting and the goal states. Depending

on the number of disks the state space might be larger

or smaller, but the fit for the paradigm is not affected.

A question then arises if Neurosolver that is

designed to work with problems posed in the terms of

state spaces can indeed be used to tackle Tower of

Hanoi game problems.

2.1 Modeling Towers of Hanoi

In our implementation, each state of the puzzle is

represented as a string as the following examples

show:

•

3 disks: [000,000,123]

•

4 disks: [0012,0003,0004]

•

5 disks: [12345,00000,00000] (see Figure 6)

Here, each tower is represented by n numbers,

separated by a comma where n represents the number

of disks. The example string with 5 disks (n=5)

represents the configuration shown in Figure 4. The

goal state of all disks on peg 3 would be

[00000,00000,12345]. This method of encoding the

state of the game is simple yet also uniquely readable

and convenient as input to Neurosolver. Such

representation could be easily obtained using a

number of methods; for example applying image

processing potentially with some machine learning

techniques for classification. Such preprocessing is

outside of the scope of this paper, so we assume that

the input data are already in this format.

The hypothesis is that after training, Neurosolver

will be able to solve any puzzle problem; i.e., find a

path in the state space of the puzzle going from any

state A, to the goal state B, that can also be any of the

states. Typically the goal is to start with all disks in

tower 1, and move all of them to tower 3; the stated

hypothesis encompasses such a specific case.

Figure 7 shows a partial state space of a puzzle

with three towers and three discs. Only valid states

and valid transitions are shown in the diagram.

2.2 Modeling Neurosolver

Neurosolver consists of a collection of nodes

representing the configurations of the Tower of Hanoi

game.

Each node has two parts, an upper division, which

contains connections for searching, and a lower

division, which contains connections for actually

solving a problem. The upper level can also be

considered the desire, or goal part of the node,

whereas the lower level represents the current

configuration (as determined by the sensory input) as

well as a controller for forcing disk moves that are

required to get to the goal configuration. Each node

representing a single configuration is connected to

one or more nodes representing other valid

configurations. Neurosolver training is the process of

building nodes corresponding to configurations that

are encountered in the training samples and

constructing a connection map between the nodes.

The connections represent moves of a single disk.

As explained earlier, the connections can have

associated weights that vary based on parameters

such as transitional frequencies, however as we will

see, this does not affect the functional effectiveness

of the model in solving Towers of Hanoi problems.

Figure 7: A partial state space for Towers of Hanoi puzzle with three towers and three discs. Only valid states are included;

i.e., the states that can be reached observing the puzzle rules.

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications

2.3 Neurosolver Operation

Neurosolver requires three main stages to solve a

problem:

• training,

• searching, and

• solving.

2.3.1 Training

Training is responsible for generating state nodes and

for building the connection map between subsequent

states observed in training sequences. This can be

done through various types of training, with a

common approach of Neurosolver exploring actual

transitions between states. For this research, we

implemented two methods of training, user-guided,

and random.

In user-guided training, the system just lets the

user play the game, while it records all moves that the

user makes. While this supervised training is very

effective and can capture user’s experience, it is also

extremely slow (and tedious to the expert player) for

all but the smallest state spaces. While the system will

capture and generalize user’s experience, there will

be no explorations for unknown solutions. There is

also exposure to user mistakes in both entering

invalid configurations and suboptimal resolutions. In

that respect, that approach is similar to building an

expert system through knowledge acquisition from

presumed experts. As with expert systems, the

expertise is captured, but there is no guarantee that

best, or even good, solutions are found; simply, the

experts may not know them.

To get much wider exploration of possible

solutions, perhaps unknown to any users (“experts”),

a random training was implemented. In this mode, in

the spirit of stochastic search methods, random but

still valid moves between puzzle configurations (i.e.,

moves that do not violate the rules of the game) are

generated and input to Neurosolver. It then records all

state transitions as inter-nodal connections.

It should be emphasized again that the training

only creates connections between nodes that

correspond to states that were observed; there are

neither nodes nor connections for states that were

never entered. For example, any invalid state does not

have a representation in Neurosolver. If two states are

theoretically connected, but were not part of any

training sample, then Neurosolver will not use this

theoretical link to solve a problem, as it doesn’t know

of such a connection. Hence, in random mode, it is a

prerogative to allow ample time for space

explorations to capture all possible — and valid —

transitions.

There is a profound functional difference between

the models built with two training techniques: the

former (user-guided) is a probabilistic model that

captures preferred solutions; the latter (random)

builds a connection map, but the statistical

observations need to be ignored as they are also

random.

The models built with both techniques generalize

and optimize solutions by potentially concatenating

parts of other paths into a novel solution. For

example, if a path between [123,000,000] and

[000,123,000], and a path between [000,123,000] and

[000,000,123] are both learned, then the system can

solve a problem [123,000,000]→[000,000,123] in

spite of never seeing such a training sequence.

Essentially, in the random method only singular state

transitions may be used in training.

In both training modes we allow selection of the

number of disks to use in the simulator. In the random

mode of training, the user additionally can select how

many training cycles should be used; in the user-

guided mode the number of training cycles is a

function of user’s tutoring persistence. The program

then returns how many states it managed to find out

of the theoretical total. As we can see in Figure 8, and

as no surprise, the larger the number of possible

states, the more training cycles are required.

This step could be much improved by training in

some controlled manner. The state space of the Tower

of Hanoi problem is fairly well structured, so any

controlled training scheme would give very good

results, but we wanted the process to be completely

unsupervised to explore Neurosolver’s capabilities to

capture the complete knowledge from scratch.

Figure 8 shows the effectiveness of the random

training with 1,000,000 training samples (i.e., single

state transitions).

2.3.2 Searching

After the training is complete, Neurosolver will have

built a connection map between numerous states of

the problem domain. The next step is to apply our

goal (”limbic” or desire) and current/start (“thalamic”

or sensory) inputs to the system. Using past

knowledge from training, the search phase is looking

for a plan that will be used to actually solve the given

problem.

The search mechanism is implemented by

traversing the upper level of the nodes (states) and

their connections. The idea behind the search, is that

our goal is our desire; here, the puzzle configuration

Neurosolver Learning to Solve Towers of Hanoi Puzzles

Figure 8: Output capture from Neurosolver shows the

performance of training Neurosolver with 1,000,000

training cycles on a fairly fast iMac (4 GHz Intel Core i7

with 4 cores and 32 GB RAM) using Python 3 with NumPy

version 1.9.2.

The search mechanism is implemented by

traversing the upper level of the nodes (states) and

their connections. The idea behind the search, is that

our goal is our desire; here, the puzzle configuration

that we want. We start from our desired goal state,

and begin to traverse the state space via our learned

connections (see Figure 9).

This is done via an activation value that is applied

to our goal state that is propagated along connections

to the neighboring nodes. Eventually, the hope is that

the spread of the activity will stimulate the node that

also receives the thalamic input to its lower level that

indicates the perceived current state. Once the

activation from the upper level and the lower level are

combined, the node will fire itself from the lower

level, subsequently projecting the activation to its

connected neighboring nodes. If any of the nodes at

the receiving side of these connections has both upper

and lower activation values, then that node will get

increase in the activity sufficient to fire; and so on and

so forth. This constitutes the third stage of

Neurosolver’s operation, the solving. Eventually the

lower level nodes will fire back to the goal. That will

have solved the problem as the goal node gets

inhibited, and consequently the source of the search

activity ceases.

Figure 9: The searching phase of Neurosolver’s operation.

This is a top view of the nodes. Compare with Figure 3 and

Figure 4.

To implement the search stage, a method similar

to cellular automata was used, where at each search

step, the activity of the current node is projected to all

connected nodes, but the activity of those nodes is

recalculated only in the following step (time tick). As

the system progresses through a number of goal

regression cycles, the activity is spread to increasing

number of connected nodes, essentially exploring all

learned paths concurrently in search of the node

associated with the current state.

The benefit of this approach is that it will find the

shortest solution that Neurosolver knows about, as all

possibilities are explored one step at a time. This also

means that any solutions that are close to our current

state will be found quickly.

The downside to this method is that for states that

are far from the goal state, Neurosolver will end up

iterating over many nodes. Depending on the state

space, this could increase dramatically.

One interesting note about searching in the

context of Neurosolver, is that the search is not

actually producing a specific path to the goal. Once

the start node is activated, we do not have a specific

solution. However, the solution is embedded into the

state of Neurosolver itself in the form of activation

values applied to its state nodes. Using this

information, we can construct a path from our start

node back to our goal! The search portion of

Neurosolver produces a directed search tree. Here, as

we traverse backwards through connections in the

upper level of the node, we produce a tree that can be

Disk Count: 1

States found: 3 out of 3 possible.

Runtime: 140.733876 sec

Disk Count: 2

States found: 9 out of 9 possible.

Runtime: 125.792373 sec

Disk Count: 3

States found: 27 out of 27 possible.

Runtime: 126.491495 sec

Disk Count: 4

States found: 81 out of 81 possible.

Runtime: 128.699436 sec

Disk Count: 5

States found: 243 out of 243 possible.

Runtime: 125.649405 sec

Disk Count: 6

States found: 729 out of 729 possible.

Runtime: 128.065042 sec

Disk Count: 7

States found: 2187 out of 2187 possible.

Runtime: 129.181981 sec

Disk Count: 8

States found: 6561 out of 6561 possible.

Runtime: 131.752802 sec

Disk Count: 9

States found: 19683 out of 19683 possible.

Runtime: 135.488318 sec

Disk Count: 10

States found: 48727 out of 59049 possible.

Runtime: 137.897707 sec

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications

used to generate the actual solution from the start

node to the goal node.

Now that we have our first phase complete with a

list of connections, and we have gone through the

searching portion and generated our search tree, we

can move to the final step in solving the problem.

2.3.3 Solving

The last stage of Neurosolver is to use all of the

information collected thus far, and to generate a

solution from the given current state to the specified

goal state.

During the search phase of Neurosolver’s

operation the activity has spread from the goal state

along all possible connections in the upper divisions.

Since the start state has enough activity from both the

upper division (as the result of the search) and lower

division (due to the sensory signal indicating the

current state of the system), it will cause the lower

level to fire, and subsequently excite its neighbor

nodes (along the connections in between the lower

divisions). Since both upper and lower division

activations are required for the lower division to fire,

only the nodes that contain upper division activation

will fire, and that’s only possible for the nodes that

are activated during the search phase. As each lower

division node fires to its neighbor nodes, only the

ones that are activated (i.e., are in an attentive state)

will be activated at levels sufficient to fire; so on and

so forth until the activity reaches the goal state at

which point the problem will have been solved. That

process is illustrated in Figure 10.

Figure 10: The solving phase of Neurosolver’s operation.

As stated earlier, the solving phase still doesn’t

actually give us a complete solution path; it just

causes a sequence of firing nodes. To actually solve

the problem we need to engage the firing of each node

as a trigger for an action that will force the solution

(such as, for example, printing a configuration

associated with the firing node, or, actually

transitioning the puzzle from configuration A to

configuration B in some virtual or real environment).

2.4 Optimizing Neurosolver for Towers

of Hanoi

For this specific application, there is an opportunity

to apply some modifications to the operation that

diverge from the original intent of Neurosolver.

Again, for this particular application owing to the fact

that the connection weights are ignored, we can just

reverse the search path that led from the goal state to

the current state.

There are two optimizations that we performed

during the search phase that yielded a direct solution;

i.e., the shortest path to the goal.

•

First, let’s observe that since the activity of the

lower divisions of the nodes will spread in the

opposite direction to that of the upper divisions

(since we ignore the probabilities). This means

that every branch of the search tree leads to the

goal if traversed in the opposite direction to the

flow of search. This has the implication that there

are no dead ends; essentially, all branches that do

not lead to the goal, or that are loops, are cut out.

It is clearly seen in Figure 10 that shows that the

solving activity (starting in the start/current node)

cannot go “against the traffic” into any of the

branches.

•

The second optimization is that during the search

phase, we only create directed search connections

if the node has not already been activated in the

progression of the current search. This is

essentially “shutting down” the node during the

search after it conducts the search activity first

time. This follows the observation that if during

the search the node we are trying to move to has

already been activated previously, we must be in

a loop, since the search activity must have been

carried over some other path first. Since that other

path evidently carried the activity faster, the path

that is attempted now must be a longer, less

optimal path; hence, no learning should take

place, so no connection is made. This has the

effect of breaking any loops, since the last

connection is a loop is prevented. Since any loop

Neurosolver Learning to Solve Towers of Hanoi Puzzles

is prevented, each path is a loop-less branch;

hence, it will be effectively pruned by the effects

of the first optimization.

Using the above two optimizations, the only path

from the current state to the goal state is the shortest

optimal path; the best possible solution.

3 CONCLUSIONS

Neurosolver was able to solve Towers of Hanoi

problems without knowing anything specific about

the problem domain. Figure 11 and Figure 12 show

the results of tests in solving problems in three-tower

puzzles with three and with nine disks respectively.

Substantially longer training was required for

building a model for the nine-disc version. It took

1,000,000 steps vs. 10,000 that were sufficient to

create a model for the four disc version. Evidently,

Neurosolver suffers from the similar problem as other

methods that have been tried to solve Towers of

Hanoi puzzle problems: exponential explosion.

However, by not having all possible states in the

system (as the system is prevented from entering

illegal states), the state space is significantly reduced.

That has a positive effect on the efficiency of

searches. The downside of this is that the training

sessions must be sufficiently long to ensure that all

legal states are included in the training (and hence in

the model), since otherwise some problems may not

be solvable, or their solutions might not be optimal.

The approach taken here considers the shortest

path as the best. That may not necessarily be true. Just

like avoiding bad parts of the city while planning

errands some applications may have the quality of

problem solutions evaluated by another measure. One

aspect of such evaluation might be based on the

frequency of state transitions, so the strength of the

connections that Neurosolver accumulates may be

needed. As we said, it’s an unlikely scenario in the

case of Towers of Hanoi, and accordingly we did not

find much use of that capability.

One observation about using the connection

strengths in searches, was that extremely high values

of initial activation were needed to extend the reach

of the search activity from the goal node to the current

node; the more complex the puzzle (more discs), the

higher initial activity was needed. This is because at

every node, the amount of activation is reduced by a

certain percentage depending on the distribution of

This is clearly the area in which an analog implementation

of Neurosolver would be superior. The analog search signal

probabilities amongst the connections. To understand

this, let’s consider the case where all paths are equally

likely, and there are just two outgoing connections

from each node. The “resistance” will be 50% of the

current activation and the projection is split between

the two neighbors. Using this simple observation, we

can see that to move through n consecutive nodes, we

will need an activation value of 2

, as each node will

reduce our activation by 2.

Figure 11: The optimal solution to a problem in a three-

tower four-disc Towers of Hanoi puzzle.

Finding the right activation amount is a problem in

itself: too high value might lead to an infinite search,

as all paths will be activated; too low value may not

spread far enough to reach the current node. In both

cases no solution will be generated. Finding the

minimal value sufficient to find a solution requires an

incremental approach in which the activity is

gradually increased, and that unfortunately leads to

increase in the processing as the whole search must

be redone for the new value

Taking all of these divagations into account, in

the case of this application, we found that ignoring the

connection strengths offered not only the quickest

solutions, but also had the added benefit of

guaranteeing the shortest path; i.e., the optimal

solution for a Towers of Hanoi puzzle.

would be continuously increased until one of the nodes

fires.

States found: 81 out of 81 possible.

Searching...

Start found 15 nodes away, out of 81

states, after checking 80 nodes.

Solving...

1234,0000,0000

0234,0001,0000

0034,0001,0002

0034,0000,0012

0004,0003,0012

0014,0003,0002

0014,0023,0000

0004,0123,0000

0000,0123,0004

0000,0023,0014

0002,0003,0014

0012,0003,0004

0012,0000,0034

0002,0001,0034

0000,0001,0234

0000,0000,1234

Solution Length: 15

Runtime: 0.260015 sec

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications

Figure 12: The optimal solution to a problem in a three-

tower four-disc Towers of Hanoi puzzle. Note that most of

the steps are not shown; only the beginning and the end of

the solution are included.

It was also interesting to observe that the “search”

was simply an encoding of activation data across

Neurosolver itself, without a clear and specific path

being generated. But by using this data, a solution

could be constructed.

For the Tower of Hanoi problem, Neurosolver

worked extremely well. Although this problem did

not take full advantage of Neurosolver capabilities,

through tackling it we did show again that in fact

Neurosolver can solve state-space problems without

having any intrinsic knowledge about the specifics of

the problem domain. That reaffirms our conviction

that Neurosolver indeed is a general problem solver.

4 FUTURE

We are in the process of expanding our experiments

to generalized Towers of Hanoi puzzles like Reve’s

puzzle. In theory, Neurosolver should be able to solve

problems for these puzzles since they also can be

modeled by state spaces.

It is evident that for applications in which

connection strengths are desirable, the issue with

selecting appropriate initial search activity is of

paramount importance. Baring a somewhat elusive

hardware-based analog implementations of

Neurosolver, a good approach could be to set the

activity of each subsequent node to the same activity

at each step of the computation. We are expanding

our model to use activation functions other than the

linear function used in the current implementation

(threshold, sigmoidal, etc.). For this round, we had it

on a back burner, since we did not need to use

probabilities in the experiments with tackling Towers

of Hanoi problems.

While adding front end sensory and back end

effector interfaces would not bring much to the

fundamentals of Neurosolver’s operation, it would

create a more realistic exploratory and demonstration

environment. We are actually applying Neurosolver

in a robot that has a LIDAR scanner as the sensor and

engine-power wheels as the effectors (Bieszczad,

2015). Nevertheless, in the spirit of deep learning we

are also planning to use puzzle images rather than

encoded configurations for training. For that, we will

add an unsupervised configuration classifier as a front

end (e.g., a Support Vector Machine), and use the

classifier’s output as the input to Neurosolver. While

it will necessarily take some time for the classifier to

categorize all puzzle configurations consistently, we

hypothesize that given sufficient time, Neurosolver

will acquire the same level of capabilities as with the

tutoring and random methods. We conjecture that

Neurosolver will need to utilize the probabilities, so

that the inter-nodal connectivity has a chance to

evolve to a stable point after the unavoidable chaos

caused by initial poor input from the classifier.

REFERENCES

Anderson, J. R., 1983. A spreading activation theory of

memory. In Journal of Verbal Learning and Verbal

Behavior, 22, 261-295.

Bieszczad, A. and Pagurek, B., 1998. Neurosolver:

Neuromorphic General Problem Solver. In Information

Sciences: An International Journal 105, pp. 239-277,

Elsevier North-Holland, New York, NY.

Bieszczad, A., 2008. Exploring Neurosolver’s Forecasting

Capabilities. In Proceedings of the 28th International

Symposium on Forecasting, Nice, France, June 22-25.

Bieszczad A., (2011). Predicting NN5 Time Series with

Neurosolver. In Madani, K., Correia, A., Rosa, A., and

Filipe, J. (Eds.), Computational Intelligence: Revised

and Selected Papers of the International Joint

Conference IJCCI 2009 held in Funchal-Madeira,

Portugal, October 2009 (Studies in Computational

Intelligence). Berlin Heidelberg: Springer-Verlag, pp.

277-288.

Bieszczad, A. and Bieszczad, K., (2007) Running Rats with

Neurosolver-based Brains in Mazes. In Journal of

States found: 19683 out of 19683

possible.

Searching...

Start found 511 nodes away, out of

19683 states, after checking 19207

nodes.

Solving...

123456789,000000000,000000000

023456789,000000000,000000001

003456789,000000002,000000001

003456789,000000012,000000000

000456789,000000012,000000003

001456789,000000002,000000003

001456789,000000000,000000023

000456789,000000000,000000123

…

000000023,000000000,001456789

000000003,000000002,001456789

000000003,000000012,000456789

000000000,000000012,003456789

000000001,000000002,003456789

000000001,000000000,023456789

000000000,000000000,123456789

Solution Length: 511

Runtime: 135.752254 sec

Neurosolver Learning to Solve Towers of Hanoi Puzzles

Information Technology and Intelligent Computing,

Vol. 1 No. 3.

Bieszczad, A. and Bieszczad, K., (2006). Contextual

Learning in Neurosolver. In Lecture Notes in Computer

Science: Artificial Neural Networks, Springer-Verlag,

Berlin, 2006, pp. 474-484.

Burnod, Y., 1988. An Adaptive Neural Network: The

Cerebral Cortex, Paris, France: Masson.

Collins, Allan M.; Loftus, Elizabeth F., 1975. A Spreading-

Activation Theory of Semantic Processing. In

Psychological Review. Vol 82(6) 407-428.

Deutsch, M., 1960. The Effect of Motivational Orientation

Upon Trust And Suspicion. In Human Relations, 13:

123–139.

Laird, J. E., Newell, A. and Rosenbloom, P. S., 1987.

SOAR: An architecture for General Intelligence. In

Artificial Intelligence, 33: 1--64.

Markov, A. A., 2006. An Example of Statistical

Investigation of the Text Eugene Onegin Concerning

the Connection of Samples in Chains (translation. by

David Link). In Science in Context 19.4: 591-600.

Newell, A. and Simon, H. A., 1963. GPS: A program that

simulates human thought. In Feigenbaum, E. A. and

Feldman, J. (Eds.), Computer and Thought. New York,

NJ: McGrawHill.

Nillson, N. J., 1980. Principles of Artificial Intelligence,

Palo Alto, CA: Tioga Publishing Company.

Russell, Stuart J.; Norvig, Peter (2003), Artificial

Intelligence: A Modern Approach (2nd ed.). Upper

Saddle River, NJ: Prentice Hall, pp. 111-114.

Stewart, B. M. and Frame, J. S., 1941. Solution to Advanced

Problem 3819. In The American Mathematical

Monthly Vol. 48, No. 3 (Mar., 1941), pp. 216-219.

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications