Mining Signiﬁcant Frequent Patterns in Parallel Episodes with a Graded

Notion of Synchrony and Selective Participation

Salatiel Ezennaya-Gomez

1,2

and Christian Borgelt

Intelligent Data Analysis Research Unit, European Centre for Soft Computing, c/ Gonzalo Guti

errez Quir

os s/n,

33600 Mieres (Asturias), Spain

Department of Knowledge and Language Processing, Otto-von-Guericke University, Magdeburg, Germany

Keywords:

Graded Synchrony, Synchronous Events, Temporal Imprecision, Selective Participation, Frequent Pattern

Mining.

Abstract:

We consider the task of ﬁnding frequent parallel episodes in parallel point processes (or event sequences),

allowing for imprecise synchrony of the events constituting occurrences (temporal imprecision) as well as

incomplete occurrences (selective participation). The temporal imprecision problem is tackled by frequent

pattern mining using a graded notion of synchrony that captures both the number of instances of a pattern as

well as the precision of synchrony of its events. To cope with selective participation, a reduction sequence of

items (or event types) is formed based on found frequent patterns and guided by pattern overlap. We evaluate

the performance of this method on a large number of data sets with injected parallel episodes. We demonstrate

that, in contrast to binary synchrony where it pays to consider the pattern instances, graded synchrony performs

better with a pattern-based scheme than with an instance-based one, thus simplifying the procedure.

1 INTRODUCTION

We present elaborate methodology to identify mean-

ingful frequent synchronous patterns in event se-

quences (see e.g. (Mannila et al., 1997)), using the

principles of frequent item set mining (FIM) (see

e.g. (Borgelt, 2012)). As is well known, the objec-

tive of FIM is to ﬁnd all item sets that are frequent in

a transaction database. FIM uses the support (number

of occurrences in the transactions) to deﬁne an item

set as frequent, namely if its support reaches or ex-

ceeds a (user-speciﬁed) minimum support threshold.

In standard FIM the support of an item set is a simple

count of transactions, whereas in our case the event

sequence data is continuous in nature, since it resides

in the time domain, and thus no (natural) transactions

exist. This continuous form causes several problems,

especially w.r.t. the deﬁnition of a support measure.

Frequent pattern mining in continuous time faces

two main problems: temporal imprecision and selec-

tive participation. The former is related to the syn-

chrony of events which is affected by temporal jit-

ter, due to which the events are usually not perfectly

aligned. In frequent pattern mining we tackle tem-

poral imprecision by deﬁning that items (or events)

co-occur if they occur in a (user-speciﬁed) limited

time span from each other. In earlier work the

size of a maximum independent set (MIS) of such

synchronous groups of items, which can be com-

puted efﬁciently with a greedy algorithm (see (Borgelt

and Picado-Muino, 2013) and (Picado-Muino and

Borgelt, 2014)), is used as a support measure.

This method is referred to as binary synchrony in

(Ezennaya-G

omez and Borgelt, 2015), because it al-

lows only for two values: either a group of events is

synchronous, or it is not.

Unfortunately, a greedy algorithm no longer guar-

antees an optimal solution when a graded notion of

synchrony is introduced, while a backtracking ap-

proach (as it would be used for a general maximum in-

dependent set problem, which is NP-complete) takes

exponential time in the worst case. As a consequence,

an adaptation is necessary, which takes the form of

an approximation procedure to compute the support,

but maintaining the crucial property of support being

anti-monotone. To this end, (Ezennaya-G

omez and

Borgelt, 2015) deﬁned a graded synchrony approach

where the support computation takes the precision of

synchrony into account. That is, a pattern that has

fewer occurrences, but in each of these the items oc-

cur very closely together in time, is rated better than

an item set, which has more instances, but in each

Ezennaya-Gomez, S. and Borgelt, C..

Mining Signiﬁcant Frequent Patterns in Parallel Episodes with a Graded Notion of Synchrony and Selective Participation.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 3: NCTA, pages 39-48

ISBN: 978-989-758-157-1

of these the synchrony of the events is rather loose

(Ezennaya-G

omez and Borgelt, 2015).

The second problem, that is, selective participa-

tion, is related to the lack of occurrence of some

items, which produces incomplete pattern instances.

As a consequence, only subsets of the actual pattern

are present in the instances underlying a pattern. This

can be caused by imperfections of the measuring tech-

nology or by properties of the underlying process.

(Borgelt et al., 2015) presented an approach to solve

this problem in the binary synchrony setting we men-

tioned above. The goal of this paper is to transfer

this approach from the binary synchrony setting to a

graded synchrony setting, and to investigate whether

the same conclusions can be drawn about the different

variants considered in (Borgelt et al., 2015).

The application area that motivates our work is the

analysis of parallel spike trains in neurobiology. Such

spike trains are sequences of points in time, one per

neuron, that represent the times at which an electrical

impulse (action potential or spike) is emitted. The ob-

jective is to identify cell assemblies or groups of neu-

rons that tend to exhibit synchronous spiking. Such

cell assemblies were proposed in (Hebb, 1949) as a

model for encoding and processing information in bi-

ological neural networks. Since synchronous spike

input to receiving neurons is known to be more effec-

tive in generating output spikes (Abeles, 1982; K

onig

et al., 1996), such cell assemblies are a plausible hy-

pothesis for neural information processing.

The objective of this paper is to adapt the se-

lective participation approach in an algorithm called

CoCoNAD (for Continuous-time Closed Neuron

Assembly Detection, a name inspired by the men-

tioned application domain) to detect signiﬁcant syn-

chronous patterns with a graded notion of synchrony.

As a ﬁrst step to identify of neuronal assemblies,

we look for frequent neuronal patterns (i.e. groups of

neurons that exhibit frequent synchronous spiking). In

this setting, both temporal imprecision and selective

participation are expected to be present and thus re-

quire proper treatment. Once frequent patterns are

detected, additional ﬁltering is necessary to remove

those frequent patterns that are produced by chance

events and thus are not relevant. Then, detection of

selective participation is applied. Due to the graded

nature of the synchrony deﬁnition we adopt, the selec-

tive participation approach needs to be modiﬁed from

the approach presented in (Borgelt et al., 2015).

The remainder of this paper is structured as fol-

lows: Section 2 covers basic terminology and nota-

tion and introduces our graded notion of synchrony.

In Sections 3 and 4 we show how a support based on

graded synchrony is approximated and frequent syn-

chronous patterns are mined and ﬁltered using pat-

tern spectrum ﬁltering. In Section 5 we present our

methodology to identify frequent parallel episodes

with selective participation with a graded notion of

synchrony. Section 6 reports experimental results on

data sets with injected parallel episodes. Finally, in

Section 6 we draw conclusions from our discussion.

2 EVENT SEQUENCES &

SYNCHRONY

We adopt notation and terminology from (Mannila

et al., 1997) and (Ezennaya-G

omez and Borgelt,

2015). The data are sequences of events S =

{hi

i, . . . , hi

i}, m ∈ N, where i

in the event

i is the event type or item (taken from an

item base B) and t

∈ R is the time of occurrence

of i

, k ∈ {1, . . . , m}. Note that the fact that S

is a set implies that there cannot be two events

with the same item occurring at the same time:

events with the same item must differ in their oc-

currence time and events occurring at the same time

must have different types/items. Such data may

as well be represented as parallel point processes

P = {hi

, {t

(1)

, . . . , t

(1)

}i, . . . , hi

, {t

(n)

, . . . , t

(n)

}i} by

grouping events with the same item i ∈ B, n = |B|,

and listing the times of their occurrences for each of

them. Finally, note that in our motivating application

(i.e. spike train analysis), the items (or event types)

are the neurons and the corresponding point processes

list the times at which spikes were recorded for these

neurons (Ezennaya-G

omez and Borgelt, 2015).

A synchronous pattern (in S) is deﬁned as a set of

items I ⊆ B that occur several times (approximately)

synchronously in S. Formally, an instance (or occur-

rence) of such a synchronous pattern (or a set of syn-

chronous events for I) in an event sequence S with re-

spect to a user-speciﬁed time span w ∈ R

is deﬁned

as a subsequence R ⊆ S , which contains exactly one

event per item i ∈ I and which can be covered by a

time window at most w wide. Let φ the pattern op-

erator that yields the pattern underlying an instance,

φ(R ) = {i | hi, ti ∈ R }. Hence the set of all instances

of a pattern I ⊆ B, I 6=

0, in an event sequence S is

S,w

(I) =



R ⊆ S | φ(R ) = I

∧ |R | = |I| ∧ σ

(R ) > 0



where σ

is the synchrony operator which measures

the degree of synchrony of the events in R .

The synchrony operator should conincide with bi-

nary synchrony for limiting cases as follows: if all

events in R coincide (i.e. have exactly the same oc-

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications

(R)

d(R)

d(R) = max

hi,ti∈R

− min

hi,ti∈R

perfect

synchrony

Figure 1: Degree of synchrony as a function of the distance

between the latest and the earliest event.

currence time, perfect synchrony), the degree of syn-

chrony should be 1, while it should be 0 if the events

are spread out farther than the window width w (no

synchrony). However, if the (time) distance between

the earliest and the latest event in R is between 0

and w, we want a degree of synchrony between 0

and 1.

Such a synchrony operator was described in

(Picado-Muino et al., 2012) based on the notion of

an inﬂuence map, which is placed at each event and

describes the vicinity around an event in which syn-

chrony with other events is deﬁned. Such an inﬂuence

map for an event occurring at time t is deﬁned as a

function

(x) =



if x ∈ [t −

,t +

0 otherwise.

Based on inﬂuence maps, events are synchronous

iff their inﬂuence maps overlap. The area of the over-

lap measures the degree of synchrony (Figure 1):

(R ) =

∞

min

hi,ti∈R

(x, w) dx.

Alternatively, we may use the equivalent deﬁnition

(R ) = max

0, 1 −



max

hi,ti∈R

t − min

hi,ti∈R

o

The synchrony operator underlies the deﬁnition of

a support operator s

S,w

(I) that is used to mine syn-

chronous patterns. The support should capture (also)

the number of occurrences of a pattern in a given

event sequence S. In addition, in order to be efﬁ-

cient, frequent pattern mining requires support to be

anti-monotone: ∀I ⊆ J ⊆ B : s

S,w

(I) ≥ s

S,w

(J). Or

in words: if an item is added to an item set, its sup-

port cannot increase. This implies the so-called apri-

ori property: ∀I, J ⊆ B : (J ⊇ I ∧ s

S,w

(I) < s

min

) ⇒

S,w

(J) < s

min

. Or in words: no superset of an infre-

quent pattern can be frequent. The apriori property

allows to prune the search for frequent patterns effec-

tively (Borgelt, 2012).

Given a support measure and a (user-speciﬁed)

minimum support s

min

, the task of frequent syn-

chronous pattern mining is deﬁned as the task to iden-

tify all item sets I ⊆ B with s

S,w

(I) ≥ s

min

((Borgelt,

2012)).

t (time)

Intersection

of inﬂuence

maps

neurons

union of

inﬂuence

maps

Figure 2: Support computation for three items a, b, c. Each

event has its inﬂuence map (represented as a rectangle). If

two inﬂuence maps overlap, the resulting inﬂuence map is

the maximum (union) of these inﬂuence maps. The inter-

section of inﬂuence maps is the minimum which deﬁnes the

synchrony operator. In the diagram, item b has two events

the inﬂuence regions of which overlap. The support results

from the integral over the intersections.

3 SUPPORT COMPUTATION FOR

GRADED SYNCHRONY

For binary synchrony the support is computed efﬁ-

ciently using a greedy algorithm. However, following

(Ezennaya-G

omez and Borgelt, 2015) and as we men-

tioned in the introduction, for graded synchrony such

an approach does not guarantee an optimal result and

thus needs to be replaced by an approximation.

As such an approximation, deﬁned in (Ezennaya-

omez and Borgelt, 2015), the integral over the max-

imum (union) of the minimum (intersection) of inﬂu-

ence regions is chosen: the minimum represents the

synchrony operator, the maximum takes care of a pos-

sible overlap between instances of synchronous event

groups, and the integral ﬁnally aggregates over differ-

ent instances. Formally:

S,w

(I) =

∞

−∞

max

R ∈E

S,w

(I)



min

hi,ti∈R

(x)



dx.

The advantages of this support measure are mainly

two: in the ﬁrst place, the support measure deﬁned in

this way is anti-monotone due to the minimum over

i ∈ I. Secondly, it allows to compute the support by a

simple intersection of interval lists, since all occurring

functions only take two values, namely 0 and

, and

therefore it sufﬁces to record where they are greater

than 0. Thus, the list of intervals for each item i ∈ B

in which max

h j,ti∈S; j=i

(x) > 0 is computed. These

intervals can then be intersected to account for the

minimum. Summing the interval lengths and divid-

ing by w we obtain the area under the functions (see

the example described in Figure 2).

Mining Signiﬁcant Frequent Patterns in Parallel Episodes with a Graded Notion of Synchrony and Selective Participation

Note that this computation scheme is very simi-

lar to the Eclat algorithm (Zaki et al., 1997) (which

works by intersecting transaction identiﬁer lists),

transferred to a continuous domain (and thus to ef-

fectively inﬁnitely many transactions). As a conse-

quence, Eclat’s item set enumeration scheme, which

is based on a simple divide-and-conquer approach,

can be applied with only few adaptations (concerning

mainly the support computation) to obtain an efﬁcient

algorithm for mining frequent synchronous patterns

(see e.g. (Borgelt, 2012)).

4 PATTERN SPECTRUM

FILTERING

The large number of patterns in the output of syn-

chronous pattern mining method is a problem and

thus further reduction is necessary. This is done by

identifying statistically signiﬁcant patterns. Previ-

ous work showed that statistical tests on individual

patterns are not suitable (Picado-Muino et al., 2013;

Torre et al., 2013). The main problems are the lack of

proper test statistics as well as multiple testing, that is,

the huge number of patterns makes it very difﬁcult to

control the family-wise error rate, even with control

methods like Bonferroni correction, the Benjamini-

Hochberg procedure or the false discovery rate etc.

(Dudoit and van der Laan, 2008).

To overcome this problem, we rely here on the ap-

proach suggested in (Picado-Muino et al., 2013) and

reﬁned in (Torre et al., 2013), namely Pattern Spec-

trum Filtering (PSF). This method is based on the fol-

lowing insight: even if it is highly unlikely that a spe-

ciﬁc group of z items co-occurs s times, it may still be

likely that some group of z items co-occurs s times,

even if items occur independently. From this insight

it was derived in (Picado-Muino et al., 2013) that pat-

terns should rather be judged based on their signa-

ture hz, si, where z = |I| is the size of a pattern I and s

its support. A pattern is not signiﬁcant if a counterpart

which has the same or larger pattern size z and same

or higher support s can be explained as a chance event

under the null hypothesis of independent events.

In order to determine the likelihood of observing

different pattern signatures hz, si under the null hy-

pothesis of independent items, a data randomization

or surrogate data approach is employed. The general

idea is to represent the null hypothesis implicitly by

(surrogate) data sets that are generated from the orig-

inal data in such a way that their occurrence probabil-

ity is (approximately) equal to their occurrence prob-

ability under the null hypothesis. Such an approach

has the advantage that it needs no explicit data model

support

pattern

size

log(#patterns)

–4

–3

–2

–1

pattern

spectrum

Figure 3: Pattern spectrum generated from 10

surrogate

data sets.

for the null hypothesis, which in many cases (includ-

ing the one we are dealing with here) may be difﬁcult

to specify. Instead, the original data is modiﬁed in

random ways to obtain data that are at least analo-

gous to those that could be sampled under conditions

in which the null hypothesis holds. An overview of

several surrogate data methods in the context of neu-

ral spike train analysis can be found in (Louis et al.,

2010).

Summarizing, the objective of PSF is to pool the

resulting patterns from the output of synchronous pat-

tern mining with the same or larger signature hz, si

ﬁltering by the surrogate data sets generated as an im-

plicit representation of the null hypothesis. An exam-

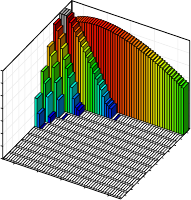
ple of such a pattern spectrum, for data as it will be

used in Section 6, is shown in Figure 3. It captures

what pattern signatures occurred in a large number of

surrogate data sets. Note that since we are working in

continuous time domain the support values are (non-

negative) real numbers.

5 SELECTIVE PARTICIPATION

METHOD

To achieve the purpose of this paper we draw in the

same idea described in (Borgelt et al., 2015) to iden-

tify parallel episodes in the presence of selective par-

ticipation. The approach is based on the following

insight: although incomplete occurrences of a pat-

tern may make it impossible that the full pattern is

reported by the mining procedure, it is highly likely

that several overlapping subsets will be reported. An

example of this situation is illustrated in Figure 4,

which shows parallel spike trains of six neurons a to f

with complete and incomplete instances of the paral-

lel episode comprising all six neurons (in blue; while

background spikes are shown in gray). Although the

full set of neurons ﬁres together only once (leftmost

instance) and thus would not be detected, the other

ﬁve incomplete occurrences give rise to ﬁve subsets

of size 4, each of which occurs twice, and many sub-

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications

Figure 4: Parallel episodes (indicating neuron assembly ac-

tivity) with selective participation (blue) as well as back-

ground spikes (gray).

sets of size 3, occurring 3 or more times. Since these

patterns overlap heavily, it should be possible to re-

construct the full pattern by analyzing pattern overlap

and combining patterns.

The method views the set of patterns that were

found in a given data set as a hypergraph

on the

set of items (which are the vertices of this hyper-

graph): each pattern forms a hyperedge. Patterns that

are affected by selective participation thus give rise

to densely connected sub-hypergraphs. Hence, we

should be able to identify such patterns by ﬁnding

densely connected sub-hypergraphs, (Borgelt et al.,

2015).

The method draws on the approach proposed in

(Tsourakakis et al., 2013) for detecting dense sub-

hypergraphs. Although this approach was designed

to ﬁnd dense subgraphs in standard graphs, its ba-

sic idea is easily transferred and adapted: we form

a reduction sequence of items by removing, in each

step, the item that is least connected to the other items

(that are still considered). Then we identify from this

sequence the set of items where the least connected

item (i.e., the one that was removed next) was most

strongly connected (compared to other steps of the se-

quence). This item set is the result of the procedure,

(Borgelt et al., 2015).

Although this limits the basic procedure to the

identiﬁcation of a single pattern, it is clear that multi-

ple patterns can easily be found with the same amend-

ment as suggested in (Tsourakakis et al., 2013): ﬁnd

a pattern and then remove the underlying items (ver-

tices) from the data. Repeat the procedure on the re-

maining items to ﬁnd a second pattern. Remove the

items of this second pattern and so on. A drawback

of this approach is that it can ﬁnd only disjoint pat-

terns and thus fails to identify overlapping patterns.

However, given the general difﬁculty to handle selec-

tive participation, we believe that this is an acceptable

shortcoming.

Formally, a reduction sequence of item sets is con-

structed, starting from the item base B, as

While in a standard graph any edge connects exactly

two vertices, in a hypergraph a single hyperedge can con-

nect arbitrarily many vertices.

= B, where n = |B|,

= J

k+1

− {argmin

i∈J

k+1

S,w,s

min

(i, J

k+1

)},

for k = n − 1, n − 2, . . . , 0,

where ξ

S,w,s

min

(i, J

) denotes the strength of connec-

tion that item i ∈ J

has to the other items in the

set J

, as it is induced by the (closed) frequent pat-

terns found when mining the sequence S with window

width w and minimum support s

min

(concrete func-

tions ξ

S,w,s

min

(i, J

) are studied below). Then, we as-

sign a quality measure to each element of this reduc-

tion sequence:

∀k; 0 ≤ k ≤ n :

S,w,s

min

) = min

i∈J

S,w,s

min

(i, J

Finally, we select the pattern (item set)

I = argmax

;0≤k≤n

S,w,s

min

that is, the pattern with the highest quality (sub-

hypergraph density), as the result of our procedure.

To obtain concrete instances of the functions

S,w,s

min

(i, J

), two different approaches were deﬁned

in (Borgelt et al., 2015): a pattern-based approach

which works with patterns and support and instance-

based approach which tries to remove instances to

focus the evaluation on instances that likely resulted

from the actual assembly activity. These methods are

described for binary synchrony. To apply them to

our graded synchrony, a re-deﬁnition of the latter was

necessary and it is described further down.

Pattern-based Approach

Let C

∗

(w, s

min

) ⊆ 2

be the set of closed frequent pat-

terns that are identiﬁed by the CoCoNAD algorithm

with a graded notion of synchrony (if executed with

window width w and minimum support s

min

on S),

for which no counterpart (no signature with the same

size and greater or equal support constitutes a coun-

terpart) was observed in any of the surrogate data sets

(that is, the closed frequent patterns remaining after

pattern spectrum ﬁltering). Let C

∗

S,J

(w, s

min

) = {I ∈

∗

(w, s

min

) | I ⊆ J} be the subset of these patterns that

are subsets of an item set J. Then we deﬁne the hy-

pergraph connection strength of item i ∈ J to the other

items in J as

(pat)

S,w,s

min

(i, J) =

∑

I∈C

∗

S,J

(w,s

min

)

(|I| − r) · s

S,w

(I),

where r ∈ {0, 1} is a parameter that determines

whether the full pattern size (hyperedge size) should

be considered (r = 0), or whether the item i itself

should be disregarded (r = 1). The support of the

item set I enters the deﬁnition because a larger sup-

port clearly means a stronger connection.

Mining Signiﬁcant Frequent Patterns in Parallel Episodes with a Graded Notion of Synchrony and Selective Participation

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

i 0

Figure 5: Experimental results with ν = 1 (each item missing from one instance). Patterns ﬁltered by 10, 100, and 1000

surrogate data sets.

Intuitively, ξ

(pat)

S,w,s

min

(i, J) sums the grades of syn-

chrony underlying each of the patterns that connect i

to the other items in J.

Note that in this deﬁnition we assume (as is com-

mon practice) that ξ

(pat)

S,w,s

min

(i, J) = 0 if C

∗

S,J

(w, s

min

) =

This approach has the advantage that merely the

ﬁltered set of closed frequent patterns is needed.

However, it has the disadvantage that subset patterns

which, by chance, occur again outside of the instances

of the full pattern may deteriorate the detection qual-

ity. An example of such an occurrence can be seen

in Figure 4: the neurons a, b and e ﬁre together be-

tween the second and third instance of the full set.

However, this is not an incomplete instance of the full

set, but rather a chance coincidence resulting from

the background spikes. This can lead to a subset be-

ing preferred to the full pattern, even though the sum

in the above deﬁnition gives higher weight to events

that support multiple instances (as these are counted

multiple times). Removing instances is necessary to

improve the detection quality. To obtain concrete in-

stances of the functions ξ

S,w,s

min

(i, J

) we deﬁne:

Instance-based Approach

We start from the same idea in (Borgelt et al., 2015)

that we only want to consider instances that are not

“isolated”, but “overlap” some other instance (prefer-

ably of a different pattern). The reason is that iso-

lated instances likely stem from chance coincidences,

while instances that “overlap” other instances likely

stem from the same (complete or incomplete) in-

stance of the full pattern we try to identify. Unlike

(Borgelt et al., 2015) where the instance-based ap-

proach merely counts spikes without considering the

precision of synchrony, in our approach we recompute

the support from the reduced set of instances, which

is simple as the instances are known.

Let C

∗

(w, s

min

) and C

S,J

(w, s

min

) be deﬁned as

above. Let U

S,w

(I) ⊆ E

S,w

(I) be the set of all in-

stances of I that was identiﬁed by the CoCoNAD al-

gorithm in order to compute the support s

S,w

(I). Fur-

thermore, let V

S,w,s

min

(J) =

I∈C

∗

S,J

(w,s

min

)

S,w

(I).

That is, V

S,w,s

min

(J) is the set of all instances underly-

ing all patterns found in S that are subsets of J.

To implement our idea of keeping overlapping in-

stances of different patterns, we deﬁne

∗

S,w,s

min

(i, J) =

{R ∈ V

S,w,s

min

(J) | ∧ ∃T ∈ V

S,w,s

min

(J):

φ(T ) 6= φ(R ) ∧ o

(T , R ) = 1},

where φ is the pattern operator deﬁned in Section 2

and o

(R , T ) is an operator that tests whether the in-

stances R and T overlap. In words: V

∗

S,w,s

min

(i, J)

is the set of instances of patterns that contain the

item i ∈ J and are subsets of the set J, which over-

lap at least one other instance of a different pattern.

The operator o

checks whether the instances have a

non-empty intersection. The instance-based approach

has the advantage that chance coincidences are much

less likely to deteriorate the detection quality. How-

ever, its disadvantage is that it is more costly to com-

pute, because not just the patterns, but the individual

instances of all relevant patterns have to be processed.

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications

time

neurons

Figure 6: Example of generated data sets that imitate par-

allel neural spike trains. Each row of blue dots represents

the spike train of each neuron. In this example the injected

patterns are drawn in red.

The selective participation adaptation method pro-

poses to study only instances that overlap with other

instances of different patterns, re-compute the support

for these patterns and ﬁnally apply the pattern-based

approach.

6 EXPERIMENTS

We implemented our frequent synchronous pattern

mining method in Python, using an efﬁcient C-based

Python extension module that implements the pat-

tern mining and surrogate generation.

We gener-

ated event sequence data as independent Poisson pro-

cesses with parameters chosen in reference to our ap-

plication domain: 100 items (number of neurons that

can be simultaneously recorded with current technol-

ogy), 20Hz event rates (typical average ﬁring rate ob-

served in spike train recordings), 3s total time (typical

recording times for spike trains range from a few sec-

onds up to about an hour).

Into such independent data sets we injected a sin-

gle synchronous pattern each, with sizes z ranging

from 2 to 12 items and numbers c of occurrences (in-

stances) ranging from 2 to 12. To simulate imprecise

synchrony, the events of each pattern instance were

jittered independently by drawing an offset from a

uniform distribution on [−1ms, +1ms] (which corre-

The implementation of the CoCoNAD algorithm is de-

veloped in Python (Rossum, 1993) and the core of the al-

gorithm is developed in C (Kernighan and Ritchie, 1978).

This implementation can be found at

http://www.borgelt.net/coconad.html and

http://www.borgelt.net/pycoco.html.

A Java graphical user interface is available at

http://www.borgelt.net/cocogui.html.

The scripts with which we executed our experiments as well

as the complete result diagrams (all parameter combina-

tions) will be available at

http://www.borgelt.net/hypernad.html.

sponds to typical bin lengths for time-binning of par-

allel neural spike trains, which are 1 to 7ms). An ex-

ample of such a data set is depicted in Figure 6.

To simulate selective participation, we deleted

each item of a parallel episode from a number ν ∈

{1, 2, 3, 4, 5} of their instances. This created data sets

with instances similar to those shown in Figure 4

(which corresponds to z = 6, c = 6 and ν = 1, but

has much fewer background spikes): a few instances

may be complete, but most lack a varying number of

items. For each signature hz, ci of a parallel episode

and each value of ν we created 1000 such data sets.

Then we tried to detect the injected synchronous

patterns with the methods described in Sections 4 and

5. For mining closed frequent patterns we used dif-

ferent values of the window width, w ∈ {2, 3, 4, 5}

(matching the jitter of the temporal imprecision) us-

ing a minimum support s

min

= 1.0 and a minimum

pattern size z

min

= 2. Based on results presented in

(Ezennaya-G

omez and Borgelt, 2015), the window

value used is

j. Then ﬁltering patterns mined with

different pattern spectrum derived from 10, 100 and

1000 data sets with independent spike trains. The

method described in Section 5 is applied to the re-

sulting patterns.

Some of the results we obtained are depicted in

Figures 5, 7, and 8. In each row of the ﬁgures, the

ﬁrst diagram shows the number of (strict) false nega-

tives, that is, the fraction of runs (of 1000) in which

something else than exactly the injected pattern was

found. In order to elucidate what happens in those

runs in which the injected parallel episode was not

(exactly) detected, the diagrams in columns 2 and 3

show the fraction of runs in which a superset or a sub-

set, respectively, of the injected parallel episode was

returned. Column 4 shows the fraction of runs with

overlap patterns (the reported pattern contains some,

but not all of the items of the injected parallel episode

and at least one other item), column 5 the fraction of

runs with patterns that are unrelated to the injected

parallel episode. On top of each diagram the different

approaches are shown with its parameters. The ﬁrst

value corresponds to the number of missing instances

followed by the type of ﬁlter, and the type of reduction

sequence approach applied and value of r parameter.

Figure 5 shows the different results obtained by

ﬁltering closed frequent patterns with the different

patterns spectra (10, 100 and 1000). Note that graded

synchrony has less problems with unrelated patterns.

We observe that ﬁltering by surrogates derived from

100 and 1000 performs better w.r.t. unrelated patterns.

That is, ﬁltering with 100 and 1000 surrogate data sets

detect every injected pattern if only something is de-

tected at all. Figure 7 shows a comparison between

Mining Signiﬁcant Frequent Patterns in Parallel Episodes with a Graded Notion of Synchrony and Selective Participation

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

i 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

i 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

i 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

i 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

i 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

p 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

p 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

p 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

p 1

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

p 1

Figure 7: Experimental results with instance-based approach and pattern-based approach for graded synchrony (each item

missing from one instance).

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

p 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

false neg.

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

supersets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

subsets

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

overlap

1 10

i 0

pattern

size

instances

rate

0.2

0.4

0.6

0.8

unrelated

1 10

i 0

Figure 8: Comparison between the instance/pattern-based approach for graded synchrony and the instance-based approach

for binary synchrony.

the instance-based approach and the pattern-based ap-

proach using graded synchrony. The ﬁrsts two rows

of diagrams show results for r = 0 and the second

two rows correspond to r = 1. The pattern-based ap-

proach is slightly better than the instance-based ap-

proach in terms of false negatives (exact pattern de-

tection). Concretely, for r = 1, the pattern-based ap-

proach has better ratios in supersets and overlaps by

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications

paying a price of a slightly worse ratio for subsets.

Taken together, the price of having more subsets is

preferred, because subsets contain only items actually

in the assembly, while superset and overlap patterns

also contain unrelated items.

The ﬁrst and second row of ﬁgure 8 correspond

to the instance and the pattern-based approach for

graded synchrony. The third corresponds to the

instance-based approach for binary synchrony. Com-

paring the diagrams for unrelated patterns, our graded

method detects all injected patterns (ﬁrst and sec-

ond rows), while the binary method also produces

unrelated pattern. In (Borgelt et al., 2015) it is

demonstrated that the instance-based approach yields

slightly better results than the pattern approach. How-

ever, this approach does not consider the precision of

synchrony. Surprisingly, using only the pattern-based

approach with a graded notion of synchrony yields a

better ratio for overlap and superset patterns.

7 CONCLUSIONS

In this paper we presented a method to detect fre-

quent synchronous patterns in event sequences using

a graded notion of synchrony for mining patterns in

the presence of imprecise synchrony of events con-

stituting occurrences and selective participation (in-

complete occurrences). Our method adapts methods

presented in the literature to tackle selective participa-

tion using binary synchrony, especially the instance-

based approach which looks at instances of patterns to

improve the detection by removing instances that are

likely chance events, checking the precision of syn-

chrony of these instances. We demonstrate in our ex-

periments that using a graded notion of synchrony for

support computation helps to simplify the detection

of selective participation, because a pattern-based ap-

proach yields better results or at least equally good

results as an instance-based approach. This is a con-

siderable advantage, since identifying the individual

pattern instances is costly and thus it is desirable to

avoid it.

ACKNOWLEDGMENTS

The work presented in this paper was partially sup-

ported by the Spanish Ministry for Economy and

Competitiveness (MINECO Grant TIN2012-31372)

and by the Principality of Asturias, through the

2013-2017 Science Technology and Innovation Plan

(Programa Asturias, CT1405206), and the European

Union, through FEDER funds.

REFERENCES

Abeles, M. (1982). Role of the cortical neuron: Integrator

or coincidence detector? Israel Journal of Medical

Sciences, 18(1):83–92.

Borgelt, C. (2012). Frequent item set mining. In Wiley

Interdisciplinary Reviews (WIREs): Data Mining and

Knowledge Discovery, pages 437–456. ( J. Wiley &

Sons, Chichester, United Kingdom, 2.

Borgelt, C., Braune, C., and Loewe, K. (2015). Mining fre-

quent parallel episodes with selective participation. In

Proc. 16th World Congress of the International Fuzzy

Systems Association (IFSA) and 9th Conference of

the European Society for Fuzzy Logic and Technol-

ogy (EUSFLAT), IFSA-EUSFLAT2015, Gijon, Spain.

Atlantis Press.

Borgelt, C. and Picado-Muino, D. (2013). Finding fre-

quent synchronous events in parallel point processes.

In Proc. 12th Int. Symposium on Intelligent Data

Analysis (IDA 2013, London, UK), pages 116–126,

Berlin/Heidelberg, Germany. Springer-Verlag.

Dudoit, S. and van der Laan, M. J. (2008). Multiple Testing

Procedures with Application to Genomics. Springer,

New York, USA.

Ezennaya-G

omez, S. and Borgelt, C. (2015). Mining fre-

quent synchronous patterns with a graded notion of

synchrony. In Proc. 16th World Congress of the In-

ternational Fuzzy Systems Association (IFSA) and 9th

Conference of the European Society for Fuzzy Logic

and Technology (EUSFLAT), IFSA-EUSFLAT2015,

pages 1338–1345, Gijon, Spain. Atlantis Press, ISBN

(on-line): 978-94-62520-77-6.

Hebb, D. O. (1949). The Organization of Behavior. J. Wiley

& Sons, New York, NY, USA.

Kernighan, W. and Ritchie, D. (1978). The C Programming

Language. Prentice Hall.

onig, P., Engel, A. K., and Singer, W. (1996). Integrator or

coincidence detector? the role of the cortical neuron

revisited. Trends in Neurosciences, 19(4):130–137.

Louis, S., Borgelt, C., and Gr

un, S. (2010). Generation and

selection of surrogate methods for correlation analy-

sis. In Gr

un, S. and Rotter, S., editors, Analysis of Par-

allel Spike Trains, pages 359–382. Springer-Verlag,

Berlin, Germany.

Mannila, H., Toivonen, H., and Verkamo, A. (1997). Dis-

covery of frequent episodes in event sequences. In

Data Mining and Knowledge Discovery, pages 259–

289. Springer, New York, NY, USA, 1(3).

Picado-Muino, D. and Borgelt, C. (2014). Frequent item-

set mining for sequential data: Synchrony in neuronal

spike trains. Intelligent Data Analysis, 18(6):997–

1012.

Picado-Muino, D., Borgelt, C., Berger, D., Gerstein, G. L.,

and Gr

un, S. (2013). Finding neural assemblies with

frequent item set mining. Frontiers in Neuroinformat-

ics, 7.

Picado-Muino, D., Castro-Le

on, I., and Borgelt, C. (2012).

Fuzzy frequent pattern mining in spike trains. In

Proc. 11th Int. Symposium on Intelligent Data Anal-

ysis (IDA 2012, Helsinki, Finland), pages 289–300,

Berlin/Heidelberg, Germany. Springer-Verlag.

Mining Signiﬁcant Frequent Patterns in Parallel Episodes with a Graded Notion of Synchrony and Selective Participation

Rossum, G. V. (1993). Python for unix/c programmers

the NLUUG najaarsconferentie. Dutch UNIX users

group.

Torre, E., Picado-Muino, D., Denker, M., Borgelt, C., and

un, S. (2013). Statistical evaluation of synchronous

spike patterns extracted by frequent item set mining.

Frontiers in Computational Neuroscience, 7.

Tsourakakis, C., Bonchi, F., Gionis, A., Gullo, F., and

Tsiarli, M. (2013). Denser than the densest subgraph:

Extracting optimal quasi-cliques with quality guar-

antees. In Proc. 19th ACM SIGMOD Int. Conf. on

Knowledge Discovery and Data Mining (KDD 2013,

Chicago, IL), pages 104–112, New York, NY, USA.

ACM Press.

Zaki, M. J., Parthasarathy, S., Ogihara, M., and Li., W.

(1997). New algorithms for fast discovery of associa-

tion rules. In Proc. 3rd Int. Conf. on Knowledge Dis-

covery and Data Mining (KDD 1997, Newport Beach,

CA), pages 283–296, Menlo Park, CA, USA. AAAI

Press.

NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications