Towards Ontology Exploration based on Path Structure Richness

Ond

rej Zamazal

University of Economics Prague, W. Churchill Sq. 4, 13067, Prague, Czech Republic

Keywords:

Path Diversity, Path Richness, Shortest Path, Ontology Richness, Ontology Exploration, OWL, Semantic Web.

Abstract:

This paper presents an approach of path structure richness based ontology exploration. We focus on global

richness as a way of characterizing ontology path richness in addition to using local richness to locate typical

rich path structures for a given ontology. Ontology exploration is performed by extracting the shortest paths

as a simpliﬁed ontology excerpt or summary. Proposed path structure richness metrics are based on shortest

paths, their relationship diversity and their occurrences. We describe our general motivation, basic concepts,

preliminary experimentation and future work for ontology exploration based on path structure richness.

1 INTRODUCTION

Discovering characteristics of an ontology is an im-

portant task in ontology engineering. Clearly char-

acterized ontologies enable ontology users to select

the proper ontology for use or reuse. While ontology

summarization techniques provide a compressed ver-

sion of a given ontology, providing important infor-

mation for the user (Li et al., 2010a), ontology eval-

uation measures the quality of an ontology by ana-

lyzing its diverse aspects, e.g. structure (Vrande

2009). Typically, the results from ontology evaluation

and ontology exploration are used by ontology sum-

marization algorithms. One example of this is the key

concept extraction method (Li et al., 2010b), which

generates ontology summaries in the KC-Viz tool.

In this paper we introduce path structure richness

based ontology exploration as a method of ontology

evaluation and characterization. We base our a graph-

based ontology exploration on the extraction of short-

est paths between ontology classes as a way of gener-

ating simpliﬁed ontology excerpts or summaries. By

generalizing shortest paths into path structures with

placeholders, we analyze occurrences of structures of

a certain type and, in particular, inspect the richness

of such path structures. By inspecting path structure

richness we locate typical paths for given ontology.

Locating typical paths is an important activity for bet-

ter understanding the design of an ontology. In addi-

tion, we measure ontology-wide path structure rich-

ness metrics to provide overall ontology characteris-

tics. Such ontology characterization can help users

to quickly recognize ontologies that have rich paths,

which can be useful for testing ontology visualization

techniques, for example.

The paper is structured as follows. Section 2 in-

troduces basic concepts. Section 3 describes local and

global path structure based richness metrics. Section

4 provides preliminary experimentation with richness

metrics applied on ﬁve selected ontologies and on on-

tologies from the Linked Open Vocabularies (LOV)

portal.

Section 5 presents a brief overview of related

work and Section 6 wraps up the paper.

2 PRELIMINARIES

The path structure richness deﬁned in this paper is

calculated by considering the graph representation of

an ontology. This graph is an edge-labeled directed

multigraph G = (V, E), where V is a ﬁnite set of ver-

tices representing the named entites and anonymous

classes deﬁned in the ontology. E ⊆ V ×

∑

×V is

a ternary relation whose elements (v

, l

, v

) are lan-

guage edges, where l ∈

∑

∪

∑

∪

∑

is the set of

all the language constructs in the ontology language

for deﬁning entities plus

∑

and

∑

, i.e.

∑

is equiva-

lent to the set of properties in the OWL vocabulary,

e.g. EquivalentTo.

∑

is the set of inverse vari-

ants of the language constructs from

∑

(see Table 1)

and

∑

are relationships which depict components of

anonymous classes (e.g. andComponent from Object-

http://lov.okfn.org/

We use the Manchester syntax for OWL constructs:

http://www.w3.org/TR/owl2-manchester-syntax/.

Zamazal, O..

Towards Ontology Exploration based on Path Structure Richness.

In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 2: KEOD, pages 245-250

ISBN: 978-989-758-158-8

245

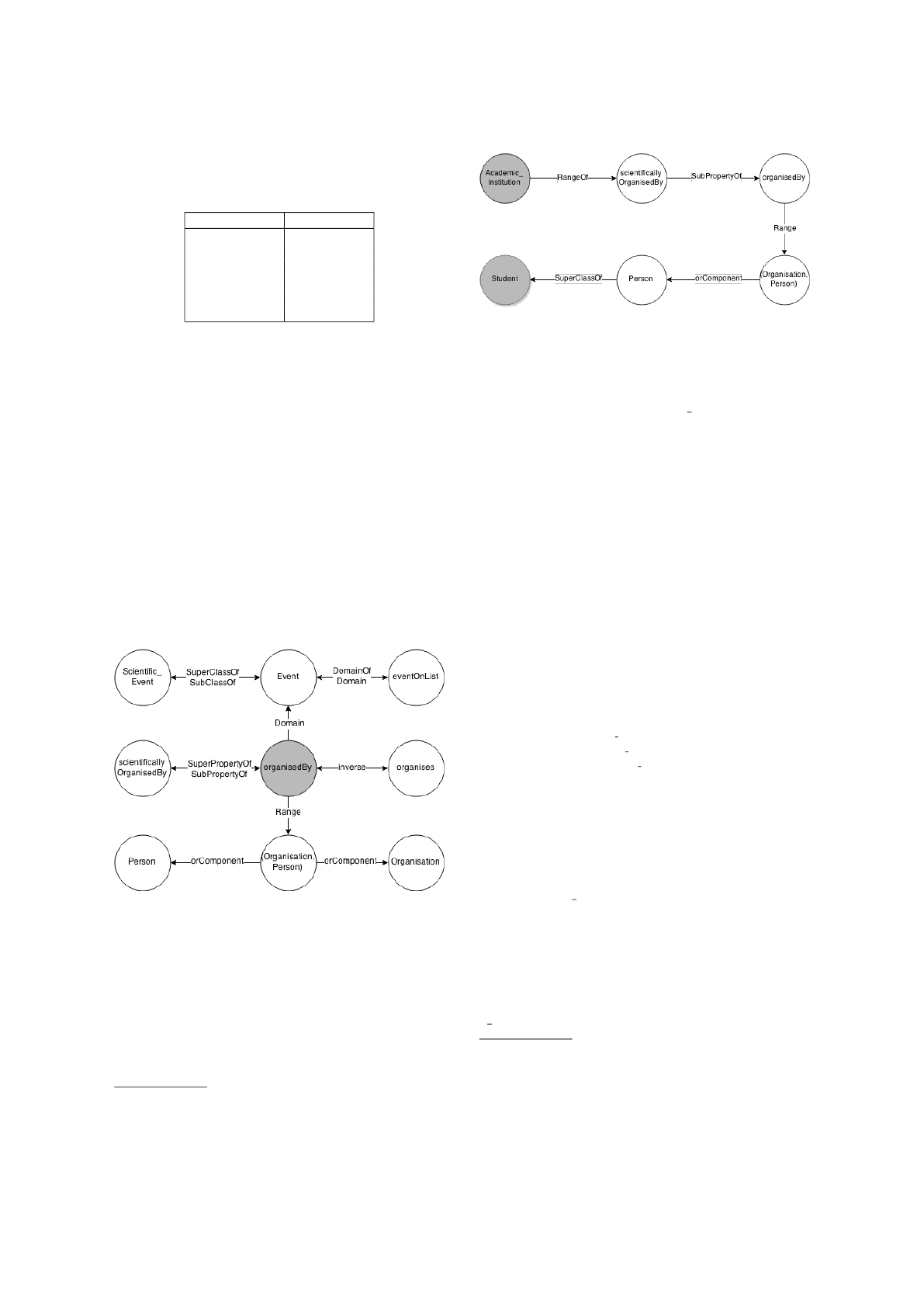
Table 1: The inverse edges for the OWL language con-

structs employed in our graph-based representation. There

is a character representing each edge in the parentheses.

Language Construct Inverse Edge

SubClassOf (C) SuperClassOf (B)

Domain (E) DomainOf (e)

Range (G) RangeOf (g)

Types (s) HasInstance (S)

EquivalentTo (D) EquivalentTo (D)

inverse (F) inverse (F)

IntersectionOf construct etc.). Labels to edges are as-

signed by function label(l) : L →

∑

∪

∑

∪

∑

. We

extended graph representation of an ontology used

in (Doran et al., 2008) with considering anonymous

classes as nodes and with

∑

and

∑

relationships.

According to the deﬁnition of our graph represen-

tation, an anonymous class can be a vertex of a graph.

Edges can connect anonymous classes to their com-

ponents. This enables us to capture the larger con-

nected path structure, which ideally still deals with a

similar topic. On the other hand, components consti-

tuting an anonymous class are not directly mutually

connected in our graph representation. Figure 1 de-

picts a snippet of the conference organization ekaw

ontology centered around the organisedBy property,

which illustrates the orientation of edges in our graph

representation.

Figure 1: A snippet of the ekaw ontology.

We restrict ourselves to paths in our graph-based

ontology representation for exploring ontology struc-

tures. An ontology typically contains many differ-

ent paths between entities. In order to reduce the

large space of paths to be explored we only explore

the shortest paths between classes. Shortest path is

a path with a minimum number of edges between

given named classes. We believe that the shortest

http://oaei.ontologymatching.org/2014/conference/

data/ekaw.owl

Figure 2: Concrete path example.

paths (from now on simply paths) provide, to some

extent, meaningful structures characterizing a given

ontology. For example, Figure 2 visualizes the path

between named classes Academic Institution and Stu-

dent also going through anonymous class represented

by a disjunction in the ekaw ontology. To increase

the semantic compactness of shortest paths, we ignore

paths with the most general class owl:Thing being in-

cluded as a vertex, since relations going through the

owl:Thing concept can literally connect anything. For

similar reasons, we ignore paths containing a Disjoin-

tWith edge that connects semantically rather different

named classes, e.g. Event and Person.

For discovering shortest paths we use our Path-

Searcher tool (Zamazal, 2015).

In our automatic ex-

ploration we do not analyze concrete paths but we

consider path structures as paths with placeholders

instead of concrete named or anonymous classes.

Placeholders to vertices are assigned by function

placeholder(v):

placeholder(v) :V →











?class (1) if v is a named class,

?object

property (2) if v is a object property,

?datatype property (3) if v is a datatype property,

?anonymous class (4) if v is an anonymous class,

?individual (5) if v is an individual.

(1)

In our representation, each vertex is represented

by a number in parentheses, as shown in Equation 1,

and each edge is represented by a character, as exem-

pliﬁed in Table 1.

Function c paths(G) returns all concrete paths

from G between named classes, and paths(G) returns

all path structures from G between named classes.

Path length, length(p), is the number of edges in path

p. Since we want to treat path structures of a certain

length separately, we deﬁne path structure stratum as

the path structures of a certain length where function

c paths

l=n

(G) returns all concrete paths of length n

http://owl.vse.cz:8080/PathSearcher/

From now on, we will use term path if it does not mat-

ter whether it is concrete path or path structure, otherwise

we will use concrete path or path structure notions to dis-

tinguish between them.

KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development

246

from ontology graph G. For example, the concrete

path (and its corresponding path structure) between

named classes Academic Institution and Student from

the ekaw ontology depicted in Figure 2 has a length

of 5.

3 PATH STRUCTURE BASED

RICHNESS METRICS

3.1 Local Path Structure Metrics

A path can contain different types of edges. Although

a path can have consist entirely of one type of edge,

every edge of a path could also be of a different type.

In order to capture the degree of edge-type diversity

within a path we deﬁne path diversity as follows:

diversity(p) =

|edge types(p)|

length(p)

| diversity(p) ∈ (0, 1].

(2)

where function edge types(p) returns a set of unique

edge types involved in the path p. Mutually inverse

edges are counted just once (e.g. SuperClassOf and

SubClassOf). For example, the path depicted in Fig-

ure 2 has its diversity equal to 0.8.

Comparing paths based on their diversity is dis-

torted by unequal path lengths. Thus, we add a rel-

ative length component. Further, path structures are

instantiated by a different number of concrete paths

within one ontology, f req(p). Regarding the impor-

tance of path structure, we assume that the more in-

stances of a path structure, the more important this

path structure is for the given ontology. This can be

captured by the relative frequency component. Hence,

we deﬁne path structure richness, psr, of path struc-

ture p within given ontology as follows:

psr(p, maxLength) =

f req(p)

|c paths(G)|

length(p)

maxLength(G)

×diversity(p).

(3)

where maxLength is the maximum length of path

structures to be considered. psr reﬂects the relative

richness of path structure. Generally, psr is higher

than zero and lower than 1. It is equal to 1 if there

is only one path structure of diversity 1. This equa-

tion favors longer path structures, which corresponds

to the intuition that the longer (to a certain extent)

the path structure is, the higher the probability that

it includes a typical structure for the given ontology.

Moreover, larger path structures are composed from

shorter path structures. Thus, inspecting reasonably

large path structures naturally involves the analysis

of its shorter components and lowers the chance of

overlooking potentially interesting typical structures

for the given ontology. Based on our experimenta-

tion, a reasonable size for path structures is a length

of 5. Although, psr equation could be simpliﬁed by

breaking down its diversity(p) component and elimi-

nating its length(p) part, we keep it in this form since

we want to emphasize the origin of each component.

For the path structure in Figure 2 psr is 0.0029 since

|c paths(G)| = 1345, f req(p) = 5, length(p) = 5,

diversity(p) = 0.8 and maxLength was set to 5.

3.2 Ontology-wide Path Structure

Metrics

Besides measuring local richness of path structures,

we measure ontology path structure richness by de-

veloping a metric based on a rationale similar to the

one we used to develop the local path structure rich-

ness metrics.

In order to provide a more detailed means for

path structure richness based ontology exploration,

we ﬁrst consider path structure richness for each

path structure stratum separately within an ontology,

psr

ont

(G, n):

psr

ont

(G, n) =

∑

p∈paths(G)|length(p)=n

f req(p) × diversity(p)

|c paths

l=n

(G)|

(4)

Global ontology path structure richness,

global

psr ont

(G, maxLength), is deﬁned as an

average of psr

ont

(G, n) across all path structure strata

up to path structure stratum with a maximum length,

maxLength:

global

psr ont

(G, maxLength) =

maxLength

∑

n=1

psr

ont

(G, n)

maxLength

(5)

Both these ontology metrics can be generally

higher than zero and lower or equal to 1.

4 PRELIMINARY EXPERIMENTS

We performed two experiments on ﬁve selected on-

tologies and one experiment on LOV ontologies.

First, we analyzed the behaviour of local path struc-

ture metrics by inspecting path structures within the

ontologies in Section 4.1 and second, a behaviour of

ontology-wide path structure metrics on the ontolo-

gies in Section 4.2.

Towards Ontology Exploration based on Path Structure Richness

247

Table 2: The top three path structures for the wine,

ekaw, gr and pwo ontologies according to psr values.

B=SuperClassOf, C=SubClassOf, D=EquivalentTo,

E=Domain, e=DomainOf, G=Range, g=RangeOf,

t=andComponent and l=orComponent.

Str. path (wine) freq dist. diver. psr

1B1B1G2t4D1 220 5 0.8 .0531

1B1G2t4D1 170 4 1 .0411

1B1t4D1 111 3 1 .0201

Str. path (ekaw) freq dist. diver. psr

1B1G2e1C1C1 53 5 0.6 .0236

1B1l4G2e1C1 35 5 0.8 .0208

1B1C1 134 2 0.5 .0199

Str. path (gr) freq dist. diver. psr

1g2E4l1 46 3 1 .1215

1C1g2E4l1 26 4 1 .0916

1g2E4l1B1 23 4 1 .0810

Str. path (pwo) freq dist. diver. psr

1E2g1C1 14 3 1 .0112

1G2e1C1 11 3 1 .0088

1E2g1C1C1 10 4 0.75 0.0080

For our experimentation we selected 5 ontologies,

which had been previously manually inspected.

ﬁrst selected one very rich ontology wine and one less

rich ontology ekaw. Then we added two relatively

rich ontologies (gr and pwo) and one simple ontology,

taxon, from the Linked Open Vocabularies repository.

We set the parameter maxLength to ﬁve for three

reasons based on our experimentations: it turns out

that (1) longer path structures rarely disclose inter-

esting rich path structures, (2) longer path structures

already include shorter path structures and (3) for

longer ontology path structures, richness usually be-

gins to decrease.

4.1 Experiments with Local Path

Structure Metrics

For each of ﬁve selected ontologies we consider the

three top path structures (and their corresponding con-

crete paths) with regard to their path structure richness

(psr) values.

The Wine Ontology: deals with the wine domain,

i.e. it speciﬁes categories of wine and relates them to

suitable meal courses. This ontology imports the food

ontology,

which our ontology representation also

Ontologies and further material from our experiments,

are available at: http://owl.vse.cz:8080/KEOD-2015/

http://www.w3.org/TR/2003/PR-owl-guide-20031209/

food

considers. The main purpose of the ontology is ed-

ucational. Three path structures (see Table 2) having

the highest psr values are very similar to each other.

The path structure, 1B1G2t4D1, is included in the ﬁrst

one, 1B1B1G2t4D1. These two path structures deal

with complete deﬁnition of different courses using in-

tersection of named class and anonymous class with

universal restriction. This path structure is typically

terminated with food, e.g. NonRedMeatCourse and

PastaWithWhiteSauce. While those two path struc-

tures connect any type of food, its shorter variant,

1B1t4D1, already connects course to its related food,

e.g. ShellﬁshCourse and NonOysterShellﬁsh.

The ekaw Ontology: is a relatively rich confer-

ence organization ontology from Ontology Alignment

Evaluation Initiative, the conference track. It concep-

tualizes people and workﬂows dealing with organiz-

ing Ekaw conference, e.g. chairs, articles, reviewing

processes, etc. The path structure with highest value

of psr, 1B1G2e1C1C1, captures the relationship be-

tween a speciﬁc document and speciﬁc type of per-

son, for example, Flyer and Presenter. Next, the path

structure, 1B1l4G2e1C1, relates an event concept to

a speciﬁc person organising the event, e.g. Scien-

tiﬁc Event and Agency Staff Member. It also relates a

speciﬁc paper type to its possible presentation mode,

e.g. Poster Paper and Invited Talk. Path structure

1B1C1 is typical taxonomy path capturing siblings,

e.g. Conference Session and Workshop Session.

The gr Ontology: is the GoodRelations ontology

which is a relatively rich, widely applied vocabulary

for describing goods. In this case, all three path struc-

tures having highest psr values share shorter path

structure, 1g2E4l1, where a particular class is in the

range of some property having a domain speciﬁed by

an union of several concepts. For example, this en-

ables representing a reiﬁed relationship, e.g. Offer

is related to QuantitativeValueInteger, PriceSpeciﬁ-

cation or Licence via different object properties, e.g.

hasPriceSpeciﬁcation. Longer paths from Table 4 add

specialization or generalization to concepts on each

side of the path structure 1g2E4l1.

The pwo Ontology: is the Publishing Workﬂow

Ontology for describing the workﬂow associated with

the publication of a document. Its design is based

on many ontology design patterns. Hence, ontology

imports play a crucial role. Shorter structure path,

1E2g1C1 (or 1G2e1C1), reﬂects a situation where

property deﬁnition includes more general class on the

one side of the structure, e.g. between a TimeIn-

dexedSituation and an Agent. This is part of the time-

KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development

248

indexed situation pattern.

Finally, the path structure

1E2g1C1C1 extends the path structure 1E2g1C1 with

one layer of generalization for a range of a certain

property, e.g. between WorkﬂowExecution and De-

scription via property isSatisﬁedBy.

The Taxon Ontology: is a simple ontology contain-

ing the biomedical classiﬁcation of organisms. This is

reﬂected by the discovered path structures, since there

are only path structures containing SuperClassOf and

SubClassOf relations, e.g. the highest psr value,

0.0274, has the path structure 1B1C1 of freq=91.

4.2 Experiments with Ontology-wide

Path Structure Metrics

Table 3 summarizes the basic ontology characteris-

tics (nr. of entities, ontology complexity, nr. of

concrete paths and nr. of path structures) and pro-

vides the ontology richness metrics psr

ont

(G, n) for

different path structure strata

and overall richness

global

psr ont

(G, 5). Inspecting the results of global

ontology path structure richness, global

psr ont

, we can

see that wine and gr have the highest values, while

taxon has the lowest one. Further, psr

ont

(G, n) can be

used for comparisons among all ontologies regarding

a certain path structure stratum. We can see that gr

ontology dominates for all path structure strata ex-

cept distance of two, where the wine ontology has

a higher richness value. Next, comparing ontologies

according to their relative path structure occurrences

(

|paths(G)|

|c paths(G)|

) we can see that pwo has a relatively high

number of the different path structures and taxon has

relatively few paths of the different structure. This

can be explained by the fact that taxon only contains

subsumptions, while pwo contains many diverse but

infrequent paths. All these results are promising since

they more-or-less correspond to ontology richness na-

ture of explored ontologies.

Finally, we applied computation of global ontol-

ogy path structure richness, global

psr ont

, on all on-

tologies from the LOV portal available via the “On-

line Ontology Set Picker” (OOSP) tool.

Table 4

provides cumulative numbers for ontologies having

less than a certain value of global

psr ont

corresponding

to values computed on the ﬁve explored ontologies.

http://www.ontologydesignpatterns.org/cp/owl/

timeindexedsituation.owl

Due to the uniformity of path structures we do not pro-

vide table with other path structures and values.

We omitted psr

ont

(G, 1) which is always 1.

The OOSP provides an easy access to 97% of all LOV

ontologies from http://owl.vse.cz:8080/OOSP/

Table 3: Path structure richness metrics for ﬁve ontologies.

The highest values per metrics are in bold.

Metrics gr wine pwo taxon ekaw

nr. of entities 186 361 183 97 107

complexity SHI(D) SHOIN(D) SHIQ(D) ALHI(D) SHIN

|c paths(G)| 227 3309 745 662 1345

|paths(G)| 40 250 256 19 133

|paths(G)|

|c paths(G)|

17% 7% 34% 3% 10%

psr

ont

(G, 2) .675 .786 .777 .500 .532

psr

ont

(G, 3) 1.000 .834 .709 .333 .464

psr

ont

(G, 4) .966 .757 .644 .250 .563

psr

ont

(G, 5) .728 .672 .607 .200 .601

global

psr ont

.873 .810 .747 .456 .632

avg(psr) .0153 .0023 .0018 .0105 .0030

Table 4: Cumulative numbers of ontologies from the LOV

portal having less than a certain value of global

psr ont

global

psr ont

.456 .632 .747 .810 .873 1.0

# ontologies 141 238 332 388 439 451

Out of 461 ontologies available via OOSP, we

could process 451 ontologies which makes our exper-

iment signiﬁcant wrt. LOV ontologies. In 57 cases,

the resultant global ontology path structure richness

was zero since there were no paths within the ontolo-

gies, e.g. ontologies only with annotation properties.

If we consider the results of our exploration of ﬁve

manually inspected ontologies we can interpret Ta-

ble 4 as it follows:

• Almost one third of all ontologies have lower

global richness than the taxon ontology.

• More than half of all ontologies have lower global

richness than the ekaw ontology.

• Slightly more than two third of all ontologies have

a global richness lower than the pwo ontology.

• 86% of all ontologies have a global richness lower

than the wine ontology.

• Finally, almost all ontologies have a global rich-

ness lower than the gr ontology.

5 RELATED WORK

Regarding richness metrics, the most relevant work is

by Tartir et al. (Tartir et al., 2005), where a schema

and its population metrics are used to characterize an

ontology. They use relationship richness, deﬁned as a

ratio of the number of relationships in the schema to

the number of all subclasses, and the number of rela-

tionships. In our work we focus not only on the global

richness characteristics, but we also aim at the local

Towards Ontology Exploration based on Path Structure Richness

249

richness of structures. Moreover, authors in (Tartir

et al., 2005) only consider subsumption relations and

non-subsumption ones as only two kinds of relation-

ships, but we distinguish all the OWL language prop-

erties employed in the ontology.

An occurrence analysis of particular structures

(list, tree, multitree and diamond) was done on a large

number of ontologies by Wang et al. in (Wang et al.,

2006). They consider more complex structures, but

they only consider subsumption as a possible edge

and they do not measure richness.

Regarding discovery of frequent structures, the

most relevant is work by Mikroyannidi et al. (Mikroy-

annidi et al., 2011). They introduce an approach for

detecting syntactic regularities applying generalisa-

tion with placeholders on axioms, lexical patterns and

clustering. Later, they extended it with semantic regu-

larities by including entailments. While our approach

also considers placeholders, we do not consider se-

mantic regularities, and we focus on the richness as-

pect of structure.

Regarding ontology and dataset summaries, our

shortest paths based approach is related to (Heim

et al., 2009). They extract a graph covering rela-

tionships between two entities from large knowledge

bases. However, while they focus on relationships

within RDF knowledge bases, we merely concentrate

on exploration of an ontology TBox.

6 CONCLUSIONS AND FUTURE

WORK

This paper presents an approach of path structure

richness based ontology exploration. Our exploration

approach contributes to the understanding of an ontol-

ogy by identifying its typical paths. Our preliminary

experimentation shows promising results in terms of

locating typical rich path structures and comparing

global path structure richness among ontologies.

In order to support the whole exploration ap-

proach, we plan to provide an interactive path struc-

ture explorer where recurrent rich path structures

would be considered not only within one ontology but

also across ontologies. Considering rich path struc-

tures across many ontologies could eventually point

out broadly present typical path structures and, thus,

perhaps broadly accepted ontology design patterns.

We plan to further experiment with a different set-

ting of shortest path search, e.g. various forbidden

edges and consideration of inferred axioms. We also

plan to employ data mining techniques for analyz-

ing relation between values of our ontology richness

metrics and other ontology metrics (e.g. from (Tar-

tir et al., 2005)). Currently, we restrict ourselves to a

rather linear structure, but will consider more com-

plex structures (e.g. diamond shape (Wang et al.,

2006)). Similarly to measuring centrality in KC-Viz

summarization (Li et al., 2010b), we plan to extend

our work with assessing the importance of entities ac-

cording to the structure paths in which they are in-

volved. Finally, we envision employing these metrics

into our OOSP tool to support ontology developers

and researchers in their experimental work.

ACKNOWLEDGEMENTS

This work has been supported by the CSF grant

no. 14-14076P, “COSOL – Categorization of Ontolo-

gies in Support of Ontology Life Cycle” and by long

term institutional support of research activities by

Faculty of Informatics and Statistics, University of

Economics, Prague.

REFERENCES

Doran, P., Tamma, V., Palmisano, I., Payne, T. R., and Ian-

none, L. (2008). Evaluating ontology modules using

an entropy inspired metric. In Web Intelligence and

Intelligent Agent Technology, pages 918–922. IEEE.

Heim, P., Hellmann, S., Lehmann, J., Lohmann, S., and

Stegemann, T. (2009). Relﬁnder: Revealing relation-

ships in rdf knowledge bases. In Semantic Multime-

dia, pages 182–187. Springer.

Li, N., Motta, E., and d’Aquin, M. (2010a). Ontology sum-

marization: an analysis and an evaluation. In Intern.

Work. on Evaluation of Sem. Technologies. CEUR.

Li, N., Motta, E., and Zdrahal, Z. (2010b). Evaluation of

an ontology summarization approach. In EKAW 2010

(posters and demos). CEUR.

Mikroyannidi, E., Iannone, L., Stevens, R., and Rector, A.

(2011). Inspecting regularities in ontology design us-

ing clustering. In 10th International Semantic Web

Conference, pages 438–453. Springer.

Tartir, S., Arpinar, I. B., Moore, M., Sheth, A. P., and

Aleman-Meza, B. (2005). Ontoqa: Metric-based on-

tology quality analysis. In Worksh. on Knowl. Acqui-

sition from Distributed, Autonomous, Semantic. Het-

erogeneous Data and Knowl. Source.

Vrande

c, D. (2009). Ontology evaluation. In: Handbook

on Ontologies. Springer, 2nd edition.

Wang, T. D., Parsia, B., and Hendler, J. (2006). A survey

of the web ontology landscape. In 5th International

Semantic Web Conference, pages 682–694. Springer.

Zamazal, O. (2015). Online ontology shortest paths

searcher. In Proceedings of the 11th International

Conference on Semantic Systems, SEMANTICS ’15,

pages 204–206, New York, NY, USA. ACM.

KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development

250