A New Approach to Aggregation of Inconsistent Expert Opinions
Andrzej Piegat and Karina Tomaszewska
Faculty of Computer Science and Information Technology
West Pomeranian University of Technology, Szczecin, Poland
Keywords: Horizontal Membership Function, RDM-method, Fuzzy Sets, Expert Opinions.
Abstract: The aim of this paper is to present a new way of aggregation two expert opinions. These opinions are
disjoint and inconsistent, thus it is difficult to find a common solution using currently known methods. The
authors suggest using horizontal membership function and RDM (Relative Distance Measure) method to get
complete and unambiguous result. A general outline of this approach is presented and its equations are
shown. The numerical example is given to illustrate the efficiency of the proposed method to practical
issues in decision-making problems.
1 INTRODUCTION
Aggregation of data items delivered by various
sources, of expert opinions, of measurements from
various sensors and measuring instruments is at
present intensively investigated because of the
tendency to automate decision-making. However,
this task is very difficult because aggregated data
items usually are uncertain (expressed as
distributions of possibility or probability density)
and they are more or less inconsistent. Aggregation
of e.g. few expert opinions expressed in forms of
distributions consists on determining of one
distribution which in the best way represents the
experts’ opinions. If the distributions are at least
partly consistent (their supports have common part
but models are not identical) then some methods in
the subject literature can be found, which allow for
aggregation (Dubois, 2004). If the opinions are
considerably inconsistent and have no common
range then the standard aggregation methods are e.g.
AND, OR-operations, linear opinion pooling
(O’Hagan, 2006). Unfortunately they give strongly
disputable results, which rather cannot be applied in
practice.
Aggregation of inconsistent expert
opinions, when the quality of the experts is
unknown, can be understood as: a) a possibility
distribution derived from experts distributions with
certain required conditions imposed by an expert; b)
a possibility distribution derived from experts
distributions representing their opinions according to
the accepted criterion of optimality (sum of absolute
errors, sum of squared errors, etc).
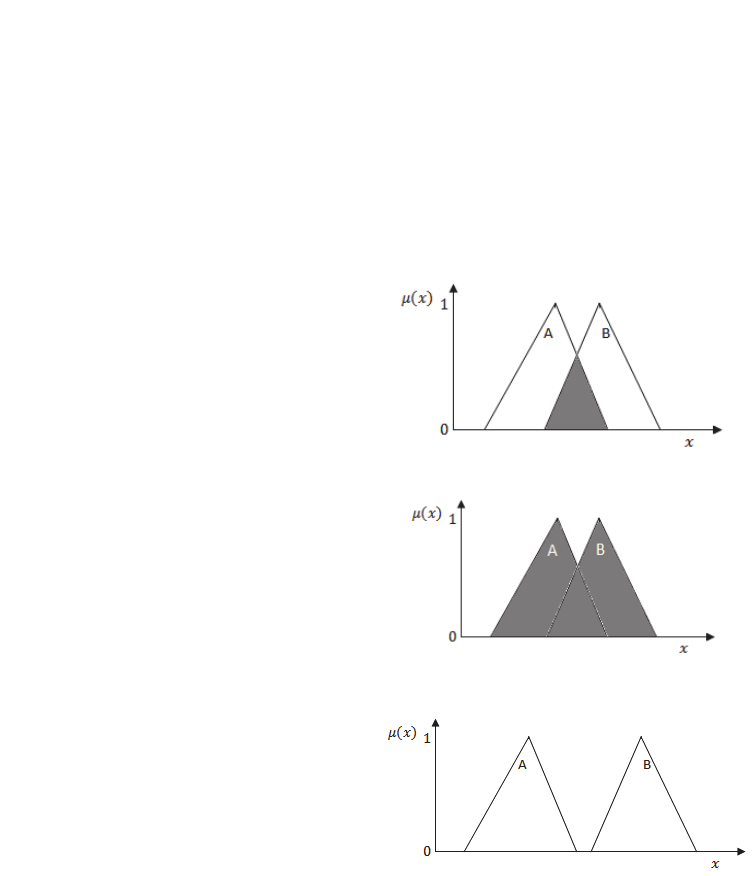
Figure 1a: AND (MIN) operation for joint opinions.
Figure 1b: OR (MAX) operation for joint opinions.
Figure 1c: Disjoint opinions.
176
Piegat, A. and Tomaszewska, K..
A New Approach to Aggregation of Inconsistent Expert Opinions.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 2: FCTA, pages 176-179
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

However, inconsistency of expert opinions
occurs frequently (Beg, 2013; Herrera-Viedma,
2004; Son, 2014) and has to be solved because it
concerns not only decision-making by people but
also by technical devices as automatic alarms,
automatic airplane defence devices, controllers
(Gegov, 2015). There are several aggregation
strategies for combining different estimates,
including: null aggregation, intersection, envelope,
Dempster’s rule and its modifications, Bayes’ rule
and logarithmic pool but they are Type-1 methods
and used only when the borders of fuzzy
numbers/intervals are certain (Ferson, 2003). A new
and interesting possibility of inconsistent opinions
aggregation opens combination of fuzzy sets Type-2
theory (FST2) developed mainly by J. Mendel and
co-workers (Mendel, 2002), and the concept of
horizontal membership functions (Piegat, 2015;
Tomaszewska, 2015). In this paper an aggregation
method of two inconsistent expert opinions will be
shown. Aggregation of three or more opinions and
mathematical properties of this operation will be
presented in next papers of authors.
2 METHODOLOGY
In this paper a horizontal membership model will be
used (Piegat, 2015). Constructing horizontal MFs
requires using multidimensional RDM interval-
arithmetic based on relative-distance-measure
variables. This method is a new approach to interval
arithmetic. In this method an information granule is
given as a variable, which has a value contained in
interval
,̅, where is the lower limit and ̅ is
the upper limit of the interval. Thus variable can
be described with formula (Tomaszewska, 2015):
,̅:
̅ ,
0,1
These distributions can have a great meaning in the
case of complex mathematical formulas or schemes.
RDM-variable is used in horizontal MFs in the way
that the function of fuzzy number assigns two values
of :
and
for one value of and the
relative distance between these two values of is
. On the left border
0 and on the right
border
1. The transitional segment
can be
defined by function (Piegat, 2015):
,
∈ 0; 1
Inconsistent opinions can be interpreted as follows:
the experts in different way evaluate position of the
minimal (left)
and of maximal (right) border
of their evaluations. Thus, the left border
and the
right border
of the aggregated evaluation is
uncertain (g means operation of aggregation). A
possible left border
of aggregated MF
in terms of interval FSs Type-2 is called left
embedded border and a possible right border
is
called right embedded border. Fig.2. shows
denotations used in further formula derivations.
Figure 2: Membership functions
,
and one
possible aggregated function
of Type-1.
In Fig.2.
and
variables are left/right border
transformation and
is inner RDM variable of
embedded MF Type-1. Formulas (1)-(4) give values
for points
,
,
,
which characterize
embedded MFs- Type-1:
where
0,1
and
(1)
(2)
where
0,1
and
(3)
(4)
On the basis of formulas (1)-(4) a horizontal model
of the left uncertain border of the embedded
aggregated MF is achieved.
where
0,1
and
0,1
(5)
And the right uncertain border of the aggregated MF
is analogously determined:
(6)
where
0,1
and
0,1
The full horizontal model of the aggregated MFs
takes the following form:
where
0,1
and
0,1
(7)
The numerical example described in next section
A New Approach to Aggregation of Inconsistent Expert Opinions
177
shows how to use in practice above equations to
aggregate two inconsistent expert opinions.
3 NUMERICAL EXAMPLE
Two experts made assessments, but their opinions in
form of two triangular membership functions are
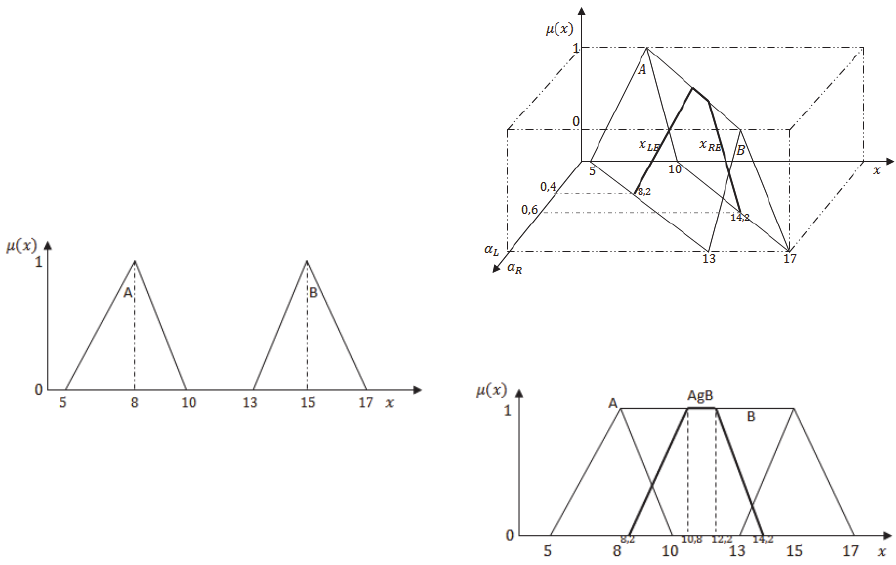
disjoint. Fig.3. presents these opinions.
Figure 3: Two inconsistent expert opinions.
The first step to get the full horizontal model of the
aggregated MFs is to determine the possible tops of
aggregated membership function using equations
(1)-(4):
58
,
87
,
87
,
107
, where
.
Hence, the left and right embedded borders are
achieved:
58
3
107
2
where
and
,
0,1
and
0,1
The full horizontal model of these two
inconsistent opinions takes form:
58
3
5 7
8
5
The formula
is multidimensional function
and it depends on four parameters
,
,
,
. In addition, if the values of
variables
and
are the same the result
is
triangular membership functions, if they are
different then it takes trapezoidal MF. E.g. if
0
and
0 then
53
5 5 and if
1 and
1 then
132
4
4. The result for different values of
and
is
presented in Fig.4.
The exact result of aggregation of two
inconsistent expert opinions is a multidimensional
granule as presented in Fig. 4. For practical use we
can seek for low-dimensional representation in the
form of optimal distributions representing full
multidimensional solution (as shown in Fig. 5.).
Figure 4: Visualization of 4D horizontal membership
function
,
,
Type-2 and one of embedded
MF for
0,4and
0,6.
Figure 5: Visualization of 4D horizontal MF
,
,
Type-2 and one embedded MFT1 for
0,4and
0,6in 2D-space.
It can be assumed that in some problems the
parameters
and
can mean the credibility of
expert opinions and setting the appropriate values of
them makes
function only 2-dimensional.
4 CONCLUSIONS
Inconsistent FSs A and B generate one fuzzy set
Type-2 which is a family of embedded fuzzy sets
Type-1. It means that the true but precisely unknown
x-value that was evaluated by the experts A and B
can be contained in one of FSsT-1 imbedded in the
achieved FST-2, which membership function is
visualized in Fig.4. Each possible embedded MFT1
can be achieved by choice of values of RDM
variables. Interval-valued fuzzy sets theory and
horizontal RDM membership functions allow to
aggregate uncertain fuzzy sets which express
inconsistent expert opinions. Each opinion delivers
right and left border of fuzzy set. Two opinions
deliver two right and two left borders. It means that
the aggregated borders are uncertain and they
generate fuzzy set with uncertain borders. Hence the
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
178

aggregated MF has uncertainty of higher order than
each of the single component opinions.
REFERENCES
Beg, I., Rashid, T., 2013. A democratic preference
aggregation model, Journal of Uncertainty Analysis
and Applications, A Springer Open Journal.
Dubois, D., Prade, H., 2004. On the use of aggregation
operations in information fusion processes, Fuzzy Sets
and Systems. No 142.
Ferson, S., Kreinovich, V., Ginzburg, L., Myers, D.S.,
Sentz, K., 2003. Constructing Probability Boxes and
Dempster-Shafer Structures, Sandia National
Laboratories, Report SAND2002-4015.
Gegov, A. et all., 2015. Rule base simplification in fuzzy
systems by aggregation of inconsistent rules, Journal
of Intelligent&Fuzzy Systems. No 28 (3).
Herrera-Viedma, E., et all, 2004. Some issues on
consistency of fuzzy preference relation, European
Journal of Operational Reserch. No 154.
O’Hagan, A., et all., 2006. Uncertain judgments. Eliciting
experts’ probabilities,Wiley, Chichester.
Mendel, J., John, R., 2002. Type-2 fuzzy sets made simple,
IEEE Transactions on Fuzzy Systems. Vol.10, No.2.
Piegat, A., Landowski, M., 2015. Horizontal membership
function and examples of its applications, Online
journal: International Journal of Fuzzy Systems.
Son, L.N., 2014. Consistency test in ANP method with
group judgment under intuitionistic fuzzy environment,
International Journal of Soft Computing and
Engineering. Vol.-4, Issue 3.
Tomaszewska, K., Piegat, A., 2015. Application of the
horizontal membership function to the uncertain
displacement calculation of a composite massless rod
under a tensile load, In A. Wilinski et all. (Eds) Soft
Computing in Computer and Information Science.
A New Approach to Aggregation of Inconsistent Expert Opinions
179
