A Heteroassociative Learning Model Robust to Interference
Randa Kassab and Fr
´
ed
´
eric Alexandre
Inria Bordeaux Sud-Ouest, 200 Avenue de la Vieille Tour, 33405, Talence, France
LaBRI, Universit
´
e de Bordeaux, Bordeaux INP, CNRS, UMR 5800, Talence, France
Institut des Maladies Neurod
´
eg
´
en
´
eratives, Universit
´
e de Bordeaux, CNRS, UMR 5293, Bordeaux, France
Keywords:
Associative Memory, Interference, Hippocampus.
Abstract:
Neuronal models of associative memories are recurrent networks able to learn quickly patterns as stable states
of the network. Their main acknowledged weakness is related to catastrophic interference when too many or
too close examples are stored. Based on biological data we have recently proposed a model resistant to some
kinds of interferences related to heteroassociative learning. In this paper we report numerical experiments
that highlight this robustness and demonstrate very good performances of memorization. We also discuss
convergence of interests for such an adaptive mechanism for biological modeling and information processing
in the domain of machine learning.
1 INTRODUCTION
Generalization is often reported as a desirable prop-
erty of artificial neural networks. This phenomenon
occurs if, when a network is presented with an ex-
ample it has never seen before, it is able to interpo-
late a satisfactory response from the combination of
close previously learned examples. Such a response
can be judged satisfactory not only because from a
limited learning phase the network behaves well in
a wider domain but also because in some sense learn-
ing went beyond specific cases and was able to extract
some general structures or regularities in the example
space. In some cases, however, this property might be
considered a flaw. This is the case for example when
there is no useful topography in the example space or
when the goal is to learn some arbitrary association.
Consider for example learning to associate a phone
number with a name: there is nothing to learn from
the euclidean distance between two such numbers and
you can in no way discover an association if it was not
instructed to you before. This contrasts the cases of
learning a general rule from a set of examples, as it is
for example studied with layered architectures like the
multilayer perceptron, versus learning by heart spe-
cific cases like in associative memories.
Neural models of associative memories have been
proposed with recurrent networks like the Hopfield
model (Hopfield, 1982) and the Willshaw model
(Willshaw et al., 1969). Based on classical connec-
tionist characteristics (like units with non linear acti-
vation functions and hebbian learning), the recurrent
architecture of these networks indicates that learning
is mainly focused on the inner characteristics of an ex-
ample to be memorized and not on the elaboration of
abstract representations in intermediate layers. Nev-
ertheless, some problems can appear if too close ex-
amples are learned. In such a case, the network might
elaborate an answer from the combination of several
learned examples; what would be called generaliza-
tion in other circumstances is called here interference.
As a consequence, models of associative memo-
ries are generally used as content addressable memo-
ries, where few prototypes are stored as stable states
of the network and noisy or incomplete patterns are
presented as inputs and reconstructed to the closest
stored example. Beyond this use as an autoassocia-
tive memory (where initial input and final result have
the same dimension), the adaptation to heteroassocia-
tive memory is straightforward: just virtually split the
recurrent network in two sets of neurons A and B. The
recurrent connectivity includes connections within A
and within B (seen as two autoassociative memories)
and between A and B (heteroassociative memory be-
tween the two sets of different dimension A and B).
As configurations of A+B are learned as prototypes,
proposing an incomplete pattern A (B neurons be-
ing set to 0) will result in the reconstruction of A+B,
yielding the answer B. The main acknowledged weak-
ness of these models is about their limited capacity of
Kassab, R. and Alexandre, F..
A Heteroassociative Learning Model Robust to Interference.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 3: NCTA, pages 49-57
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
49
storage and the associated risk of catastrophic inter-
ference when this capacity is exceeded or when too
close prototypes are stored (Graham and Willshaw,
1997; Knoblauch et al., 2010). The best solution to
this problem is to require a sparse coding, which in-
trinsically also limits the maximum number of stored
prototypes. An associated strategy is to orthogonal-
ize the inputs and project their encoding in higher di-
mensions, which results in larger weight matrices to
manipulate (McNaughton and Nadel, 1990).
Models of associative memory have also been
studied for their complementarity with classical neu-
ral models of pattern matching like the multilayer per-
ceptron and for the deep cognitive anchoring of this
complementarity. Indeed, it was proposed 20 years
ago (McClelland et al., 1995) that the brain exploits
complementary learning systems, with a slow and
procedural learning in the cortex, able to extract struc-
tures and regularities in the data and to generalize,
compared with a quick learning of novel information
in the hippocampus.
In a recent work, we have proposed a refinement
of hippocampal model (Kassab and Alexandre, 2015),
inspired from recent biological data (Samura et al.,
2008). These data report heterogeneities in the hip-
pocampal structure that might support the coexis-
tence of autoassociative and heteroassociative mem-
ories in this region. Specifically, the hippocam-
pus is a neuronal structure known to be involved in
episodic memory (Tulving, 1972), corresponding to
the storage of specific episodes including their con-
text and their emotional or motivational significance.
For example, the hippocampus in involved in contex-
tual learning of pavlovian conditioning (Carrere and
Alexandre, 2015), linking neutral stimuli and their
context to biologically significant events (reward and
punishment). Though primarily oriented toward bio-
logical modeling, we have also explained in (Kassab
and Alexandre, 2015) the interest of such a segre-
gation from an information processing point of view
(cf. the concluding section for a summary). In ad-
dition, we have also postulated an additional mecha-
nism for the association of autoassociative memories,
that might result in a more robust system, particularly
more resistant to interference. The goal of this paper
is to evaluate more precisely the performances of this
mechanism from an information processing point of
view.
In the next section, we will present this model
together with its formalism based on the associative
memory initially proposed by Willshaw (Willshaw
et al., 1969). Then we will report the experiments
that were conducted to evaluate its resistance to inter-
ference and the associated results. We will conclude
by explaining the interest of such a mechanism both in
neuroscience and in information processing domains.
2 MULTIPLE
ASSOCIATIVE-MEMORY
MODEL OF THE
HIPPOCAMPUS
Our hippocampal model is made up of two autoas-
sociative networks that are heteroassociatively linked
through a layer of intermediate cells (Figure 1). The
goal of this model is to store and recall specific
episodes including a perceptual part (coming from the
perception of the outer world: exteroception) and an
emotional part (coming from the perception of inter-
nal cues of different valences related to pain and plea-
sure: interoception).
The two autoassociative networks considered in
the model receive and store independently these two
types of input patterns, a
(e)
and a
(i)
. The layer of in-
termediate cells is organized into a small number of
ordered groups of valence cells that receive valence-
related information from the same interoceptive path-
ways as the interoceptive autoassociative network.
The cells in the first group can be directly activated
by interoceptive inputs to the model and can therefore
be thought of as the primary valence cells. Interocep-
tive inputs on the cells in the other groups, which are
termed associated cells, are conditional, that is, they
can not evoke postsynaptic activity within associated
cells unless a concomitant signal, m
k
, related to the
activity pattern of a precedent group is applied.
The valence cells belonging to the same group
of intermediate cells are not interconnected but in-
hibitory connections, I
i j
, exist between cells belong-
ing to different groups. The inhibitory connections
are not plastic. They are prewired such that an in-
hibitory connection from cell i to cell j exists (I
i j
=
1) if the two cells belong respectively to different
groups, k and l, and l precedes k (l < k). Thus, each
group of associated cells, once activated, silences ex-
citable cells in its preceding groups including the pri-
mary group of valence cells. This means that at most
valence cells in one group can be active at a time.
The formation of extero-interoceptive associa-
tions is done at the level of heteroassociative links,
w
(e−v)
i j
, between the exteroceptive autoassociative net-
work and the groups of intermediate valence cells.
These latter provide direct excitatory input to the inte-
roceptive autoassociative network through non-plastic
connections, w
(v−i)
i j
. These connections are prewired
only between valence cells that are sensitive to the
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
50
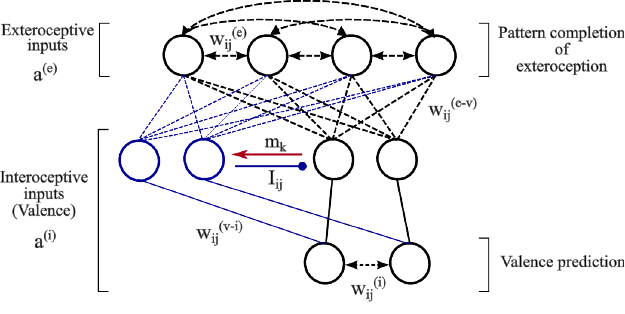
Figure 1: The architecture of the hippocampal model. Black lines denote the basic circuit of the model while blue lines denote
changes in circuitry mediated by one group of associated cells (blue) following the detection of valence-overload interference
(red arrow). Autoassociative and heteroassociative connectivities between hippocampal cells are denoted respectively by
bidirectional dashed lines and simple dashed lines without arrows. Inhibitory connections between valence cells are denoted
by lines ended with circles. Stable non-plastic connections, both excitatory and inhibitory, are denoted by solid lines.
same kind of valence.
The classical binary version of the Willshaw net-
work (Willshaw et al., 1969) is chosen as the ba-
sis for the implementation of both auto- and het-
eroassociative memory functions in the model. The
neurons are simple McCulloch-Pitts binary threshold
units and learning begins with all the synaptic weights
set to zero. Synaptic plasticity is achieved accord-
ing to a clipped version of Hebbian learning: a single
coincidence of presynaptic and postsynaptic activity
changes the synaptic weight w
i j
from 0 to 1, while
further co-activations do not induce further changes.
The recall process is done by presenting a cue pat-
tern ˜x and counting the dendritic sum for each cell j
(s
j
=
∑
n
i=1
w
i j
˜x
i
) in one-time step. The output cells
that have a dendritic sum equal to or higher than the
number of active inputs are activated. The quality of a
recalled pattern can be assessed according to its Ham-
ming distance (HD) from the originally stored pattern
(i.e. the number of elements that differ between the
two patterns. For example, if x=(0 1 1 1 0) and y=(1
1 0 1 0) then HD(x,y)=2).
Similarly to cholinergic models of the hippocam-
pus (Hasselmo et al., 1996; Meeter et al., 2004), our
model operates in transition between two modes, stor-
age and recall, depending on a hyperparameter ACh.
This mechanism is inspired from biological data de-
scribing mode switching under the dynamic regu-
lation of the levels of acetylcholine (ACh) released
from septal cholinergic projections to the hippocam-
pus. During recall, a retrieval cue, a
(e)
, is applied to
the exteroceptive autoassociative network. The pat-
tern of activity obtained at the output, ˆa
(e)
, drives re-
trieval in the heteroassociative network. An interme-
diate valence cell, l, can fire only if the dendritic sum
of its excitatory inputs exceeds the threshold value
and if it does not receive inhibitory inputs from other
valence cells that have already fired. The activity of
the intermediate valence cells, ˜a
(i)
, triggers recall in
the interoceptive autoassociative network yielding the
valence prediction by the model, ˆa
(i)
.
Just after delivery of the interoceptive informa-
tion, two novelty-detection processes take place to
compare the retrieved patterns to the actual patterns
from extero- and interoception. The novelty condi-
tion occurs when the Hamming distance between two
patterns exceeds pre-specified thresholds (HD
(e)
> e
or HD
(i)
> v). Novelty induces ACh dynamics that
favor learning of new inputs, otherwise the model set-
tles in recall mode.
During learning, excitatory intrinsic synaptic
transmission along the recurrent connections is re-
moved and activity in the model is purely driven by
afferent extero- and interoceptive inputs, a
(e)
and a
(i)
.
In the model, two kinds of interference can occur due
to a saturation, or overload of learning. The first
kind of interference occurs within the autoassocia-
tive memories when too many or too close inputs are
stored. It is called pattern overload and will not be
considered here for simplicity (we will present sparse
patterns during experiments to avoid this kind of in-
terference). The second kind of interference is called
valence overload and occurs when stimuli are simul-
taneously associated to different valences. Consider
for example learning AB+, AC- and BD-, where A,
B, C and D are exteroceptive stimuli and + and - are
interoceptive valences. Since A and B are simulta-
neously associated to + and - valences, the recall of
AB would probably generate an interference (both re-
sponses produced). The model deals with valence-
A Heteroassociative Learning Model Robust to Interference
51

Figure 2: Influence of the number of stored patterns on the accuracy of valence prediction. (A) Percentage of prediction errors
of the model without associated cells (w/o) and with associated cells after one block (W (P1)) and two blocks (W (P2)) of
training trials. (B,C) Details of the simulation results when the block size is set to 100. B: Rates of interference detection
during the first (T1) and second (T2) training trials. C: Number of groups of associated cells needed to resolve interference
detected during training trials T1 and T2.
Figure 3: Performance of the proposed model after training on 100 input patterns. The model is tested using partial cues in
which 1, 2, or 3 out of 6 active elements in the original inputs are turned off. (A) Pattern completion performance, defined
as the percentage of retrieved patterns that differ at least by one element from the originally stored patterns. (B) Pattern
completion performance, defined in terms of Hamming distance between the stored and retrieved patterns. (C, D) Valence
prediction performance of the proposed model with (w) and without (w/o) associated cells after one and two blocks of
training trials. (E) Maximal number of groups of associated cells needed to resolve interference detected under all simulation
conditions (one and two blocks of training trials P1 and P2, and for 1/6, 2/6 and 3/6 partial-cue conditions).
overload interference by monitoring activity of in-
termediate valence cells, y
(v)
. If any activity is ob-
served among intermediate valence cells (
∑
i
y
(v)
i
> 0)
in response to exteroceptive inputs a matching pro-
cess takes place to determine whether this activity
matches interoceptive valence-specific inputs. A mis-
match (HD
(v)
> v) signals a potential interference to
a successive group of associated valence cells that be-
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
52

Figure 4: Discrimination reversal learning. (A) Percentage of prediction errors of the model with (w) and without (w/o)
associated cells. (B) Rates of interference detection over each block of trials. (C) Number of groups of associated cells
needed to resolve interference across the different blocks of trials.
come able to respond to valence-related inputs and
rapidly silence valence cells that were active in pre-
ceding groups.
3 EXPERIMENTS
The validity of the proposed model is examined
through a series of numerical experiments (cf.
(Kassab and Alexandre, 2015) for the description of
other numerical experiments with this model). The
simulated model is configured with 150 cells in the
exteroceptive autoassociative network and 3 cells in
the interoceptive autoassociative network. The inter-
mediate valence cells are organized into 5 groups of 3
cells each.
Inputs are provided to the model as two indepen-
dent patterns of activity. The exteroceptive inputs
are generated as random 150-element binary patterns
with 6 elements being active (set to 1). The interocep-
tive inputs are modeled by 3 binary cells to differenti-
ate positive, negative and neutral valence states. One
of these cells switches to its active state according to
whether a pleasant (100), unpleasant (010), or neutral
(001) stimulus is present.
The performance is evaluated by comparing the
output patterns recalled by the model against the orig-
inal representation of the input patterns that were
A Heteroassociative Learning Model Robust to Interference
53
given as new information to be stored in the model.
Specifically, two kinds of recall errors are considered
when evaluating simulation results. Pattern comple-
tion errors which reflect the Hamming distance be-
tween the learned and retrieved activation for extero-
ceptive patterns, and valence prediction errors which
reflect the Hamming distance between the correct and
predicted valence. In both cases, errors are scored
when Hamming distance is greater than zero.
Two types of simulations are set out to test the
model for its ability to rapidly link exteroceptive pat-
terns and their emotional valences while avoiding va-
lence overload interference. The first set of simu-
lations examines the effect of the number of stored
patterns on the accuracy of valence prediction. The
model is tested under full-cue and partial-cue re-
call conditions. In both cases the performance of
the proposed model is compared with that of a re-
duced model with the groups of associated cells re-
moved. The second set of simulations focuses on how
to quantify the ability of associated valence units to
orthogonalize conflicting associations arising from a
change in previously learned valence values. In all
simulations, we assume that the representations of in-
put patterns are sufficiently pulled apart so that no
interference can occur at the level of autoassociative
memories (no pattern overload). This is important to
ensure that the effects observed in the model stem di-
rectly from valence overload interference at the level
of heteroassociative links between exteroceptive and
interoceptive patterns. All results are averaged over
5 simulation runs and are displayed throughout the
figures as mean ± standard error of the mean. The
novelty-detection thresholds, e and v, are set to zero
for all the simulations.
4 RESULTS
4.1 Overloading
The first set of simulations is run by varying the num-
ber of training patterns and observing how valence
prediction is affected with and without the groups
of associated cells included in the model (Figure 2).
Training patterns are presented randomly into blocks
of N trials. Following the first presentation of training
patterns, the prediction of the full and reduced mod-
els is perfect up to N=20, after which point prediction
errors begin to occur more frequently with increasing
size of the blocks of training trials. At N=100, the
percentage of prediction errors is a little more than
30% for the reduced model but falls to about 17% for
the full model. This reduction results from the identi-
fication of about 8% of the stored associations as in-
terfering associations (Figure 2B). Interference effect
is accordingly reduced through the recruitment of one
group of associated cells (Figure 2C). During the sec-
ond presentation of training patterns, the full model
detects all the interfering associations that remain and
orthogonalizes them using the same group of asso-
ciated cells (Figure 2C). Therefore, the performance
of valence prediction differs significantly between the
two models after the second presentation of training
patterns: the reduced model continues to commit the
same prediction errors while the proposed model per-
forms with no errors at all.
Next, the model is trained in the same manner as
in the previous simulations except that recall is trig-
gered by partial versions of the original trained pat-
terns. Specifically, the block size is set to 100 training
patterns and the model is cued with partial versions
with either 1, 2 or 3 of the 6 active inputs turned
off. Figures 3C and D show that the accuracy of
valence prediction with the 1/6 partial-cue condition
is the same as that obtained with the full-cue condi-
tion. This is because exteroceptive patterns are al-
most perfectly reconstructed as shown in Figures 3A
and B. The removal of two or three of the six active
cues causes a proportional decrease in the accuracy
of pattern completion of exteroceptive patterns. Con-
sequently, the improvement in valence prediction by
the proposed model is less pronounced but still highly
significant as compared to the reduced model. For
all percentages of removal tested, the model makes
use of one group of associated cells to tackle valence-
overload interference (Figure 3E).
4.2 Discrimination and Reversal
Here we investigate the functional significance of the
groups of associated cells using numerical simula-
tions with reversal learning tasks. The task in the
first set of simulations involves two phases. In the
first phase the model is presented repeatedly with 50
training patterns [e.g. A+, B-, C (neutral), etc.] over
4 blocks of trials and the percentage of prediction er-
rors made at the beginning of each trial is measured
and displayed in Figure 4A. This is a simple discrim-
ination learning problem similar to those tested in
the previous simulations. Thus as was observed be-
fore, valence-overload interference occurs at the early
stages of learning and exhibits the recruitment of one
group of associated cells to tackle it. When the groups
of associated cells are removed the reduced model
shows impaired performance that persists over the re-
peated trials. In the second phase, emotional valences
of the training patterns are randomly changed to other
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
54

Table 1: The experimental design of the task of (Levy-Gigi et al., 2011). Note. A–H refer to eight cue shapes, 1–8, eight
contexts, + and – indicate respectively positive and negative valences.
Training patterns Task
Group 1 Group 2 Group 3 Phase 1 Phase 2
(original) (cue reversal) (context reversal) (acquisition) (retention & reversal)
A1+ E1– A5– Group1 Group1
B2+ F2– B6– Group2
C3– G3+ C7+ Group3
D4– H4+ D8+
value with a probability of 50% [e.g. A-, B (neutral),
C (neutral), etc.]. As shown in Figure 4A the pro-
posed model quickly learns to reverse its behavior as
all the emotionally changed patterns are detected and
learned on the first training trials after reversal. On
the other hand, the reduced model fails to acquire the
new associations since the old ones have not been un-
learned.
The second set of simulations involves a cue-
context reversal learning task similar to that estab-
lished by (Levy-Gigi et al., 2011) to investigate rever-
sal learning in patients with mild amnesic cognitive
impairment. To simulate this task, three groups of 4
exteroceptive patterns each are formed such that one
of the 6 active elements is used to encode the presence
of a sensory cue and the others to encode contextual
cues. No overlap is allowed between cells encoding
for different cues or contexts (cf. Table 1).
In the first phase of acquisition, the model is re-
peatedly presented with the training patterns in the
first group and valence prediction is evaluated over
four blocks of training trials. Figure 5 shows that both
full and reduced models make correct valence predic-
tion after a single exposure to the training patterns.
Then, the reversal phase is immediately followed by
exposing the models to new training patterns from the
second and third groups, in addition to the old ones.
The training patterns are also presented repeatedly
four times in random order. The results show that,
in the first block of trials, valence prediction errors
are made for both new and old patterns. This reflects
the fact that heteroassociative connections are irrele-
vantly strengthened between the original patterns and
valences of new patterns. When interference is de-
tected, one group of valence-associated cells is re-
cruited and prediction errors fall to zero rapidly on
the third block of trials after reversal. In contrast, the
number of prediction errors the reduced model makes
is still the same as the blocks progress for the same
reason stated above.
5 DISCUSSION
This paper sets emphasis on a class of connectionist
models, associative memories, with powerful proper-
ties for learning by heart specific patterns and recall-
ing them from partial information. Such models can
be simply used for pattern retrieval but also in het-
eroassociation between two classes of inputs. In our
biologically informed model (Kassab and Alexandre,
2015), we propose such a heteroassociation between
exteroception and interoception. From an informa-
tion processing point of view, we explain in that pa-
per that a heteroassociation between two data spaces
of different size leads to more robust retrieval than a
simple autoassociation with a flat vector concatenat-
ing both kinds of information because the evaluation
of the Hamming distance between stored and actual
patterns would consider in this latter case that one er-
ror in any dimension yields the same penalty, which is
obviously not the case. Beyond the case for pavlovian
conditioning with intero- and exteroceptive cues, we
believe that it is not rare in the information processing
domain to cope with such associations between data
of different dimensions, as it is the case for example
with labeled data (high-dimensional data associated
with a symbolic label). In this case, we claim that
combining auto- and heteroassociation as proposed
here results in more robustness in the retrieval phase.
Results reported in the present paper were cen-
tered on another powerful property of our model,
for managing interferences. When an association is
learned between a high dimensional data space and
a smaller space representing labels (valences in the
present case), one central problem is about the as-
sociation of close patterns with different labels or of
different combinations of patterns with different la-
bels. This classical problem has been termed config-
ural learning (Buhusi and Schmajuk, 1996). Based
on biological data and also benefiting from the sepa-
ration between exteroceptive and interoceptive data,
we have proposed in the present model a mecha-
A Heteroassociative Learning Model Robust to Interference
55

Figure 5: Cue-context reversal learning. (A) Percentage of prediction errors of the model with (w) and without (w/o) associ-
ated cells. (B) Rates of interference detection over each block of trials. (C) Number of groups of associated cells needed to
resolve interference across the different blocks of trials.
nism able to automatically detect such interference at
the heteroassociative level and to trigger new learn-
ing accordingly. The experiments reported here show
that our model is very efficient at performing such
a learning. In addition, this learning process is very
quick, which preserves another important specificity
of episodic learning.
These results have been described here in the
framework of information processing, but one of the
experiments has also been designed to reproduce be-
havioral and cognitive data in the medical domain for
amnesic impairments (Levy-Gigi et al., 2011). Re-
lated medical data strongly suggest the central role of
the hippocampus in this memory process, giving ad-
ditional interest to the complementary learning sys-
tem hypothesis (O’Reilly et al., 2011). This cognitive
framework also postulates how procedural learning in
the cortex, slowly learning and able of generalization,
might be instructed by specific cases learned quickly
in the hippocampus avoiding interferences. Coming
back to the information processing domain, we be-
lieve that better understanding these processes and
modeling them more faithfully is of high interest for
designing machine learning systems combining dif-
ferent memory processes for higher performances.
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
56
REFERENCES
Buhusi, C. V. and Schmajuk, N. A. (1996). Attention, con-
figuration, and hippocampal function. Hippocampus,
6(6):621–642.
Carrere, M. and Alexandre, F. (2015). A pavlovian model of
the amygdala and its influence within the medial tem-
poral lobe. Frontiers in Systems Neuroscience, 9(41).
Graham, B. and Willshaw, D. (1997). Capacity and in-
formation efficiency of the associative net. Network:
Computation in Neural Systems, 8(1):35–54.
Hasselmo, M. E., Wyble, B. P., and Wallenstein, G. V.
(1996). Encoding and retrieval of episodic memories:
Role of cholinergic and gabaergic modulation in the
hippocampus. Hippocampus, 6(6):693–708.
Hopfield, J. J. (1982). Neural networks and physical sys-
tems with emergent collective computational abilities.
In Proceedings of the National Academy of Sciences,
USA, pages 2554–2558.
Kassab, R. and Alexandre, F. (2015). Integration of extero-
ceptive and interoceptive information within the hip-
pocampus: a computational study. Frontiers in Sys-
tems Neuroscience, 9(87).
Knoblauch, A., Palm, G., and Sommer, F. T. (2010). Mem-
ory capacities for synaptic and structural plasticity.
Neural Computation, 22(2):289–341.
Levy-Gigi, E., Kelemen, O., Gluck, M. A., and K
´
eri, S.
(2011). Impaired context reversal learning, but not cue
reversal learning, in patients with amnestic mild cog-
nitive impairment. Neuropsychologia, 49(12):3320–6.
McClelland, J. L., McNaughton, B. L., and O’Reilly, R. C.
(1995). Why there are complementary learning sys-
tems in the hippocampus and neocortex: insights
from the successes and failures of connectionist mod-
els of learning and memory. Psychological review,
102(3):419–457.
McNaughton, B. and Nadel, L. (1990). Hebb-marr net-
works and the neurobiological representation of action
in space. In Neuroscience and Connectionist Theory,
pages 1–63. Hillsdale, NJ: L. Erlbaum.
Meeter, M., Murre, J. M., and Talamini, L. M. (2004). Mode
shifting between storage and recall based on novelty
detection in oscillating hippocampal circuits. Hip-
pocampus, 14(6):722–41.
O’Reilly, R. C., Bhattacharyya, R., Howard, M. D., and
Ketz, N. (2011). Complementary Learning Systems.
Cognitive Science.
Samura, T., Hattori, M., and Ishizaki, S. (2008). Se-
quence disambiguation and pattern completion by co-
operation between autoassociative and heteroassocia-
tive memories of functionally divided hippocampal
CA3. Neurocomputing, 71(16–18):3176–183.
Tulving, E. (1972). Episodic and semantic memory. Orga-
nization of Memory. Academic Press.
Willshaw, D. J., Buneman, O. P., and Longuet-Higgins,
H. C. (1969). Non-holographic associative memory.
Nature, 222(5197):960–962.
A Heteroassociative Learning Model Robust to Interference
57
