Calculation of Running Economy with a Biomechanical Model versus
Indirect Calorimetry
Lennart Gullstrand
1,2
, Daniele Cardinale
1,3
and Johnny Nilsson
3,4
1
Elite Sports Centre, Swedish Sports Confederation, Bosön, Lidingö, Sweden
2
Section of Exercise Physiology, Dept. of Physiology and Pharmacology, Karolinska Institutet, Stockholm, Sweden
3
Dept. of Sport and Health Science, The Swedish School of Health and Sports Sciences, Stockholm, Sweden
4
University of Dalarna, Falun, Sweden
1 OBJECTIVES
The interest in running economy (RE) analysis, based
on metabolic and biomechanical measurements, has
increased during the last decades. In this study a new
“body marker-free” (BMF) method (MotionMetrix
Inc., Stockholm, Sweden), based on two depth
sensitive cameras was used to capture the runners
motion during treadmill running. A 3D segment
model was generated and after kinematic and kinetic
analysis a number of running parameters were
derived. Running economy is originally defined as
the metabolic cost from measurement of oxygen
uptake (VO
2
) in mL·kg
-1
·min
-1
at submaximal and
steady state velocities (Costill et al., 1970) and is here
compared to energy expenditure (EE) in J·kg
-1
·min
-1
,
derived from the new biomechanical model (BM).
2 METHODS
Seven well trained middle- and long distance runners,
with an average mass and height of 68.7 ± 3.9 kg and
187.7 ± 5.2 cm, respectively and a VO
2
max of 67.8
± 5.1 mL· kg
-1
· min
-1
, volunteered in the study
according to the Helsinki Declaration. Four
submaximal (12, 14, 16 and 18 km·h
-1
) speeds were
performed on a high precision treadmill. VO
2
was
measured with a validated metabolic chart
(OxyconPro, CareFusion GmbH, Germany) in the
mixing chamber mode. Simultaneously the motions
were captured with the new BMF method. The new
biomechanical model used body segments
movements which were calculated to represent one
whole centre of mass movement (Willems et al.,
1994, Cavagna and Kaneko, 1977).
3 RESULTS
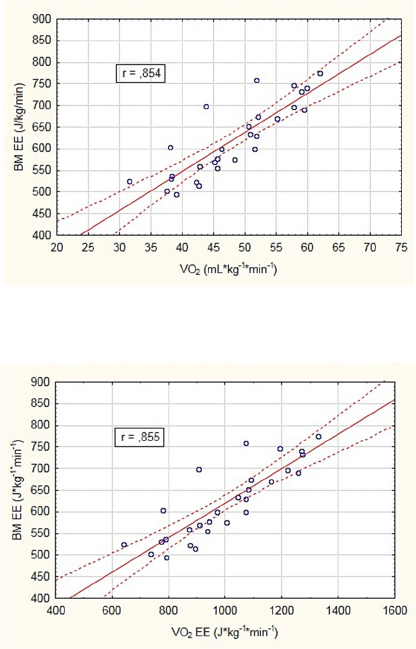
The correlation coefficient calculated between VO
2
related to body mass (mL· kg
-1
· min
-1
and mL·kg
-
0.75
·min
-1
) and BM EE were 0.854 and 0.856,
respectively and were significant (Figure 1). When
the biomechanical rate of energy expenditure was
related to VO
2
expressed in L·min
-1
the correlation
coefficient was still high with a significant p-value of
0.834. Furthermore, using the OxyconPro software to
get EE (kcal·day
-1
) from VO
2
and calculated to J·kg
-
1
·min
-1
, based on the de Weir formula (de Weir,
1949), resulted in a similar correlation. Even though
a strong correlation was found, the EE values derived
from the 2 methods differed 20-40 % (Coefficient of
Variation 7.8%) and were related to both individual
athletes as well as running speeds (Figure 2).
4 DISCUSSION
To calculate RE by means of biomechanical variables
with the BMF method is of great interest. This
method allows evaluation of RE without manual
attaching of body markers and using expensive
respiratory equipment. Thus the participants are not
connected to any measurement device that may be
related to restrictions in running. In addition,
interesting data for evaluating RE such as stride rate,
stride length, foot contact time and vertical
displacement can be obtained. These are possible
biomechanical factors influencing the RE.
Unexpectedly, specifically the centre of mass (CoM)
vertical displacement (V
disp
) data in this investigation
showed a low, not significant correlation to VO
2
-
derived RE. CoM V
disp
is in the literature regarded as
one of the more important sub factors influencing the
running economy (Williams and Cavanagh, 1987).
Nevertheless, the BM EE and VO
2
values showed a
strong correlation.
Gullstrand, L., Cardinale, D. and Nilsson, J..
Calculation of Running Economy with a Biomechanical Model versus Indirect Calorimetry.
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

When translating EE from VO
2
data and comparing
to the BM calculated EE, although strongly
correlated, we found significant differences ranging
from 20-40%. There may be several biomechanical
reasons for this discrepancy. For example, it is
unknown if the model accounts for stored elastic
energy in stretch-shortening cycle components,
which would add to the BM EE and reduce the
difference.
However promising, we intend to further validate
the actual method against a more sophisticated
optoelectronic set up with multi joint reflectors,
which may be regarded as a biomechanical gold
standard.
4.1 Figures
Figure 1: BM calculated EE compared to VO
2
during
running at 12, 14, 16 and 18 km·h
-1
.
Figure 2: BM calculated EE compared to VO
2
based EE
during running at 12, 14, 16 and 18 km·h
-1
.
REFERENCES
Costill, D., Winrow, E., 1970. A comparison of two middle-
aged ultra-marathon runners. Res. Q., 41:135-139.
Cavagna, GA., Kaneko, M. Mechanical work and efficiency
in level walking and running. 1977. J. Physiol,, 268,
467-481
Willems, PA., Cavagna GA., Heglund, NC., 1994.
External, internal and total work in human locomotion.
J. Exp. Biol., 198, 379-393.
De Weir, JB., 1949. New methods for calculating metabolic
rate with special reference to protein metabolism. J.
Physiol. 109, 1-9.
Williams KR & Cavanagh PR. Relationship between
distance running mechanics, running economy and
performance. J. Appl. Physiol. 1987: 63(3): 1236-47