Semantic Spatial Reasoning
Developing a Conceptual Framework for Reasoning with Semantic,
Qualitative-Quantitative Spatial Information
Roman Katerinenko
Oracle Labs, Schiffbauergasse 14, Potsdam, Germany
Keywords:
Qualitative Spatial Reasoning, Rule-based Reasoning, CDC, RCC-8, RDF, Semantic Web, OWL.
Abstract:
In recent years, significant achievements have been made on handling qualitative spatial relations in the field
of qualitative spatial reasoning. These achievements can be utilized to bridge the gap between geometries and
semantics of real-world objects. With this purpose we introduce the Semantic Spatial Reasoning conceptual
framework for reasoning with information of mixed types: qualitative-quantitative spatial and information
described with the help of the Semantic Web technologies. The objective of this framework is not to be a
particular reasoning algorithm but a conceptual decomposition suitable for showing benefits of the combined
reasoning approach, forecasting practical applications and giving a clue for an implementation. Modular
structure of the framework makes it useful to model various tasks in areas, such as, GIS, cognitive vision,
computer-aided design, data integration.
1 INTRODUCTION
In recent years, significant achievements have been
made on handling qualitative spatial (QS) relations in
the field of qualitative spatial reasoning (QSR). QS
relations are symbol abstractions of geometric repre-
sentations which allow to use qualitative terms to for-
mulate rules in order to describe spatial situations and
actions. Normally, systems dealing with spatial in-
formation also capture it’s semantics. Therefore, we
decided to extend QSR with ability to reason with
semantic information and introduced Semantic Spa-
tial Reasoning (SSR) conceptual framework. In our
investigation, we concluded that the abilities of our
approach broader than often-considered constraint-
based reasoning abilities of QSR because it allows to
generate new spatially-enabled knowledge from ex-
isting knowledge.
Research in the field of QSR have been conducted
in different directions, such as, design of and rea-
soning with QS calculi, their combination (De Fe-
lice, 2013) and effective implementation (Schneider,
2002). A wide variety of QS calculi has been de-
veloped to model different aspects of the space like
topology (Region Connection Calculus, RCC-8), car-
dinal directions (Cardinal Directions Calculi, CDC),
relative orientation, distance, visibility, shape, size.
Herewith, there was a relatively small investigation
of using the Semantic Web technologies in combina-
tion with QSR, mostly related to the improvement of
quantification with the help of rules (De Felice, 2013).
From the opposite side, there are some efforts
to develop spatial extensions of some Semantic Web
technologies like GeoRDF and GeoSPARQL (Perry
and Herring, 2012) but, regarding incorporation of
QSR into this standards, only topology calculus
(RCC-8) were added. Therefore, our goal is to bridge
this gap by the development of SSR.
In this article we introduce a conceptual frame-
work for SSR which allows reasoning with differ-
ent types of information — semantic, qualitative-
quantitative spatial. The objective of this framework
is not to be a particular reasoning algorithm but a
conceptual decomposition suitable for showing ben-
efits of the combined reasoning approach, forecasting
practical applications and giving a clue for an imple-
mentation.
2 BASIC ELEMENTS
Coad and Yourdon (Coad and Yourdon, 1991) con-
cluded that it is natural for human to use the object-
oriented approach for thinking about real world: dif-
ferentiation of experience into particular objects, dis-
Katerinenko, R..
Semantic Spatial Reasoning - Developing a Conceptual Framework for Reasoning with Semantic, Qualitative-Quantitative Spatial Information.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 2: KEOD, pages 257-262
ISBN: 978-989-758-158-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
257

tinction between the whole object and it’s part and
distinction between different classes of objects. The
Semantic Web technologies like RDF and OWL have
successfully utilized this approach and added a very
important concept of a relation which is used to re-
flect arbitrary dependencies between real-world ob-
jects. When considering objects having spatial extent
(spatial objects) qualitative spatial (QS) relations are
normally used to handle information which can in-
clude concepts, such as, “inside”, “next-to”, “part-of”
rather than geometrically specific data with numerical
coordinates. These relations are studied in the field of
Artificial Intelligence called Qualitative Spatial Rea-
soning (QSR). So we can conclude that QSR and the
Semantic Web technologies have a common ground
— object-oriented approach, thus it is a natural thing
to investigate possibilities of the combined approach
which we call Semantic Spatial Reasoning (SSR).
With a view to be semantically close to the object–
oriented approach, we have included the following
basic concepts to our model: objects, classes, prop-
erties of objects and relations between them. We dis-
tinguish two types of objects: the objects with known
spatial extent (SE) and others. In the remainder of
this article we refer to the former objects as O
s
and
to the latter as O. In the same way we distinguish
two types of relations: QS relations and others which
we call semantic relations for simplicity. QS relation
(R
s
) could be an arbitrary relation of any QS calculi,
such as, CDC, RCC-8 or OPRA. Semantic relations
(R
sem
) express some other relations between objects,
such as, administrative (“report-to”), family (“parent-
of”), friendship (“who-likes-whom”), etc. Such dis-
tinction to spatial and not spatial elements allows us to
analyze possible translation (mapping) functions be-
tween O
s
, O, R
s
, R
sem
in the next section.
3 TRANSLATION OPERATIONS
In this section we introduce the next part of our con-
ceptual framework — translation operations which
perform translation or mapping between different
types of the basic elements. We have analyzed all
possible translation operations between objects, ob-
jects with SE, QS relations, semantic relations and
have selected six meaningful. The quantification (see
Section 3.2) and qualification (see Section 3.3) opera-
tions have been studied in literature but the others are
our own contribution.
3.1 Translation Operations Sem, Geom
The Sem translation operation is supposed to define
semantics for an object, so that this semantics could
be used in the rule-based reasoning described in Sec-
tion 4.2. In the Semantic Web technologies semantics
of a real-world object is captured within it’s relations
to another objects. For example, given object’s identi-
fier as an input, the Sem operation could yield the se-
mantic network containing information about object’s
class, properties and relations. Sometimes such se-
mantic information is contained in geographic maps
as a“thematic layer” or, in case of OpenStreetMaps,
is contained in “tags” attached to objects.
The Geom translation operation yields object’s SE
which is used in the QS reasoning and the transla-
tion operations. The result could be a vector geometry
stored in a spatial database or a text description kept
in GeoRDF and turned to a vector geometry.
3.2 Quantification
The quantification operation was defined in (Wolter
and Wallgr¨un, 2012) as the process of computing a ge-
ometric interpretation of a qualitative relation consid-
ering geometries of the reference objects. The com-
putation is based on the geometric semantics of the
relation. For most qualitative calculi quantification
hasn’t been studied yet, but for CDC and RCC-8 it
can be implemented relatively simple.
We have extended this notion to use with objects
and several calculi simultaneously: the quantification
operation approximates a possible SE of O
∗
(with as-
terisk we mark objects with unknown SE) by quanti-
fying all QS relations R
s
(O
∗
, O
s
1
, . . . , O
s
n
) associated
with it. More precisely the quantification of O
∗
is
computation of a spatial region that the real-world
entity represented by O
∗
can occupy in order to sat-
isfy all QS relations R
s
(O
∗
, O
s
1
, . . . , O
s
n
) with respect
to the reference objects O
s
1
, . . . , O
s
n
. The quantifica-
tion is impossible when SE for all reference objects
are unknown. As a result O
∗
gets not just an exem-
plar region which satisfies the relations but the max-
imum region which is union of all possible exemplar
regions.
A
B
C
D
east,
externally connected
south-west
west
east
south-east
N
E
W
S
A
B
C
D
Figure 1: Constraint network for the geometric scene.
KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development
258
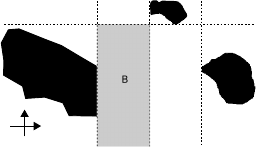
For example, if it was required to quantify object
B shown in Figure 1 then the quantification operation
could compute the region shown in Figure 2. Obvi-
ously, the quantified region is less precise than the
real-world object, but the more objects and relations
are involved the more precise the result is. In our nota-
A
B
C
D
N
E
W
S
Figure 2: Quantification of object B.
tion the quantification operation expressed as follows:
Quantification : O
∗
, R
s
(O
∗
, O
s
1
, . . . , O
s
n
) 7→ O
s
3.3 Qualification
The opposite to the quantification operation is the
qualification operation. It yields the QS relation
which holds between objects with SE:
Qualification : O
s
1
, . . . , O
s
n
7→ R
s
(O
s
1
, . . . , O
s
n
)
Given that the system contains several calculi, the
quantification operation requires to check the con-
straints which every calculus defines for the objects
in a all relations. For example, to qualify a relation
in the system containing RCC-8 and CDC calculi the
quantification requires to check whether the objects
overlap, disjoint, one object is located to the north of
another, etc.
3.4 Translation Operations TO
1
, TO
2
Previously, we have considered four elements of our
framework: objects in general, objects with known
SE, QS relations and translation operations between
them (quantification, qualification). Now we are
adding the rest part of our model — semantic objects,
rules, relations and considering possible translation
operations between whole elements of the model.
At first, we consider the mapping between an arbi-
trary semantic relation and a QS relation for the same
objects: R
s
(O
1
, . . . , O
n
) ↔ R
sem
(O
1
, . . . , O
n
). The Se-
mantic Web technologies allows to define any ar-
bitrary relation but we do think the restriction for
this translation operation is those semantic relations
which have synonymic QS relations. For example,
one could define an RDF relations, such as, “next-
to”,“close-to”, “near” which, could be mapped to the
“externally connected” RCC-8 relation. So CDC re-
lations, such as,“north”, “east” could be mapped to
the “in-front-of” and “to-the-right” RDF relations. In
other words, this translation operation allows to uti-
lize QS relations during the rule-based reasoning and
utilize semantic relations during the QS reasoning.
For more thorough analysis we divide this transla-
tion operation into two separate operations (TO):
TO
1
: R
s
(O
1
, . . . , O
n
) 7→ R
sem
(O
1
, . . . , O
n
)
TO
2
: R
sem
(O
1
, . . . , O
n
) 7→ R
s
(O
1
, . . . , O
n
)
In general, TO
1
should be treated not just as a
mapping but as the operation which defines semantics
of an object taking into account it’s QS relations with
another objects. An exemplar implementation could
accept inputs as: a geometric scene; QS relations be-
tween the objects of the scene; geographic or admin-
istrative semantics for some of them, such as, “build-
ing”, “bridge”, “river”; etc. Afterwards, TO
1
yields
a semantic description of the scene, such as, “An un-
known object O
∗
is connected to particular road and
overlaps particular river” but in the form of a seman-
tic network. This semantic network could be turned
into a SPARQL query to search the RDF concept for
O
∗
in some RDF graph. This RDF concept could be
treated as semantics of O
∗
.
We admit that some geographic feature recogni-
tion or image analysis algorithms could do this job as
well and decide that O
∗
is likely a “bridge”, but our
approach could find the name of the bridge if the RDF
graph is detailed enough. Also probabilistic machine
learning models could be utilized for TO
1
implemen-
tation.
Considering TO
2
, there are two cases. In case
when all SEs of O
1
, . . . , O
n
are known, TO
2
is just
a mapping between synonymic relations . In case,
there is an object O
∗
with unknown SE this operation
(in combination with quantification) could determine
it. As an exemplar scenario, let us consider the fol-
lowing news message: “Undefined object is between
the church and the railroad and close to the bus stop”.
This information could be captured as an RDF graph.
Moreover, SE of the church, the railroad and the bus
stop are known from the map of the city. So after-
wards, TO
2
yields constraint network (similar to the
one shown in Figure 1) consisting of QS relations and
one object with unknown SE, which could be com-
puted later by the quantification operation.
Mentioned scenario is related to the task of com-
putation of quantitative spatial scene by it’s text, video
or speech description. In general, the result geometry
is not a perfect match with the real-world geometry of
the object but this approximations is especially useful
in case of observations when precise coordinates of
the observable object are not available or not needed,
such as, “crowd movement” observation.
Semantic Spatial Reasoning - Developing a Conceptual Framework for Reasoning with Semantic, Qualitative-Quantitative Spatial
Information
259

Comparing to a conventional quantification, the
combination of Sem, TO
2
and quantification can
achieve a better result and compute SE more precisely
because it is possible to utilize semantic information
about object’s geometry, such as, shape or size. In
our framework this information could be kept in the
class of an object. For example, the information that
the target object is instance of a car-like shape class
could be accounted during the quantification process.
We think that investigation of this possibility is related
to the idea of using real algebraic geometry for the
quantification suggested here (Wolter and Wallgr¨un,
2012).
3.5 Translation Operations TO
3
, TO
4
These two translation operations are different from
the others because their purpose is to produce new
objects. Introduction of new objects during reasoning
process is not a typical situation for a reasoner. For
instance, Semantic Web reasoners are supposed to in-
troduce new relations between entities, but not new
entities. Datalog-style reasoners are the same. But,
sometimes, such feature is needed for the application
purposes. So that Oracle Database supports this fea-
ture in combination with user-defined rule reasoning.
In our notation TO
3
, TO
4
are expressed as fol-
lows:
TO
3
: R
sem
(O
s
1
, . . . , O
s
n
) 7→ O
s
TO
4
: R
s
(O
s
1
, . . . , O
s
n
) 7→ O
s
The idea of both operations is the same, but TO
3
is designed to compose a new object by semantic re-
lations while TO
4
accepts QS relations. New object
is the result of application of geometric operations to
O
s
1
, . . . , O
s
n
input objects with known SE. The geomet-
ric operations could be of any kind, such as, compu-
tation of union, difference, convex hull, etc.
For example, in a particular application TO
4
could
be implemented in the following way: if O
s
1
is a
“house”, O
s
2
is a “garden” and R
s
is “externally-
connected” RCC-8 relation between O
s
1
and O
s
2
then
TO
4
yields new object O
s
“household” which SE is
geometric union of O
s
1
and O
s
2
regions.
4 SEMANTIC SPATIAL
REASONER
In this section we introduce architecture of the seman-
tic spatial reasoner. We have developed it with the
aim to show great possibilities of combined reasoning
process utilizing the translation operations described
in Section 3.The reasoner (see Figure 3) consists of
two major modules: QSR and rule-based reasoner.
They run in a loop until fixpoint state is reached and
no new information can be inferred anymore.
Rulebase
Figure 3: Semantic spatial reasoner architecture.
4.1 Qualitative Spatial Reasoner
This module was introduced in (De Felice, 2013) as a
system for integration of quantitative and QS infor-
mation. For this purpose it contains three compo-
nents: qualification, quantification components and
qualitative reasoner. We have added QS reasoner to
our framework in it’s original meaning but with one
extension — we added ability to influence the quan-
tification component by semantic rules. The reason
for that will be discussed in Section 4.3.
All three components operate on the same data
structure — the constraint network in which the edges
are labeled with relations from QS calculi; the nodes
correspond to the objects with known or unknown SE.
The quantification component applies the quantifica-
tion operations (see Section 3.2) to every object with
unknown SE in order to find it’s possible geometry
with respect to the constraints (relations). Afterwards,
the qualification component applies qualification op-
eration (see Section 3.3) to every object in order to
deduce it’s QS relations with the others. The next turn
is for qualitative reasoner which is based on algebraic
closure or path consistency algorithm (Mackworth,
1977) that applies composition and permutation op-
erations defined in a calculus to propagate the con-
straints through the network and infer as much newre-
lations as possible. Main loop continues while infor-
mation in the constraint network is changing. When
fixpoint is reached the rule-based reasoner steps into
the reasoning process.
KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development
260

4.2 Rule based Reasoner
By the rule-based reasoner we mean a reasoner which
applies rules to some informationand deduces newin-
formation complied with the rules. This type of rea-
soning is known as a forward chaining inference or
bottom-up inference. Such reasoning process finishes
at a fixpoint state. A rule is an IF — THEN construc-
tion. If some condition (the IF part) that is checkable
in some dataset holds, then the conclusion (the THEN
part) is processed.
There are many types of rules with different syn-
tax and semantics. In our framework we are us-
ing the Datalog-style rules (Katerinenko and Bess-
mertnyi, 2011). Such rules contain relations in both
parts. For example, the fact that a car is parked
in a parking might be expressed with relation like
parkedIn(car, parking). Adding the notion of vari-
ables, a rule could be something like:
IFparkedIn(?x, ?y)THENntpp(?x, ?y)
where “ntpp” stands for “non-tangential-proper-part”
RCC-8 relation. It is expected that for every pair
of ?x and ?y for which parkedIn relation holds, the
rule-based reasoner can conclude that the ntpp re-
lation holds as well and the corresponding relation
ntpp(car, parking) is added to the dataset.
4.3 Rules as Constraints
Qualitative representations enable capturing concep-
tual knowledge while abstracting of complexity of
real-world numeric information. Thus, it is a natu-
ral choice to use QS reasoning in conjunction with
rule-based reasoning. But there is another possibil-
ity for cooperation — rules can be used as constraints
to guide quantification. For example, it is possible to
compose a rule from the statement “A river can not
intersect a house” and use this rule during computa-
tion of SE for the house. This idea was presented in
(De Felice, 2013) as additional to QS reasoner “the-
matic reduction” component, but in our case it is an
integral part of the framework. Thus, the same rule-
base could be used for this purpose and for rule-based
reasoning.
5 COMBINED REASONING
WITH THE TRANSLATION
OPERATIONS
In this section we demonstrate how the translation op-
erations enable mutually compliment reasoning. Let
us consider an exemplar dataset of mixed information
in order to demonstrate one iteration of the semantic
spatial reasoner. For the simplicity we are consider-
ing dataset which has been converted to the form of
a constraint network briefly discussed in Section 4.1.
This network is shown in Figure 4, in which black
circle nodes represent objects, square nodes represent
objects with known SE, straight line edges represent
QS relations and dashed edges represent semantic re-
lations. For simplicity, we have omitted directions on
the edges and considering only binary relations. Also
let’s assume that this network is the result of the first
application of the QS reasoner to the dataset. For de-
tails of this process refer to (De Felice, 2013).
As it is expected, after QS reasoning all objects
which have at least one relation with the object with
known SE were quantified. Otherwise, the quantifica-
tion operation are not able to compute geometry for
it, like in case with triangular subnetwork in the left
part (see Figure 4). The same way, all QS relations
between objects with known SE were found. Ap-
plication of the TO
1
, TO
2
translation operations have
added two new edges E
2
, E
3
to the network (see Fig-
ure 5). The E
1
edge represents a QS relation appeared
after application of TO
2
to the semantic relation of
the E
1
edge. Now E
2
is adjacent to the object with
known SE that means that SE for the second adjacent
object will be found on the next invocation of the QS
reasoner. In contrast to the E
2
, edge E
3
appeared after
application of TO
1
to the corresponding QS relation.
Figure 4: Exemplar constraint network.
E
1
E
2
E
3
Figure 5: The network after TO
1
, TO
2
application.
The next modifications are done by the Sem and
Geom operations as shown in Figure 6. Geom has
found SE for O
1
and Sem decided semantics for O
2
.
As it was mentioned in Section 3.1, in the Semantic
Web technologies semantics of a real-world object is
captured within it’s relations to another objects, there-
fore new semantic edge was attached to O
2
. This edge
connects it to the semantic subnetwork, which could
Semantic Spatial Reasoning - Developing a Conceptual Framework for Reasoning with Semantic, Qualitative-Quantitative Spatial
Information
261

O
1
O
2
Figure 6: The network after Sem, Geom application.
be a subject for the QS reasoner on the next iterations,
because O
2
has known SE.
On the next step new objects O
3
, O
4
with known
SE have been introduced by application of TO
3
, TO
4
to the E
3
, E
4
edges respectively (see Figure 7). Here-
with, the E
3
edge has been introduced shortly be-
fore which demonstrates that the translation opera-
tions could be combined with each other in a mean-
ingful ways.
O
3
O
4
E
3
E
4
Figure 7: The network after TO
3
, TO
4
application.
6 CONCLUSIONS
The aim of this work was to investigate reason-
ing with information of mixed types: qualitative-
quantitative spatial and information described with
the help of the Semantic Web technologies to bridge
the gap between geometries and semantics of real-
world objects. As a result we have introduced a con-
ceptual framework called semantic spatial reasoning.
We have developed the translation operations which
are the main part of the framework that enables com-
bined reasoning. Each operation opens a new direc-
tion for further research of it’s software implemen-
tation and practical application in the context of the
combined reasoning. We provided an exemplar idea
for each operation.
The modular structure of the framework is flex-
ible enough to model different practical tasks. For
example, for the task of computing quantitative scene
by it’s text description one might need to implement
the following elements of the framework: qualitative
spatial reasoner, TO
4
and Geom translation opera-
tions. Such an easy decomposition makes the frame-
work useful in different application areas, such as,
GIS, cognitivevision, computer-aided design, data in-
tegration. Since declarative rules are the first class
citizens of the framework, it makes possible to gen-
erate new spatially-enabled knowledge from existing
knowledge, such as, generating implicit consequences
of some spatial events like earthquakes, industrial dis-
asters.
We plan to incorporate all elements of the frame-
work into software application using existed reason-
ers and investigate reasoning capabilities of the result
on real-world tasks in GIS area. We will also investi-
gate how the framework could be generalized to adopt
qualitative temporal reasoning.
ACKNOWLEDGEMENTS
This work was carried out in the framework of the
ALErT project, European Union grant no. 607996.
REFERENCES
Coad, P. and Yourdon, E. (1991). Object-Oriented Design.
Prentice-Hall.
De Felice, G. (2013). Reasoning with mixed qualitative-
quantitative representations of spatial knowledge. Ios
Pr Inc.
Katerinenko, R. and Bessmertnyi, I. (2011). A method
for acceleration of logical inference in the production
knowledge model. Programming and Computer Soft-
ware, 37(4):197–199.
Mackworth, A. K. (1977). Consistency in networks of rela-
tions. Artificial intelligence, 8(1):99–118.
Perry, M. and Herring, J. (2012). Ogc geosparqla geo-
graphic query language for rdf data. version 1.0, ogc
11-052r4, open geospatial consortium.
Schneider, M. (2002). Implementing topological predicates
for complex regions. In Advances in Spatial Data
Handling, pages 313–328. Springer.
Wolter, D. and Wallgr¨un, J. (2012). Qualitative spatial rea-
soning for applications: New challenges and the sparq
toolbox. Qualitative Spatio-Temporal Representation
and Reasoning: Trends and Future Directions, pages
336–362.
KEOD 2015 - 7th International Conference on Knowledge Engineering and Ontology Development
262
