Design of an Autonomous Intelligent Demand-Side Management System
by using Electric Vehicles as Mobile Energy Storage Units by Means of
Evolutionary Algorithms
Edgar Galv´an-L´opez
1
, Marc Schoenauer
2
and Constantinos Patsakis
3
1
School of Computer Science and Statistics, Trinity College Dublin, Dublin, Ireland
2
TAO Project, INRIA Saclay & LRI - Univ. Paris-Sud and CNRS, Orsay, France
3
Department of Informatics, University of Piraeus, Piraeus, Greece
Keywords:
Demand-Side Management, Electric Vehicles, Evolutionary Algorithms, Differential Evolution.
Abstract:
Evolutionary Algorithms (EAs), or Evolutionary Computation, are powerful algorithms that have been used in
a range of challenging real-world problems. In this paper, we are interested in their applicability on a dynamic
and complex problem borrowed from Demand-Side Management (DSM) systems, which is a highly popular
research area within smart grids. DSM systems aim to help both end-use consumer and utility companies
to reduce, for instance, peak loads by means of programs normally implemented by utility companies. In
this work, we propose a novel mechanism to design an autonomous intelligent DSM by using (EV) electric
vehicles’ batteries as mobile energy storage units to partially fulfill the energy demand of dozens of household
units. This mechanism uses EAs to automatically search for optimal plans, representing the energy drawn from
the EVs’ batteries. To test our approach, we used a dynamic scenario where we simulated the consumption of
40 and 80 household units over a period of 30 working days. The results obtained by our proposed approach
are highly encouraging: it is able to use the maximum allowed energy that can be taken from each EV for each
of the simulated days. Additionally, it uses the most amount of energy whenever it is needed the most (i.e.,
high-peak periods) resulting into reduction of peak loads.
1 INTRODUCTION
Evolutionary Algorithms (EAs) (B¨ack et al., 1999;
Eiben and Smith, 2003), also known as Evolution-
ary Computation systems, are influenced by the the-
ory of evolution by natural selection. These algo-
rithms have been with us for some decades and are
very popular due to robust theoretical work developed
around them that have helped us to understand why
they work (e.g, representations’ properties (Galv´an-
L´opez et al., 2010a; Fagan et al., 2010; Galv´an-L´opez
et al., 2008; McDermott et al., 2010)) and to due to
their successful application in a variety of different
problems, ranging from the automated design of an
antenna carried out by NASA (Lohn et al., 2005), the
automated optimisation of game controllers (Galv´an-
L´opez et al., 2010b), the automated evolution of Java
code (Cody-Kenny et al., 2015), to automated design
of combinational logic circuits (Galv´an-L´opez et al.,
2004; Galv´an-L´opez, 2008). EAs can be considered
a “black-box”, as they do not require any specific
knowledge of the fitness function. They work even
when, for example, it is not possible to define a gradi-
ent on the fitness function or to decompose the fitness
function into a sum of per-variable objective func-
tions.
In this work, we are interested in investigating the
applicability of EAs in a dynamic and challenging
problem in Demand-Side Management (DSM) Sys-
tems taken from Smart Grids where, in summary, the
goal is to automatically create fine-grained solutions
that indicate the amount of energy that can be taken
from electric vehicles’ (EVs) batteries to partially sat-
isfy energy demand in residential areas and reducing
electricity peaks, whenever possible. The proposed
approach and fitness functions used in our work (de-
scribed in Section 2) is not amenable to analytic so-
lution or simple gradient-based optimisation, hence
search algorithms such as EAs are required.
DSM is normally considered as a mechanism
or program, implemented by utility companies, to
control the energy consumption at the customer
side (Masters, 2004). DSM is an important research
106
Galván-Lopez, E., Schoenauer, M. and Patsakis, C..
Design of an Autonomous Intelligent Demand-Side Management System by using Electric Vehicles as Mobile Energy Storage Units by Means of Evolutionary Algorithms.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 106-115
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

area in the Smart Grid (SG) community as shown by
the increasing number of publications over the years
(e.g., more than 2,000 papers have been published in
this area where more than two thirds have been pub-
lished since 2010 (Galv´an-L´opez et al., 2014)). A vi-
sual representation of the research conducted in DSM
over the last years can be found in (Galv´an-L´opez
et al., 2015).
DSM programs include different approaches (e.g.,
manual conservation and energy efficiency pro-
grams (pen, 2007), Residential Load Management
(RLM) (Galvan et al., 2012; Mohsenian-Rad et al.,
2010)), where RLM programs based on smart pric-
ing are amongst the most popular methods. The idea
behind smart pricing is to encourage users to manage
their loads, so that they can reduce electricity prices
while, at the same time, the utility companies achieve
a reduction in the peak-to-average ratio (PAR)
1
in
load demand by shifting consumption whenever pos-
sible (Galvan et al., 2012; Galv´an-L´opez et al., 2014).
One of the major limitations of smart pricing is
the fact that the electricity price is proportional to
the electricity demand (i.e., a high number of appli-
ances/devices connected to the grid results in hav-
ing high electricity costs). To alleviate this problem,
we propose the development of a demand-side au-
tonomous intelligent management system that exploit
electric vehicles’ (EV) batteries. More precisely, our
system uses the EV’s batteries to partially and tem-
porarily fulfill the demand of end-use consumers in-
stead of using only the electricity available from a
substation transformer. This is possible thanks to the
vehicle to grid (V2G) technology, which is described
as a system in which electric-drive vehicles can feed
power to the grid with the appropriate communica-
tion/connection technologies acting as mobile gener-
ators of limited output (Kempton and Letendre, 1997;
Kempton and Tomic, 2005).
The deployment of such a system implies several
significant challenges, e.g. different driving patterns
resulting in the amount of energy needed at the time
of departure, amount of energy taken from the EVs’
batteries. To tackle this problem, we use an optimisa-
tion EA.
Thus, the main contribution of this research is
a novel approach to balance the load demand from
dozens of household units using both a substation
transformer and EVs’ batteries as mobile energy stor-
age units
2
by considering the automatic generation of
1
Peak-to-average ratio is calculated by the maximum
load demand for a period of time over the average load
demand, so a lower PAR is normally preferred due to e.g.
maintenance costs (Mohsenian-Rad et al., 2010).
2
In this work, we use the terms “substation trans-
solutions via the use of EAs. To this end, we are in-
terested in maximising, in general, the use of avail-
able energy from the EVs’ batteries while ensuring
that each of the EVs can complete a journey to work,
where the EVs can be charged, and in particular, help-
ing in the reduction of peak loads at the transformer
level by using the most quantity of energy from the
EVs’ batteries. This problem would be simple enough
if it was not for the dynamicity associated to the prob-
lem and if we would not care about keeping the PAR
relatively low.
To achieve this, we allow the DSM system to
make fine-grained decisions (i.e., variable amount of
energy requested) by using a continuous representa-
tion instead of using a discrete representation (i.e.,
turning a device/appliance on or off resulting in feed-
ing/getting a constant amount of energy) as normally
adopted in DSM (Brooks et al., 2010).
To this end, we use a form of EAs, called Dif-
ferential Evolution (DE) (Storn and Price, 1997), that
allows us to achieve this. More specifically, DE uses
a vector of real-valued functions and we use them to
represent an individual (potential solution) that speci-
fies an energy consumption scheduling vector, which
in turn indicates the amount of energy that should be
taken from the EVs’ batteries aiming at fulfilling the
goals previously described (e.g., maximising the en-
ergy consumption availablefrom the batteries while at
the same time reducing peak loads at the transformer
level with associated constraints such as guaranteeing
that each EV would complete a journey to work). De-
tails on how this algorithm works and its adoption in
this research are described in Section 2.
The rest of this paper is organised as follows. In
the following section we introduce DE and present
our proposed approach. In Section 3, we present the
experimental setup used in this work and Section 4
discusses the findings of our approach. Finally, in
Section 5 we draw some conclusions.
2 PROPOSED APPROACH
2.1 Background
There are multiple EAs methods, such as Genetic
Algorithms (GAs) (Goldberg, 1989), Genetic Pro-
gramming (GP) (Koza, 1992), Differential Evolution
(DE) (Storn and Price, 1997). All these methods use
evolution as an inspiration to automatically generate
potential solutions for a given problem. They differ,
former” and “EV’s batteries” to differentiate between the
two sources of energy.
Design of an Autonomous Intelligent Demand-Side Management System by using Electric Vehicles as Mobile Energy Storage Units by
Means of Evolutionary Algorithms
107
mainly, in the representation used (i.e., encoding of
a solution). For example, the typical representation
used in GAs is fixed bitstrings, GP’s typical repre-
sentation is tree-like structures, DE uses a vector of
real-valued functions.
In this work, we use a DE algorithm given its nat-
ural representation (i.e., real-valued functions). Other
bio-inspired algorithms can also use this type of rep-
resentation, however, in this work we decided to use a
DE given its efficiency for global optimisation over
continuous search spaces (Storn and Price, 1997).
By using this type of representation, we can have
a more fine-grained action granularity (e.g., in this
work, each element in the vector represents how much
energy will be taken from the EVs’ batteries to feed
household units), instead of using a more limited
representation such as a bitstring representation that
could indicate to take a pre-defined amount of energy
(i.e., on or off) from EVs’ batteries to partially fulfill
energy consumption from household units. We fur-
ther discuss this later in this section.
The goal of DE is to evolve NP D-dimensional
parameter vectors x
i,G
= 1, 2, ··· , NP, so-called pop-
ulation, which encode the potential solutions (indi-
viduals), i.e., x
i,G
= {x
1
i,G
··· , x
D
i,G
}, i = 1, · ·· , NP to-
wards the global optimum solution (e.g., highest val-
ues when maximising a cost function). The initial
population is randomly generated and this should be
done by spreading the points across the entire search
space (e.g., this could be achievedby distributingeach
parameter on an individual vector with uniform dis-
tribution between lower and upper bounds x
l
j
and x
u
j
).
To automatically evolve these potential solutions over
generations via the definition of a fitness function, DE
uses the most common bio-inspired operators as com-
monly carried out in EAs: mutation and crossover to
find the global optimum solution. Each of these oper-
ators is briefly explained in the following lines (refer
to (Qin et al., 2009; Storn and Price, 1997) for a de-
tailed description on how they work).
The mutation operator generates a mutant vector
following one of the following strategies:
DE/rand/1
v
i,G
= x
r
i
1
,G
+ F ·(x
r
i
2
,G
− x
r
i
3
,G
)
DE/best/1
v
i,G
= x
best,G
+ F ·(x
r
i
1
,G
− x
r
i
2
,G
)
DE/rand-to-best/1
v
i,G
= x
i,G
+ F ·(x
best,G
− x
i,G
) + F · (x
r
i
1
,G
− x
i
2
,G
)
DE/best/2
v
i,G
= x
best,G
+ F ·(x
r
i
1
,G
− x
r
i
2
,G
) + F · (x
r
i
3
,G
− x
r
i
4
,G
)
DE/rand/2
v
i,G
= x
r
i
1
,G
+ F ·(x
r
i
2
,G
− x
r
i
3
,G
) + F · (x
r
i
4
,G
− x
r
i
5
,G
)
where indexes r
1
, r
2
, r
3
, r
4
∈ {1, 2, ··· , NP} are ran-
dom and mutually different. F is a real and con-
stant factor ∈ [0, 2] for scaling differential vectors and
x
best,G
is the individual with best fitness value (e.g.,
highest value for a maximisation function) in the pop-
ulation at generation G.
The crossover operator increases the diversity of
the mutated parameter vectors and is defined by:
v
i,G+1
= (v
1i,G+1
, v
2i,G+1
, ··· , v
Di,G+1
)
where:
v
ji,G+1
=
v
ji,G+1
if randb( j) ≤ CR or j = rnbr(i),
x
ji,G
otherwise
where j = 1, ·· · , D, randb( j) is the j
th
evaluation of
a uniform random number generator with outcome
∈ [0, 1]. CR is the constant crossover rate ∈ [0, 1].
rnbr(i) is a randomly chosen index ∈ 1, 2, · ·· , D
which ensures that u
i,G+1
receives at least one param-
eter value from u
i,G+1
.
The performance of the DE algorithm depends on
different factors, such as the values associated to the
parameters (e.g., population size) as well as the vari-
ant of the operator used (e.g., variant of the muta-
tion operator). This, intuitively means, that some pre-
liminary runs would be normally required to deter-
mine which variant of an operator performs better on
a given problem. We further discuss this in the fol-
lowing section.
2.2 Proposed Representation and
Fitness Function
We nowextend the natural DE representationto tackle
the problem described throughout the paper and pro-
ceed to define the fitness function (cost function) that
allows the algorithm to automatically guide the evo-
lutionary search.
Let N denote the number of household units
(users), where the number of household units is N ,|
N |. For each household n ∈ N, let l
t
n
denote the total
load at time t ∈ T , {t
i
, ··· , t
f
}. Without loss of gen-
erality, we assume that time granularity is 15 minutes.
The load for household n, from t
i
to t
f
, is denoted by:
l
n
, [l
t
i
n
, ··· , l
t
f
n
] (1)
From this, we can calculate the load across all
household units N at each time t ∈ [t
i
,t
f
] as follows:
L
t
,
∑
n∈N
l
t
n
(2)
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
108

Similarly, let M denote the number of electric ve-
hicles available in N. For each electric vehicle m ∈ M,
let E
t
m
denote the energy that can be taken from the
EV at time t ∈ T , {t
i
, ··· , t
f
}. Without loss of gen-
erality, we assume that time granularity is again 15
minutes. The total energy taken from an EV from t
i
until t
f
is denoted by:
E
m
, [E
t
i
m
, ··· , E
t
f
m
] (3)
We use this as a foundation to represent an indi-
vidual that specifies an energy consumption schedul-
ing vector. More specifically, an individual is repre-
sented by:
E
M
,
E
t
i
m
1
, ··· , E
t
f
m
1
E
t
i
m
2
, ··· , E
t
f
m
2
.
.
.
E
t
i
m
M
, ··· , E
t
f
m
M
(4)
where each E
t
m
is a real value representing the amount
of energy taken from an EV’s battery. Each row rep-
resents the behaviour of a single EV over the full pe-
riod; each column represents the behaviour of all EVs
at a single time-slot. An individual in the EA is just
a matrix E
M
, unrolled to give a vector of real-valued
functions, that is:
E
t
i
1
, ··· , E
t
f
1
, E
t
i
2
, ··· , E
t
f
2
, ··· , E
t
i
M
, ··· , E
t
f
M
(5)
Based on these definitions, the total energy taken
across all M EVs at each t ∈ [t
i
,t
f
] can be calculated
as:
E
t
,
∑
m∈M
E
t
m
(6)
To automatically find good energy consumption
scheduling solutions, defined in Equation 4, we need
to define a fitness function (cost function) that indi-
cates the quality of our evolved solution. First, we
focus our attention in designing a cost function that
tries to create valid solutions in terms of using the
maximum allowed energy from each EV (i.e., guar-
anteeing that a minimum state of charge (SoC) is left
at the time of departure t
f
).
From Equation 3, we know the amount of energy
available from m ∈ M at any given period of time t
denoted by E
t
m
. Because each EV can be charged at
work and the distance from home to work remains
constant, it is fair to assume the knowledge of a
minimum SoC expressed in kW, denoted as m
SoC
, at
the time of departure t
f
for each m ∈ M, so that it can
reach work and be recharged at a lower rate. From
this, we let the DE to assess a potential solution,
denoted in Equation 4, measuring the amount of
energy taken from the EVs.
This is defined as:
f
l
(E
M
) , maximise
1
#{m ∈ M}
∑
m∈M
E
m
+ (E
m
+ 1)(m
SoC
− E
t
i
m
)
m
SoC
E
t
i
m
− m
SoC
(7)
Equation 7 guides evolutionary search towards a
local optimum solution since it only encourages the
finding of solutions that maximise the use of allow-
able energy taken from EVs’ batteries. Thus, there is
a necessity to further enrich this equation, so that a
higher quantity of energy is taken from the EVs’ bat-
teries whenever deemed necessary (e.g., higher con-
sumption during high peak periods). We achieve this
by using Equations 2 and 6 that indicate the load
across all household units L
t
at time t and the total
energy taken across all EVs E
t
at time t, respectively;
and we define a degree of importance for each time
slot as t
r
. Putting everything together we have:
f
g
(E
M
) , f
l
(E
M
) + maximise
1
#{m ∈ M}
t
r
t
f
∑
t=t
i
E
t
L
t
t
r
∀t
r
< T
r
−
1
#{m ∈ M}
t
r
t
f
∑
t=t
i
E
t
L
t
t
r
∀r ≥ T
r
(8)
where T
r
is a threshold that denotes the number of
time slots that are considered critical (i.e., high peak
period). In this work, as defined in this section and
we discuss further afterwards, a number of time slots
is defined by t
i
and t
f
, where a third is considered
critical (T
r
= 20).
3 EXPERIMENTAL SETUP
3.1 Household Units
To test the scalability of our proposed approach, we
simulated the consumption of 40 and 80 household
units, where each of them uses between 10 and 20
appliances. As indicated throughout the paper, the
goal is to use EVs’ batteries in an intelligent way to
partially satisfy energy demand from the end-use con-
sumers (recall that we work under the assumption that
the EVs can be charged at work).
To this end, we simulated that around 20% of
household units account for an EV. To makethis prob-
lem dynamic, we allowed the patterns of arrival (t
i
),
departure (t
f
) and initial State of Charge (SoC) for
each of the EVs to vary for each of the 30 simulated
working days. More specifically, the arrival and de-
parture time for each of the EVs have a 90-minute
Design of an Autonomous Intelligent Demand-Side Management System by using Electric Vehicles as Mobile Energy Storage Units by
Means of Evolutionary Algorithms
109

time frame starting at t
i
=17:00 and t
f
=6:30, respec-
tively (i.e., arrival time could be between 17:00 and
18:30, whereas departure time could be between 6:30
and 8:00). The initial SoC
t
i
for each of the EVs for
each of the simulated days is set between 48% and
60% and the final SoC
t
f
is set between 30% and 35%
to allow each EV to reach work. Table 1 summarises
the parameters used to simulate our scenario. We ran
our simulations for a period of 30 days of simulated
time.
3.2 Scenarios
As indicated in Section 2, we defined a bottom-up
approach, where we defined, first, a fitness function
that tries to maximise the energy that can be taken
from the EVs’ batteries while ensuring that each of
them reaches work, described in Equation 7, and then
we enriched the fitness function by trying to also re-
duce the highest load demands at the substation trans-
former, described in Equation 8 (i.e., use the most
amount of energy from the batteries at high-peak time
while at the same time ensuring the PAR remains
low). We tested both fitness functions for 40 and 80
household units, resulting in four different scenarios.
3.3 Differential Evolution
As mentioned in Section 2, differential evolution’s
performance, as any other evolution-based algorithm,
depends, among other things, on the values associ-
ated to the parameters that need to be specified for
the algorithm (e.g., population size, number of gener-
ations), in general, and in the type of operator used, in
particular.
No a priori knowledge is available to presume
which mutation operator will perform better in the
previously defined problem. To this end, we exe-
cuted 30 independent runs of our proposed approach
for each of the mutation variants, e.g., DE/rand/1,
DE/best/1, (150
3
independentruns in total to find only
the best mutation strategy) using the first proposed fit-
ness function (Equation 7) which maximises the en-
ergy taken from 11 EVs’ batteries to complement the
energy consumption of 40 household units averaged
over 30 days. Figure 1 shows the performance by
measuring the average of best fitness per generation
for each of the five mutation variants, using a popula-
tion size of 500 individuals and 200 generations.
Clearly, the mutation strategy DE/rand/2 achieved
the best performance and we used it to run our exper-
iments to automatically find a (nearly) optimal solu-
3
30 independent runs * 5 variants of the mutation oper-
ator.
20 40 60 80 100 120 140 160 180 200
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Number of generations
Average of best fitness
DE/best/1
DE/best/2
DE/rand/1
DE/rand/2
DE/rand−to−best/1
Figure 1: Average of best fitness values of 30 independent
runs for each of the five types of mutation operators tested
in this work, using 500 individuals and 200 generations, to
maximise energy consumption from electric vehicles’ bat-
teries (Equation 7). Higher values are preferred.
tion. To obtain meaningful results, we performed 30
independent runs for each of the scenarios explained
in the previous paragraphs (we executed 30 * 4 runs in
total
4
). Runs were stopped when the maximum num-
ber of generations was reached.
As mentioned in Section 2, every element of the
DE vector represents how much energy can be taken
from the batteries of the EVs. We make a decision ev-
ery 15 minutes. Thus, the length of the individual that
represent the solution is the number of time slots de-
fined between 17:00 and 8:00am, whereas the height
is defined by the number of electric vehicles used, as
defined in Equation 4. The parameters used in our
experiments are summarised in Table 2.
4 RESULTS
In the following paragraphs, we will analyse: (a) how
the EVs’ batteries were used to partially satisfy the
demand of a set of household units, (b) when the high-
est consumption from EVs’ batteries occurred, and
finally, (c) the implications of the new consumption
model via the analysis of the peak-to-average-ratio.
4.1 Maximising Energy Consumption
from EVs’ batteries
Let us start analysing our approach on how the
4
30 independent runs, 4 different scenarios (i.e., 40 and
80 household units, trying to maximise: (a) energy con-
sumption from EVs, and (b) energy consumption from EVs
considering reducing highest load peaks; for each of the set
of household units used in this work).
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
110
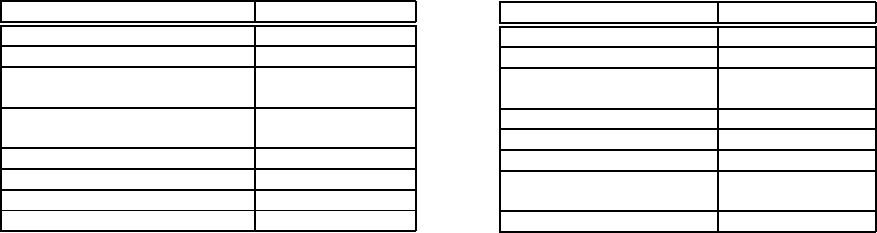
Table 1: Summary of parameters used for our smart grid
system.
Parameter Value
Number of household units 40, 80
Number of appliances Uniform in [10,20]
Number of EVs ≈ 20% of houses
have one EV
Arrival and departure time t
i
=[17:00,18:30]
t
f
=[6:30,8:00]
Frequency of making a decision 15 minutes
Number of times slots T 60
State of Charge at t
i
Uniform in [48, 60]
State of Charge at t
f
Uniform in [30, 35]
Table 2: Summary of parameters used for our evolution-
ary algorithm.
Parameter Value/Comment
Population size 500
Length of the chromosome T (see Table 1)
Height of the chromosome Number of EVs
(see Table 1)
Generations 200
Crossover rate 0.5
Mutation strategy DE/rand/2
Termination criterion Maximum number
of generations
Independent runs 30
batteries of the EVs helped to partially satisfy the con-
sumption demand from a set of household units. The
averaged consumption over a period of 30 days of
these household can be seen in Figure 2 (a, b) and
(c, d) for 40 and 80 houses, respectively.
In the left-hand side of this figure, we show the
distribution of consumption of both transformer and
EVs’ batteries proposed by the differential evolution
algorithm, when trying to maximise the consumption
of energy from the EVs’ batteries via Equation 7.
More specifically, it aims at using all the possible en-
ergy available from the batteries while guaranteeing
that each EV has a minimal SoC at the time of depar-
ture (see Table 1) that guarantees that each EV will
reach work. The white-filled bars represent the en-
ergy taken from the substation transformer whereas
the remaining energy consumption to fulfill the en-
ergy demand is taken from the EVs’ batteries. The
latter is shown by the black-filled bars.
Because we are interested in using the EVs’ bat-
teries as mobile energy storage units, we are partic-
ularly interested in seeing how the energy consump-
tion from these is managed by the differential evo-
lution algorithm. In the first instance of our algo-
rithm (i.e., maximising the energy consumption from
the batteries of EVs with associated constraints, as
mentioned previously), it is expected that the energy
taken from the batteries would not follow a particu-
lar pattern (e.g., there is no correlation between the
amount of energy consumption from EVs and the en-
ergy needed by a number of household units). Indeed,
this is the case as seen in the left-hand side of Fig-
ure 2. For example, notice how the consumption from
EVs’ is proportionally similar during both high-peak
(e.g., 18:30 - 19:30) and low-peak periods (e.g., 22:00
- 23:00).
The situation is more encouraging when we con-
sider the second instance of our algorithm (i.e.,
maximising energy consumption from EVs’ batteries
while considering high-peak periods), shown in the
right-hand side of Figure 2. As it can be observed, the
proposed enriched fitness function, shown in Equa-
tion 8, is able to automatically produce results that
can reduce the load peaks from the substation trans-
former by using more electricity from the EVs’ bat-
teries. For example, notice how the consumption of
energy from batteries is higher during high-peak pe-
riods (e.g., 18:30 - 19:30) and lower during low-peak
periods (e.g., 22:00 - 23:00).
4.2 Consumption from EV’s batteries
In the previous paragraphs, we discussed and showed
the results obtained by our approach using two cost
functions, formally described in Equations 7 and 8.
It is clear that the latter function is able to use a
higher quantity of energy from the EVs’ batteries dur-
ing high-peak periods compared to the effects when
using the former function, as shown in the right-hand
and left-hand side of Figure 2, respectively, using 40
and 80 household units. This averaged result over a
period of 30 simulated working days, however, does
not inform us in detail when the highest consumption
from batteries occurred (e.g., when and how much
consumption from the batteries for every of the simu-
lated days occurred).
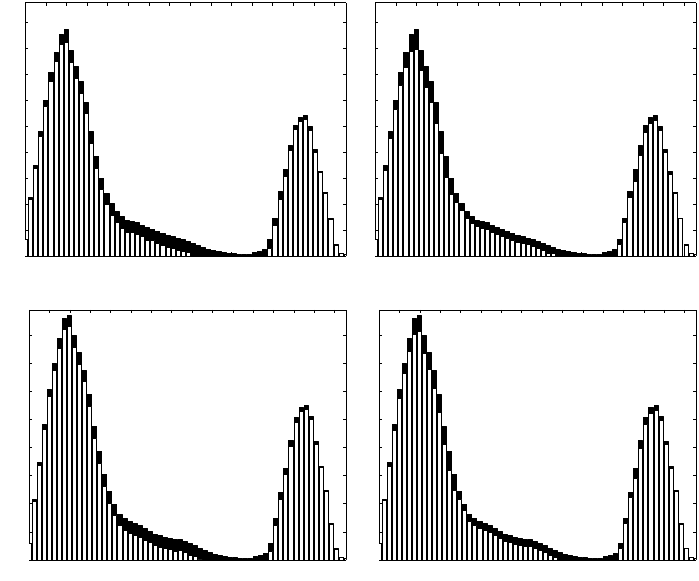
To this end, we kept track of the consumption
from the EVs’ batteries during the simulated period of
time (i.e., 17:00 - 8:00) for every day of the simulated
days. The patterns of such consumption are shown
in Figure 3 (a, b) and (c, d) for 40 and 80 household
units, respectively.
Let us start our analysis when maximising the en-
ergy that can be taken from the batteries while ensur-
ing that each EV has the minimum SoC at the time
of departure, defined in Equation 7. The consump-
tion pattern of this is shown in Figure 3 (a) and (c) for
40 and 80 household units, respectively. It should be
noted that the higher the consumption from batteries
is, the darker the dot. We can see that a random pat-
tern is achieved by the cost function shown in Equa-
tion 7. That is, for every recorded day, shown in the y-
Design of an Autonomous Intelligent Demand-Side Management System by using Electric Vehicles as Mobile Energy Storage Units by
Means of Evolutionary Algorithms
111
17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8
0
10
20
30
40
50
60
70
80
90
Time of day (15 mins. granularity)
Consumption (kWh)
17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8
0
10
20
30
40
50
60
70
80
90
Time of day (15 mins. granularity)
Consumption (kWh)
(a) (b)
17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8
0
20
40
60
80
100
120
140
160
Time of day (15 mins. granularity)
Consumption (kWh)
17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8
0
20
40
60
80
100
120
140
160
Time of day (15 mins. granularity)
Consumption (kWh)
(c) (d)
Figure 2: Average of 30-day energy consumption for 40 (top) and 80 (bottom) household units, each using between 10-20
appliances. The consumption of energy from the transformer alone is shown by the white-filled bars whereas the black-filled
bars represent the consumption taken from electric vehicles’ batteries. Maximising energy consumption from electric vehicles
only and maximising energy consumption from electric vehicles considering reducing highest load peaks are shown in the
left-hand side and right-hand side of the figure, respectively.
axis, the amount of energy taken from the batteries is
rather random regardless of the period time, shown in
the x-axis, except from 17:00-18:30 and 6:30 – 8:00,
where the consumption from batteries is low. This
can be explained due to the availability of EVs during
these periods. That is, as indicated in Section 3, each
EV has its own time of arrival and departure which
varies during these periods of time.
We continue our analysis on the proposed en-
riched maximisation cost function, see Equation 8,
that aims at using the most amount of energy from
the batteries of the EVs while ensuring that each has a
minimum SoC at the time of departure, and that tries
to reduce the highest peak loads. The consumption
pattern from the batteries is shown in Figure 3 (b) and
(d) for 40 and 80 household units, respectively. This
is a mirror image of what we discussed in the previ-
ous paragraph. That is, there is a well-defined pattern
for each of the simulated days, shown in the y-axis,
during the period of study, shown in the x-axis of the
figure. We can observe that this cost function indeed
achievesat using the most amount of energy when it is
needed the most (high-peaks) as shown by the darker-
filled squares while ensuring that the constraints are
not violated (e.g., minimum SoC at the time of depar-
ture).
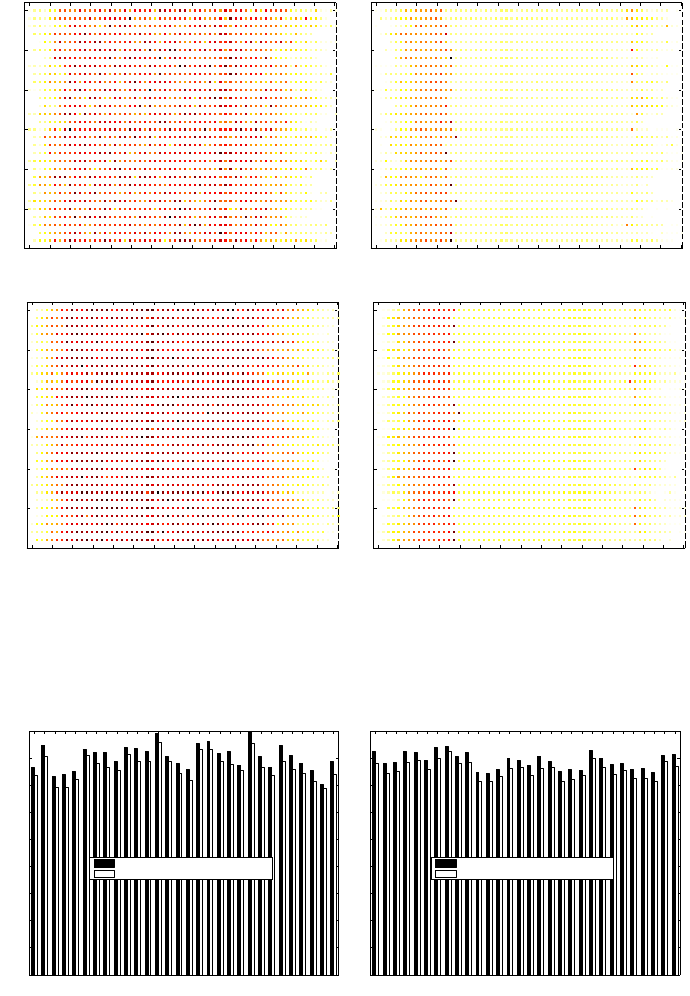
4.3 Peak-To-Average Ratio
As indicated previously, the peak-to-average ratio
(PAR) is calculated by the maximum load demand for
a period of time over the average load demand for the
same period. It has been shown that a lower PAR is
preferred (Mohsenian-Rad et al., 2010).
We calculated the PAR considering the consump-
tion from the substation transformer. Figure 4 shows
the PAR for 40 (left-hand side) and 80 (right-hand
side) household units for each of the 30 working sim-
ulated days using our proposed approach. It is easy to
observe that a higher PAR is achieved by the fitness
(cost) function formally defined in Equation 7, which
goal is to use the most amount of energy from EVs’
batteries while at the same time aims at guaranteeing
that each EV has a minimum SoC at the time of depar-
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
112
17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8
0
5
10
15
20
25
30
Time of day (15 mins. granularity)
Days
17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8
0
5
10
15
20
25
30
Time of day (15 mins. granularity)
Days
(a) (b)
17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8
0
5
10
15
20
25
30
Time of day (15 mins. granularity)
Days
17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8
0
5
10
15
20
25
30
Time of day (15 mins. granularity)
Days
(c) (d)
Figure 3: Energy quantity taken from 11 (a, b) and 21 (c, d) electric vehicles over the range of time period studied in this
work, from 17:00 until 8:00 (shown in the x-axis), for 30 days (shown in the y-axis) to help with the energy consumption of
40 (a, b) and 80 (c, d) household units. Darker-filled circles represent higher energy quantity taken from the EVs’ batteries.
The enriched cost function, described in Equation 8, follows a well-defined desired pattern (b, d), whereas the cost function
that tends to find local optimum solutions, described in Equation 7, tends to have a rather undesirable random pattern (a, c).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Day
Peak−to−average ratio
Optimising consumption of energy battery
Optimising reduction of highest electricity peaks
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Day
Peak−to−average ratio
Optimising consumption of energy battery
Optimising reduction of highest electricity peaks
Figure 4: Peak-to-average ratio (PAR) load demand achieved by our proposed approach when trying to maximise energy
consumption from EVs’ batteries (black-filled bars) vs. when trying to maximise energy consumption from EVs’ batteries
while aiming at reducing highest load peaks (white-filled bars), for 40 and 80 household units shown at the left-hand side and
right-hand side of the figure, respectively. A lower PAR is preferred.
ture compared to that PAR achieved by the enriched
fitness function formally described in Equation 8 that
is built on the top of Equation 7, which also tries to
reduce the highest peak loads.
This, in fact, is to be expected given that the fitness
function described in Equation 8 does consider an as-
sociated ranking system (recall that a third of time
slots are considered critical, i.e., high peak period)
that is able to reflect smoothly the consumption from
the substation transformer as shown by the low PAR
achievedby this enriched fitness function for each day
of the 30 simulated days, denoted by the white-filled
Design of an Autonomous Intelligent Demand-Side Management System by using Electric Vehicles as Mobile Energy Storage Units by
Means of Evolutionary Algorithms
113
bars in Figure 4.
5 CONCLUSIONS
Evolutionary Algorithms are very popular given its
applicability in a range of static problems. In this
work, we focus our attention on using a differen-
tial evolution (DE) algorithm in a fairly complex and
dynamic problem taken from Demand-Side Manage-
ment (DSM) systems. DSM systems play an impor-
tant role in the SG. Their importance can be under-
stood by considering the new challenges that are con-
tinuously introduced to the grid, for example, electric
appliances that could double the average household
(e.g., electric vehicles). The correct design of a DSM
manages to use the available energy efficiently, with-
out the necessity of installing new electricity infras-
tructure.
In the specialised literature, there are several tech-
niques adopted by DSM programs. Perhaps, the most
popular techniques are those inspired on smart pric-
ing. Briefly, the idea is to incentivise end-consumers
to shift energy consumption to hours when the elec-
tricity price is low, reducing both electricity costs and
energy-load consumption.
We believe that another important research area
worth exploring in DSM is to exploit “new” avail-
able technologies. In particular, we regard that there
is a lot of potential in utilising EVs’ batteries as mo-
bile energy storage units. To this end, we propose
a demand-side autonomous intelligent management
system that uses them to partially fulfill the demand of
end-use consumers instead of using only the electric-
ity available from a substation transformer, whenever
possible. To this end, we use a DE algorithm, that
is able to automatically create fine-grained solutions
that indicate the amount of energy that can be taken
from the EVs, rather than adopting a more constraint
representation (e.g., on/off of EVs).
The results achieved by our proposed approach
are highly encouraging. That is, we showed how DE
is able to correctly use the maximum amount of en-
ergy while ensuring a minimum SoC for each EV for
each day of the 30 simulated working days. We built
upon this to automatically find the best possible con-
figuration of values (i.e., consumption from batteries)
whenever it was needed the most (i.e., high-peaks),
while simultaneously, demonstrating that it was pos-
sible to do so by keeping the PAR low.
ACKNOWLEDGEMENTS
Edgar Galv´an L´opez’s research is funded by an ELE-
VATE Fellowship, the Irish Research Council’s Ca-
reer Development Fellowship co-funded by Marie
Curie Actions. The first author would also like to
thank the TAO group at INRIA Saclay & LRI - Univ.
Paris-Sud and CNRS, Orsay, France for hosting him
during the outgoing phase of the ELEVATE Fellow-
ship. The authors would like to thank all the review-
ers for their useful comments that helped us to signif-
icantly improve our work.
REFERENCES
(2007). Pacific Northwest GridWise Testbed Demonstration
Projects, Part I. Olympic Peninsula Project.
B¨ack, T., Fogel, D. B., and Michalewicz, Z., editors (1999).
Evolutionary Computation 1: Basic Algorithms and
Operators. IOP Publishing Ltd., Bristol, UK.
Brooks, A., Lu, E., Reicher, D., Spirakis, C., and Weihl, B.
(2010). Demand dispatch: Using real-time control of
demand to help balance generation and load. IEEE
Power & Energy Magazine,, 8:20 – 29.
Cody-Kenny, B., Galv´an-L´opez, E., and Barrett, S. (2015).
locogp: Improving performance by genetic program-
ming java source code. In Proceedings of the Com-
panion Publication of the 2015 on Genetic and Evolu-
tionary Computation Conference, GECCO Compan-
ion ’15, pages 811–818, New York, NY, USA. ACM.
Eiben, A. E. and Smith, J. E. (2003). Introduction to Evolu-
tionary Computing. Springer Verlag.
Fagan, D., ONeill, M., Galv´an-L´opez, E., Brabazon,
A., and McGarraghy, S. (2010). An analysis of
genotype-phenotype maps in grammatical evolution.
In Esparcia-Alczar, A., Ekrt, A., Silva, S., Dignum, S.,
and Uyar, A., editors, Genetic Programming, volume
6021 of Lecture Notes in Computer Science, pages
62–73. Springer Berlin Heidelberg.
Galvan, E., Harris, C., Dusparic, I., Clarke, S., and Cahill,
V. (2012). Reducing electricity costs in a dynamic
pricing environment. In Proc. Third IEEE Interna-
tional Conference on Smart Grid Communications
(SmartGridComm), pages 169 – 174, Tainan, Taiwan.
IEEE Press.
Galv´an-L´opez, E. (2008). Efficient graph-based genetic
programming representation with multiple outputs.
International Journal of Automation and Computing,
5(1):81–89.
Galv´an-L´opez, E., Curran, T., McDermott, J., and Car-
roll, P. (2015). Design of an autonomous intelligent
demand-side management system using stochastic op-
timisation evolutionary algorithms. Neurocomputing,
170:270–285.
Galv´an-L´opez, E., Dignum, S., and Poli, R. (2008).
The effects of constant neutrality on performance
and problem hardness in gp. In Proceedings of
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
114
the 11th European conference on Genetic program-
ming, EuroGP’08, pages 312–324, Berlin, Heidel-
berg. Springer-Verlag.
Galv´an-L´opez, E., Harris, C., Trujillo, L., V´azquez, K. R.,
Clarke, S., and Cahill, V. (2014). Autonomous
demand-side management system based on monte
carlo tree search. In IEEE International Energy Con-
ference (EnergyCon), pages 1325 – 1332, Dubrovnik,
Croatia. IEEE Press.
Galv´an-L´opez, E., McDermott, J., O’Neill, M., and
Brabazon, A. (2010a). Defining locality in ge-
netic programming to predict performance. In IEEE
Congress on Evolutionary Computation, pages 1–8.
IEEE.
Galv´an-L´opez, E., Poli, R., and Coello, C. (2004). Reusing
code in genetic programming. In Keijzer, M., OR-
eilly, U.-M., Lucas, S., Costa, E., and Soule, T., edi-
tors, Genetic Programming, volume 3003 of Lecture
Notes in Computer Science, pages 359–368. Springer
Berlin Heidelberg.
Galv´an-L´opez, E., Swafford, J. M., O’Neill, M., and
Brabazon, A. (2010b). Evolving a ms. pacman con-
troller using grammatical evolution. In Chio, C. D.,
Cagnoni, S., Cotta, C., Ebner, M., Ek´art, A., Esparcia-
Alc´azar, A., Goh, C. K., Guerv´os, J. J. M., Neri, F.,
Preuss, M., Togelius, J., and Yannakakis, G. N., ed-
itors, EvoApplications (1), volume 6024 of Lecture
Notes in Computer Science, pages 161–170. Springer.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-
timization and Machine Learning. Addison-Wesley
Longman Publishing Co., Inc., Boston, MA, USA, 1st
edition.
Kempton, W. and Letendre, S. E. (1997). Electric vehicles
as a new power source for electric utilities. Trans-
portation Research Part D: Transport and Environ-
ment, 2(3):157 – 175.
Kempton, W. and Tomic, J. (2005). Vehicle-to-grid power
fundamentals: Calculating capacity and net revenue.
Journal of Power Sources, 144(1):268–279.
Koza, J. R. (1992). Genetic Programming: On the Pro-
gramming of Computers by Means of Natural Selec-
tion. MIT Press, Cambridge, MA, USA.
Lohn, J., Hornby, G., and Linden, D. (2005). An evolved
antenna for deployment on nasas space technology 5
mission. In OReilly, U.-M., Yu, T., Riolo, R., and
Worzel, B., editors, Genetic Programming Theory and
Practice II, volume 8 of Genetic Programming, pages
301–315. Springer US.
Masters, G. M. (2004). Renewable and Efficient Electric
Power Systems. Wiley-Interscience.
McDermott, J., Galv´an-L´opez, E., and ONeill, M. (2010). A
fine-grained view of gp locality with binary decision
diagrams as ant phenotypes. In Schaefer, R., Cotta, C.,
Koodziej, J., and Rudolph, G., editors, Parallel Prob-
lem Solving from Nature, PPSN XI, volume 6238 of
Lecture Notes in Computer Science, pages 164–173.
Springer Berlin Heidelberg.
Mohsenian-Rad, A., Wong, V., Jatskevich, J., Schober, R.,
and Leon-Garcia, A. (2010). Autonomous demand-
side management based on game-theoretic energy
consumption scheduling for the future smart grid.
Smart Grid, IEEE Transactions on, 1(3):320 –331.
Qin, A. K., Huang, V. L., and Suganthan, P. N. (2009). Dif-
ferential evolution algorithm with strategy adaptation
for global numerical optimization. Trans. Evol. Comp,
13(2):398–417.
Storn, R. and Price, K. (1997). Differential evolution a sim-
ple and efficient heuristic for global optimization over
continuous spaces. Journal of Global Optimization,
11(4):341–359.
Design of an Autonomous Intelligent Demand-Side Management System by using Electric Vehicles as Mobile Energy Storage Units by
Means of Evolutionary Algorithms
115
