Investigation of the Minimum Conditions for Reliable Estimation of

Clinically Relevant HRV Measures

Introducing a Novel Approach to the Validation of HRV Measurement Systems

Esben Ahrens

, Helge B. D. Sorensen

, Henning Langberg

, Karsten Hoppe

and Dorthe Bodholt Saadi

Department of Electrical Engineering, Technical University of Denmark,

Ørsteds Plads Building 348, 2800 Kgs. Lyngby, Denmark

Department of Public Health, Copenhagen University, Henrik Pontoppidansvej 4, 1014 Copenhagen K, Denmark

DELTA Danish Electronics, Lights & Acoustics, Venlighedsvej 4, 2970 Hørshom, Denmark

Keywords:

Heart Rate Variability, Jitter, Ectopic Beat.

Abstract:

The R-peak localization error (jitter) of a heart rate variability (HRV) system has a great impact on the values

of the HRV measures. Only a few studies have analyzed this subject and purely done so from the aspect of

choice of sampling frequency. In this study we provide an overview of the various factors that comprise the

jitter of a system. We propose a method inspired by the ﬁeld of signal averaged electrocardiography (SAECG)

that allows for a quantiﬁcation of the jitter of any HRV system that records and stores the raw ECG signal.

Furthermore, with this method the differences between the HRV measures of the system and HRV measures

corresponding to the physiological truth can be quantiﬁed. The method is used to obtain the physiologically

true R-peak locations of subjects from Physionet’s ‘Normal Sinus Rhythm Database’. The effects of jitter are

then analyzed via mathematical modelling for short-term and long-term HRV for various HRV measures. The

effects of abnormal beats and missed and false detections are analyzed as well.

1 INTRODUCTION

Evaluation of heart rate variability (HRV) has been

acknowledged to provide a reliable reﬂection of the

autonomic modulation of the normal heart rhythm.

Different HRV measures have thus been suggested to

contain clinically relevant information about diseases

related to autonomic dysfunction, e.g. assessment of

diabetic neuropathy (AHA and ESC, 1996). One of

the major HRV research areas is related to risk strat-

iﬁcation in populations with myocardial infarction,

congestive heart failure, or left ventricular dysfunction.

A brief review of the most relevant studies related to

this risk stratiﬁcation is provided in (Huikuri and Stein,

2013). They generally ﬁnd that based on the available

data, abnormal HRV measures are a general risk factor

for cardiac death in patients after myocardial infarction

(Huikuri and Stein, 2013). However, they also note

that most observational studies achieve low sensitivity

and low negative predictivity for adverse outcomes

using HRV measures (Huikuri and Stein, 2013). This

suggests that more research and methodological deve-

lopment is needed in this area. As a part of a continued

research effort, we therefore consider it highly relevant

to take a closer look at the prerequisites for obtaining

reliable HRV measures. This reliability is primarily

limited by the ability to obtain uninterrupted and ac-

curate series of normal RR intervals (Citi et al., 2012).

Furthermore, the emergence of HRV analysis in vari-

ous health management applications makes it highly

relevant to obtain greater knowledge about the mini-

mum conditions needed to obtain reliable estimates of

HRV measures.

Causal Analysis of NN Series Errors.

The quality

of the obtained NN (normal-to-normal) series might

be reduced by several different sources of error. Fig-

ure 1 gives an overview of these sources. One of the

main contributors to errors in the NN series is the inter-

ruptions caused by QRS detection errors or abnormal

beats.

The other main contributor to errors in the NN

series is jitter (localization error) in the automatic de-

tection of the exact R-peak location. This jitter might

be caused by imprecise digitization of the true phy-

Ahrens, E., Sorensen, H., Langberg, H., Hoppe, K. and Saadi, D..

Investigation of the Minimum Conditions for Reliable Estimation of Clinically Relevant HRV Measures - Introducing a Novel Approach to the Validation of HRV Measurement Systems.

In Proceedings of the 3rd International Congress on Cardiovascular Technologies (CARDIOTECHNIX 2015), pages 30-38

ISBN: 978-989-758-160-1

Causal Analysis of NN Series Errors































Figure 1: Overview of the most important potential causes

of errors in the NN series. The presence of each of these

errors might inﬂuence the reliability of the estimated HRV

measures. Low QRS detection performance refers to the

effect of false and/or missing R-peak detections.

siological R-peak and/or by imprecise ﬁducial point

localization provided by the automatic QRS detector.

The accuracy of the digitization depends on both the

sampling frequency and the resolution of the applied

electrocardiography (ECG) recorder. These effects are

illustrated in Figure 2. It is observed that the exact

location of the digitized R-peak is highly dependent

on a combination of the sampling frequency and the

resolution. This poses a clear risk of inducing jitter.

But jitter also depends on the ﬁducial points set by the

QRS detector. Jitter might also arise from artifacts in

the ECGs. Only a few studies have attempted to esti-

mate the inﬂuence of the introduced jitter (Tapanainen

et al., 1999) and most of them are primarily focused

on the inﬂuence of the sampling frequency (García-

González et al., 2004; Ziemssen et al., 2008). Only

very limited knowledge is available about the inﬂuence

of the overall amount of jitter. There are thus several

unanswered questions related to the necessary prere-

quisites for reliable estimation of clinically relevant

HRV measures. The focus of this study is therefore to

provide new knowledge about the required minimum

conditions that permit reliable estimation of clinically

relevant HRV measures and a method capable of as-

sessing whether or not these conditions are met.

2 METHODS

In (AHA and ESC, 1996) it is suggested that HRV

measurement systems should be tested using simu-

lated RR series with known HRV properties. One of

the downsides to this approach is the lack of physio-

Figure 2: Illustration of the potential issues with imprecise

digitization of the true physiological R-peak position. (a)

Raw ECG snippet with indication of the most important

ECG ﬁducial points. The red mark on top of the second

QRS complex indicates the area that is zoomed in on in (a)

and (b). (a) and (b) illustrate the inﬂuence of different bit

resolutions and different sampling frequencies, respectively.

The recorded reference curve is the blue line (16 bit, 1024

Hz), and the other curves are simulations based on the blue

line.

logical relevance in the simulated signals. This fact is

demonstrated by (Smith et al., 2002). Their method

automatically classiﬁes an RR series as synthetic or

physiological. It yielded a 100% accuracy when eval-

uated on a Physionet/Computing in Cardiology 2002

challenge dataset. Hence, validation of HRV system

using synthetic RR series as a basis may not be relevant

for physiological ECG signals. Therefore, we suggest

an alternative approach avoiding synthetic data.

A method that is very popular in the literature re-

garding signal averaged ECG (Fonseca et al., 2014;

Shaw and Savard, 1995) is used to obtain the physi-

ologically true R-peak locations. In contrast to simu-

lated RR series, this data will contain relevant physio-

logical content. The method obtains the true R-peak

locations from raw ECG and QRS ﬁducial points. The

true R-peak locations can then be used to calculate the

jitter of an HRV measurement system. The jitter is

deﬁned as the standard deviation of the differences be-

tween the true R-peak locations and the ﬁducial points

given by the system. Furthermore, physiologically true

HRV measures based on the true RR series can be used

to calculate the error of the HRV measurement system.

Investigation of the Minimum Conditions for Reliable Estimation of Clinically Relevant HRV Measures - Introducing a Novel Approach to

the Validation of HRV Measurement Systems

The method is then applied to Physionet’s ’Normal

Sinus Rhythm Database’ in order to obtain physiolog-

ically true RR series with the locations of abnormal

beats annotated as well. From the true RR series analy-

ses of the effects of jitter and appropriate handling of

abnormal beats, as well as missed and false detections

are performed.

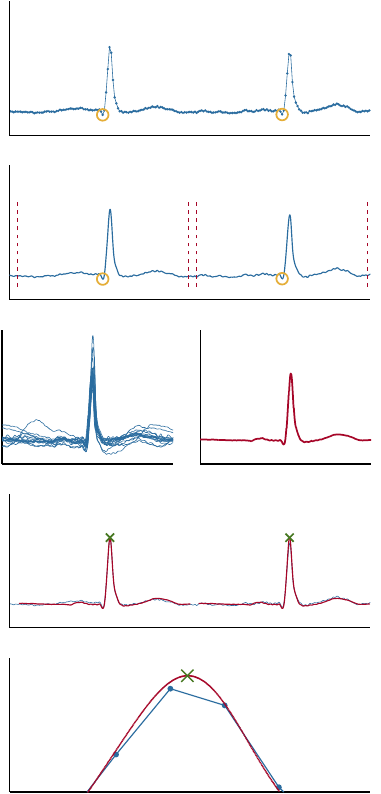
2.1 Obtaining the True RR Series

This section describes the cross correlation-based tem-

plate matching algorithm. Baseline drift of the raw

ECG is removed by ﬁltration with a Kaiser window

ﬁnite impulse response high-pass ﬁlter with a cut off

frequency at 0.67 Hz. An example of input to the tem-

plate matching algorithm is shown in Figure 3(a). The

initial ﬁducial points could be manual annotations or

output from an automatic QRS detector. Selected illus-

trative stages of the algorithm are shown in Figure 3

and the algorithm is deﬁned by the following steps.

Interpolate the ECG signal such that the sampling

frequency is increased to

= 8192

Hz. See

Figure 3(b).

Extract a window of length equal to the median

heartbeat interval around each of the current ﬁdu-

cial points. See Figures 3(b) and 3(c).

Calculate the template deﬁned as the mean of the

extracted windows. See Figure 3(d).

Calculate the cross correlation between the ECG

signal around the estimated R-peak locations and

the template. The sample index of the maxi-

mum cross correlation values is applied to improve

the estimation of the R-peak location. These R-

peak location estimations serve as the new ﬁducial

points. See Figure 3(e).

5. Repeat steps 2.–4. once more.

Repeating steps 2.–4. a third time did not change the

outcome. The output is compared with the input in

Figure 3(f). The location of the physiologically true

R-peak is deﬁned by the template maximum (green

cross). Note that it is located between the original

samples of the raw ECG.

Interpolation.

The database is sampled at 128 Hz.

Since the frequency content of the QRS complex falls

below half of this sampling frequency, the Shannon-

Nyquist sampling theorem tells us that the signal can

be reconstructed for all time by bandlimited interpo-

lation (Dodson, 1992; Proakis and Monolakis, 1996;

Bashir et al., 2010). Therefore, the interpolation in

step 1 is performed by bandlimited interpolation.

(a)

(b)

(e)

(f)

Figure 3: Illustration of the template matching algorithm

described in section 2.1. (a) shows the ECG after removal of

baseline drift, and manually annotated QRS complex ﬁdu-

cial points. (b) shows the interpolated ECG with ﬁducial

points. The windows extracted in step 2 are marked by red,

dotted lines. (c) shows examples of windows of interpolated

ECG extracted in step 2. (d) shows the mean of the extracted

windows of the interpolated ECG. This is the initial ECG

template. (e) shows the interpolated ECG, and the initial

template at the locations of maximal cross correlation. The

template maximum is marked. It represents the result after

steps 2.–4. have been executed once. These results serve

as input when repeating the steps 2.–4. (f) shows a com-

parison between the original data and the algorithm output.

The template (red line) and the physiologically true R-peak

position (green cross) is shown along with the original raw

ECG (blue line). Each blue dot indicates the location of one

of the original samples. Note that the true R-peak position

deﬁned by the algorithm is in between two of the original

samples.

CARDIOTECHNIX 2015 - International Congress on Cardiovascular Technologies

In (Fonseca et al., 2014) a post-processing algo-

rithm for precise R-peak location without the use of

interpolation is introduced. However, the template

matching algorithm is also used in (Fonseca et al.,

2014) as a “golden standard” and is thus preferred

here.

2.2 HRV Measures

For this study HRV measures from both the time

(SDNN, RMSSD, pNN50, SDI), frequency (LF/HF,

VHF), geometric (

SD1SD2), and non-linear domain

was chosen (ApEn, SampEn).

SDNN is the standard deviation of all normal-to-

normal (NN) intervals. RMSSD is the root-mean-

square of the differences between successive NN-

intervals. pNN50 is the percentage of differences

between successive NN-intervals that are larger than

50 ms. SDI is the mean of all SDNN calculated over

5 minute intervals across a long-term recording.

The following ranges are used for frequency do-

main analysis: Very low frequency (VLF) [0.003,

0.04], low frequency (LF) [0.04, 0.15], high frequency

(HF) [0.15, 0.4], and very high frequency (VHF) [0.4,

0.5]. The frequency spectrum was obtained both by

Lomb-Scargle (L-S) periodogram and Fourier trans-

formation of the RR time series equidistantly sampled

at 4 Hz by using cubic spline interpolation. The L-S

periodogram has the beneﬁt of not requiring an equidis-

tantly sampled time series.

SD1 is the standard deviation of the distances of the

points of the Poincaré plot projected onto the identity

line (x=y) and is related to short-term HRV. SD2 is

the standard deviation of the distances of the points of

the Poincaré plot projected onto the line perpendicular

to the identity line and is related to long-term HRV.

SD1SD2 is calculated as

π ·SD1 ·SD2

and measures

the overall variability.

Approximate entropy (AnEn) quantiﬁes the unpre-

dictability of ﬂuctuations in the RR series. Sample

entropy (SampEn) is a reﬁned version of approximate

entropy (Richman and Moorman, 2000).

2.3 Jitter Simulation

To investigate the effects of jitter a simulation of jit-

ter is executed. Physionet’s ‘Normal Sinus Rhythm

database’ (Goldberger et al., 2000) contains both the

raw ECG signals and annotations of 21 subjects and

serves as a basis for the simulation. The physiolog-

ically true R-peak locations are found via the auto-

matic template matching algorithm applied to the QRS

complex ﬁducial points marked in the annotation ﬁles.

In some areas the Normal Sinus Rhythm Database

Table 1: Optimal jitter values assuming smallest possible

jitter within the given sampling frequency. Average of jitter

values for the Pan-Tompkins algorithm for the ﬁrst two hours

of the selected subjects of the dataset. Some subjects of the

dataset were excluded because of wrongful annotations in

the corresponding annotation ﬁles.

(Hz) Optimal jitter (ms) Pan-Tompkins jitter (ms)

128 2.3 8.8

256 1.1 4.3

512 0.6 1.8

1024 0.3 0.7

has marked normal QRS-complexes as being ‘QRS-

like artifacts’. We corrected this manually in order to

obtain RR series free of any technical errors and ex-

cluded some subjects because of wrongful annotations.

The RR series were detrended by a method based on

smoothness priors (Tarvainen et al., 2002).

It is assumed that the jitter is normally distributed.

Thus, the jitter simulation is carried out by adding

random numbers drawn from the normal distribution

to the true R-peak locations using a random number

generator in MATLAB

(Mersenne Twister). This

means that the simulation will only be exact for HRV

systems that show the same pattern in their differences

from the true R-peak locations. The simulation is run

with increasing jitter values and it is repeated ten times

for each jitter value. For each run relative accuracy

error (RAE) is calculated as

RAE =

|s −s

true

·100%, (1)

for each estimated HRV measure

and ground true

HRV measure s

true

. Finally the average RAE is calcu-

lated over the ten runs at each level of jitter.

Minimum Jitter.

Let the jitter be deﬁned as the stan-

dard deviation of the localization errors of the R-peak

ﬁducial points. Assume that the true RR series is

known. Let the ECG signal be sampled at ﬁnite sam-

pling frequency

. Theoretical jitter values can then

be calculated assuming that the R wave ﬁducial point

localization was ideal within the respective sampling

frequency. The error will then be uniformly distributed

[0,1/ f

[

and the standard deviation equals (Kellogg,

1996)

1/ f

√

. (2)

The jitter values given in Table 1 are found via this

formula. It must be emphasized that these values re-

present best case scenarios.

Jitter of the Pan-Tompkins Algorithm. An imple-

mentation of the Pan-Tompkins QRS detector (Pan and

Investigation of the Minimum Conditions for Reliable Estimation of Clinically Relevant HRV Measures - Introducing a Novel Approach to

the Validation of HRV Measurement Systems

Tompkins, 1985) was tested on the data and compared

to the ground truth. The different sampling frequen-

cies were obtained by interpolation. This revealed the

jitter values shown in the last column of Table 1. The

values are much higher than the minimum values. The

differences between the physiological truth and the

ﬁducial points given by Pan-Tompkins were normally

distributed, hence the output of the later described

jitter simulation is accurate for this algorithm.

Handling Abnormal Heartbeats.

Ectopic beats do

not originate from the sinoatrial node, and the effect

of these should therefore be minimized or eliminated

when calculating the HRV measures. The abnormal

beats (e.g. ectopic beats) are marked in the annota-

tions ﬁle. From this information an investigation on

the effect of adjusting the respective RR time events

(outliers) versus leaving the RR series unaltered for

both short-term and long-term HRV was performed.

For time series analysis the outliers were deleted

prior to calculation of the HRV measures. For fre-

quency spectrum analysis, the outliers were replaced

by cubic spline interpolation when calculating the

equidistantly sampled RR series. For geometric and

nonlinear measures the outliers were replaced using

cubic spline interpolation.

Missed & False Detections.

Missed and false QRS

detections are simulated by extracting a random 5

minute RR series free of abnormal beats from each

subject and randomly removing or adding an extra

beat. The added beat is restricted to not being closer

than 250 ms to any neighboring beat. This simulates

a refractory period typically implemented in an au-

tomatic QRS detector. Automatic outlier detection

and replacement methods for manipulation of the RR

series can be found in e.g. (Kemper et al., 2007).

3 RESULTS & DISCUSSION

3.1 Jitter

Subsets of the results of the short-term and long-term

HRV jitter simulations are shown in Figure 5 and 6,

respectively. Figure 4 explains how Figure 5 and 6

should be read. The short-term HRV error is calculated

as the mean error of the HRV measures of 5-minute

segments selected randomly as the beginning of each

of the ﬁrst ten hours of the recordings which all start

before noon, yielding a total of ten segments for each

subject. For each chosen subject and HRV measure

the average relative accuracy error (RAE) is shown as

RAE (%)

QRS jitter (ms)

2 3 4 5 6 7 8 9 10

Figure 4: This ﬁgure and text explains how Figures 5 and 6

should be read. The blue vertical lines represent minimum

(which also means optimal) jitter values at sampling frequen-

cies 1024, 512, 256, and 128 Hz from left to right. The ma-

genta lines represent jitter values of the tested Pan-Tompkins

algorithm at the same sampling frequencies and illustrates

that the jitter at various sampling frequencies depends on the

QRS detector. Note that each sampling frequency is illus-

trated by a distinct line style. It is apparent that the relative

accuracy error (RAE) does not only depend on sampling

frequency, but on the system as a whole. On Figures 5 and 6

the lines marking the Pan-Tompkins algorithm performance

are left out. The acceptable level of RAE will be application

dependent. This graph shows the jitter simulation output of

one HRV measure (HF) for a subset of subjects from the

database. Only eight subjects are included in this illustrative

graph for the sake of clarity. A large inter-subject variability

is seen. Furthermore, it is seen that the relative accuracy

error (RAE) increases as the jitter increases.

a function of increasing jitter. The minimum jitter at

sampling frequencies 1024, 512, 256 and 128 Hz is

shown as the blue lines from left to right. Figures 5(a)

and 6(a) show the measured jitter of the tested im-

plementation of the Pan-Tompkins algorithm as the

magenta lines. This illustrates that the jitter does not

only depend on the choice of sampling frequency but

of many other factors, one being the performance of

the QRS detector.

In general, the results of the two simulations are

quite close to each other. However, the curves of the

long-term simulation are smoother. This is probably

because of the simulated noise is randomly chosen

from the normal distribution. Longer segments will

create empirical distributions quite close to the normal

distribution, while shorter segments might not. This

illustrates how the instability of a system can have a

greater impact on HRV analysis on shorter segments.

There are large interpersonal variations in the relative

accuracy errors (RAE) for all simulations.

A HRV measure like pNN50 can quite quickly

have a large RAE since the respective NN50 count

can e.g. be equal to 1 and adding e.g. 1 more as a

CARDIOTECHNIX 2015 - International Congress on Cardiovascular Technologies

result of noise can then double the RAE. This shows

that conclusions based on pNN50 should be made with

care, especially for short-term HRV, see Figures 5(c)

and 6(c).

The jitter induced changes in the LF/HF measure

are dominated by HF. LF, VLF, and ULF are quite

stable in regards to jitter as could be expected. Since

HF is overestimated at higher levels of jitter, LF/HF

is underestimated as a result, see Figures 5(b), 6(b),

and 6(d). VHF is affected to a greater degree by jit-

ter than HF, which shows that jitter induced by e.g.

lower sampling frequency adds high frequency noise

— the higher the frequencies in question the greater

the error, see Figure 5(d). Frequency domain mea-

sures based on L-S periodogram and Fourier transfor-

mation were strikingly similar as illustrated by Fig-

ures 6(d) and 6(b). This was surprising since the L-

S method does not require the step of obtaining an

equidistantly sampled RR series. The error in the

measure

SD1SD2 is dominated by SD1 measuring

short-term variability and will be overestimated as a re-

sult of jitter, see Figures 5(g) and 6(g). It is thought by

some to give a better estimate of the overall variability

as compared to SDNN, but it is not as stable in regards

to jitter, see Figures 5(a) and 6(a). SDI is as stable

as SDNN, which could be expected, see Figure 6(f).

RMSSD is very similar to

SD1SD2 in the way that

it is calculated and thus not surprisingly also in jitter

sensitivity, see Figure 6(e).

Sampling Frequency.

It is interesting to note that in-

ducing jitter, e.g. by lowering the sampling frequency,

will have the effect of overestimating most of the HRV

measures. This means that a perfect QRS detector will

potentially be able to detect the high frequency ﬂuc-

tuations of the HRV measures with greater accuracy

at higher sampling frequencies, and inducing jitter by

lowering the sampling frequency and/or decreasing the

localization accuracy of the QRS detector can result

in overestimation of the HRV measures designed to

measure high frequency ﬂuctuations.

As discussed, the jitter might originate from several

different factors (e.g. low bit resolution, low sampling

frequency, artefacts, and low QRS localization accu-

racy). These factors are mutually inﬂuencing each

other, and it is thus difﬁcult to provide a deﬁnitive

conclusion on the required sampling frequency inde-

pendently of all other factors in the HRV measurement

system. We therefore recommend that the cumulative

effect from all factors are investigated when choosing

the sampling frequency.

Abnormal Heartbeats.

Table 2 on page 9 shows

the average plus/minus the standard deviation of the

relative accuracy error for all subjects. It is clear that

the effect of not correcting the abnormal beats in the

short-term HRV can be quite severe. The long-term

analysis is more robust for this type of error with a

maximum value of 2%. This suggests that when per-

forming short-term HRV analysis on healthy subjects

biological errors need to be addressed. However, for

long-term analysis on this dataset the effects of abnor-

mal beats are deemed to be insigniﬁcant.

Missed & False Detections.

The effects of a missed

detection are higher than that of a false detection, see

Table 2. It is interesting to see that a missed detection

also has a profound effect on LF, while a false detec-

tion has much less. Overall the errors are very high

except for the HRV measure meanNN. It is clear that

such an error will have a much more serious negative

effect on the HRV measures than the choice of lower

sampling frequency of e.g. 128 Hz. This can also be

observed on SDNN which proved to be very stable

when higher levels of jitter were applied.

Comparison with Existing Literature.

(Ziemssen et al., 2008) the EUROBAVAR data set,

sampled at 500 Hz, is downsampled to 200 Hz

and 100 Hz. Only ultra high frequency (deﬁned by

frequencies

> 40

Hz) was signiﬁcantly different when

comparing the values across the different sampling

frequencies. This is comparable to our results, where

VHF shows larger errors than LF/HF at the same jitter

levels, see Figure 5. In (AHA and ESC, 1996) it is

recommended to use RMSSD instead of pNN50, since

it has better statistical properties. In (Hejjel and Roth,

2004) the authors ﬁnd that pNN50 is very unreliable

even at jitter levels of 1 ms. This is also supported by

our results.

4 CONCLUSION

We recommend that each HRV measurement system

should be validated by

1. showing low jitter levels, and/or

the HRV measures that it produces should be com-

pared with and be close to the ones obtained by the

template matching method described in this study.

This method will allow HRV systems to be tested with-

out the need for synthetic signals or comparison with

a different system recording simultaneously. It only

requires access to the recorded ECG signal.

In this study it was found that handling abnormal

beats was important for short-term HRV analysis, but

Investigation of the Minimum Conditions for Reliable Estimation of Clinically Relevant HRV Measures - Introducing a Novel Approach to

the Validation of HRV Measurement Systems

(a) SDNN

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(b) LF/HF

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(d) VHF

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(e) ApEn

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(f) SampEn

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(g) π

π SD1SD2

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

19090

18184

18177

17453

17052

16795

16786

16773

16539

16483

16420

16273

16265

Figure 5: Jitter simulations based on short-term HRV measures. The average relative accuracy error (RAE) is shown as a

function of jitter for different subjects. The blue lines correspond to minimal possible jitter at sampling frequencies 1024, 512,

256, and 128 Hz from left to right. (a) also shows the jitter of the Pan-Tompkins algorithm — note the matching line styles

between the sampling frequencies. The subject identiﬁcation numbers are shown in the legend.

CARDIOTECHNIX 2015 - International Congress on Cardiovascular Technologies

(a) SDNN

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(b) LF/HF

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(d) LF/HF (L-S)

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(e) RMSSD

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(f) SDI

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

(g) π

π SD1SD2

RAE (%)

Jitter (ms)

2 3 4 5 6 7 8 9 10

19090

18184

18177

17453

17052

16795

16786

16773

16539

16483

16420

16273

16265

Figure 6: Jitter simulations based on long-term HRV measures. The average relative accuracy error (RAE) is shown as a

function of jitter for different subjects. The blue lines correspond to minimal possible jitter at sampling frequencies 1024, 512,

256, and 128 Hz from left to right. (a) also shows the jitter of the Pan-Tompkins algorithm — note the matching line styles

between the sampling frequencies. The subject identiﬁcation numbers are shown in the legend.

Investigation of the Minimum Conditions for Reliable Estimation of Clinically Relevant HRV Measures - Introducing a Novel Approach to

the Validation of HRV Measurement Systems

Table 2: Average plus/minus standard deviation of relative approximation error in percent for both abnormal beats, false and

missed detections.

meanNN SDNN RMSSD pNN50 HF LF π SD1SD2

Abnormal beat

Long-term 0.0 ±0.0 0.1 ±0.1 0.6 ±0.6 0.2 ±0.4 0.4 ±0.5 0.1 ±0.1 0.5 ±0.6

Short-term 0.0 ±0.0 1.6 ±1.7 11.6 ±11.1 7.6 ±14.6 14.1 ±15.2 4.1 ±8.0 12.4 ±11.3

False detection

Short-term 0.2 ±0.0 7.9 ±7.0 53.7 ±51.2 15.5 ±13.8 85.1 ±124.1 6.0 ±4.6 64.0 ±62.5

Missed detection

Short-term 0.2 ±0.0 15.8 ±17.6 128.7 ±102.7 11.8 ±10.9 657.6 ±1119.7 83.8 ±91.9 158.9 ±155.0

not for long-term HRV. It was found that missed and

false detection had a severe effect on short-term HRV.

We cannot deﬁne a limit for acceptable jitter levels

because it will depend on the analysis carried out in

each the speciﬁc study.

This investigating was carried out using ECG from

healthy subjects. The results are therefore limited to

studies using healthy subjects. Analysis of subjects

with lower HRV measures might result in larger rela-

tive errors at the same levels of jitter.

REFERENCES

Bashir, M., Lee, D., Akasha, M., Yi, G., Cha, E., Bae, J., Cho,

M., and Ryu, K. (2010). Highlighting the current issues

with pride suggestions for improving the performance

of real time cardiac health monitoring. Information

Technology in Bio-and Medical Informatics, ITBAM

2010, pages 226–233.

ESC and NASPE (1996). Guidelines Heart rate variability.

European Heart Journal, pages 354–381.

Citi, L., Brown, E. N., and Barbieri, R. (2012). A real-time

automated point-process method for the detection and

correction of erroneous and ectopic heartbeats. IEEE

Transactions on Biomedical Engineering, 59(10):2828–

2837.

Dodson, M. (1992). Shannon’s Sampling Theorem. Current

Science, 63(5):253 – 260.

Fonseca, P., Aarts, R. M., Foussier, J., and Long, X. (2014).

A novel low-complexity post-processing algorithm for

precise QRS localization. SpringerPlus, 3(1):376.

García-González, M. a., Fernández-Chimeno, M., and

Ramos-Castro, J. (2004). Bias and uncertainty in

heart rate variability spectral indices due to the ﬁnite

ECG sampling frequency. Physiological measurement,

25(2):489–504.

Goldberger, A., Amaral, L., Glass, L., Hausdorff, J., Ivanov,

P., Mark, R., Mietus, J., Moody, G., Peng, C.-K.,

and Stanley, H. (2000). PhysioBank, PhysioToolkit,

and PhysioNet: Components of a New Research Re-

source for Complex Physiologic Signals. Circulation,

101(23):e215–e220.

Hejjel, L. and Roth, E. (2004). What is the adequate sam-

pling interval of the ECG signal for heart rate vari-

ability analysis in the time domain? Physiological

measurement, 25(6):1405–1411.

Huikuri, H. V. and Stein, P. K. (2013). Heart rate variability

in risk stratiﬁcation of cardiac patients. Progress in

Cardiovascular Diseases, 56(2):153–159.

Kellogg, B. (1996). CRC Standard Mathematical Tables and

Formulae (Daniel Zwillinger, ed.).

Kemper, K. J., Hamilton, C., and Atkinson, M. (2007). Heart

rate variability: Impact of differences in outlier identi-

ﬁcation and management strategies on common mea-

sures in three clinical populations. Pediatric Research,

62(3):337–342.

Pan, J. and Tompkins, W. J. (1985). A real-time QRS de-

tection algorithm. IEEE transactions on bio-medical

engineering, 32(3):230–236.

Proakis, J. G. and Monolakis, D. G. (1996). Digital Signal

Processing: principles, algorithms and applications.

Richman, J. S. and Moorman, J. R. (2000). Physiological

time-series analysis using approximate entropy and

sample entropy. American journal of physiology. Heart

and circulatory physiology, 278(6):H2039–H2049.

Shaw, G. R. and Savard, P. (1995). On the detection of

QRS variations in the ECG. IEEE Transactions on

Biomedical Engineering, 42(7):736–741.

Smith, F. E., Bowers, E. J., Langley, P., Allen, J., and Murray,

A. (2002). Heart rate variability characteristics required

for simulation of interval sequences. In Computers in

Cardiology, volume 29, pages 237–240.

Tapanainen, J. M., Seppänen, T., Laukkanen, R., Loimaala,

A., and Huikuri, H. V. (1999). Signiﬁcance of the

accuracy of RR interval detection for the analysis of

new dynamic measures of heart rate variability. Annals

of Noninvasive Electrocardiology, 4(1):10–18.

Tarvainen, M. P., Ranta-Aho, P. O., and Karjalainen, P. A.

(2002). An advanced detrending method with appli-

cation to HRV analysis. IEEE transactions on bio-

medical engineering, 49(2):172–5.

Ziemssen, T., Gasch, J., and Ruediger, H. (2008). Inﬂuence

of ECG sampling frequency on spectral analysis of

RR intervals and baroreﬂex sensitivity using the EU-

ROBAVAR data set. Journal of Clinical Monitoring

and Computing, 22(2):159–168.

CARDIOTECHNIX 2015 - International Congress on Cardiovascular Technologies