The NOESIS Open Source Framework for Network Data Mining
V
´
ıctor Mart
´
ınez, Fernando Berzal and Juan-Carlos Cubero
Department of Computer Science and Artificial Intelligence, University of Granada, Granada, Spain
Keywords:
Network Analysis, Network Visualization, Community Detection, Structural Properties.
Abstract:
NOESIS is a software framework for the development of data mining techniques for networked data. As an
open source project, released under a BSD license, NOESIS intends to provide the necessary infrastructure for
solving complex network data mining problems. Currently, it includes a large collection of popular network-
related data mining techniques, including the analysis of network structural properties, community detection
algorithms, link scoring and prediction methods, and network visualization techniques. The design of NOESIS
tries to facilitate the development of parallel algorithms using solid object-oriented design principles and
structured parallel programming. NOESIS can be used as a stand-alone application, as many other network
analysis packages, and can be included, as a lightweight library, in domain-specific data mining applications
and systems.
1 INTRODUCTION
In some application domains, classical data mining
is giving way to relational data mining, where data
sets contain interacting or connected elements. Re-
lational data brings new research and development
opportunities. In this context, network data mining
techniques are being developed to analyze relational
data. Network-based techniques include a large num-
ber of theoretical models, algorithmic methods, and
pragmatic techniques that exploit the topology of net-
works, as well as node and link attributes. The anal-
ysis of networks has a large number of applications
in a wide range of fields. For instance, social net-
work analysis is used to discover the structure of so-
cial networks, where users can interact in many dif-
ferent ways. In biology, network analysis techniques
have been applied to protein-protein interaction net-
works and metabolic networks to achieve a better un-
derstanding of their underlying entities and perform
predictions about their behavior. Network analysis
techniques also have applications in logistic, commu-
nication, and transportation networks, among others.
Many tools have been developed to perform net-
work analysis. These tools typically allow the visu-
alization of network data in a convenient way, facili-
tating the visual exploration of relational data. Tools
and frameworks that have attained some popularity
include Pajek (Batagelj and Mrvar, 1998), NodeXL
(Smith et al., 2009), Cytoscape (Shannon et al., 2003),
and Gephi (Bastian et al., 2009). Each of these tools
has its own strengths and weaknesses. The main
weaknesses of some of these tools include hard-to-use
user interfaces, limited sets of analysis techniques,
limited execution platforms, or a design that makes
it difficult their incorporation in larger data mining
projects (when they are not completely closed for ex-
tension). Quite often, networks analysts rely on mul-
tiple of these tools to perform tasks that could be car-
ried more easily in a single integrated platform.
In order to improve this situation, we have started
the development of NOESIS, a lightweight, yet pow-
erful, network analysis software framework. NOE-
SIS, which stands for Network-Oriented Exploration,
Simulation, and Induction System, is 100% Java and
has been released under a BSD open source license.
NOESIS includes the implementation of a large num-
ber of algorithmic techniques that address different
aspects of networks analysis, including network vi-
sualization (Herman et al., 2000) (Tamassia, 2013),
the analysis of network structural properties (Wasser-
man and Faust, 1994) (Newman, 2010), community
detection (Fortunato, 2010), and link scoring and pre-
diction (Liben-Nowell and Kleinberg, 2007). NOE-
SIS also provides a minimalistic clean graphical user
interface that allows the drag & drop manipulation
of networks, the execution of network analysis tech-
niques and the visualization of results. In addition,
NOESIS can be used as a third-party software library
in larger projects.
This paper introduces NOESIS and is structured
as follows. First, we will describe the software de-
316
Martínez, V., Berzal, F. and Cubero, J..
The NOESIS Open Source Framework for Network Data Mining.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 1: KDIR, pages 316-321
ISBN: 978-989-758-158-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

sign decisions that have shaped the architectural de-
sign of NOESIS. In the following section, we will
mention some of the network data mining techniques
that NOESIS currently implements. Finally, we will
conclude our paper with some pointers to the future
of the NOESIS open source software project.
2 SOFTWARE ARCHITECTURE
NOESIS is being developed following some clear de-
sign guidelines. It has been designed to be maintain-
able, reusable, and extensible. NOESIS strongly re-
lies on abstract interfaces and independent modules
to achieve strong cohesion and loose coupling. The
use of the SOLID object-oriented design principles
(Martin, 2003) facilitates the implementation of new
features as independent modules with a minimal set
of dependencies.
Figure 1: The NOESIS system architecture.
The overall architecture of the NOESIS frame-
work is shown in Figure 1. Different NOESIS sub-
systems address specific aspects that must be taken
into account in the development of component-based
data mining frameworks (Berzal et al., 2002).
The core of the NOESIS system is a reflective
kernel. Within the kernel, programmers can pro-
vide the implementation of models and tasks that ex-
ecute data mining algorithms on models. Models re-
fer to the data structures needed to represent differ-
ent kinds of networks as well as the representation of
data mining results themselves. A large collection of
network-related data mining techniques, which will
be described later, has already been implemented as
NOESIS tasks. The extensive use of abstract inter-
faces allows switching from one implementation to
another with a minimal cost, therefore facilitating ex-
perimentation. Object-oriented design patterns facili-
tate the development of new techniques and custom-
tailored solutions to specific data mining problems.
For example, the visitor design pattern enables the
efficient and widespread reuse of network traversal
techniques, such as breadth-first search (BFS) and
depth-first search (DFS). This basic graph algorithms
can be reused, for instance, to easily compute the be-
tweenness of nodes and links, a centrality measure
employed by some community detection algorithms.
The execution of tasks in the NOESIS kernel re-
lies on the hardware abstraction layer (HAL). One
of the main features that makes NOESIS stand apart
from other network analysis packages is that it en-
courages the use of structured parallel programming
through an easy-to-use library. Our library enables the
implementation of parallel algorithms that can exploit
the multiple cores of current microprocessors and it
does so without imposing an unnecessary burden on
the shoulders of algorithm designers and developers,
who can focus on their algorithm details without be-
ing overwhelmed by the underlying execution frame-
work. Eventually, this hardware abstraction layer will
also provide a transparent mechanism for the execu-
tion of data mining tasks in completely distributed
systems, not just multiprocessors.
The data access layer is the NOESIS subsystem
that is responsible for providing access to data from
different data sources. Different standard network file
formats are supported, including GML, GraphML,
and GDF.
• GML (Graph Modeling Language) is a portable,
simple, and flexible text-based file format used
by Graphlet, Pajek, yEd, LEDA, and NetworkX.
GML files contain hierarchical key-value lists that
allow the definition of arbitrary properties for
nodes and links.
• GraphML is an XML-based file format sup-
ported by NodeXL, Sonivis, GUESS and Net-
workX. This format supports different kinds of
networks, including directed, undirected, mixed,
hypergraphs, and hierarchical networks.
• GDF is also a text-based file format, initially
used by the GUESS tool, whose structure is very
similar to the comma separated value file format
(CSV) and where each network element is repre-
sented by a text line and its properties are sepa-
rated by commas.
For experimentation during the development of
network data mining techniques, synthetic data sets
The NOESIS Open Source Framework for Network Data Mining
317

are also useful. NOESIS also implements some net-
work models, from regular networks to different kinds
of random networks. Researchers have devised the-
oretical network models to provide insight on how
real networks are formed and behave. Network for-
mation models are theoretical models that allow us
to generate networks with some specific properties
by following well-defined mechanisms (Albert and
Barab
´
asi, 2002). These models are used to gen-
erate networks with similar properties to real net-
works (and artificial networks with the desired prop-
erties). NOESIS includes network generators for
Erd
¨
os-R
´
enyi and Gilbert random networks, Watts–
Strogatz small world networks, Barab
´
asi–Albert pref-
erential attachment networks, and Price’s citation net-
works, among other variations of random networks
that might be of interest for those studying the be-
havior of network analysis techniques. Regular net-
works, such as complete networks, star networks, ring
networks, tandem networks, mesh networks, toroidal
networks, hypercube networks, and tree networks, are
also included, since they are often useful during the
development of new algorithms. For instance, they
can be used in unit tests when following a test-driven
development approach.
The current version of NOESIS is provided as a
lightweight JAR package (around 1 MB) and has no
external software dependencies, so it can be easily
incorporated in other software development projects.
It can be downloaded from the NOESIS project web
page at http://noesis.ikor.org/.
For less-advanced users, NOESIS also provides
a graphical user interface, similar to the interface
provided by other network analysis packages such
as Gephi, Pajek, or NodeXL. The NOESIS network
analyzer user interface is built using model-driven
software development techniques and is based on an
application generator that hides much of the detail
needed by the implementation of modern GUIs, thus
making it easy to modify and extend the tool to meet
the requirements of different data mining projects.
3 DATA MINING TECHNIQUES
NOESIS includes a wide range of network analysis
methods and techniques, including the computation
of network structural properties, the detection of com-
munities, and link scoring and prediction, as well as
different graph drawing techniques that help users vi-
sualize network data.
Figure 2: An international trade network. Color indi-
cates fish exports in 1998 (top countries: Thailand, Nor-
way, China, USA, Canada, Russia, Denmark, Indonesia,
Netherlands, Chile, Spain, UK). Size indicates betweenness
(top countries: Thailand, USA, Spain, Japan, Netherlands,
France, Italy, Germany, UK, Russia, Canada, Norway).
3.1 Network Structural Properties
Networks can be characterized by their structural or
topological properties. Network structural properties
allow us to measure specific aspects of the networks
and their elements, both nodes and links. A large
number of topological properties have been proposed
in the literature to measure different aspects of interest
(Jackson et al., 2008). The analysis of network struc-
tural properties allows us to understand the role each
node plays within a specific network and the struc-
tures that are present in the network.
NOESIS can be used to score network nodes ac-
cording to different criteria:
• Node degrees correspond to the number of con-
nections each node has within the network. In-
degrees, out-degrees, and total degrees are often
normalized according to network size. Biased and
unbiased degree assortativities measure the ten-
dency of nodes to be connected to other nodes
with similar degrees.
• Reachability scores measure how easily a node
can be reached from other nodes in the net-
work. Node eccentricity corresponds to the great-
est geodesic distance between a node and any
other node in the network. The maximum node
eccentricity is the network diameter, whereas the
minimum node eccentricity is its radius. The aver-
age path length is the average length of all shortest
paths starting from a given node. The closeness of
a node is the reciprocal of the sum of its distances
from all other nodes. Finally, decay is another
related measure that weights distances exponen-
tially and can be adjusted to approach degree or
component size, depending on our interests.
• Clustering coefficients evaluate the tendency of a
node neighbors to be connected between them, i.e.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
318
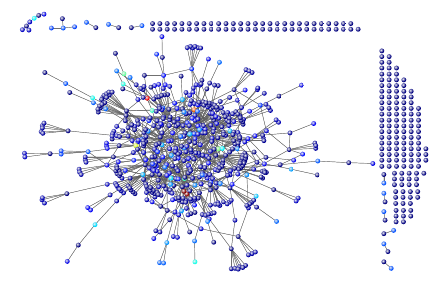
Figure 3: A Gnutella P2P file sharing network: Color indi-
cates PageRank.
how close its neighbors are to being a clique (a
complete graph).
• Betweenness-related properties quantify the num-
ber of times a node acts as a bridge along the
shortest path between two other nodes.
• The influence of each node within a network can
also be measured using other techniques that com-
pute the centrality of each node based on the
centrality of its neighbors. Google’s PageRank,
HITS, eigenvector centrality, Katz centrality, and
diffusion centrality belong to this group of mea-
sures.
Some of the aforementioned measures can also
be defined for network links rather than nodes. For
example, link betweenness computes the number of
shortest paths that pass through a specific link, link
embeddedness counts the number shared neighbors
between the nodes connected by a given link, and link
neighborhood overlap is a normalized version of link
embeddedness.
3.2 Community Detection Methods
The nodes of most real networks exhibit some kind of
community structure (Palla et al., 2005). Communi-
ties are densely-connected sets of nodes. Their iden-
tification is of great interest for understanding com-
plex networks and has many applications in different
fields such as biology or sociology. Given its impor-
tance, a large number of community detection algo-
rithms have been proposed (Lancichinetti and Fortu-
nato, 2009) (Fortunato, 2010), which differ in com-
putational and spatial complexity, as well as in their
ability to detect overlapping communities.
NOESIS implements a score of the most popu-
lar community detection methods. These methods
range from the mere detection of connected compo-
nents, which can be done in linear time, and heuris-
tic graph partitioning algorithms, to modularity-based
and spectral clustering techniques.
• Among graph partitioning techniques, the
Kernighan-Lin algorithm, with important ap-
plications in the layout of digital circuits and
components in VLSI, tries to minimize the
number of links crossing between communities.
• The Girvan-Newman is a hierarchical clustering
method that iteratively removes the links with the
highest betweenness. Radicchi’s algorithm is a
more efficient divisive hierarchical method that
resorts to link clustering coefficients based on the
idea that communities include a large number of
cycles but links between different communities
participate in less cycles. Agglomerative hierar-
chical techniques can also be used in networks
using different measures of distance and the typ-
ical variations of inter-cluster distance (namely,
single–linkage, average–linkage, and complete–
linkage).
• Modularity-based community detection methods
interpret community detection as an optimization
problem and several greedy heuristics have been
proposed.
• Spectral clustering techniques make use of the
spectrum (i.e. eigenvalues) of a similarity ma-
trix (e.g. the graph Laplacian) to perform dimen-
sionality reduction before clustering in fewer di-
mensions. For instance, spectral bisection (a.k.a.
EIG1) employs a single dimension, the one given
by the Fiedler vector, whereas the KNSC1 and
UKMEANS algorithms resort to the well-known
k-means clustering algorithm to cluster eigenvec-
tors.
• Some recent algorithms also support the detection
of overlapping communities. For instance, Big-
Clam (Yang and Leskovec, 2013) is an efficient
non-negative matrix factorization technique that
maximizes the log-likelihood of the detected com-
munities according to an affiliation graph model.
3.3 Link Scoring and Prediction
Link scoring and link prediction are two closely-
related tasks. Both tasks compute scores for pairs of
nodes, typically defined according to their similarity.
While link scoring computes the similarity for con-
nected pairs of nodes and can be used to rank existing
links, link prediction computes the similarity for un-
connected pairs of nodes and is mainly used to predict
new links, either links that will be created in the fu-
ture or existing links that are not currently observed
(L
¨
u and Zhou, 2011).
The NOESIS Open Source Framework for Network Data Mining
319
Link scoring and link prediction techniques can be
classified as local or global, depending on the amount
of information they consider for computing similari-
ties:
• Local techniques use only neighborhood infor-
mation to compute the similarity between a pair
of nodes, which makes them very efficient and
scalable, but are therefore limited to comput-
ing the similarities between nodes at distance
two. Many local link prediction techniques
are based on counting the number of shared
neighbors, such as the Adamic–Adar score and
the resource–allocation index, which penalize
each shared neighbor by its degree. Jaccard,
Salton, and S
¨
orensen scores use different normal-
ization strategies. The preferential–attachment
score is proportional to the product of the de-
gree of both nodes, which makes it suitable for
scale-free networks, whereas other local tech-
niques resort to different criteria (e.g. the lo-
cal Leicht–Holme–Newman, hub–promoted, and
hub–depressed scores).
• Global techniques consider the full topology of
the network, at a higher computational cost. The
Katz score is based on the number of exist-
ing paths between each pair of nodes, penalized
by their length, and the global Leicht–Holme–
Newman score is a similar method. Other global
methods are based on random walks (i.e. random
walk, random walk with restart, and flow propa-
gation) or the network Laplacian (e.g. pseudoin-
verse Laplacian score, average commute time, and
random forest kernel).
3.4 Network Visualization Techniques
Humans are currently better than machines at finding
and identifying visual patterns. Graph visualization
techniques place nodes following aesthetic guidelines
like spacing nodes according to their network dis-
tance, minimizing link crossings, or exposing prop-
erties like hierarchies or symmetry (Tamassia, 2013).
NOESIS includes different automatic graph lay-
out techniques, from a family of regular layout meth-
ods (for specific kinds of regular networks) to radial
and hierarchical layouts. It also includes the well-
known Fruchterman-Reingold and Kamada-Kawai
force-based layout algorithms, which simulate a phys-
ical system by setting attractive forces between pairs
of connected nodes (spring-like, based on Hooke’s
law) and repulsive forces between all pairs of nodes
(as electrically-charged particles, using Coulomb’s
law).
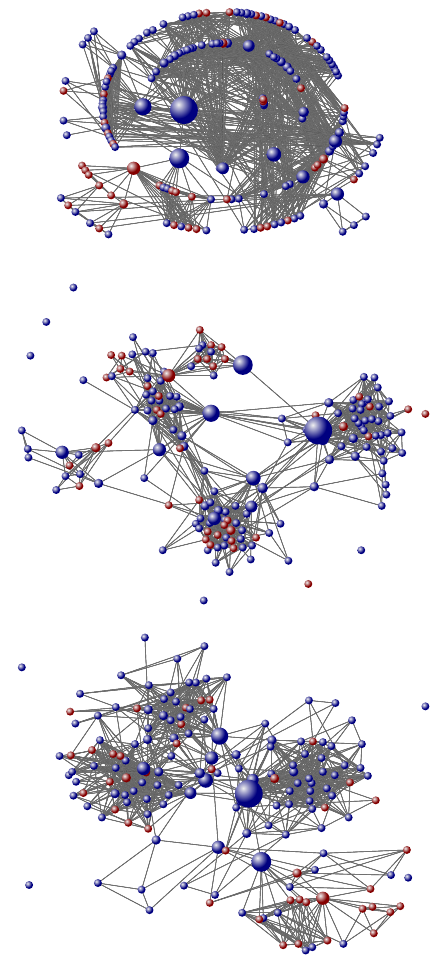
Figure 4: Different views of one of the authors’ Facebook
friendship network (from top to bottom): radial layout,
Fruchterman-Reingold layout, and Kamada-Kaway layout.
Node size indicates betweenness.
Beyond network layout, changing the visual style
and attributes of the network visualization is another
powerful tool for facilitating the interpretation of net-
work data, just by adjusting visual properties such as
node and link size, width, or color.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
320
4 CONCLUSIONS
In this paper, we have presented the NOESIS network
data mining framework. NOESIS is open source and
lightweight. It can be used as an stand-alone network
analysis tool, using the provided graphical user inter-
face, or as a reusable library in other software devel-
opment projects, since it is distributed under a permis-
sive BSD free software license. It is available at the
NOESIS project web page: http://noesis.ikor.org.
NOESIS algorithms are implemented using struc-
tured parallel programming patterns, which enable an
effective use of the available computing resources.
The framework is built on top of a hardware abstrac-
tion layer that provides parallelization mechanisms
and hides their underlying complexity. In the future,
it will let programmers execute their algorithms in a
fully distributed computing system, such as a server
farm or the cloud, in a fully-transparent way.
The NOESIS framework is evolving and new data
mining techniques are scheduled to be developed in
the future, from overlapping community detection
methods to quasi-local link scoring and prediction
techniques, as well as additional graph layout tech-
niques. Since the NOESIS graphical user interface is
based on a model-driven application generator, cre-
ating ports of the application generator to other plat-
forms, such as Android or the Web, will automatically
enable the use of the NOESIS GUI in those platforms.
NOESIS is in constant development and improve-
ment. Our goal is to provide the most complete open
source network data mining framework, while main-
taining its ease of use and hiding the complexity of the
underlying execution environment so that even non-
expert programmers can develop their own modules
and network analysis techniques.
ACKNOWLEDGEMENTS
This work is partially supported by the Spanish Min-
istry of Economy and the European Regional Devel-
opment Fund (FEDER), under grant TIN2012-36951,
and the Ministry of Education of Spain under the
program “Ayudas para contratos predoctorales para
la formaci
´
on de doctores 2013” (grant BES-2013-
064699). We are grateful to Aar
´
on Rosas, Francisco-
Javier Gij
´
on, and Julio-Omar Palacio for their contri-
butions to the implementation of community detec-
tion methods.
REFERENCES
Albert, R. and Barab
´
asi, A.-L. (2002). Statistical mechanics
of complex networks. Reviews of Modern Physics,
74(1):47.
Bastian, M., Heymann, S., Jacomy, M., et al. (2009). Gephi:
an open source software for exploring and manipulat-
ing networks. ICWSM, 8:361–362.
Batagelj, V. and Mrvar, A. (1998). Pajek-program for large
network analysis. Connections, 21(2):47–57.
Berzal, F., Blanco, I., Cubero, J.-C., and Marin, N. (2002).
Component-based data mining frameworks. Commu-
nications of the ACM, 45(12):97–100.
Fortunato, S. (2010). Community detection in graphs.
Physics Reports, 486(3):75–174.
Herman, I., Melanc¸on, G., and Marshall, M. S. (2000).
Graph visualization and navigation in information vi-
sualization: A survey. Visualization and Computer
Graphics, IEEE Transactions on, 6(1):24–43.
Jackson, M. O. et al. (2008). Social and economic networks.
Princeton University Press Princeton.
Lancichinetti, A. and Fortunato, S. (2009). Community de-
tection algorithms: a comparative analysis. Physical
Review E, 80(5):056117.
Liben-Nowell, D. and Kleinberg, J. (2007). The link-
prediction problem for social networks. Journal of the
American society for information science and technol-
ogy, 58(7):1019–1031.
L
¨
u, L. and Zhou, T. (2011). Link prediction in complex
networks: A survey. Physica A: Statistical Mechanics
and its Applications, 390(6):1150–1170.
Martin, R. C. (2003). Agile Software Development: Princi-
ples, Patterns, and Practices. Prentice Hall PTR.
Newman, M. (2010). Networks: An Introduction. Oxford
University Press.
Palla, G., Der
´
enyi, I., Farkas, I., and Vicsek, T. (2005).
Uncovering the overlapping community structure of
complex networks in nature and society. Nature,
435(7043):814–818.
Shannon, P., Markiel, A., Ozier, O., Baliga, N. S., Wang,
J. T., Ramage, D., Amin, N., Schwikowski, B., and
Ideker, T. (2003). Cytoscape: a software environment
for integrated models of biomolecular interaction net-
works. Genome research, 13(11):2498–2504.
Smith, M. A., Shneiderman, B., Milic-Frayling, N.,
Mendes Rodrigues, E., Barash, V., Dunne, C.,
Capone, T., Perer, A., and Gleave, E. (2009). Analyz-
ing (social media) networks with nodexl. In Proceed-
ings of the fourth international conference on Com-
munities and technologies, pages 255–264. ACM.
Tamassia, R. (2013). Handbook of graph drawing and vi-
sualization. CRC press.
Wasserman, S. and Faust, K. (1994). Social network analy-
sis: Methods and applications. Cambridge University
Press.
Yang, J. and Leskovec, J. (2013). Overlapping community
detection at scale: A nonnegative matrix factorization
approach. In Proceedings of the Sixth ACM Interna-
tional Conference on Web Search and Data Mining,
WSDM ’13, pages 587–596. ACM.
The NOESIS Open Source Framework for Network Data Mining
321
