FPGA Implementation of a Multi-Population PBIL Algorithm

ao Paulo Coelho

1,3

, Tatiana M. Pinho

2,3

and Jos

e Boaventura-Cunha

2,3

Instituto Polit

ecnico de Braganc¸a, Escola Superior de Tecnologia e Gest

ao,

Campus de Sta. Apol

onia, 5300-253 Braganc¸a, Portugal

Universidade de Tr

as-os-Montes e Alto Douro, UTAD, Escola de Ci

encias e Tecnologia,

Quinta de Prados, 5000-801 Vila Real, Portugal

INESC TEC Technology and Science, Campus da FEUP, 4200 - 465, Porto, Portugal

Keywords:

Population based Incremental Learning, Multi-Population Evolutionary Algorithms, FPGA.

Abstract:

Evolutionary-based algorithms play an important role in ﬁnding solutions to many problems that are not solved

by classical methods, and particularly so for those cases where solutions lie within extreme non-convex mul-

tidimensional spaces. The intrinsic parallel structure of evolutionary algorithms are amenable to the simulta-

neous testing of multiple solutions; this has proved essential to the circumvention of local optima, and such

robustness comes with high computational overhead, though custom digital processor use may reduce this

cost. This paper presents a new implementation of an old, and almost forgotten, evolutionary algorithm: the

population-based incremental learning method. We show that the structure of this algorithm is well suited to

implementation within programmable logic, as compared with contemporary genetic algorithms. Further, the

inherent concurrency of our FPGA implementation facilitates the integration and testing of micro-populations.

1 INTRODUCTION

Frequently the population-based incremental learning

(PBIL) algorithm is deﬁned as a method that com-

bines both the genetic algorithms paradigm and com-

petitive learning for function optimization. It was de-

vised in the ends of the nineties by S. Baluja as a

way to circumvent the lack of performance of con-

ventional genetic algorithms in some particular opti-

mization problems (Baluja, 1994).

Unlike genetic algorithms, PBIL does not han-

dle an entire population of potential problem solu-

tions. Rather, it only manipulates a single point

around which all the next population elements will

be sampled from. This concept was borrowed from

the competitive learning paradigm (Rumelhart and

Zipser, 1986; Duda et al., 2001; Budura et al., 2006)

leading to the introduction of a probability vector.

During each running epoch, the probability vec-

tor is disturbed toward the best current solution with a

strength that depends on the value of a parameter de-

noted by learning rate. In (Folly and Venayagamoor-

thy, 2009) the effect of the learning rate on PBIL per-

formance was evaluated within a power system con-

troller design framework. The authors describe that,

for high learning rate values, the population diversity

is lost. On the other hand, for low learning rate values,

the algorithm exploration ability is enhanced leading

to a more diversiﬁed population.

The PBIL algorithm was initially devised to work

with a base-2 solution encoding scheme. However,

this is not an absolute condition. Multiple base ver-

sions of PBIL have already been devised by (Servais

et al., 1997). This approach can lead to an increase

solution resolution without incrementing the encod-

ing dimension.

Meta-heuristics algorithms have been applied to

dynamic optimization problems (Yang et al., 2007;

Nguyen et al., 2012). The key issue in dealing with

this type of problems is the ability to maintain the

population adaptability. In (Yang and Yao, 2003) a

dual population PBIL algorithm was devised. This

approach operates on two dual probability vectors re-

garding the search space central point, in order to

maintain the optimum traceability.

One of the main problems in meta-heuristics

search algorithms concerns the duality between ex-

ploration and exploitation. Given a sufﬁcient number

of generations, the typical population becomes biased

toward the best search space point (Gonzalez et al.,

2001); the algorithm is restricted to searching a nar-

row region of the space. Even if other strategies are

Coelho, J., Pinho, T. and Boaventura-Cunha, J..

FPGA Implementation of a Multi-Population PBIL Algorithm.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 279-286

ISBN: 978-989-758-157-1

279

available, one of the promising techniques requires

the parallel evolution, on the same search space, of

two or more PBIL algorithms. For example (Folly,

2013) provides some results regarding the use of dual

population PBIL for power system controller design.

Each population evolves independently. However, the

number of solutions sampled from each probability

vector is variable and depends on the relative ﬁtness

of the best solution found by each population.

The exact nature of this approach claims to be im-

plemented in a dedicated digital processor. In partic-

ular within an architecture that allows the execution

of true parallel processes as in multi-core processors.

Since, in practice, time is a severe handicap associated

to all the evolutionary algorithms, the digital proces-

sor should exchange computation versatility by com-

putation efﬁciency and scalability. For this reason, a

custom designed processor, based for example on a

ﬁeld programmable gate array (FPGA) architecture,

is the obvious choice. On one hand it takes advan-

tage of its combinatory power for fast execution and,

on the other hand, it provides the ability to simultane-

ously run an arbitrary number of PBIL instances.

Hardware implementation of evolutionary algo-

rithms, based on the genetic algorithm paradigm, has

already been performed by several authors. Begin-

ning with the work of (Scott et al., 1995) in the middle

of the nineties, where a general purpose genetic algo-

rithm was implemented using a decentralized topol-

ogy. They reported an average time saving, during

the search procedure, of 94% when compared with

its software implementation. Since the publication of

this seminal work, many others have followed. For

example (Tommiska and Vuori, 1996), (Tang and Yip,

2004), (Fernando et al., 2010) and (Spina, 2010) just

to name a few. However, as far as the authors have

knowledge, the hardware implementation of PBIL has

never been attempted. Some hardware implementa-

tion advantages of PBIL over genetic algorithms can

be enumerated. Namely the fact that PBIL leads to a

lower computation overhead since it is conceptually

simpler and, due to the fact that only the best element

of the population is used, the required memory re-

sources are more parsimony leading to the possibility

of evolving many more populations simultaneously.

In this line of thoughts, this work presents the re-

sults concerning a hardware implementation of both

single population and multi-population PBIL. This

approach will be compared to an equivalent software

implementation using a high level programming lan-

guage having the checkerboard problem as a bench-

mark (Garibay et al., 2003).

The remainder of this work is organized as fol-

lows. Section 2 describes the PBIL algorithm, its

features and how it can be extended to encompass

a multi-population framework. Section 3 deals with

some issues regarding its hardware implementation.

The testbench problem is provided in section 4 to-

gether with the obtained experimental results. Finally,

the main conclusions, and future research directions,

are presented in section 5.

2 THE PBIL ALGORITHM

The population-based incremental learning is a prob-

abilistic search technique which combines notions of

both evolutionary simulation and competitive learn-

ing (Baluja, 1994). Conceptually it belongs to a

class of stochastic search methods generally referred

as “estimation of distribution” algorithms (Larranaga

and Lozano, 2002; Pelikan et al., 2002; Hauschild and

Pelikan, 2011). Transversal to this class of methods is

the concept of probabilistic modelling of solutions. In

PBIL this approach is carried out by means of a data

structure denoted by probability vector. The probabil-

ity vector is expressed as a real-valued vector whose

elements are in the range between 0.0 and 1.0. The

probability vector plays a central role in the opera-

tion dynamics of PBIL. As a matter of fact, and unlike

many evolutionary algorithms, there is no manipula-

tion of individuals using operators such as crossover.

There is no individuals update from one generation to

another. All the operations are done in the probabil-

ity vector entity. Hence one can argue that the PBIL

conceptual approach leads to a simpler algorithm to

implement, when comparing to other meta-heuristic

search methods. This fact translates to a more parsi-

mony use of computational resources such as memory

and algebraic operations.

On its canonical form, the PBIL algorithm con-

sists on two primitives: update and adjustment of the

probability vector. The update primitive is responsi-

ble for the learning step and the adjustment primitive

to keep the exploration ability of the algorithm.

The probability vector update law represents a

disturbance on the actual probability vector toward

the binary pattern of the best current solution. Let

∈ [0, 1]

n×d

denote the probability vector at the cur-

rent generation i. The probability vector, which will

be used to generate the next set of population ele-

ments, is computed by:

i+1

= (1 −ρ) ·ν



1 −(β

⊕ω

)



+ ···

+(ρ + µ) ·(β

∧

) + ρ ·(β

∧ω

)

(1)

where ρ ∈ [0, 1] denotes the learning rate, β

∈

{0, 1}

n×d

is the best found solution at generation i

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

280

and ω

∈{0, 1}

n×d

is the worst solution found at gen-

eration i. The bar over ω denotes the bitwise binary

complement, ⊕ and ∧ the “exclusive or” and “and”

logical operators respectively, 1 is a vector of ones

with dimension n ×d and µ ∈ [0, 1] is usually referred

to as the negative learning rate. This negative learning

rate is an additional disturbance applied to the prob-

ability vector in the direction where the bits from the

best individual differ from the ones of the worst. No-

tice that the dot operation between two equal length

vectors refers to the Hadamard product.

The learning rate parameter has a huge effect on

how PBIL navigates along the search space. In gen-

eral, this coefﬁcient inﬂuences the speed with which

the probability vector tends to the point that is cur-

rently being evaluated. Since in PBIL the probabil-

ity vector is used to generate the next set of sample

points, the learning rate affects the portions of the

function space that will be explored. If the learning

rate is too low, then the algorithm requires a large

number of generations until its behavior deviates from

random walk and becomes following a coherent di-

rection. On the other hand, if the learning rate is too

high then the initial population best individual will

severely bias the rest of the search process toward the

space region around it. This effect of early dominance

prevents a proper search space exploration. This bias-

variance trade-off can be dealt by means of an adap-

tive learning rate. A common choice is to select a

very low learning rate at the beginning of the search

process and then increasing it linearly toward some

maximum value (Folly and Venayagamoorthy, 2009).

The PBIL algorithm also faces the problem of

premature convergence. As the probabilities become

closer to their bounds, the lack of diversity becomes

gradually more pronounced. One way to prevent

this occurrence comprises the deﬁnition of a proba-

bility vector adjustment operation. This operation is

equivalent to the genetic algorithms mutation opera-

tor. However, unlike genetic algorithms, it is usually

applied on the probability vector and not in the indi-

viduals. In PBIL this mutation, or adjustment oper-

ation, takes the appearance of a disturbance on each

probability vector element.

Let ζ

be a vector with dimension n ×d, in GF(2),

and whose j

element is 1 if, and only if, an uniform

generated random number between [0, 1] is lower than

a threshold value, η ∈ [0, 1], designated by mutation

probability. In this context, the probability vector ad-

justment operation is governed according to:

i+1

= (1 −δ ·ζ

) ·ν

+ δ ·ζ

·ε

(2)

where the parameter δ ∈ [0, 1] denotes the mutation

level strength and ε

∈ {0, 1}

n×d

is a binary string

whose elements are drawn, in each generation, from

an uniform two bits random number generator. Once

again 1 ∈ {1}

n×d

As usual there are no exact rules to deﬁne the best

parameters. However, as a rule of thumb, it is fre-

quent to select a learning ratio close to ρ = 0.1 and a

negative learning ratio around µ = 0.07. The mutation

level is usually selected near δ = 0.05. Nevertheless

those values can be made adaptive and change accord-

ing to some set of rules like population variance, gen-

eration progress, among others.

Before ending this section it is important to em-

phasize that, in normal operation, the iterative dis-

tilling of newer solutions leads to a reduction in

the search engine exploration capability. This lack

of diversity can be tackled by increasing the muta-

tion probability η. However, this strategy has al-

ways the side effect of corrupting the knowledge gath-

ered by the PBIL algorithm. In order to bypass this

exploration-exploitation compromise a multiple pop-

ulations strategy can be addressed. The following sec-

tion presents the concept behind this type of solution

and highlights its beneﬁts when compared to the sin-

gle population PBIL.

2.1 Multi-Population PBIL

Parallelization is a frequent word when talking about

population based search methods. This notion usually

refers to the fact that, conceptually, this class of algo-

rithms evaluates a set of solutions in parallel. As a

matter of fact, in the common implementation form,

those solutions are evaluated sequentially within one

generation time window. Nevertheless, this approach

leads to a parallel search engine in contrast to the

usual gradient-based techniques where only an initial

point moves, according to some law, along the search

space local gradient.

On the other hand parallelization can be under-

stood in a multi-population paradigm where a num-

ber of arbitrary distinct populations evolves simulta-

neously. This strategy has been proved to be useful

when dealing with time-dependent optimization prob-

lems (Branke et al., 2000) or as a way to ensure diver-

sity in multi-modal search spaces (Siarry et al., 2002).

Using multiple populations, instead of a single

one, presents many challenges. Specially regarding

the way the information provided by the set of popu-

lations is combined. This issue is transversal to all the

multi-population platforms including PBIL. The only

thing that changes is the complexity on how those in-

terprocess communications occur.

For example in (Yang and Yao, 2003) and (Folly,

2013) two different PBIL populations are generated

over a dynamic search space. Each PBIL instance

FPGA Implementation of a Multi-Population PBIL Algorithm

281

has its own probability vector and the search direc-

tion is biased according to the overall relative best so-

lution. This is accomplished by providing more sam-

pling from the best of the two PBIL instances. If one

probability vector outperforms the other, its sample

size is increased by some arbitrary amount ∆ while

the other is reduced by the same quantity.

In this article an alternative strategy is proposed.

Each PBIL instance will be described within a process

and the inter-processes information sharing is deﬁned

by means of the following law:

= (1 −γ) ·ν

+ γ ·ν

∗

(3)

where the index j ∈ {1, ··· , p} refers to one of the

p populations available from the pool and ν

∗

is the

current best population probability vector. The coef-

ﬁcient γ ∈ [0, 1] is used to deﬁne the amount of cross-

population information sharing. If γ = 0, each popu-

lation independently evolves. Alternatively, if γ = 1,

this paradigm collapses into a single population PBIL.

Further information regarding this technique will

be provided during section 4. The next section deals

with details regarding the hardware implementation

of both single population and multi-population PBIL.

3 HARDWARE DEVELOPMENT

This section presents the implementation details con-

cerning the integration of the algorithm described in

the previous section into a programmable logic de-

vice. This description will be divided into two sub-

sections. The ﬁrst deals with the hardware structure.

In particular the FPGA development board character-

istics and remaining interface hardware. The second

subsection describes the overall algorithm architec-

ture that will be programmed into the FPGA.

3.1 FPGA Development Board

The multi-population PBIL algorithm, discussed in

the previous section, will be embedded into a cus-

tom hardware processor where several population in-

stances can run in real parallel. The digital hardware

processor devised was built over a FPGA manufac-

tured by ALTERA



Corporation. In particular we will

deal with a Cyclone II (EP2C5T144C8) chip which

has a core voltage of 1.2V, 4608 logic elements, 89

user input/output lines (I/O), 117 KB memory and 26

embedded 9 bits hardware (Altera, 2008). For an ex-

haustive information regarding this device character-

istics please refer to the device datasheet or to the sev-

eral booklets provided by ALTERA



on its web site.

The development board used in this work, the

EP2C5/EP2C8, is a very low cost solution that in-

cludes, besides the FPGA itself, a 50 MHz crystal os-

cillator, a pair of voltage regulators and a 4 MB FPGA

conﬁguration memory (EPCS4SI8). The used hard-

ware is illustrated in Figure 1. The left image presents

the overall shape of the development board used and,

the right image, a full preview of the installed hard-

ware. Additionally a 20 ×4 lines LCD display was

interfaced in order to make easily observable the ﬁnal

simulation parameters such as the elapsed time, the

best found solutions and so on.

Figure 1: At the left, an image of the low-cost FPGA devel-

opment board used in this work and, at the right, the exper-

imental setup assembled that includes, besides the develop-

ment board, a 20 ×4 lines LCD display.

The FPGA is set, through a JTAG interface hard-

ware programmer, using the Quartus II software pro-

vided by ALTERA



. This software package follows

an integrated development environment paradigm

where the user accesses to a myriad of different tools

from the same infrastructure. Distinct tools and lan-

guages can be used to describe the target hardware

functionality. Furthermore it is possible to access,

from the same software environment, a set of func-

tions that expands from hardware analysis, synthesis,

program compilation, device programming and dif-

ferent types of simulation capabilities. VHDL is one

of the hardware description languages that the soft-

ware can handle and is the one used during this work.

3.2 FPGA Multi-Population PBIL

In any evolutionary algorithm, independently of its in-

spiration, a number of potential solutions are evalu-

ated, in parallel, during each generation. The search

through the search space ﬂows from those points to-

ward new ones according to some set of rules. The

difference between those rules is what make all the

evolutionary algorithms ﬂavours that exist. From

genetic algorithms, early in the seventies, to krill-

herd optimization passing from ant colonies, cuckoo

search, ﬁreﬂies, glowworms, bats, and so forth. In

this context, parallelism does not refer to the ability

to parallelize the evolutionary algorithm implementa-

tion. It concerns the fact that it is possible to evalu-

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

282

ate an arbitrary number of potential solutions in each

generation. This is usually known as implicit paral-

lelism. Of course this parallelism idea is, in fact, im-

plemented sequentially in the major part of the com-

puter languages. Additionally this type of parallelism

tends to collapse since, after a sufﬁcient number of

generations, the selection pressure bias the solutions

to became the same. Hence, in fact, when the popula-

tion converges the algorithm has the task to evaluate

a large number of very similar solutions. This lack

of population diversity can be tackled by means of

several strategies. For example using mutation oper-

ators or by means of ﬁtness sharing techniques. An-

other more interesting technique is multi-population

evolution where several populations evolve simulta-

neously. This paradigm can be easily implemented

using programmable logic devices since, within this

type of hardware, it is possible to effectively evolve,

in true concurrent conﬁguration, a set of smaller size

populations. Those populations share information be-

tween them by an intelligence exchange mechanism

in order to simultaneously explore the full extend of

the search space while maintaining inter-population

diversity. This kind of concurrent evolution of several

populations is usually referred as explicit parallelism.

In the case of genetic algorithms, there have been

already many attempts to implement this method into

a FPGA. However, they usually involve only a sin-

gle population with the aim of take advantage of

the fast processing power provided by combinatorial

processors (Scott et al., 1995; Tommiska and Vuori,

1996; Tang and Yip, 2004; Narayanan, 2005; Fer-

nando et al., 2010; Spina, 2010). In this work an

alternative evolutionary structure is embedded into a

FPGA. However, as far as the present authors have

knowledge, there was never been any attempt to im-

plement the PBIL in hardware. This believe is even

stronger given that our aim is to put forward an ar-

chitecture that is able to handle several populations in

parallel. In this context Figure 2 presents the overall

multi-population PBIL algorithm structure embedded

within the FPGA.

Figure 2: FPGA multi-population PBIL architecture.

As shown in the ﬁgure above, each PBIL instance

is executed inside a process and, in abstract, it is pos-

sible to set p populations simultaneously. Each pop-

ulation has its own probability vector and, after ﬁt-

ness evaluation, its values are updated. The update is

performed taking into consideration each population

current best individual and the inter-population best

individual. The objective of the inter-process com-

munication module is to provide, at any time instant,

the best global individual to each of the running PBIL

instances. At each processing cycle, all the processes

are executed and, inside each process, a n population

PBIL instance is embedded.

Inside the process the single population PBIL op-

erations sequence is performed: ﬁrst the N population

elements are generated according to the present prob-

ability vector. Then each element ﬁtness is computed

and both the best and worst elements are used in the

probability vector update scheme. The probability ac-

tualization also requires the knowledge of the current

best inter-population individual. This information is

provided by the inter-process communication module

which is, in its essence, just a shared variable.

A fundamental module, virtually in all evolution-

ary algorithms, is the random number generator. This

block also plays a fundamental role in the PBIL al-

gorithm activity. As a matter of fact its activity range

from population generation to the mutation operation.

Even if true randomness is impossible to achieve

using deterministic software rules, it is possible to

generate number sequences with a very low autocor-

relation index for lags higher than zero. There are sev-

eral methods to obtain those kind of sequences. Some

of the most popular ones are the linear feedback shift

linear congruential generator (LCG). Nevertheless it

seems that the choice of the random number genera-

tor method is not critical to the evolutionary algorithm

performance (Meysenburg and Foster, 1999; Martin,

2002). In this work a LCG random number generator

strategy with a 31 bit modulus and a multiplier equal

to 2147483629 was used.

Having described the multi-population PBIL

hardware architecture, the following section will deal

with its use in ﬁnding a solution of a classical opti-

mization problem commonly known as the checker-

board challenge.

4 EXPERIMENTAL RESULTS

The problem addressed in this article regards the

checkerboard problem referred in (Baluja, 1994). The

objective is to be able to ﬁnd a solution that will

FPGA Implementation of a Multi-Population PBIL Algorithm

283

closely match the pattern of a generic checkerboard.

A checkerboard is a matricial square structure, with a

total of d elements, with two types of cells, “black”

and “white”, arranged in an alternated colour pattern

along its lines or columns.

Let the checkerboard colour cells be encoded by

an one bit variable. For example “black” is associ-

ated to logical “1” and “white” to logical “0”. Each

location with a ‘1’ should be surrounded, in all four

directions, by a ‘0’ and vice-versa with the exceptions

of the cells located at the board boundaries. Follow-

ing this reasoning, the problem solution will be en-

coded as a d bit string. In particular, in this work, a

576 bit solution string will be assumed. This solution

can be interpreted as a particular pattern for a 24×24

checkerboard grid.

In short, the PBIL algorithm will be tested regard-

ing its ability to generate a solution that matches the

checkerboard pattern of ‘0’ and ‘1’ with the highest

probability possible. To perform this operation an ob-

jective function must be devised that will be used to

assign a degree of performance to a given solution. In

(Baluja, 1994) this ﬁtness is measured by counting the

number of correct surrounding bits, of each bit posi-

tion, for a subspace grid centred at the space checker-

board. That is, the squares lines that follow the board

boundary are not taken into account on the objective

function. In this work all the table cells are consid-

ered. In particular the objective function regards the

product of the number of different bits between a par-

ticular solution and two different template vectors that

match the two possible board distribution layouts. In

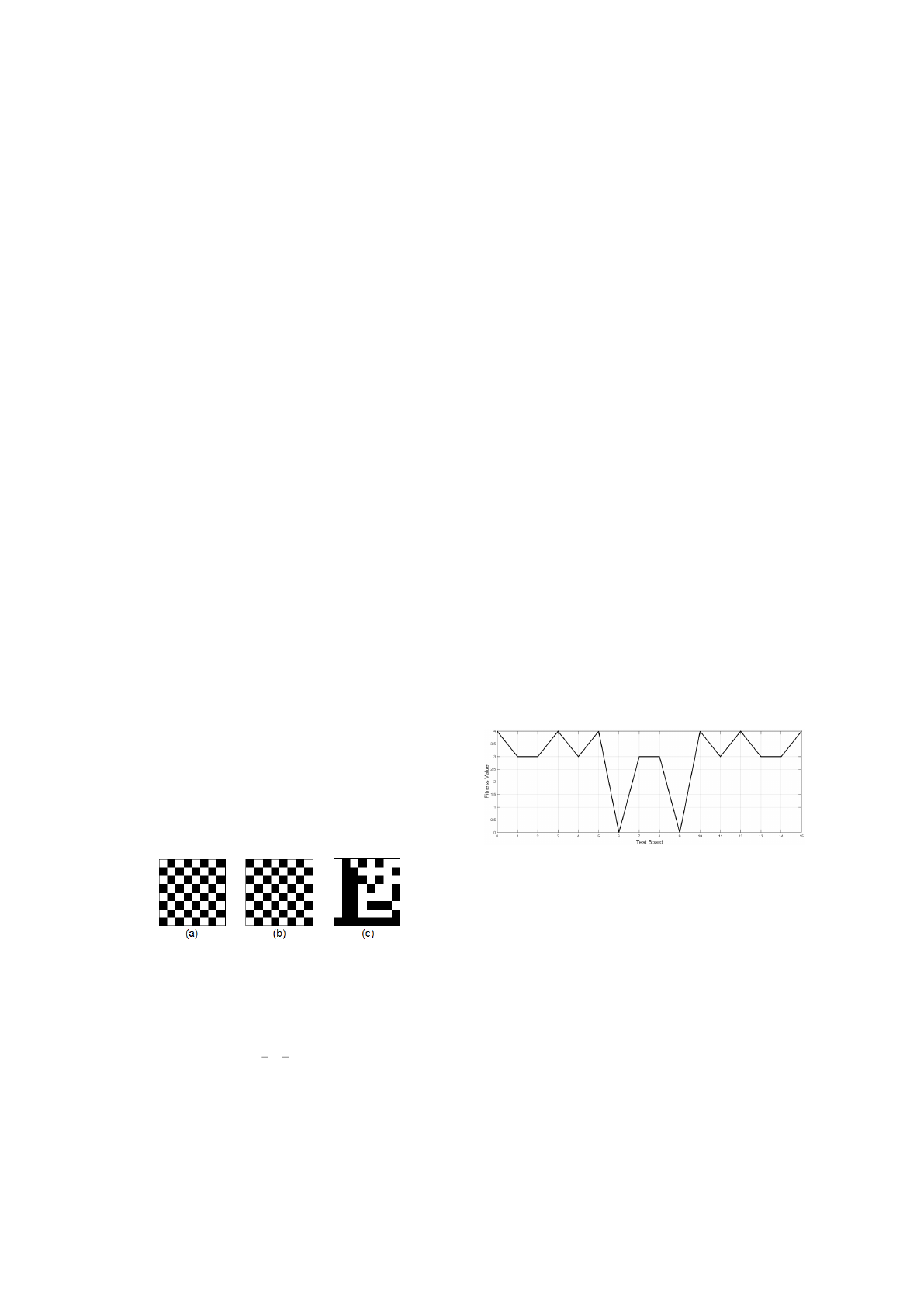
order to illustrate this concept refer to Figure 3 where

(a) and (b) represent the two valid board conﬁgura-

tions for a 8 ×8 cells checkerboard. As it can be eas-

ily seen, one of the boards is just a 90 degree rotation

of the other. Recall that the state of each board cell is

coded using one bit information. In particular a black

cell is represented as ‘1’ and a white cell as ‘0’.

Figure 3: (a) and (b) regard the two possible checkerboard

templates. (c) is an example of an arbitrary generated board.

The image presented in Figure 3 (c) refers to an

arbitrary generated board. Its matching degree, re-

garding one of the template boards, is computed by:

√

∑

i=1

√

∑

j=1

i j

⊗b

i j

(4)

where t ∈ {a, b} refers to one of the two possible

board templates: the one from Figure 3 (a) or Figure

3 (b). The variable d is the board dimension, i.e., the

total number of board cells, and t

i j

is the logical value

regarding the cell located at i

row and j

column

on the template board t. In the same line of taught,

i j

refers to the logical value of a cell placed at line i,

column j, of the an arbitrary board b.

For the example illustrated in Figure 3 the value of

is equal to 39 and F

equal to 25. Those numbers

can be interpreted as the closeness between the arbi-

trary generated board and the two possible target pat-

terns. The objective function that the algorithm will

seek to optimize is the product of F

by F

. This will

lead to a ﬁtness value for the board in Figure 3 (c)

equal to 975. Hence the problem can be putted as to

ﬁnd an arbitrary board b which minimizes the objec-

tive function:

F =

∏

(5)

Notice that no constraints regarding the equilib-

rium between the number of white and black cells

are imposed. Hence the full factorial set of the d bits

strings is considered admissible.

In order to get an intuition about the problem com-

plexity let the board b be interpreted as the d bits bi-

nary encoding of integers between 0 and 2

−1. As

can be viewed, the number of possible boards com-

binations grows exponentially with d. For now let’s

assume a very small board with d = 4. In this frame-

work the objective function expressed at (5) can be

represented, in a 1D plot, by Figure 4.

Figure 4: Fitness value as a function of all the possible 16

cells combinations for a 2 ×2 checkerboard. The abcissas

regards the integer conversion of the binary codeword ob-

tained by taking the bits along the table lines, from left to

right, assuming that the most signiﬁcant bit is at the upper

left corner and the least signiﬁcant the one at the lower right

table corner.

From visual inspection it is possible to observe the

multimodal nature of the problem as long as the ex-

istence of two minima locations. There are no sys-

tematic paths along which the optimization algorithm

could infer the optima location. In this context it is a

complex problem.

Due to the FPGA true parallel processing capabil-

ity, the implementation of the PBIL version, which

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

284

promotes the co-evolution of many populations si-

multaneously, is the current addressed methodology.

The ﬁrst set of experiments will be conducted us-

ing a software approach. The PBIL algorithm, de-

scribed at section 2.1, was codded, within a numeri-

cal computation environment, using a high level com-

puter language. The implemented programs were

fully vectorized for speed purposes and run over an

Intel



Core

I5-3230M processor platform.

A total of 10 PBIL instances, each one evolving

10 population elements, were executed during 2500

generations using ρ = 0.01, µ = 0.0005, η = 0.02

and δ = 0.005. Remark that, instead of initializ-

ing the probability vectors with the constant 0.5, this

data structure was loaded, for each of the 10 popu-

lations, using values taken from a normal distributed

(pseudo) random number process with values in the

range ]0, 1[. With this strategy it is assured that the al-

gorithm explores different points of the search space.

The ﬁrst set of one hundred experiments was con-

ducted assuming γ = 0. Each of the ten populations

average ﬁtness is presented at Figure 5.

Figure 5: Multi-population average ﬁtness evolution, along

2500 generations, using 100 tryouts.

As can be seen, in average, all the popula-

tions have the same behavior regarding its conver-

gence. Moreover, without cross communication be-

tween processes, neither one of the ten populations

was able to converge consistently to one of the two

possible global optima. Regarding the computational

load it was measured an average CPU time, per run,

of 7.8 seconds. After increasing the cross-population

information, by incrementing γ from 0 to 0.1, and

repeating the experiment sets, it is now possible to

observe, from Figure 5, that the convergence to the

global minimum is consistently achieved in contrast

to the previous case. Furthermore, by increasing even

more the value of γ, it is possible to witness a faster

convergence rate. To illustrate this statement, Fig-

ure 5 presents the convergence rate assuming γ = 0.8.

The best solution is now found after less than 2000

generations in contrast with the earlier case where

2500 generations were, in average, needed to ﬁnd

the optima. From the obtained results it is possible

to conclude that the PBIL is able to ﬁnd the solu-

tion of the checkerboard problem as initially stated

in (Baluja, 1994). In this paper it was shown that this

was even possible by dividing a large population into

smaller ones. This large population dismemberment,

into lower size ones, favors its implementation in a

parallel processing environment. Moreover different

initial points on the surface can be explored simul-

taneously by providing different initial probabilities

vectors to each population in the pool. It is also pos-

sible to conﬁrm the success of the inter-population in-

formation exchange strategy devised. Filtering each

of the probability vectors using the one from the best

ﬁttest population promotes a faster convergence to a

global optimum. Having established that this opti-

mization approach is an effective method to solve the

checkerboard problem, the next step is to execute it

on the dedicated hardware digital processor. Under

this condition, the hardware based multi-population

PBIL was driven under the same test conditions as the

software version regarding both the number of popu-

lations, individuals per population and remain tuning

parameters. As expected, in term of convergence, the

obtained results were equivalent to the ones presented

at Figure 5. However, by using dedicated hardware,

the execution time was substantially decreased by a

factor near 3. That is, similar results were obtained,

at the end of 2500 generations, after only 2.8 seconds.

This time reduction can be further decreased by using

an higher performance FPGA’s such as the ones form

the ALTERA



STRATIX family. This can lead to the

possibility of using this type of optimization method

in real-time applications when high dynamics are in-

volved.

5 CONCLUSIONS

The PBIL has, at the present time, more than two

decades of existence. This is a stochastic optimiza-

tion method belonging to a broad class of methods

known under the designation of distribution estima-

tion algorithms. Even if this method has proven to

be very effective on solving some types of problems

where other meta-heuristic approaches fail, it has be-

come gradually obscured by the proliferation of a

countless new evolutionary methods such as particle

swarm optimization, cuckoo search, krill heard opti-

mization among many other methods. However, nei-

ther of them has reached, in the present authors opin-

ion, the degree of simplicity and ﬂuidity of PBIL. As

a matter of fact, the PBIL algorithm is conceptually

simpler which leads to faster execution times when

compared with the other techniques. Processing time

is a very important issue when dealing with problems

requiring large population evolving during extensive

FPGA Implementation of a Multi-Population PBIL Algorithm

285

generations number or when real-time solution ﬁnd-

ing must be provided. Allied to the optimization al-

gorithm simplicity, the execution time can be narrow

down by using a special designed digital processor in-

stead of a general purpose microprocessor such as the

ones that equip the common domestic personal com-

puters. The main contributions of this work can be

summarized into three main points: the demonstra-

tion that it is possible to execute, in a very efﬁcient

fashion, the PBIL algorithm using a programmable

logic device; the fact that, in this case, the exten-

sion of the original single-population approach to a

multi-population one is naturally extended through

the instantiation of new VHDL processes; and ﬁnally

that the interconnection between the populations, in

a multi-population framework, can happen easily at

the probability vectors level. This multi-population

hardware based approach was applied to the checker-

board problem which has been proved to be a decep-

tive type problem for other evolutionary algorithms.

Namely the genetic algorithms. The obtained results

show that, not only the PBIL algorithm was able to

solve the problem, but it was able to do it in a time

fraction when comparing to its implementation using

a pure software approach over a generic microproces-

sor platform.

REFERENCES

Altera (2008). Cyclone ii device handbook (volume i).

Technical report, Altera Corporation.

Baluja, S. (1994). Population-based incremental learning.

Technical report, Carnegie Mellon University.

Branke, J., Kaussler, T., Smidt, C., and Schmeck, H. (2000).

A multi-population approach to dynamic optimization

problems. In Evolutionary Design and Manufacture.

Springer London.

Budura, G., Botoca, C., and Miclau, N. (2006). Compet-

itive learning algorithm for data clustering. Electron

Energetics, 19(2):261–269.

Duda, R., Hart, P., and Stork, D. (2001). Pattern classiﬁca-

tion. John Wiley & Sons.

Fernando, P., Katkoori, S., Keymeulen, D., Zebulum, R.,

and Stoica, A. (2010). Customizable fpga ip core im-

plementation of a general-purpose genetic algorithm

engine. Evolutionary Computation, IEEE Transac-

tions on, 14:133–14.

Folly, K. (2013). Parallel pbil applied to power system con-

troller design. Journal of Artiﬁcial Intelligence and

Soft Computing Research, Vol. 3, No. 3:215–223.

Folly, K. A. and Venayagamoorthy, G. K. (2009). Effect

of learning rate on the performance of the population

based incremental learning algorithm. In Proceed-

ings of International Joint Conference on Neural Net-

works.

Garibay, O., Garibay, I., and Wu, A. (2003). The modular

genetic algorithm: Exploiting regularities in the prob-

lem space. In Computer and Information Sciences -

ISCIS 2003. Springer Berlin Heidelberg.

Gonzalez, C., Lozano, J., and Larranaga, P. (2001). The

convergence behavior of the pbil algorithm: A prelim-

inary approach. In Artiﬁcial Neural Nets and Genetic

Algorithms. Springer Vienna.

Hauschild, M. and Pelikan, M. (2011). An introduction

and survey of estimation of distribution algorithms.

Swarm and Evolutionary Computation, 1:111 – 128.

Larranaga, P. and Lozano, J., editors (2002). Estimation of

distribution algorithms: A new tool for Evolutionary

Computation. Kluwer, Boston.

Martin, P. (2002). An analysis of random number gener-

ators for a hardware implementation of genetic pro-

gramming using ffpga and handel-c. Technical report,

University of Essex.

Meysenburg, M. M. and Foster, J. A. (1999). Random gen-

erator quality and gp performance. In Proceedings of

the Genetic Evolutionary Computation Conference.

Narayanan, S. (2005). Hardware implementation of Genetic

Algorithm modules for intelligent systems. PhD thesis,

University of Cincinnati.

Nguyen, T. T., Yang, S., and Branke, J. (2012). Evolution-

ary dynamic optimization: A survey of the state of the

art. Swarm and Evolutionary Computation, 6:1–24.

Pelikan, M., Goldberg, D., and Lobo, F. (2002). A survey of

optimization by building and using probabilistic mod-

els. Computational Optimization and Applications,

21:5–20.

Rumelhart, D. and Zipser, D. (1986). Feature discovery by

competitive learning. MIT Press.

Scott, S., Samal, A., and Seth, S. (1995). Hga: A hardware-

based genetic algorithm. In Third International ACM

Symposium on Field-Programmable Gate Arrays.

Servais, M., de Jager, G., and Greene, J. R. (1997). Function

optimisation using multiple-base population based in-

cremental learning. In in Proceedings of the Eighth

Annual South African Workshop on Pattern Recogni-

tion.

Siarry, P., P

etrowski, A., and Bessaou, M. (2002). A multi-

population genetic algorithm aimed at multimodal op-

timization. Adv. Eng. Softw., 33:207–213.

Spina, M. L. (2010). Parallel genetic algorithm engine on

a FPGA. PhD thesis, University of South Florida.

Tang, W. and Yip, L. (2004). Hardware implementation of

genetic algorithms using fpga. In Proceedings of the

47th MWCAS.

Tommiska, M. and Vuori, J. (1996). Implementation of ge-

netic algorithms with programmable logic devices. In

Proceedings of 2NWGA.

Yang, S., Jin, Y., and Ong, Y., editors (2007). Evolution-

ary Computation in Dynamic and Uncertain Environ-

ments. Springer-Verlag.

Yang, S. and Yao, X. (2003). Dual population-based incre-

mental learning for problem optimization in dynamic

environments. In 7th Asia Paciﬁc Symposium on In-

telligent and Evolutionary Systems.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

286