Planning Training Loads to Develop Technique and Rhythm in the 400 m
Hurdles using RBF Network
Krzysztof Przednowek
1
, Janusz Iskra
2
, Stanislaw Cieszkowski
1
and Karolina H. Przednowek
1
1
Faculty of Physical Education, University of Rzeszow, Rzeszow, Poland
2
Faculty of Physical Education and Physiotherapy, Opole University of Technology, Opole, Poland
Keywords:
Hurdle Races, Technique In Hurdles, Artificial Neural Networks.
Abstract:
In this paper training loads to develop technique and rhythm in hurdles are presented. The training loads were
generated using an artificial neural networks model with radial basis functions. The analysis included 21 hur-
dlers who were members of the Polish National Team. The calculations for the neural model were made using
48 training programmes. The evaluation of the models was carried out using the cross-validation method.
Five independent variables (age, body height, body weight, current result and expected result) and four de-
pendent variables representing the selected training loads were analyzed. The determined model generated
training loads with an error of approximately 21%. Experimental results showed the training programme for
a hypothetical athlete. The analysis shows that all the examined training loads are of a non-linear nature. The
proposed solution can be used as a tool to support planning for selected training loads in 400 m hurdles.
1 INTRODUCTION
Hurdles races are complex athletic events since they
require both motor and technical skills. The re-
sults achieved in these races depend on the level of
strength, the jumping technique and the so-called hur-
dle rhythm (McFarlane, 2000). In the 400 m hurdles
technique plays an exceptional role. The use of ap-
propriate technical skills while taking off, jumping
over the hurdle and landing, is very important. The
400 m hurdles technique is usually referred to as that
of jumping 10 hurdles, each 91.4 cm high. It includes
the individual stages of the race, i.e. start, racing to
the first hurdle, racing through the hurdles and rac-
ing to the finish line. Hurdling, and strictly speaking
jumping over the hurdle, is a form of complex, dy-
namic motion, described in studies as a classic exam-
ple of using the laws of physics in sport (Iskra, 2012).
The evaluation of race technique comes down
to the biomechanical assessment of each individual
component (
ˇ
Coh et al., 2008). In the course of biome-
chanical analysis, errors in movement are discovered
and can be subsequently corrected by means of an ap-
propriate training plan. While planning the training
loads, the coach very often relies exclusively on his
own expertise. Such an approach sometimes lacks
scientific basis. It is therefore necessary to look for
solutions that would support the planning of train-
ing loads. One such solution may be the application
of advanced mathematical models (Maszczyk et al.,
2014; Wiktorowicz et al., 2015). Using these tech-
niques leads to a better understanding of the subject
under consideration. The most commonly used meth-
ods of mathematical support for the process of sports
training include artificial neural networks (Ryguła,
2005; Pfeiffer and Perl, 2006; Perl et al., 2013; Silva
et al., 2007). In sports science neural models are
widely used for modelling, prediction and optimiza-
tion. These models make it possible to predict sport-
ing talent (Roczniok et al., 2007) or determine the
impact of the training on the result achieved (Przed-
nowek et al., 2014). In this study we therefore, de-
cided to use artificial neural networks in planning the
training loads to develop technique and rhythm.
A novel approach to planning training loads de-
veloped by the authors, is the construction of model-
generated training loads using selected parameters
characterizing the athlete and his current results. This
supports the planned training programme in the train-
ing period under consideration (special preparation
period). The main purpose of this study is the con-
struction of artificial neural networks to generate the
training loads to develop selected technique compo-
nents in a 400 m hurdles race. The construction of the
model was based on training data from athletes with
a high level of fitness.
Przednowek, K., Iskra, J., Cieszkowski, S. and Przednowek, K..
Planning Training Loads to Develop Technique and Rhythm in the 400m Hurdles using RBF Network.
In Proceedings of the 3rd International Congress on Sport Sciences Research and Technology Support (icSPORTS 2015), pages 245-249
ISBN: 978-989-758-159-5
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
245

2 MATERIAL AND METHODS
2.1 Training Data
The training data used for the construction of the
training planning model were taken from athletes
competing at a high level. The analysis included
21 Polish hurdlers who were members of the Polish
National Team and represented Poland at Olympic
Games, and European and World Championships.
The 48 training programmes carried out during the
special preparation period were selected. Addition-
ally the results before and after the analyzed training
period were registered. The special preparation pe-
riod usually lasts about three months (from February
to May). Five independent variables (x
1
– age, x
2
–
body height, x
3
– body weight, x
4
– current result, x
5
– expected result) and four dependent variables (y
1
,
y
2
, y
3
, y
4
) representing the training loads were ana-
lyzed. A training load is the work or exercise that an
athlete performs during a training session. The se-
lected training loads are those loads which make up
technique and rhythm (Tab. 1). The values of these
training loads are measured in a number of races. The
basic statistic ( ¯x – mean value, min – minimum, max
– maximum, sd - standard deviation) of the variables
used to calculate the model are presented in Table 1.
Due to the difficulties connected with carrying
out the test in 400 m hurdles races during the special
preparation period (winter), the athletes ran a 500 m
test race (flat run). As demonstrated in the previous
study, the result of a 500 m race reflect the hurdler’s
current performance in a 400 m race (Alejo, 1993;
Przednowek et al., 2014). In this study, the 500 m flat
run was adopted as an indicator of fitness level.
2.2 The Idea of Supporting the Training
Process
The proposed method to support the training process
involves the use of a mathematical model to gener-
ate training loads with given input parameters (inde-
pendent variables). The coach using the model inputs
age, body weight and body height statistics for the
competitor (Fig. 1). At this stage his current result
for the 500 m race is entered, which reflects his cur-
rent physical condition and the result expected. At the
output stage of the model the values of the training
loads are generated (Fig. 1). The loads thus gener-
ated constitute a training plan to prepare the hurdler
for the special preparation period. The values appear-
ing at outputs y
1
–y
4
represent the sum of all loads of
that type, which should be implemented during the
entire training period. Based on the suggestions from
Generating
of training
loads
x
1
x
2
x
3
x
4
x
5
y
1
y
2
y
3
y
4
1
Figure 1: Block diagram of models generating training
loads.
the system, the coach plans the training loads to be
carried out each day during the special preparation pe-
riod.
2.3 Calculating and Evaluating Method
In the conducted analysis, the model of an artificial
neural network with radial basis functions (RBF) was
applied (Bishop, 2006). Networks with a radial ba-
sis functions have one hidden layer, composed of ra-
dial neurons and an output layer consisting of linear
neurons. The RBF networks were implemented us-
ing the Statistica 10 software (StatSoft, Inc., 2011).
In the process of finding the best model, networks
with various numbers of neurons in the hidden layer
(from 0 to 10) were analyzed. During the evalua-
tion of the neural network, the leave-one-out cross-
validation method was used (James et al., 2013);
cross-validation error was defined as:
CV
j
=
q
1
n
∑
n
i=1
(y
i j
− ˆy
−i j
)
2
max(y
j
) − min(y
j
)
· 100, (1)
where: n – number of patterns (48), y
i j
– real value,
ˆy
−i j
– the output value constructed in i–th step of
cross-validation based on a data set containing no test-
ing pair (x
i
,y
i
), CV
j
– cross validation error for j–th
output. The main criterion for model selection was
the arithmetic error average, calculated for all net-
work outputs. The cross-validation was implemented
using Visual Basic language.
3 RESULTS
The research results are demonstrated in two sections.
In the first one, the model calculation is presented,
while in the second section the generated training
loads are analyzed.
icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support
246

Table 1: Description of the variables.
Variable Description ¯x min max sd
x
1
Expected results on 500 m run (s) 65.06 61.50 69.10 1.80
x
2
Age (years) 22.25 19.00 27.00 1.97
x
3
Body height (cm) 185.04 177.00 192.00 4.70
x
4
Body weight (kg) 74.29 69.00 82.00 2.71
x
5
Current results on 500 m run (s) 66.78 62.50 71.15 1.68
y
1
Runs over 1–3 hurdles (amount) 46.40 3.00 148.00 28.87
y
2
Runs over 4–7 hurdles(amount) 82.38 4.00 176.00 40.23
y
3
Runs over 8–12 hurdles (amount) 79.71 0.00 194.00 45.83
y
4
Hurdle runs in varied rhythm (amount) 330.02 0.00 745.00 156.35
2 4 6 8 10
21.5 22.0 22.5 23.0 23.5
Number of neurons in hidden layer
¯
CV
j
Figure 2: Mean cross-validation errors; The X-axis repre-
sents the number of neurons in the hidden layer of RBF
network which range from 1 to 10. The Y-axis represents
the mean value of CV
j
error for all outputs.
y
1
y
2
y
3
y
4
CV
j
0 5 10 15 20
20.14
22.61
21.58
21.16
Figure 3: Cross-validation errors CV
j
of each output.
3.1 Model Calculation
In order to determine the network featuring the best
generalization ability, a cross-validation was per-
formed. Networks with hidden neurons from 1 to 10
were examined. The cross-validation results are pre-
sented in Figure 2.
The conducted analysis shows that the best model
is the artificial neural network with seven neurons in
the hidden layer. That network generates an average
cross-validation error of 21%. Errors generated by in-
dividual network outputs are presented in Figure 3.
Output y
1
is characterized by the smallest generaliza-
tion error (20.14%), while the y
2
output features the
largest error (22.61%).
3.2 Generation of Training Loads
The next step in the analysis was to calculate the train-
ing loads using the selected RBF network. On the
network input, the data from a hypothetical athlete
(age 21, body height 185 cm, weight 75 kg) were en-
tered. Loads were generated on the assumption that
the 500 m race results would be improved by one sec-
ond, taking as the output result, results from 68 s to
62 s, respectively. The range of result from 68 s to
62 s reflects the career of a hurdler. The results of
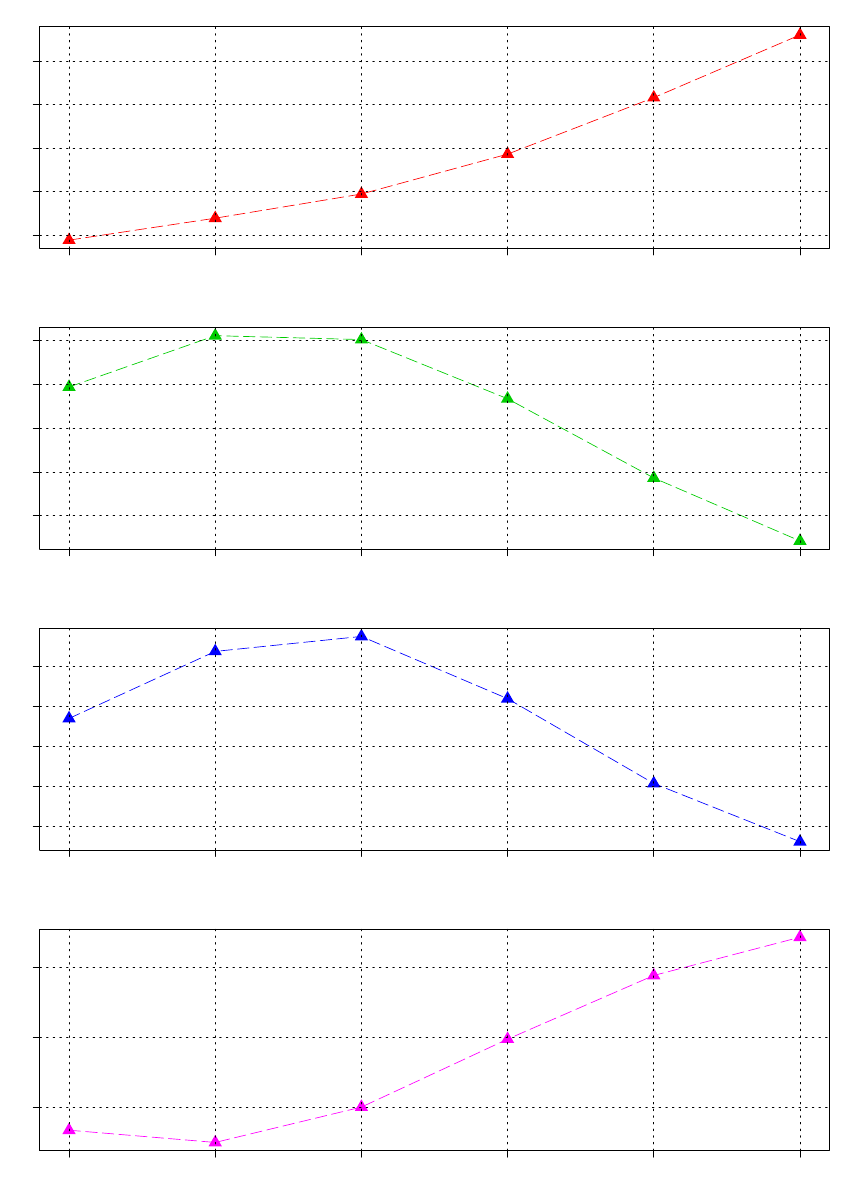
this experiment are presented in Figure 4. The graphs
show loads generated in such a way that the Y-axis
represents the level of training loads while the X-axis
is the expected result. The values on the X-axis are
placed in descending order as the increase in the com-
petitors’ sports level is associated with a decrease in
the time they achieve over a specified distance. For
example, if a competitor wants to improve his result
from 66 s to 65 s then the generated training plan indi-
cates that the competitor should implement a workout
with the following capacity: y
1
= 54; y
2
= 91; y
3
= 87
and y
4
= 225.
The analysis of training loads generated for hypo-
thetical athletes shows that all the examined loads are
of non-linear nature (Fig. 4). Considering the values
calculated for y
1
(Fig. 4(a)), it should be noted that as
well as the achievement of better results, the volume
of the loads increases. The maximum value of y
1
is
observed when the athlete demonstrates a high level
of fitness.
A different trend is observed for the values gener-
ated at the y
2
output (Fig. 4(b)). Initially, there is a
slight increase of the value and stabilization at sports
level of 65–64 seconds. In the later stages of a ca-
reer it can be seen that as the athlete’s sports level
increases, the y
2
value decreases.
Planning Training Loads to Develop Technique and Rhythm in the 400m Hurdles using RBF Network
247
66 65 64 63 62 61
50 60 70 80 90
Result on 500 m [s]
y
1
[amount]
a)
66 65 64 63 62 61
70 75 80 85 90
Result on 500 m [s]
y
2
[amount]
b)
66 65 64 63 62 61
65 70 75 80 85
Result on 500 m [s]
y
3
[amount]
c)
66 65 64 63 62 61
250 300 350
Result on 500 m [s]
y
4
[amount]
d)
Figure 4: Training loads generated by the RBF network for a hypothetical athlete (age 21, body height 185 cm, weight 75 kg);
The X-axis represents the expected results ranging from 68 s to 62 s. The Y-axis represents the value of training loads.
icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support
248
The third set of generated training load are runs
over 8–12 hurdles (y
3
). As can be seen from the pre-
sented graph (Fig. 4(c)) the value of these load in-
creases until the athlete achieves a 64 s result. Sub-
sequently, as the sports level increases so the size of
this load decreases. A similar situation was observed
for y
2
.
The final set of training loads analyzed are hurdle
runs in varied rhythms (y
4
). The values of these loads
change in non-linear fashion during the whole period
being considered (Fig. 4(d)). In the early stages a
career the value of these loads is low. It is significant
that when the outcome is equal to 65 s the value of y
4
grows steadily, assuming its maximum value when an
athlete has reached the highest level of fitness.
4 CONCLUSIONS
In this paper the model for generated training loads
to develop techniques was calculated. The model was
calculated using artificial neural networks with radial
basis functions. The best RBF network has seven neu-
ron in the hidden layer and generates errors at the
level of 21%.
The generated training loads change non-linearly
over the whole of an athlete’s career; the training
loads y
3
(runs over 8–12 hurdles) can serve here as
an example. Their value increases systematically up
to the moment when the athlete achieves an interme-
diate level (approx. 64 s in a 500 m flat run), and af-
ter that it decreases to the end of the athlete’s career.
The analysis also shows that at a high sports level the
size of y
1
and y
4
should be increased (a run over 1–3
and 8–12 hurdles) and the size of y
2
and y
3
should be
decreased (runs over 4–7 hurdles and hurdles runs in
varied rhythm).
The implementation of artificial neural networks
with radial basis functions in training loads analysis
can support the hurdles training process. The results
obtained can be regarded as suggestions to be used
while planning these loads.
REFERENCES
Alejo, B. (1993). Weight training for the 400-m hurdler.
Track Technique, (123):3915–3918.
Bishop, C. M. (2006). Pattern Recognition and Ma-
chine Learning. Information Science and Statistics.
Springer-Verlag New York, Inc., Secaucus, NJ, USA.
ˇ
Coh, M., Dolenec, A., Toma
ˇ
zin, K., and Zvan, M. (2008).
Dynamic and kinematic analysis of the hurdle clear-
ance technique. In
ˇ
Coh, M., editor, Biomechanical
Diagnostic Methods in Athletic Training, pages 109–
116. University of Ljubljana.
Iskra, J. (2012). Scientific research in hurdle races. AWF
Katowice.
James, G., Witten, D., Hastie, T., and Tibshirani, R. (2013).
An introduction to statistical learning. Springer.
Maszczyk, A., Golas, A., Pietraszewski, P., Roczniok, R.,
Zajac, A., and Stanula, A. (2014). Application of neu-
ral and regression models in sports results prediction.
Procedia-Social and Behavioral Sciences, 117:482–
487.
McFarlane, B. (2000). The Science of Hurdling and Speed.
Athletics Canada.
Perl, J., Grunz, A., and Memmert, D. (2013). Tactics anal-
ysis in soccer–an advanced approach. International
Journal of Computer Science in Sport, 12(2013):33–
44.
Pfeiffer, M. and Perl, J. (2006). Analysis of tactical struc-
tures in team handball by means of artificial neural
networks. International Journal of Computer Science
in Sport, 5(1):4–14.
Przednowek, K., Iskra, J., and Przednowek, K. H. (2014).
Predictive modeling in 400-metres hurdles races. In
2nd Int. Congress on Sport Sciences Research and
Technology Support - icSPORTS 2014, pages 137–
144. SCITEPRESS, Rome, Italy.
Roczniok, R., Ryguła, I., and Kwa
´
sniewska, A. (2007). The
use of Kohonen’s neural networks in the recruitment
process for sport swimming. Journal of Human Kinet-
ics, 17:75–88.
Ryguła, I. (2005). Artificial neural networks as a tool
of modeling of training loads. In Engineering in
Medicine and Biology Society, 2005. IEEE-EMBS
2005. 27th Annual International Conference of the,
pages 2985–2988.
Silva, A. J., Costa, A. M., Oliveira, P. M., Reis, V. M.,
Saavedra, J., Perl, J., Rouboa, A., and Marinho, D. A.
(2007). The use of neural network technology to
model swimming performance. Journal of Sports Sci-
ence and Medicine, 6(1):117–125.
StatSoft, Inc. (2011). STATISTICA (data analysis software
system), version 10. www.statsoft.com.
Wiktorowicz, K., Przednowek, K., Lassota, L., and Krzes-
zowski, T. (2015). Predictive modeling in race walk-
ing. Computational Intelligence and Neuroscience.
Planning Training Loads to Develop Technique and Rhythm in the 400m Hurdles using RBF Network
249
