Evolutionary Nonlinear Model Output Statistics for Wind Speed

Prediction using Genetic Programming

Kisung Seo and Byeongyong Hyeon

Department Electronic Engineering, Seokyeong University, Jungneung-Dong 16-1, Sungbuk-Gu, Seoul, South Korea

Keywords: Wind Speed Prediction, Nonlinear MOS, Genetic Programming.

Abstract: Wind speed fluctuates heavily and affects a smaller locality than other weather elements. Wind speed is

heavily fluctuated and quite local than other weather elements. It is difficult to improve the accuracy of

prediction only in a numerical prediction model. An MOS (Model Output Statistics) technique is used to

correct the systematic errors of the model using a statistical data analysis. Most previous MOS (Model

Output Statistics) used a linear regression model, but they are hard to solve nonlinear natures of the weather

prediction. In order to solve the problem of a linear MOS, a nonlinear compensation technique based on

evolutionary computation is introduced as a new attempt. We suggest a nonlinear regression method using

GP (Genetic Programming) based symbolic regression to generate an open-ended nonlinear MOS. The new

nonlinear MOS can express not only nonlinearity much more extensively by involving all mathematical

functions, including transcendental functions, but also unlimited orders with a dynamic selection of

predictors due to the flexible tree structure of GP. We evaluate the accuracy of the estimation by GP based

nonlinear MOS for the three days wind speed prediction for Korean regions. The training period of 2007-

2009, 2011 year is used, the data of 2012 year is for verification, and 2013 year is adopted for test. This

method is then compared to the linear MOS and shows superior results.

1 INTRODUCTION

Due to the development of information technology,

the collection of a huge weather data becomes

easier. The installation of AWS (Automatic Weather

Station) is increasing continuously, which can

observe data

of weather elements such as

temperature, precipitation, and wind speed

automatically via sensors and computers. Thus the

importance of numerical prediction weather models

using long term statistical data has increased. The

necessity for reliable predictions for weather and

meteorological information about the future

atmospheric state is essential (Kim, 2002).

UM (Unified Model, United Kingdom Met

Office) developed in the UK, is widely used in the

world as a forecast model. However, most of the

NWP models including UM cannot predict wind

speed accurately because of the intense fluctuations

and local variations by region. Therefore, a

compensation technique such as MOS is required to

enhance the accuracy of prediction outputs for

numerical models (Glahn 1972, Termonia 2007,

Vannitsem 2008, Yu 2011). The MOS technique

aims at correcting current forecasts based on

statistical information gathered from past forecasts.

A few indices (temperature, relative humidity, wind

speed and wind direction) are expected to be

improved by the MOS, compared to the UM forecast

alone.

A regression analysis based technique using

MLR, PLSR, and PCR (Palutikof, 2002) was studied

to predict wind speed for a northwest region of

Europe. Prediction method using an improved time

series and Wavelet technique on wind speed and

wind pressure was proposed (Liu, 2009). The linear

regression methods are still widely used in those

systems. The MOS currently used in KMA for short-

range prediction of temperature has adopted a linear

regression too.

However, most of the previous approaches are

based on the linear models, there is a limitation in

the optimization of the prediction model. Further, a

linear regression is not adequate to represent non-

linear behaviors between MOS and predictor

variables. Moreover, this approach requires the fixed

and entire number of predictor variables to construct

a regression model regardless of various locations,

Seo, K. and Hyeon, B..

Evolutionary Nonlinear Model Output Statistics for Wind Speed Prediction using Genetic Programming.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 287-292

ISBN: 978-989-758-157-1

287

seasons, and time intervals, but it may not be

efficient to use same and entire variables in the

regression model for different conditions. Therefore,

it has fundamental limitations to manage the highly

complex nature of weather predictions.

Some artificial neural network based approach

was conducted to reduce prediction error for wind

speed (Sweeney, 2011). However, this method can

represent nonlinear behaviors of the model, but it

still requires the fixed and entire number of

variables. Also, it only gives a set of connection

weights among nodes, as a result, which is not

explainable like a black box.

To overcome these problems of existing

approaches, we have proposed a seemingly more

efficient approach that optimizes a compensation

model for temperature predictions through nonlinear

combinations of potential predictors using GP

(Genetic Programming) (Koza, 1992). Genetic

Programming is an evolutionary optimization

technique based on Darwinian principles, which

enables to represent the flexible structures of the

model. GP based nonlinear regression can

effectively search open-ended space for order and

coefficient of equations with smaller variables. It is

also a powerful means to generate open-ended high-

order equations and complex nonlinear forms using

transcendental functions. This allows it to solve the

limitations of a linear regression model.

In this paper, a generation technique of the

nonlinear regression model for MOS using Genetic

Programming is proposed. A GP based symbolic

regression approach is used to perform a nonlinear

regression for correcting (or compensating) a wind

prediction model. This paper is organized as follows.

Section 2 introduces a genetic programming based

method for non-linear MOS. Section 3 describes a

notion of numerical weather prediction. Section 4

presents experimental results of temperature forecast

for Korean regions by the proposed GP_MOS

method, and Section 5 concludes the paper.

2 AWS, UM, AND MOS

2.1 AWS

An AWS (Automatic Weather Station) is to enable

measurements for weather elements from remote

areas. An AWS will typically consist of a weather-

proof enclosure containing the data logger,

rechargeable battery, telemetry and the

meteorological sensors with an attached solar panel

or wind turbine and mounted upon a mast. Most

automatic weather stations have a thermometer for

measuring temperature, anemometer for measuring

wind speed, wind vane for measuring wind direction,

hygrometer for measuring humidity, and barometer

for measuring atmospheric pressure. 600 AWSs are

available in South Korea as shown in Figure 1

(Korea Meteorological Administration). Darker

colors mean higher altitude.

Figure 1: Map of AWS stations in Korea.

2.2 UM

The UM (Unified Model) is a numerical weather

prediction and climate modeling tool originally

developed by the United Kingdom Met Office, and

now both used and further developed by many

weather-forecasting agencies around the world.

Table 1: Potential Predictors.

Types Potential Predictors

Air Temperature TS, T8, T7, T5

Thickness DZ18, DZ17, DZ85

Dew-point

TDD8, TDD7,

TDD5

Relative humidity RH8, RH7, RH5

Mean RH

MRH17, MRH15,

MRH85

Zonal wind US, U8, U7, U5

Meridional wind VS, V8, V7, V5

Wind speed

WSS, WS8, WS7,

WS5

Wind direction

WDS, WD8, WD7,

WD5

Lapse rate LR87, LR85

Total rain amount(3hr

accumulated)

PCP

Etc. KI, SWTI

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

288

The KMA (Korea Meteorological Administration)

has an operational 12km resolution global

forecasting system utilizing the Unified Model. The

UM is run twice a day (00 and 12 UTC) producing

forecasts from 6 hours to 66 hours at a 3 hours

interval. The total 37 potential predictors of UM that

were employed in our work including temperature,

humidity, wind speed and accumulated rainfall as

shown in Table I.

2.3 MOS (Model Output Statistics)

Numerical weather prediction models contain

numerous parameterizations for physical processes

and numerical stability. Parameterizations are based

on physical laws, but typically contain parameters

whose values are not known precisely.

The MOS technique aims at correcting current

forecasts based on statistical information gathered

from past forecasts. In its most popular form, it is

based on a linear relation between the reference

variables that we want to predict a set of model

predictors at a certain lead time The MOS currently

used in KMA for short term prediction of

temperature has adopted a linear regression with

equation (1). It consists of a linear combination of

predictors (or predictor variables). It is a

compensated amount for the corrected forecast.

∆WSS















⋯







(1)

where, 



, i=1, …, N, represents one of the

potential predictors in Table 1.

As before mentioned in the introduction, one of

the problems with this method is that the entire large

number of predictor variables should be included to

construct a MOS model for diverse situations. It may

be suffering from multicollinearity which the

coefficient estimates of the multiple regression may

change erratically in response to small changes in

the model or the data by multiple predictor variables

in a regression model are highly correlated. The

other problem is that the above linear operation is

inappropriate to model non-linear relationships

between the MOS for temperature prediction and its

predictor variables.

3 GENETIC PROGRAMMING

BASED MODEL OUTPUT

STATISTICS

In recent years, evolutionary optimization

techniques based on Darwinian principles have

become popular to solve complex NP hard problems.

Genetic programming is an extension of the genetic

algorithm and can manipulate variable-sized entities.

The tree representation of GP chromosomes, as

compared with the string representation typically

used in GA, gives GP more flexibility to encode

solution representations for many model design and

optimization applications.

The GP algorithm starts with an initial

population of arbitrarily generated individuals.

These individuals, represented by trees, consist of

functions and terminals that are suitable for a

specific problem. GP builds new trees by repeatedly

selecting from a function set (the collection of items,

which may appear as nodes in a tree) and stringing

them together. The termination criterion may include

a maximum number of generations to be run as well

as a problem-specific success predicate. Next, each

individual of the population is classified by a fitness

function that is defined by the programmer and

obtains the aptitude of the individual during the

course of its adaptation. As such, a new population

is created by applying the genetic operators of

reproduction, crossover and mutation to individuals

that are selected according to their performance, and

the previous generation is replaced.

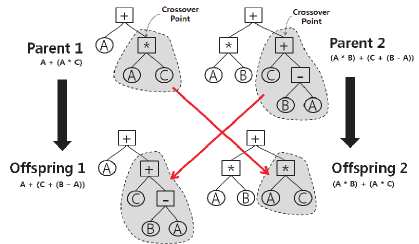
The most commonly used form of crossover is

subtree crossover. Given two parents, subtree

crossover randomly (and independently) selects a

crossover point (a node) in each parent tree. Then, it

creates the offspring by replacing the subtree rooted

at the crossover point in a copy of the first parent

with a copy of the subtree rooted at the crossover

point in the second parent, as illustrated in Figure 2.

The most commonly used form of mutation in GP

(which we will call subtree mutation) randomly

selects a mutation point in a tree and substitutes the

subtree rooted there with a randomly generated

subtree. This is illustrated in Figure 3.

An example of GP MOS regression by the GP

tree is shown in Figure 4. Compared to the equation

(1) of the linear regression, a GP based MOS can

Figure 2: Crossover operation of GP.

Evolutionary Nonlinear Model Output Statistics for Wind Speed Prediction using Genetic Programming

289

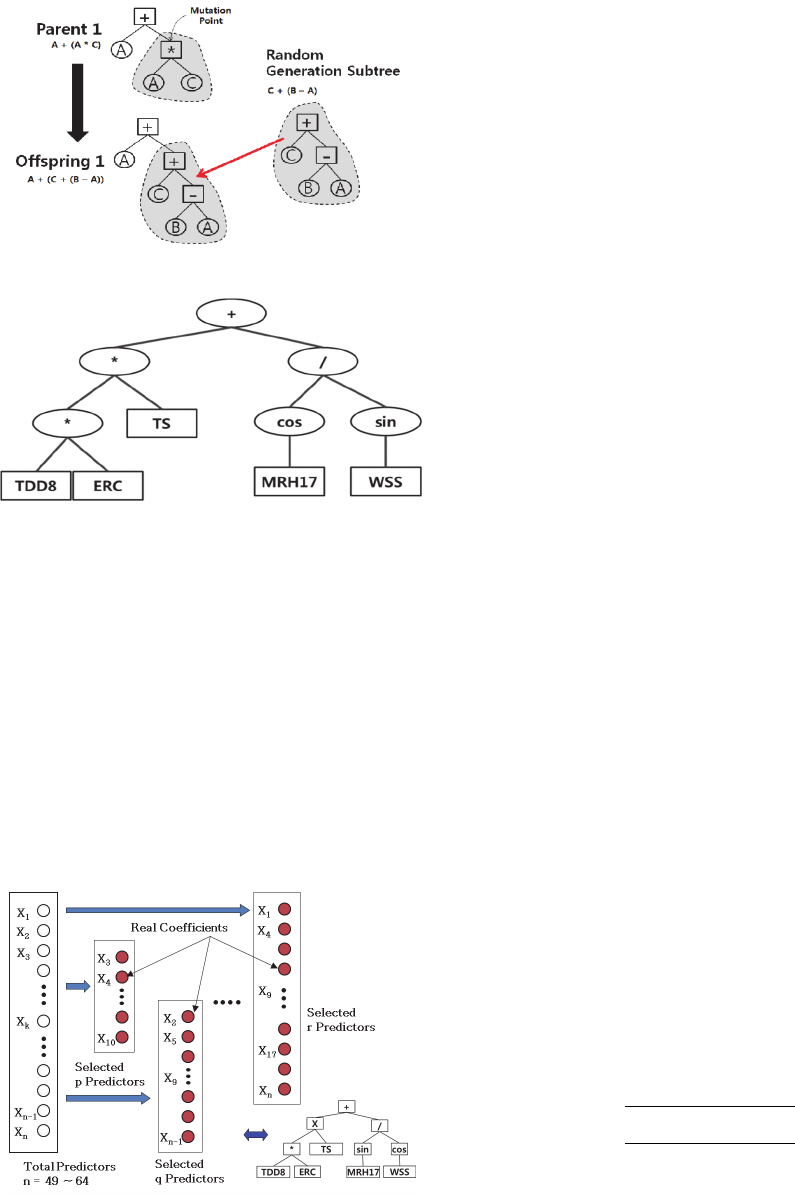
Figure 3: Mutation operation of GP.

Figure 4: Example of an individual by GP tree.

express nonlinearity much more flexible by

involving multiplication, division, sinusoidal

functions, and user defined functions. Therefore, it is

possible to generate open-ended high-order

equations and complex nonlinear forms using a tree

structure. It allows to solve the limitations of a linear

regression approach also.

Especially, the fundamental problem of pre-

selection for potential predictors can be naturally

solved in the GP based approach, since dominant

predictors are extracted automatically through the

evolution process of genetic programming. That

means all candidates of predictors are considered

without excluding some potential predictors in

Figure 5: Natural Selection of Predictors in GP

Evolutionary Process.

advance. Therefore the possibility of optimized

selection of potential predictors is much higher than

in the case of predetermined predictors.

Every solution of the GP based MOS does not

necessarily have the same predictors, because not

only the size and shape of the GP tree for optimized

solutions are different but also selected predictors

are varied for each solution. Therefore, we can

generate a tailor-made compensation equation for

various locations in a wide range of periods which

have different characteristics. The natural selection

by evolutionary process is illustrated in Figure 5.

4 EXPERIMENTS AND RESULTS

4.1 Experimental Setup

The GP programs were run on a Intel Core I7 3770

3.4GHz with 8GB RAM using lil-gp (Zongker

1995). The GP parameters used for the GP_ MOS

generation were as follows:

Population sizes: 200

Max generation: 200

Initial Tree Depth: 2-3

Initial Tree Method: Half and Half

Max Depth: 10

Crossover Rate: 0.9

Mutation Rate: 0.1

The function set for the proposed GP-based

MOS involves following 6 arithmetic operators, and

the terminal set includes 64 potential predictors as

shown in Table 1.

Function = {+, *, -, /, avg, wf1, wf2, cosine, sine}

Terminal = {64 predictor variables}.

The set of primitive functions should be

sufficient to allow for a solution of the problem at

hand, but there are typically many possible choices

of operators-sets that meet this condition. Through

preliminary experiments, the function set above is

selected. Here, avg denotes the arithmetic mean of

two variables, wf1 and wf2 are the weighted sum of

two predictor variables, wf1 uses 0.3 for the first

variable and 0.7 for the first variable, wf2 uses 0.4

and 0.6.

fitness



∑



















(2)

_



_



∆_



The fitness function of the GP based wind speed

prediction is defined to minimize the RMSE (Root

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

290

Mean Square Error) for temperature prediction

between KLAPS reference data and forecast data

obtained by the GP based compensation technique.

It is described in equation (2), where WSS_UM

i is

the wind speed obtained by UM.

4.2 Experimental Results

Performance indices of RMSE(Root Mean Square

Error), ME(Mean Error), and MAE(Mean Absolute

Error) are calculated for comparisons between the

linear regression method and the proposed GP

method. The total average results of all 600 locations

for the test period show that the nonlinear GP

method is superior to the linear regression method in

most of the indices as we expected. The average

RMSE of GP is 1.615 and Linear Regression is

2.556, showing an improvement of 36.8%, both are

better than of UM remarkably. Although the average

BIAS of GP is 0.387 which is a little larger than

0.279 of Linear Regression, the MAE of GP 1.201

is far better than of the respective value of the linear

regression method. The summary of comparison

results is shown in Table 2.

Table 2: Summary of Comparisons for RMSE among UM,

Linear, Regression and GP.

RMSE

(SD)

min ~

max

BIAS

(SD)

min ~

max

MAE

(SD)

min ~

max

4.215

(1.558)

1.085~

7.433

-2.565

(2.239)

-6.487~

5.965

3.420

(1.352)

0.791~

6.493

UM +

Linear Reg.

2.556

(0.709)

0.883~

7.3

0.279

(0.805)

-4.069~

6.372

1.938

(0.577)

0.536~

6.392

UM + GP

1.615

(0.599)

0.439~

4.816

0.387

(0.544)

-4.026~

1.201

(0.466)

0.273~

4.06

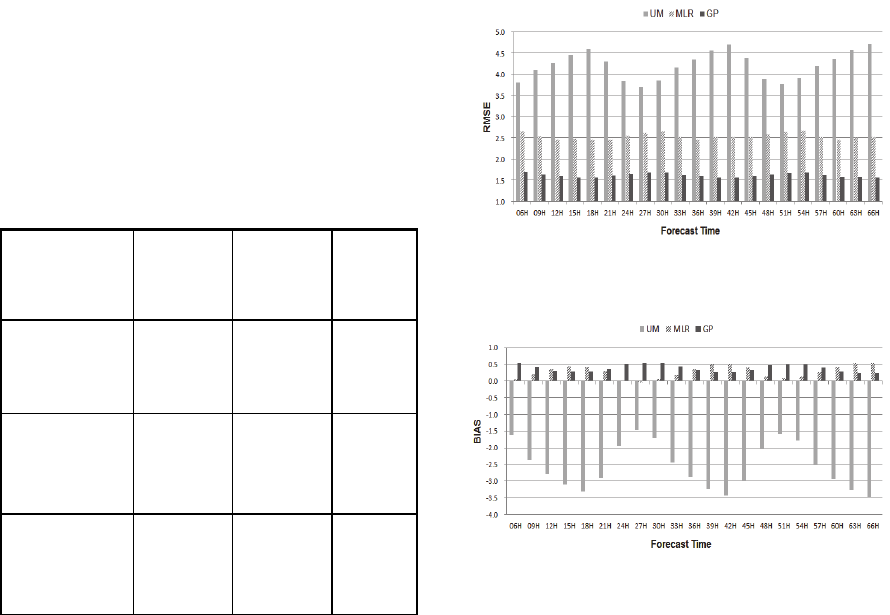
The comparison results of average RMSE in the test

experiment for 12 UTC among UM, MLR and

GP_MOS forecast every 3 hours are shown in

Figure 6. The numeric results represent

performances among UM, Linear Regression and

GP-MOS comparing with KLAPS reference data for

21 intervals from +06h to +66h. It is shown that that

the average RMSEs of GP for 3-days (06h~66h)

forecast intervals are also is better than of UM and

MLR. The ranges of maximum and minimum

deviations for RMSE of GP are far less than of UM

and MLR in all the time intervals.

Interestingly, the wave pattern of results by time

occurs periodically. RMSE values of UM in the

night and morning time (+18h, +39h~45h,

+63h~66h) are higher than others. It was found that

RMSE values of GP and MLR are less susceptible to

the forecast time period and show slightly opposite

wave patterns compared to that of UM.

Figure 7 shows the comparisons of average

BIAS among UM, MLR and GP for 3-days forecast

intervals. The BIAS of UM is in the negative

direction, BIAS of MLR and GP are in the positive

direction. The BIAS values of GP are a little larger

than of MLR, though different in each interval, but

are distributed quite lower than that of UM.

Figure 6: RMSE of Wind Speed prediction for UM, MLR

and GP in entire AWS locations at 12 UTC.

Figure 7: BIAS of Wind Speed prediction for UM, MLR

and GP in entire AWS locations at 12 UTC.

5 CONCLUSIONS

In order to improve wind speed prediction, a new

nonlinear MOS technique, based on symbolic

regression using Genetic Programming, has been

proposed and compared to a linear regression

method. Enormous experiments were executed for

600 AWS locations in South Korea with 21 intervals.

Evolutionary Nonlinear Model Output Statistics for Wind Speed Prediction using Genetic Programming

291

Learning was performed in the period of 2007-2009,

2011 year is used, the data of 2012 year is for

verification, and 2013 year is adopted for test. The

GP method showed superior results than the results

of linear regression method in average RMSE and

MAE.

It becomes clear that the proposed GP based

method is quite competitive with the results of linear

based MOS used in KMA. Further study will aim at

the refinement of the predictor and operator

selection and improvement Evolutionary search

process. This provides some support for the

conjecture that nonlinear and open-ended MOS will

be a promising approach for weather prediction.

REFERENCES

Glahn, H. R. and Lowry, D. A.: The use of model output

statistics (MOS) in objective weather forecasting, J.

Appl. Meteor., 11, 1203–1211, 1972.

Korea Meteorological Administration, http://

www.kma.go.kr.

Koza, J. R.: Genetic Programming: On the Programming

of Computers by Natural Selection, MIT Press,

Cambridge, 1992.

Kim, Y.-S., Park, O.-R., and Hwang, S.-O.: Real time

Operation of the Korea Local Analysis and Prediction

System at METRI, Asia-Pacific J. Atmos. Sci., 38, 1-

10, 2002.

Liu H., Tian H., Chen C., Li Y.: A hybrid statistical

method to predict wind speed and wind power,

Renew. Energ., 35, 1857-1861, 2009.

Palutikof, J. P., Holt, T., Osborn, T.J.: Seasonal

forecasting of strong winds over Europe, Symposium

on global change and climate variations, vol. 13, 125-

128, 2002.

Sweeney C. P., Lynch P., Nolan P.: Reducing errors of

wind speed forecast by an optimal combination of

post-processing methods, Met. Apps, 20, 32-40. 2011.

Termonia, P. and Deckmyn, A.: Model-inspired predictors

for model output statistics, Mon. Weather. Rev., 135,

3496–3505, 2007.

United Kingdom Met Office’s website : http://www.

metoffice.gov.uk.

Vannitsem, S.: Dynamical Properties of MOS Forecasts:

Analysis of the ECMWF Operational Forecasting

System, Weather Forecasting, 23, 1032-1043, 2008.

Yu, X., Park, S.-K., Lee, Y.-H., Ahn, K.-D., and Choo, S.-

H.: The gridding of MOS for high resolution

forecasting, The fifth Korea-Japan-China Joint

Conference on Meteorology, 18-21, 2011.

Zongker, D. and Punch, B.: Lil-GP User’s Manual,

Michigan State University, 1995.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

292