Knowledge Discovery and Modeling based on Conditional Fuzzy
Clustering with Interval Type-2 Fuzzy
Yeong-Hyeon Byeon and Keun-Chang Kwak
Department of Control and Instrumentation Engineering, Chosun University, Gwangju, Korea
Keywords: Knowledge Discovery, Linguistic Modelling, Conditional Fuzzy Clustering, Interval Type-2 Fuzzy.
Abstract: This paper is concerned with a method for designing improved Linguistic Model (LM) using Conditional
Fuzzy Clustering (CFC) with two different Interval Type-2 (IT2) fuzzy approaches. The fuzzification factor
and contexts with IT2 fuzzy approach are used to deal with uncertainty of clustering,. This proposed
clustering technique has characteristics that estimate the prototypes by preserving the homogeneity between
the clustered patterns from the IT2-based contexts, and controls the amount of fuzziness of fuzzy c-partition.
Thus, the proposed method can represent a nonlinear and complex characteristic more effectively than
conventional LM. The experimental partial results on coagulant dosing process in a water purification plant
revealed that the proposed method showed a better performance in comparison to the previous works.
1 INTRODUCTION
A considerable number of researches have been
performed on fuzzy models during the past few
decades. Such fuzzy models are simply divided into
two types depending on the particular structure of
the consequent part: linguistic fuzzy model and TSK
(Takagi-Sugeno-Kang) fuzzy model. In the
linguistic fuzzy model, Mamdani model was
proposed as the first attempt to control a steam
engine and boiler combination by a set of linguistic
control rules obtained from experienced human
operators. TSK fuzzy model is designed by a
systematic approach to generating fuzzy rules from a
given input-output data set.
On the other hand, we enhance a Linguistic
Model (LM) (Pedrycz, 1999) constructed by the use
of fuzzy granulation performed by Conditional
Fuzzy Clustering (CFC) (Pedrycz, 1996). For this
purpose, we develop the improved clustering
approach based on conventional LM. Although the
superiority of this model has demonstrated in the
previous literatures, this model has a poor
approximation and generalization capability. In
order to enhance this performance, we use Interval
Type-2 (IT2) fuzzy concept (Karnik and Mendel,
1998) to estimate efficient cluster centers.
Furthermore, we deal with knowledge discovery and
linguistic modeling based on three different
uncertainties; fuzzification factor, linguistic contexts,
and both. The proposed method is constructed by
conditional fuzzy clustering with three different
uncertainty types. Finally, we apply to coagulant
dosing process in a water purification plant. The
partial results produced by the proposed method
show a better performance in comparison with
conventional LM.
This paper is organized as follows. Section 2
describes the architecture and context-based fuzzy
clustering for LM. In Section 3, we present the three
different uncertainty types for IT2 fuzzy concept.
Experimental results and comments are covered in
Section 4. Finally, conclusion is given in Section 5.
2 CONVENTIONAL LINGUISTIC
MODEL
The conditional fuzzy clustering is realized by
individual contexts. Each context (fuzzy set) has
defined semantics that can be interpreted as a small,
medium, large in the design of LM. Let us consider
a certain fixed context W
j
described by some
membership function. The data point in the output
space is associated with the corresponding
membership value. Let us introduce a family of the
partition matrices induced by the context and denote
it by U as follows
440
Byeon, Y. and Kwak, K..
Knowledge Discovery and Modeling based on Conditional Fuzzy Clustering with Interval Type-2 Fuzzy.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 1: KDIR, pages 440-444
ISBN: 978-989-758-158-8
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved















c
i
ikik
iandku|,u
1
110U (1)
The underlying objective function is as follows
2
ik
N
1k
m
ik
c
1i
||||uJ vx 


(2)
where
v
i
denotes the i -th cluster center. The
minimization of objective function is realized by
iteratively updating the values of the partition matrix
and the clusters. The updates of the partition matrix
are completed as follows
















c
1j
1m
2
jk
ik
k
l
ik
w
u
vx
vx
,
(3)
where
Nkci ,,2,1,,,2,1  
and u
ik
is the
partition matrix induced by the
l -th context. The
cluster centers are as the follows





N
1k
m
ik
N
1k
k
m
ik
i
u
u x
v
(4)
In the design of the LM, we consider the contexts to
be described by triangular membership functions
being distributed in the output space with the 1/2
overlap occurring between two successive fuzzy sets.
The automatic generation of linguistic contexts is
obtained by the output data density and probabilistic
distribution. We denote those contexts by W
1
, W
2
,
…, W
p
. The output type of LM is granular
presenting the triangular form of the contexts. The
triangular fuzzy number E is expressed as
nn2211
....WWWE  (5)
We denote the algebraic operations by
 and
to
emphasize that the underlying computing operates
on a collection of fuzzy numbers. As such, E is
completely characterized by its three parameters that
are a modal value, the lower, and upper bounds.
3 IT2-CFC APPROACHES
The procedure of the conditional fuzzy clustering
with three IT2 fuzzy approaches (IT2-CFM) is
described. The estimation method of cluster center is
similar to the procedure of CFCM clustering except
for considering uncertainty of contexts and
fuzzification factor on the basis of Interval Type-2
fuzzy set.
3.1 Uncertainty of Fuzzification Factor
(m)
The uncertainty of fuzzification factor in the design
of IT2- CFC is described. This method can control
the amount of fuzziness of fuzzy
c -partition through
the variation of this factor (Rhee, 2007). This factor
exhibits a significant impact on the character of
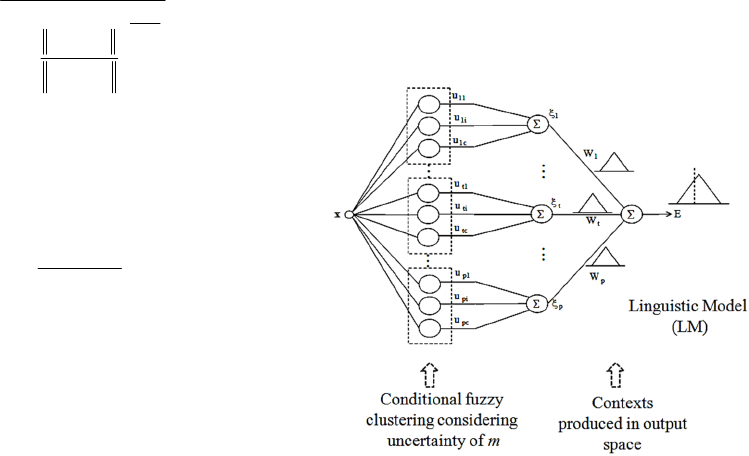
nonlinearity. Fig. 1 shows the architecture of the
proposed LM based on conditional fuzzy clustering
with uncertainty of fuzzification factor on the basis
of IT2 fuzzy concept.
Figure 1: Architecture of the proposed LM.
The IT2-CFC approach considering uncertainty of
fuzzification factor is performed by the following
steps
[Step 1] Select the number of context and cluster per
context, respectively.
[Step 2] Produce the contexts with triangular
membership function using equally
partitioning method in the output space.
Each context is generated by a 1/2 overlap
between successive fuzzy sets.
[Step 3] Compute upper and lower partition matrices
by Eq. (6) and (7). The fuzzification factor
m is replaced by
1
m and
2
m which repre-
sent upper and lower fuzzifier values.
Knowledge Discovery and Modeling based on Conditional Fuzzy Clustering with Interval Type-2 Fuzzy
441






















































c
j
m
jk
ik
k
c
j
m
jk
ik
k
ik
f
f
u
1
1
2
1
1
2
2
1
/
,/
max
cx
cx
cx
cx
(6)





















































c
j
m
jk
ik
k
c
j
m
jk
ik
k
ik
f
f
u
1
1
2
1
1
2
2
1
/
,/
min
cx
cx
cx
cx
(7)
[Step 4] Update the cluster center. The individual
values of the left and right cluster
boundaries in each dimension can be
computed by sorting the order of patterns in
particular dimension and then applying
Karnik-Mendel (KM) iterative procedure
(Karnik, 2001)(Mendel, 2010). Here KM
algorithm is used to update the interval set
of cluster centers. The new cluster center is
computed by a defuzzification method as
follows
2
RL
cc
c


(8)
[Step 5] Compute distance measure between the
updated clusters and the previous ones.
Stop if its improvement over previous
iteration is below a certain threshold.
[Step 6] Compute a new membership function based
on average of lower and upper bound as
type-reduce step Eq. (9). Go to Step 3.
2
ik
ik
ik
uu
u


(9)
3.2 Uncertainty of Contexts (p)
The uncertainty of linguistic contexts produced in
the output space is focused. Fig. 2, 3, and 4 show T1
context with general fuzzy set, IT2 context with
lower and upper bound, and the vertical slice of
output value, respectively. Fig. 5 shows IT2 contexts
produced in the same manner as in conditional fuzzy
clustering. The estimation method of cluster center
is similar to the procedure of CFC algorithm. IT2-
CFC is performed by the following steps.
[Step 1] Select the number of context and cluster per
context.
[Step 2] Generate IT2 contexts with triangular
membership function using equally
partitioning method in the output space.
The upper bound is generated by a 1/2
overlap between successive fuzzy sets. The
left and right lower bounds determine 2/5
value from the center of each triangular
context, respectively.
Figure 2: T1 Context in the output space.
Figure 3: IT2 context in the output space.
Figure 4: Vertical slice of IT2 context in the output space.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
442

Figure 5: IT2 contexts obtained in the output space.
[Step 3] Compute upper and lower partition matrices
as the following Eq. (10) and (11). Here
fuzzification factor is set to m=2.





















































c
j
m
jk
ik
k
c
j
m
jk
ik
k
ik
f
f
u
1
1
2
1
1
2
/
,/
max
cx
cx
cx
cx
(10)





















































c
j
m
jk
ik
k
c
j
m
jk
ik
k
ik
f
f
u
1
1
2
1
1
2
/
,/
min
cx
cx
cx
cx
(11)
[Step 4] Update the cluster center. Firstly, the
individual values of the left and right
cluster boundaries in each dimension are
computed by sorting the order of patterns in
particular dimension. And then KM
procedure is used.
[Step 5] Compute distance measure between the
updated clusters and the previous ones.
Stop if its improvement over previous
iteration is below a certain threshold.
[Step 6] Compute a new membership function. Go
to Step 3.
4 EXPERIMENTAL RESULTS
We apply the proposed method to coagulant dosing
process in a water purification plant (Kwak, 2012).
The field test data of a coagulant dosing process to
be modeled is obtained at the Amsa water
purification plant, Seoul, Korea. We use the 346
samples among jar-test data. The input consists of
four variables. Each variable is the turbidity of raw
water, temperature, pH, and alkalinity. The output
variable to be predicted in terms of the preceding
input attributes is PAC (Poli-Aluminum Chloride)
widely used as a coagulant.
In order to evaluate the resultant model, we
divide the data sets into training and checking data
sets. Here, we choose 173 training sets for model
construction, while the other test sets are used for
model validation. In the case of uncertainty by
fuzzification factor (case 1), this factor is used from
m=1.1 to 5. The experiments were performed with
the range of p=[2 6] and c=[2 6]. In the case 2, we
are currently researching regarding the method to
determine lower and upper bounds of each context.
Thus, we shall focus on the experiment and the
results regarding the only first case in this paper.
Fig. 6 shows the prediction performance of the
proposed model. Table 1 lists the mean of RMSE
(root mean square error) results regarding
approximation and generalization capability,
respectively. It has experimented for p = c = 6 in
which case it has achieved a sound balance between
the granularity of information formed in the output
and input space.
Figure 6: Prediction performance for training and testing
data set.
In the design of LM, six contexts and six clusters
in each context are used. Although the LM has a
structured knowledge representation in the form of
fuzzy if-then rules, it lacked the adaptability to deal
with nonlinear model. As listed in Table 1, the
experimental results revealed that the proposed
model yielded good prediction performance in
1 2 3 4 5 6 7 8
0
0.2
0.4
0.6
0.8
1
membership degree
0 20 40 60 80 100 120 140 160 180
0
20
40
60
No. of training data
PAC
actual output
model output
0 20 40 60 80 100 120 140 160 180
0
20
40
60
No. of test data
PAC
actual output
model output
Knowledge Discovery and Modeling based on Conditional Fuzzy Clustering with Interval Type-2 Fuzzy
443

comparison to the previous works such as Linear
Regression (LR), Neural Networks (NN) of multi-
layer perceptron, Radial Basis Function Networks
(RBFN) (Pedrycz, 1998), and LM(Pedrycz, 1999).
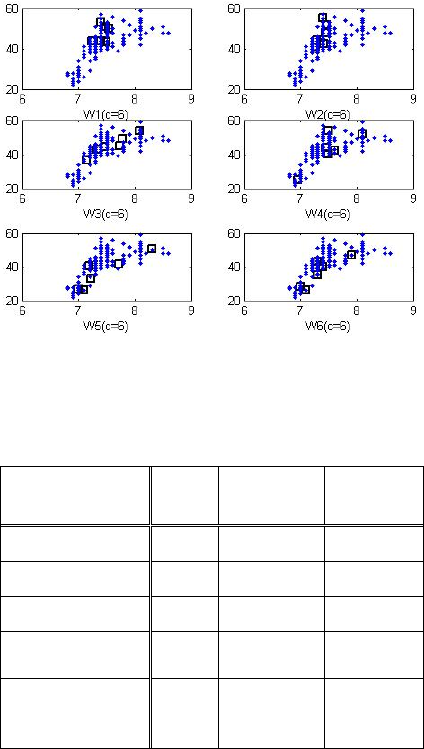
Fig. 7 visualizes the data distribution and cluster
centers estimated in each context for pH(x-axis) and
alkalinity(y-axis).
Figure 7: Data distribution and cluster centers estimated in
each context.
Table 1: Comparison results of RMSE and the number of
rule (* number of node).
Methods no. rule
RMSE
(training)
RMSE
(test)
LR - 3.508 3.578
NN 45* 3.191 3.251
RBFN 45* 3.048 3.219
LM
(p=c=6)
36 3.401 3.455
The proposed
method (case 1)
(p=c=6)
36 2.832 2.989
5 CONCLUSIONS
We have developed the design method of the
improved LM based on two IT2-CFC algorithms
with uncertainty of fuzzification factor m. The
proposed clustering algorithm includes the
characteristics both uncertainty of fuzzification
factor and the homogeneity between the clustered
patterns, and controls the amount of fuzziness of
fuzzy partitioning. For further research, it will focus
on the uncertainty of both fuzzification factor and
linguistic contexts. Furthermore, the genetically
optimization to determine the number of cluster and
context in the design of LM using IT2-CFC
algorithm will be considered.
ACKNOWLEDGEMENTS
This research was supported by Basic Science
Research Program through the National Research
Foundation of Korea (NRF) funded by the Ministry
of Science, ICT and Future Planning (NRF-
2013R1A1A2012127)
REFERENCES
Karnik, N. N, Mendel, J. M., 1998. An Introduction to
Type-2 Fuzzy Logic Systems, Univ. of Southern
California, Los Angeles, CA
Rhee, F. C. H., 2007. “Uncertain fuzzy clustering: insights
and recommendations”, IEEE Computational
Intelligence Magazine, Vol. 2, No.1, pp.44-56.
Karnik, N. N. Mendel, J. M., 2001. “Centroid of a type-2
fuzzy set”, Information Sciences, Vol. 132, No. 1,
pp.195-220.
Pedrycz, W., 1996. “Conditional fuzzy c-means”, Pattern
Recognition Letter, Vol.17, pp.625-632.
Pedrycz, W., 1998. “Conditional fuzzy clustering in the
design of radial basis function neural networks”, IEEE
Trans. on Neural Networks, Vol. 9, No. 4, pp. 601-
612.
Pedrycz, W. and Vasilakos, A. V., 1999, “Linguistic
models and linguistic modeling”, IEEE Trans. on
Systems, Man, and Cybernetics-Part C, Vol. 29, No.6,
pp.745-757.
Mendel, J. M. Wu, D., 2010. Perceptual Computing:
Aiding people in making subjective judgment, Wiley.
Kwak, K. C., 2012, “A design of genetically optimized
linguistic models”, IEICE Trans. on Information &
Systems, Vol. E95-D, No.12, pp. 3117-3120.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
444