A Flexible and Simplified 2D Environment for Evolving Autonomous
Virtual Creatures
Ricardo Sisnett
Riot Games Inc, Los Angeles, U.S.A.
Keywords:
Artificial Life, Genetic Algorithms, Neural Networks, Evolutionary Computing.
Abstract:
In this paper we present a method for creating two-dimensional virtual creatures. Their shape and controlling
systems are generated automatically by the use of a genetic algorithms. Unlike previous work, our system has
an emphasis in approachability and simplicity, but sacrifices simulation realism. This trade off is done with
the intention of using the framework for highly interactive applications such as video games or exhibits.
1 INTRODUCTION
Systems that develop and evolve morphology and
control of virtual creatures is a topic that has been
visited several times in the past. From the seminal
work of Karl Sims (Sims, 1994) to the work in soft
and 3-D printed robots at the Creative Machines Lab
at Cornell (Cheney et al., 2015) (Shen et al., 2012)
some enormous strides have been made in the area,
proving that both 3D and 2D creatures can be evolved
to solve a variety of problems in diverse scenarios.
However, most of these experiments are hard to ap-
proach due to their technical nature, and very few
of the results are taken outside the laboratories to
wider audiences. Galapagos (Sims, 1997) and End-
lessForms.com (Clune et al., 2011) are probably two
of the clearest attempts of taking experimental results
and expose them to a wide audience in an interactive
fashion.
On the other hand, and for some time now, vir-
tual pets and companions have become parts of popu-
lar culture, from Tamagotchis and Furbys to Pokemon
and NeoPets, all of these have been very well received
by really wide audiences, however their relations with
real evolutionary and biological cycles is pretty small.
Even though both, wide-reaching virtual compan-
ion products and evolutionary methods for creating
virtual creatures, have been successful separated, very
few attempts to close the gap between them. Spore
was a high profile project that promised a lot in the
areas of interactive virtual life; but it is seen mostly
as failing short on its initial promise: ’evolution’ was
just a traditional RPG progression system and all con-
tent was user generated losing a big opportunity to
explore artificial life in the context of video games.
This work aspires to take off where Galapagos
left, and grabs concepts from game design to allow the
results to be more approachable and usable in other
areas, mainly concerned with entertainment and inter-
active education. Polyminis, the first installment and
baseline for the framework presented, uses an aes-
thetic borrowed from the classic game Tetris, mainly
to lean into familiarity and spark interest from audi-
ences and collaborators outside of the usual commu-
nities involved in artificial life experiments.
2 CREATURE MORPHOLOGY
The name Polymini comes from the term ”poly-
omino”, defined as ”a plane geometric figure formed
by joining one or more equal squares edge to edge”,
concept which inspires the creature’s prototypical em-
bodiment: that of an N-Polyomino.
A Polyminis genotype is an encoded directed
acyclic graph (DAG) where each vertex of the graph
represents a cell (square) in the creature’s phenotye.
Unlike most experiments in the area (Ventrella, 1999)
(Sims, 1994), the gene does not encode shape for the
pieces in the Polymini, all the parts conforming the
final genotype are the same size and shape, however
their function is encoded in the gene and each cell
adds to the overall capabilities of the creature. In ad-
dition to function and form, cosmetic information is
also part of the genotype, namely the overall color of
the creature, per-cell color variations and per-cell UV
coordinates to a texture.
306
Sisnett, R..
A Flexible and Simplified 2D Environment for Evolving Autonomous Virtual Creatures.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 306-312
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

A population of Polyminis is evolved in a scenario.
A scenario is conformed by a set of obstacles, a fit-
ness function and a translation table. The translation
table maps the genetic information from the genotype
into the specific cell of the phenotype. The concept
of the translation table and the mechanisms of trans-
lation are further explained in section 2.4.
Three main types of cells can be evolved by the
creature: Actuators, Sensors and Traits.
2.1 Actuators
An actuator gives the Polyminis the ability to inter-
act with the world in some way, and change the cur-
rent state of itself and/or its environment. Actuators
are tied into the creature’s control system, and re-
ceive stimuli from the neural network output layer.
The most obvious example of actuators are movement
cells, which allow the creature to vary it’s position and
orientation over time. Details on the control system
can be found in Section 3
2.2 Sensors
A sensor gives the creature information about its cur-
rent state and that of the environment. Sensors pro-
vide stimuli to the control system, serving as the input
layer of the neural network.
2.3 Traits
Some cells provide traits that fall outside of the con-
cepts of actuator or sensor. The only example of this
type of cell used in the experiments described in 6 is
a ’speed’ trait, that increases the number of sensing-
actuating cycles the creature can effectuate, allowing
it to move more often than other creatures and cover
greater distances.
2.4 The Translation Table
The translation table is an idea born of combining
the biological concept of DNA/RNA translation ta-
bles (Eiben and Smith, 2003) and budget based pro-
gression tables common in RPG games (Zagal and Al-
itzer, 2014).
At the time of conversion from genotype to pheno-
type, the translation table is used to decide which type
of cell is to be created in the current position. The al-
gorithm that does the translation can be summarized
as follows:
func decode(genotype):
gene = null
level = 1
while ( not_empty(genotype) ):
gene = get_next_gene(genotype)
if ( gene equals chaining_sequence ):
level = level + 1
else:
create_cell(level, gene)
level = 0
endif
endwhile
endfunc
The concept of a ’chaining sequence’ allows the
creation of a hierarchy of traits, in which some are
harder to develop than others, and require a bigger
investment of genetic material to achieve. Scenar-
ios register traits at the desired level and a probability
factor, the translation table then creates a distribution
function based on the maximum number of traits per
level and those factors. By default the probability of
each trait per level is defined by the following equa-
tion:
P
t
=
1
2
g
∗ f (1)
Where g is the length of the gene and f is the prob-
ability factor. Table 1 presents an example of a trans-
lation table.
3 CREATURE CONTROL
Each Polymini has an associated brain that each simu-
lation step queries the sensing cells and stimulates the
actuation cells. For the first version of the framework,
the brain is a simple multilayer perceptron (MLP)
(Haykin, 1998) composed by one input layer (sen-
sors), one hidden layer, and one output layer (actu-
ators). The parameters of the MLP that are evolved
through the genetic algorithm are the weight of the
connections between layers and the size of the hidden
layer.
Although the MLP brain has been sufficient for
the experiments presented in 6, future work could po-
tentially focus on diverse types of neural networks
and neural network generation methods such as those
described by (Kitano, 1990) and comparisons among
them.
4 EVOLUTION
Both morphology and control of the Polyminis are
evolved using a traditional genetic algorithm (Gold-
berg, 1989).
A Flexible and Simplified 2D Environment for Evolving Autonomous Virtual Creatures
307
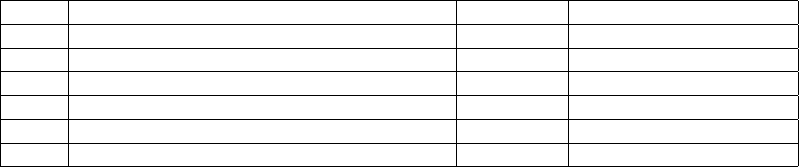
Table 1: An example of a translation table. Usinga 4 bit long gene (g = 4) and a probability factor of 2 for all traits but the
chaining sequence (f = 2). All other gene sequences yield a traitless cell, or structural cell as we refer to them.
Level Trait Probability Gene Sequences Matched
N/A Chaining Sequence 0.0625 1111
1 Vertical Movement Actuator 0.125 0000, 0001
1 Horizontal Movement Actuator 0.125 0010, 0011
1 Speed Trait 0.125 0100, 0101
2 Horizontal Movement Actuator + Speed Trait 0.125 0000, 0001
2 Vertical Movement Actuator + Speed Trait 0.125 0010, 0011
4.1 Morphology
For genetic operations on the morphology, the ADG
is encoded as a byte stream. During sexual repro-
duction, the parents byte streams are cut at arbitrary
points and the pieces put together. There is no val-
idation done on the resulting graph, and it is left to
the translation mechanism to ignore and/or any con-
tradictions that arise, like 2 cells trying to take the
same physical space. Due to this, pieces of the geno-
type can become inaccessible (i.e. not read during the
translation process), however this is desirable since
it is analogous the concept of non-coding or ’junk’
DNA and can still be rediscovered by future genera-
tions.
Mutation occurs on the moment of reproduction
by flipping random bits in the byte-stream. Effects of
such a mutation can have minimal impact on the crea-
ture, like changing the color shade of one cell, mod-
erate impact, like changing the type of cell encoded
in that position, or be really impactful, like rediscov-
ering inaccessible genetic material.
Although for the experiments run as the base-
line for the framework the simple direct encoding is
enough and comes up with diverse yet consistent so-
lutions, direct encoding tends to be volatile and has
a hard time coming up with symmetric and repeat-
ing patterns, as shown in (Cheney et al., 2013), this
could limit the complexity of the problems that could
be tackled by the framework. This is could be a big
area of focus for future work.
4.2 Control
As described in 3 the weights of the neural network
and the size of the hidden layer are encoded and
evolved by the genetic algorithm. The control sys-
tem is generated after the creature morphology has
been extracted from the genotype, since the amount
of sensors and actuators influence the final shape of
the neural network.
During reproduction, the new individual’s brain is
created using one of the following techniques:
1. Single Parent - One of the parents is selected and
its brain is copied over to the new individual.
If the individual requires more connections than
the parent (i.e. has more sensors/actuators) the
new weights are initialized to a small randomized
value [-0.05, 0.05].
2. Single Parent with Grafting - Similar to the pre-
vious one, but new weights are initialized from
information of the parent that was not selected.
Mutation for the control genotype consists of
adding a small value to one or more of the neuron
connections or altering the size of the hidden layer.
Specific behaviors are encoded in the weights of
the neuron connections, given that this weights are in-
herited by new generations those behaviors are passed
as well and albeit simple, this suffices for the base-
lines experiments. The control system suffers from
the same short comings of its morphology counter-
part, using direct encoding in neural networks can
have a negative impact in the overall search, as men-
tioned in (Kitano, 1990). Future work should focus
on implementing a more robust control system, and
compare results .
5 SCENARIOS
The idea of a scenario is pretty similar what has
been done in ”FramSticks”(Komosinski, 2005) envi-
ronments and ”Morphocosmos”(Pilat, 2009), and the
main motivation is to allow easy iteration in artifi-
cial life experiments. A newcomer can design and
run an experiment just interacting with the scenario
object and a fairly narrow Application Program In-
terface (API). Aspirationally, we would like to lower
the entry bar even more, and provide tools to the user
to avoid programming as a requirement altogether.
Tools like Unreal 4 Blueprints (EpicGames, 2014) or
Unreal 3 Kismet (EpicGames, 2012) would be excel-
lent inspirations to allow experiments to be created
without the need of a programming language.
A scenario can be defined as a confined 2D space
described by a 4-Tuple :
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
308
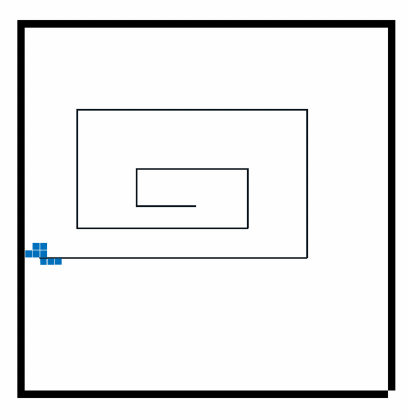
Figure 1: A scenario with a Polymini in it and the route it
followed after a few simulation steps. The fitness function
rewards exploration of the scenario, the generation function
creates the enclosing cage. The translation table used is the
same as the one presented in Table 1.
• A fitness function to guide evolution.
• A set of generation functions for obstacles.
• A translation table.
• A set of functions that generate stimuli each crea-
ture gets despite of the amount of sensors they
evolve.
A scenario can create a population from scratch,
or seed itself with results of other runs.
5.1 Simulation
As mentioned before, the project sacrifices simulation
realism to emphasize in aesthetics and approachabil-
ity, and for those described in Section 6 the aesthetics
and simulation themes are borrowed from the classic
game Tetris (Pajintov, 1984).
The simulation runs in a 2D discrete grid space,
in which the minimum step is the size of a Polyminis
cell. A concept of speed is introduced, allowing some
individuals to act more often than others. An upper
bound is set in the maximum of simulation steps be-
fore resetting the action count, making speed above
that number effectively useless.
In these scenarios, actuators work as small one-
dimensional thrusters and each simulation step in
which the individual can take an action the value in
the output neuron attached to the actuator is added
as impulse. Torque is also calculated using the root
square as the rotation point; this allows the creature to
rotate 90°at a time. In both cases, rotation and trans-
lation, an impulse threshold needs to be broken before
any movement happens.
6 EXPERIMENTS
This section describes the experiments used to vali-
date the system, are established as the first milestone
of the project. Unless otherwise noted, the experi-
ments use the translation table presented in Table 1,
have a maximum simulation speed of 3 and use the
following default inputs:
1. x-position - Current horizontal position of the
creature (Normalized).
2. y-position - Current vertical position of the crea-
ture (Normalized).
3. orientation - Current orientation. Assuming the
orientation obtained of parsing the morphology
genotype is the 0°rotation. (Normalized).
4. last-move-succeded - 0 If last movement attempt
was prevented by a collision, 1 if last movement
was successful.
6.1 Motion Experiments
These experiments focus on the motion capabilities of
the creature and the ability to sort obstacles.
6.1.1 Longest Distance from Starting Point
In this experiment the fitness value for an individual
is the distance between its starting point and where it
is when the simulation ends. A simulation ends 100
steps after, or if the individual does not move during
two immediate simulation steps.
6.1.2 Largest Amount of Different Positions
Visited
A glimpse of this experiment is presented in Figure 1.
The fitness value for each individual is the amount of
different positions visited during the simulation. This
simulation lasts for 150 steps, or until the individual
comes to a stop. Small fitness points are awarded for
movement to encourage it in earlier generations. It
can be observed that a spiral motion is consistently
discovered by the creatures (Figures 1 and 4), which
is the an optimal and simple solution.
6.1.3 Shortest Amount of Time to the other Side
Fitness for this experiment equals the amount of dis-
tance covered in the simulation time plus a multiplier
A Flexible and Simplified 2D Environment for Evolving Autonomous Virtual Creatures
309
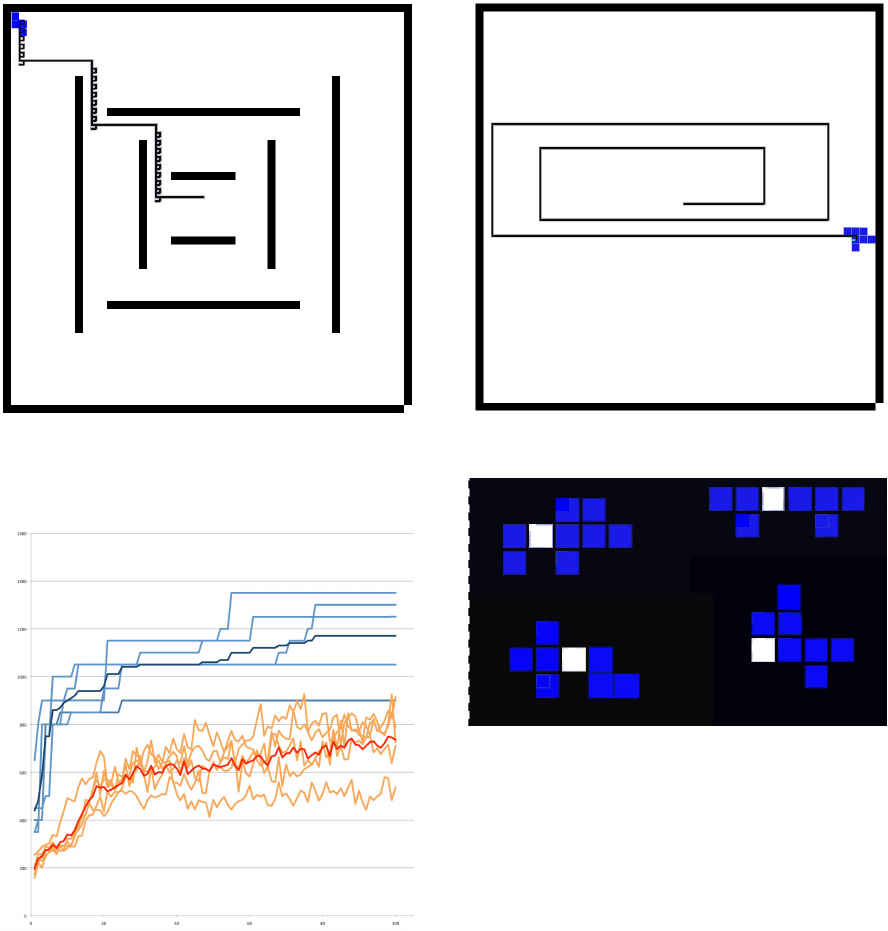
Figure 2: A Polymini solving the hardest version of the
longest distance from starting point scenarios. The square
loops in the line represent instances of the simulation where
the Polymini collided and changed directions.
Figure 3: Comparison of several runs of the maze solving
polymini. The upper (blue) lines represent the maximum
fitness per generation. The lower (orange) represents the
average of the population. The darker lines represent the
averages of the runs.
for reaching the goal. If aPolymini reaches the goal,
fitness of other creatures is divided depending on their
relative placement against the first place. Besides the
obvious development of several speed cells, an inter-
esting pattern that arises is that creatures in this sce-
narios tend to be elongated, this gives them a real
competitive advantage since they can reach the goal
in less movements.
Figure 4: An optimal solution to the ’Largest Amount of
Different Positions Visited’ experiment.
Figure 5: Several champions of the scenario described in
section 6.1.3. The white square represents the origin of the
creature, any square to the right of it represents a competi-
tive advantage.
6.2 Appearance Experiments
These experiments focus on evolving aesthetics or
shape of the creature, and not so much their control
system.
6.2.1 Camouflage
Two color-based experiments in which the Polyminis
have to change their colors:
• Target Color: In the first stage, target color, the
individuals have to evolve their color to match one
given by the environment. The evaluation is the
accumulated difference of each individual’s cell
and the target color. Some weight is given to the
Polymini’s size, i.e., number of cells, to encourage
multi-cellular organisms. This weight decays with
each new cell to prevent unbounded growth.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
310
• Color Tiles: The second stage, color zones, cre-
ates many colored tiles. The Polyminis need again
match a target color. This is with the added dif-
ficulty of having to move to the tile of the tar-
get color. Individuals evaluation happens at each
step of the simulation. The same method as in
stage 1) evaluates them when they are standing
on the right color tile. Polyminis get a penal-
ization if they stand in the wrong tile. This re-
ward/punishment increments with the indiviual’s
sequential successes or misses. At the end of the
run, the mean evaluation determines the fitness for
the Polymini. A new color sensor was added to
this stage to allow the creature to sense the color
of the tile they were standing on, for this effect the
translation table used in this scenario was identi-
cal to Table 1 except a the new color sensor was
added with the same probability factor in the first
level. An interesting avenue to expand this work
would be adding a color actuator that allows the
Polymini to change cell colors during the simula-
tion, achieving camouflage capabilities similar to
the octopus.
6.2.2 Matching Shapes
Exploratory experiments were done on shape match-
ing, mainly as an exercise to on board new collabora-
tors due to the simple nature of the problem.
7 FUTURE WORK
It was mentioned at the beginning that this work cov-
ers only the proof of concept and feasibility study of
the original idea, so a lot of directions could be taken
from this point. The most obvious extension to this
work is to increase the variety of sensors, actuators
and traits the creatures can evolve, as well as the sce-
narios in which they develop. Another direction we
would like to explore is to use coarse grain parallelism
and explore the effects of specialization, migration
and isolation (Kazunori, 2008) (Sisnett, 2012). Co-
evolution and competition are areas that could easily
be explored using this framework as well. Other re-
search vectors that have had some success and would
fit in the scope of the framework are energy or feeding
systems, to encourage simpler more efficient designs
or inclusive food-chains; crowdsourcing evaluation of
aesthetics or social interactions could allow for a large
audience engagement (Orkin, 2013)). Work to create
tooling for scenario creation and management as well
of analytics of populations would go a long way into
achieving the goal of multi-disciplinary engagement
with the project.
8 CONCLUSIONS
After the first stage of the project, we have proved
that the framework can evolve both morphology and
control of creatures to achieve high-level goals. Pat-
tern discovery and refinement can be observed in the
Polyminis even after very few iterations. Investment
in systems that allow the involvement of a wider
amount of disciplines and interest levels will allow
the exploration of barely touched areas of Evolution-
ary Computing, such as the overlap between it and
art or the opportunities in assisted game design and
creature creation. We believe exposing this tooling
and framework to this other disciplines will allow the
framework to grow into areas of interactive simula-
tions.
ACKNOWLEDGEMENTS
The author would like to thank Riot Games Inc, for
the support on this project. The University Of South-
ern California Games Pipe Lab for providing feed-
back in the early stages of the project, and Jorge Issa
and Ricardo Rey from Oracle MDC for their help in
the development of experiments.
REFERENCES
Cheney, N., Bongard, J., and Lipson, H. (2015). Evolv-
ing soft robots in tight spaces. In Proceedings of the
2015 Annual Conference on Genetic and Evolution-
ary Computation, GECCO ’15, pages 935–942, New
York, NY, USA. ACM.
Cheney, N., MacCurdy, R., Clune, J., and Lipson, H.
(2013). Unshackling evolution: evolving soft robots
with multiple materials and a powerful generative en-
coding. In Blum, C. and Alba, E., editors, GECCO,
pages 167–174. ACM.
Clune, J., Yosisnki, J., Doan, E., Samad, N., Liu, S.,
and Lipson, H. (2011). Endlessforms.com. http://
www.endlessforms.com. Accessed: 2015-08-01.
Eiben, A. E. and Smith, J. (2003). Introduction to Evolu-
tionary Computing. Springer, New York, 2nd edition.
EpicGames (2012). Unreal kismet user guide.
udn.epicgames.com/Three/KismetUserGuide.html.
Accessed: 2015-09-01.
EpicGames (2014). Blueprints visual scripting.
docs.unrealengine.com/latest/INT/Engine/Blueprints.
Accessed: 2015-09-01.
A Flexible and Simplified 2D Environment for Evolving Autonomous Virtual Creatures
311
Goldberg, E. (1989). Genetic Algorithms in Search, Op-
timization and Machine Learning. Addison-Wesley
Professional.
Haykin, S. (1998). Neural Networks: A Comprehensive
Foundation. Prentice Hall PTR, Upper Saddle River,
NJ, USA, 2nd edition.
Kazunori, K. (2008). Asynchronous parallel distributed ge-
netic algorithm with elite migration. In International
Journal of Information and Mathematical Sciences 4.
Kitano, H. (1990). Designing neural networks using genetic
algorithms with graph generation system. Complex
Systems, 4:461–476.
Komosinski, M. (2005). Framsticks: a platform for model-
ing, simulating and evolving 3D creatures, chapter 2,
page 37–66. Springer, New York, first edition.
Orkin, J. (2013). Collective Artificial Intelligence: Sim-
ulated Role-Playing from Crowdsourced Data. PhD
thesis, MIT.
Pajintov, A. (1984). Tetris. http://www.tetris.com. Ac-
cessed: 2015-06-15.
Pilat, M. L. (2009). Morphid Academy: A Virtual Labora-
tory for Evolution of Form and Function. PhD thesis,
University of Calgary.
Shen, H., Yosinski, J., Kormushev, P., Caldwell, D. G., and
Lipson, H. (2012). Learning fast quadruped robot
gaits with the rl power spline parameterization. Cy-
bernetics and Information Technologies, 12(3):66–75.
Sims, K. (1994). Evolved virtual creatures. In SIGGRAPH
’94: Proceedings of the 21st annual conference on
Computer graphics and interactive techniques.
Sims, K. (1997). Galapagos. http://karlsims.com/
galapagos/index.html. Accessed: 2015-01-01.
Sisnett, R. (2012). Parallel genetic algorithms on cluster ar-
chitecture: A case study. In Proceedings of the 2nd In-
ternational Super Computing Conference in Mexico.
Ventrella, J. (1999). Animated Artificial Life. Perseus
Books.
Zagal, J. and Alitzer, R. (2014). Examining rpg elements
systems of character progression. In Proceedings of
the 2014 Conference on the Foundations of Digital
Games.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
312
