Diffusion Bases Dimensionality Reduction
Alon Schclar
1
and Amir Averbuch
2
1
School of Computer Science, The Academic College of Tel-Aviv Yaffo, POB 8401, Tel Aviv, 61083, Israel
2
School of Computer Science, Tel Aviv University, POB 39040, Tel Aviv, 69978, Israel
Keywords:
Dimensionality Reduction, Unsupervised Learning.
Abstract:
The overflow of data is a critical contemporary challenge in many areas such as hyper-spectral sensing, infor-
mation retrieval, biotechnology, social media mining, classification etc. It is usually manifested by a high
dimensional representation of data observations. In most cases, the information that is inherent in high-
dimensional datasets is conveyed by a small number of parameters that correspond to the actual degrees of
freedom of the dataset. In order to efficiently process the dataset, one needs to derive these parameters by
embedding the dataset into a low-dimensional space. This process is commonly referred to as dimensionality
reduction or feature extraction. We present a novel algorithm for dimensionality reduction – diffusion bases –
which explores the connectivity among the coordinates of the data and is dual to the diffusion maps algorithm.
The algorithm reduces the dimensionality of the data while maintaining the coherency of the information that
is conveyed by the data.
1 INTRODUCTION
High dimensional datasets can be found in many ar-
eas such as information retrieval, biotechnology, so-
cial media, hyper-spectral sensing, classification etc.
These datasets are composed of observations that
were acquired by a set of sensors. The dimension of a
data observation is the number of values that describe
it. A simple example is an ordinary color image where
each pixel has 3 values that represent the red, green
and blue intensities. In this example, the dimension-
ality is low (equals to 3). In contrast, the dimension-
ality of hyper-spectral images may reach a few hun-
dreds or even thousands - according to the number of
wavelengths that describe the image.
The main problem of high dimensional data is the
so called curse of dimensionality, which means that
the complexity of many algorithms grows exponen-
tially with the increase of the dimensionality of the
input data. Commonly, the acquiring sensors produce
data whose dimensionality is much higher than the
actual degrees of freedom of the data. Unfortunately,
this phenomenon is usually unavoidable due to the in-
ability to produce a special sensor for each applica-
tion. This can be attributed to the lack of knowledge
which sensors are more important for the task at hand.
Consider, for example, a task that separates red ob-
jects from green objects using an off-the-shelf digital
camera. In this case, the camera will produce, in ad-
dition to the red and green channels, a blue channel,
which is unnecessary for this task.
In order to efficiently process high-dimensional
datasets, one must first analyze their geometrical
structure and detect the parameters that govern the
structure of the dataset. This number of parameters
is referred to as the intrinsic dimension (ID) of the
dataset and is equal to the degrees of freedom that are
inherent in the data. Thus, the information that is con-
veyed by the dataset can be described by a set of vec-
tors whose dimension is equal to the ID of the origi-
nal dataset. Dimensionality reduction algorithms con-
struct a mapping between high-dimensional datasets
and low-dimensional datasets whose dimension is
close, or ideally equal, to the ID of the original
datasets. The mapping should preserve the geometri-
cal structure of the high-dimensional dataset as much
as possible.
We propose a novel algorithm for the reduc-
tion of dimensionality which we call diffusion bases
(DB). The algorithm explored the non-linear variabil-
ity among the coordinates of the data and is dual to
the diffusion maps (DM) (Coifman and Lafon, 2006)
scheme. Both algorithms employ a manifold learn-
ing approach. However, depending on the size and
dimensionality of the dataset - the DB algorithm may
reduce the dimensionality at a computational cost that
Schclar, A. and Averbuch, A..
Diffusion Bases Dimensionality Reduction.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 3: NCTA, pages 151-156
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
151

is lower than that of the DM algorithm. The DM al-
gorithms has been successfully applied to the detec-
tion of moving vehicles (Schclar et al., 2010) and to
the construction of ensembles of classifiers (Schclar
et al., 2012).
This paper is organized as follows: in section 2 we
present a short survey of related work on dimension-
ality reduction. The diffusion maps scheme (Coifman
and Lafon, 2006) is briefly described in section 3. In
section 4 we introduce the Diffusion bases (DB) algo-
rithm. Concluding remarks are given in section 5.
2 RELATED WORKS
The theoretical foundations of dimensionality reduc-
tion were laid in the pioneering work by Johnson
and Lindenstrauss (Johnson and Lindenstrauss, 1984)
who showed that N points in N dimensional space can
almost always be projected to a space of dimension
C log N with control on the ratio of distances and the
error (distortion). Bourgain (Bourgain, 1985) showed
that any metric space with N points can be embed-
ded by a bi-Lipschitz map into an Euclidean space
of logN dimension with a bi-Lipschitz constant of
logN. Randomized versions of this theorem were
used for various applications such as protein map-
ping (Linial et al., 1997), reconstruction of frequency
sparse signals (Candes et al., 2006; Donoho, 2006)
and construction of ensembles of classifiers (Schclar
and Rokach, 2009)
The general problem of dimensionality reduction
has been extensively investigated. Classical tech-
niques for dimensionality reduction such as Principal
Component Analysis (PCA) and Multidimensional
Scaling (MDS), are simple to implement and can be
efficiently computed. However, PCA and classical
MDS can discover the true structure of data only
if it lies on or near a linear subspace of the high-
dimensional input space (Mardia et al., 1979). PCA
finds a low-dimensional embedding of the data points
that best preserves their variance as measured in the
high-dimensional input space. Classical MDS finds
an embedding that preserves the inter-point distances,
and is equivalent to PCA when these distances are
the Euclidean distances. However, the pitfall of these
methods is that they are global i.e. they take into ac-
count the distances between every pair of points. This
makes them susceptible to noise and outliers. Further-
more, many datasets contain nonlinear structures that
can not be detected by PCA and MDS.
Some dimensionality reduction methods amend
this pitfall by considering only the distances to the
closest neighboring points of each point. Two algo-
rithms in this category are Local Linear Embedding
(LLE) (Roweis and Saul, 2000) and ISOMAP (Tenen-
baum et al., 2000). The LLE algorithm attempts to
discover nonlinear structure in high dimensional data
by exploiting the local symmetries of linear recon-
structions. The ISOMAP (Tenenbaum et al., 2000)
approach uses classical MDS but seeks to preserve
the intrinsic geometry of the data as captured by the
geodesic manifold distances between all pairs of data
points. Another algorithm that falls into this cate-
gory is the Diffusion Maps (DM) (Coifman and Lafon,
2006) manifold learning scheme. This algorithm uses
the random walk distance metric which takes into ac-
count all the paths between every pair of points. This
distance reflects the connectivity among the points
and is more robust to noise. Furthermore, DM can
provide parametrization of the data when only the
point-wise similarity matrix is available. This may
occur either when there is no access to the original
data or when the original data consists of abstract ob-
jects.
3 DIFFUSION MAPS (DM)
This section briefly describes the DM (Coifman and
Lafon, 2006) algorithm. Given a set of data points
Γ =
{
x
i
}
m
i=1
, x
i
∈ R
n
(1)
the DM algorithm includes the following steps:
1. Construction of an undirected graph G on Γ (the
vertices correspond to the data points) with a
weight function w
ε
that corresponds to the local
point-wise similarity between the points in Γ
1
.
2. Derivation of a random walk on G via a Markov
transition matrix P that is obtained from w
ε
.
3. Eigen-decomposition of P.
By designing a local geometry that reflects quantities
of interest, it is possible to construct a diffusion oper-
ator whose eigen-decomposition enables the embed-
ding of Γ into a space Y of substantially lower dimen-
sion. The Euclidean distance between a pair of points
in the reduced space corrsponds to a diffusion met-
ric that measures the proximity of points in terms of
their connectivity in the original space. Specifically,
the Euclidean distance between a pair of points, in Y,
is equal to the random walk distance between the cor-
responding pair of points in the original space.
The eigenvalues and eigenfunctions of P define an
embedding of the data through the diffusion map.
1
G is sparse since only the points in the local neighbor-
hood of each point are considered. Wider neighborhood are
explored via a diffusion process. In case we are only given
w
ε
, this step is skipped.
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
152

3.1 Building the Graph G and the
Weight Function w
ε
Let Γ be a set of points in R
n
as defined in Eq. (1).
We construct the graph G(V,E),
|
V
|
= m, on Γ in
order to study the intrinsic geometry of this set. A
weight function w
ε
(x
i
,x
j
), which measures the pair-
wise similarity between the points, is introduced. For
all x
i
,x
j
∈ Γ, the weight function has the following
properties:
• symmetry: w
ε
(x
i
,x
j
) = w
ε
(x
j
,x
i
)
• non-negativity: w
ε
(x
i
,x
j
) ≥ 0
• fast decay: given a scale parameter ε >
0, w
ε
(x
i
,x
j
) → 0 when
x
i
− x
j
ε and
w
ε
(x
i
,x
j
) → 1 when
x
i
− x
j
ε. The sparsity
of G is a result of this property.
Note that the parameter ε defines a notion of neigh-
borhood. In this sense, w
ε
defines the local geome-
try of Γ by providing a first-order pairwise similar-
ity measure for ε-neighborhoods of every point x
i
.
Higher order similarities are derived through a diffu-
sion process. A common choice for w
ε
is the Gaus-
sian kernel w
ε
(x
i
,x
j
) = exp
−
k
x
i
−x
j
k
2
2ε
. However,
other weight functions can be used and the choice of
the weight function essentially depends on the appli-
cation at hand.
Successful dimensionality reduction which pre-
serves the geometry of the original dataset strongly
depends on the choice of ε. In the Appendix we dis-
cuss the choice of ε and rigorously define the range
from which ε should to be selected.
3.2 Construction of the Normalized
Graph Laplacian
The non-negativity property of w
ε
allows to normalize
it into a Markov transition matrix P where the states of
the corresponding Markov process are the data points.
This enables to analyze Γ via a random walk.
Formally, P = (p(x
i
,x
j
))
i, j=1,...,m
is constructed as
follows:
p(x
i
,x
j
) =
w
ε
(x
i
,x
j
)
d (x
i
)
(2)
where
d (x
i
) =
m
∑
j=1
w
ε
(x
i
,x
j
) (3)
is the degree of x
i
. If we let D = (d
i j
) be a m × m di-
agonal matrix where d
ii
= d (x
i
), and we let W
ε
be the
weight matrix that corresponds to the weight function
w
ε
, P can be derived by
P = D
−1
W
ε
. (4)
P is a Markov matrix since the sum of each row in P is
1 and p (x
i
,x
j
) ≥ 0. Thus, p(x
i
,x
j
) can be viewed as
the probability to move from x
i
to x
j
in a single time
step. By raising P to the power t, this probability is
propagated to nodes in the neighborhood of x
i
and x
j
and the result is the probability for this move in t time
steps. We denote this probability by p
t
(x
i
,x
j
). These
probabilities measure the connectivity of the points
within the graph. The parameter t controls the scale
of the neighborhood in addition to the scale which is
provided by ε.
3.3 Eigen-decomposition
The close relation between the asymptotic behavior
of P, i.e. the properties of its eigen-decomposition
and the clusters that are inherent in the data, was ex-
plored in (Chung, 1997; Fowlkes et al., 2004). We
denote the left and the right bi-orthogonal eigenvec-
tors of P by
{
µ
k
}
k=1,...,m
and
{
ν
k
}
k=1,...,m
, respec-
tively. Let
{
λ
k
}
k=1,...,m
be the eigenvalues of P where
|
λ
1
|
≥
|
λ
2
|
≥ ... ≥
|
λ
m
|
.
It is well known that lim
t→∞
p
t
(x
i
,x
j
) = µ
1
(x
j
).
Coifman et al. (Coifman et al., 2005) show that for
finite time t we have
p
t
(x
i
,x
j
) =
m
∑
k=1
λ
t
k
ν
k
(x
i
)µ
k
(x
j
). (5)
A fast decay of
{
λ
k
}
is achieved by an appropriate
choice of ε. Thus, to achieve a relative accuracy δ > 0,
only a few terms η (δ) are required in the sum in Eq.
(5).
Coifman and Lafon (Coifman and Lafon, 2006)
introduced the diffusion distance
D
2
t
(x
i
,x
j
) =
m
∑
k=1
(p
t
(x
i
,x
k
) − p
t
(x
k
,x
j
))
2
µ
1
(x
k
)
.
This formulation is derived from the known ran-
dom walk distance in Potential Theory: D
2
t
(x
i
,x
j
) =
p
t
(x
i
,x
i
) + p
t
(x
j
,x
j
) − 2p
t
(x
i
,x
j
) where the factor 2
is due to the fact that G is undirected.
Averaging along all the paths from x
i
to x
j
results
in a distance measure that is more robust to noise and
topological short-circuits than the geodesic distance
(Tenenbaum et al., 2000). Finally, the diffusion dis-
tance can be expressed in terms of the right eigenvec-
tors of P (see (Keller and Coifman, 2006) for a proof):
D
2
t
(x
i
,x
j
) =
m
∑
k=1
λ
2t
k
(ν
k
(x
i
) − ν
k
(x
j
))
2
.
Diffusion Bases Dimensionality Reduction
153

It follows that in order to compute the diffusion dis-
tance, one can simply use the right eigenvectors of P.
Moreover, this facilitates the embedding of the origi-
nal points in a Euclidean space R
η(δ)−1
by:
Ξ
t
: x
i
→
λ
t
2
ν
2
(x
i
),λ
t
3
ν
3
(x
i
),. .., λ
t
η(δ)
ν
η(δ)
(x
i
)
.
The first eigenvector ν
1
is not used since it is con-
stant. This also endows coordinates on the set Γ. Es-
sentially, η(δ) n due to the fast decay of the eigen-
values of P. Furthermore, η(δ) depends only on the
primary intrinsic variability of the data as captured by
the random walk and not on the original dimension-
ality of the data. This data-driven method enables the
parametrization of any set of points - abstract or not
- provided the similarity matrix w
ε
of the points is
available.
4 DIFFUSION BASES (DB)
Diffusion bases (DB) is a dual algorithm to the DM
algorithm in the sense that it explores the connectiv-
ity among the coordinates of the original data instead
of the connectivity among the data points. Both algo-
rithms share a graph Laplacian construction, however,
the DB algorithm uses the Laplacian eigenvectors as
an orthonormal system and projects the original data
on it.
Let Γ =
{
x
i
}
m
i=1
, x
i
∈ R
n
, be the original dataset
as defined in Eq. (1) and let x
i
( j) denote the j-th
coordinate of x
i
, 1 ≤ j ≤ n. We define the vector x
0
j
,
(x
1
( j), ... ,x
m
( j)) to be the j-th coordinate of all the
points in Γ. We construct the set
Γ
0
=
x
0
j
n
j=1
. (6)
The DM algorithm is applied to the set Γ
0
. The
right eigenvectors of P constitute an orthonormal ba-
sis
{
ν
k
}
k=1,...,n
, ν
k
∈ R
n
. This bares some similarity
to PCA, however, the diffusion process has the poten-
tial to achieve better dimensionality reduction due to:
(a) its ability to capture non-linear manifolds within
the data by local exploration of each coordinate; (b)
its robustness to noise. Furthermore, this process is
more general than PCA and it produces similar results
to PCA when the weight function w
ε
is linear e.g. the
inner product, Euclidean distance.
Next, we use the eigenvalue decay property of
the eigen-decomposition to extract only the first η(δ)
eigenvectors B ,
{
ν
k
}
k=1,...,η(δ)
(we do not exclude
the first eigenvector as mentioned in section 3.3).
We project the original data Γ onto the basis B.
Let Γ
B
be the set of these projections which is de-
fined as follows: Γ
B
=
{
g
i
}
m
i=1
, g
i
∈ R
η(δ)
, where
g
i
=
x
i
· ν
1
,.. .,x
i
· ν
η(δ)
, i = 1, ... ,m and · denotes
the inner product operator. Γ
B
contains the coordi-
nates of the original points in the orthonormal system
whose axes are given by B. Alternatively, Γ
B
can be
interpreted in the following way: the coordinates of g
i
contain the correlation between x
i
and the directions
given by the vectors in B. A summary of the Diffu-
sionBases procedure is given in Algorithm 1.
The duality connection between the DB and DM
algorithms can be demonstrated, for example, when
the weight function is defined by the dot prod-
uct, i.e. w(x
i
,x
j
) =
x
i
,x
j
. In this case DM
and DB are connected through the singular value
decomposition of the weight matrix W = BSR
T
.
Namely, WW
T
= BSR
T
RSB
T
= BS
2
B
T
and W
T
W =
RSB
T
BSR
T
= RD
2
R
T
and thus the results of the
eigen-decomposition steps in the DM and DB algo-
rithms are given by B and R, respectively.
Algorithm 1: The Diffusion Bases Algorithm.
DiffusionBases(Γ
0
, w
ε
, ε, δ)
1. Calculate the weight function w
ε
x
0
i
,x
0
j
, i, j =
1,.. .n.
2. Construct a Markov transition matrix P by nor-
malizing the sum of each row in w
ε
to be 1:
p
x
0
i
,x
0
j
=
w
ε
x
0
i
,x
0
j
d (x
0
i
)
where d (x
0
i
) =
∑
n
j=1
w
ε
x
0
i
,x
0
j
.
3. Perform eigen-decomposition of p
x
0
i
,x
0
j
p
x
0
i
,x
0
j
≡
n
∑
k=1
λ
k
ν
k
x
0
i
µ
k
x
0
j
where the left and the right eigenvectors of P are
given by
{
µ
k
}
and
{
ν
k
}
, respectively, and
{
λ
k
}
are the eigenvalues of P in descending order of
magnitude.
4. Project the original data Γ onto the orthonormal
system B ,
{
ν
k
}
k=1,...,η(δ)
:
Γ
B
=
{
g
i
}
m
i=1
, g
i
∈ R
η(δ)
where
g
i
=
x
i
· ν
1
,.. .,x
i
· ν
η(δ)
,
i = 1, ... ,m, ν
k
∈ B, 1 ≤ k ≤ η (δ)
and · is the inner product.
5. return Γ
B
.
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
154

5 FUTURE RESEARCH
It was shown in (Coifman and Lafon, 2006) that any
positive semi-definite kernel may be used for the di-
mensionality reduction. Rigorous analysis of families
of kernels to facilitate the derivation of an optimal ker-
nel for a given set Γ is an open problem.
The parameter η (δ) determines the dimensional-
ity of the diffusion space. A rigorous method for
choosing η(δ) will facilitate an automatic embedding
of the data. Naturally, η (δ) is data driven (similarly
to ε) i.e. it depends on the set Γ at hand.
Finally, various applications of the diffusion bases
scheme are currently being investigated by the authors
- namely, video segmentation and construction of en-
sembles of classifiers.
REFERENCES
Bourgain, J. (1985). On lipschitz embedding of finite metric
spaces in hilbert space. Israel Journal of Mathematics,
52:46–52.
Candes, E., Romberg, J., and Tao, T. (2006). Robust
uncertainty principles: Exact signal reconstruction
from highly incomplete frequency information. IEEE
Transactions on Information Theory, 52(2):489–509.
Chung, F. R. K. (1997). Spectral Graph Theory. AMS
Regional Conference Series in Mathematics, 92.
Coifman, R. R. and Lafon, S. (2006). Diffusion maps. Ap-
plied and Computational Harmonic Analysis: special
issue on Diffusion Maps and Wavelets, 21:5–30.
Coifman, R. R., Lafon, S., Lee, A., Maggioni, M., Nadler,
B., Warner, F., and Zucker, S. (2005). Geometric dif-
fusions as a tool for harmonics analysis and structure
definition of data: Diffusion maps. In Proceedings of
the National Academy of Sciences, volume 102, pages
7432–7437.
Donoho, D. (2006). Compressed sensing. IEEE Transac-
tions on Information Theory, 52(4):1289–1306.
Fowlkes, C., Belongie, S., Chung, F., and Malik, J. (2004).
Spectral grouping using the nystr
¨
om method. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 26(2):214–225.
Hein, M. and Audibert, Y. (2005). Intrinsic dimensional-
ity estimation of submanifolds in euclidean space. In
Proceedings of the 22nd International Conference on
Machine Learning, pages 289–296.
Johnson, W. B. and Lindenstrauss, J. (1984). Extensions
of lipshitz mapping into hilbert space. Contemporary
Mathematics, 26:189–206.
Keller, S. L. Y. and Coifman, R. R. (2006). Data fusion
and multi-cue data matching by diffusion maps. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 28(11):1784–1797.
Linial, M., Linial, N., Tishby, N., and Yona, G. (1997).
Global self-organization of all known protein se-
quences reveals inherent biological signatures. Jour-
nal of Molecular Biology, 268(2):539–556.
Mardia, K. V., Kent, J. T., and Bibby, J. M. (1979). Multi-
variate Analysis. Academic Press, London.
Roweis, S. T. and Saul, L. K. (2000). Nonlinear dimension-
ality reduction by locally linear embedding. Science,
290:2323–2326.
Schclar, A., Averbuch, A., Hochman, K., Rabin, N., and
Zheludev, V. (2010). A diffusion framework for de-
tection of moving vehicles. Digital Signal Process-
ing,, 20(1):111–122.
Schclar, A. and Rokach, L. (ICEIS 2009). Random projec-
tion ensemble classifiers. Lecture Notes in Business
Information Processing, Proceedings of the 11th Con-
ference on Enterprise Information System.
Schclar, A., Rokach, L., and Amit, A. (2012). Diffusion
ensemble classifiers. In Proceedings of the 4th Inter-
national Conference on Neural Computation Theory
and Applications (NCTA 2012), Barcelona, Spain.
Tenenbaum, J. B., de Silva, V., and Langford, J. C. (2000).
A global geometric framework for nonlinear dimen-
sionality reduction. Science, 290:2319–2323.
APPENDIX: CHOOSING ε
The choice of ε is critical to achieve the optimal per-
formance of the DM and DB algorithms since it de-
fines the size of the local neighborhood of each point.
On one hand, a large ε produces a coarse analysis
of the data as the neighborhood of each point will
contain a large number of points. In this case, the
similarity weight will be close to one for most pairs
of points. On the other hand, a small ε might pro-
duce neighborhoods that contain only one point. In
this case, the similarity will be zero for most pairs of
points. Clearly, an adequate choice of ε lies between
these two extreme cases and should be derived from
the data.
In the following, we derive the range from which ε
should be chosen when a Gaussian weight function is
used and when the dataset Γ approximately lies near a
low dimensional manifold. We denote by d the intrin-
sic dimension of M. Let L = I − P = I − D
−1
W be the
normalized graph Laplacian (Chung, 1997) where P
was defined in Eq. (4) and I is the identity matrix.
The matrices L and P share the same eigenvectors.
Furthermore, Singer (2006) proved that if the points
in Γ are independently uniformly distributed over M
then with high probability
1
ε
m
∑
j=1
L
i j
f (x
j
) =
1
2
4
M
f (x
i
) + O
1
m
1/2
ε
1/2+d/4
,ε
(7)
where f : M → R is a smooth function and 4
M
is the
continuous Laplace-Beltrami operator of the manifold
Diffusion Bases Dimensionality Reduction
155
M. The error term is composed of a variance term
O
1
m
1/2
ε
1/2+d/4
, which is minimized by a large value
of ε, and a bias term O (ε), which is minimized by a
small value of ε.
We utilize the scheme that was proposed in (Hein
and Audibert, 2005) and examine the sum of the
weight matrix elements
S
ε
=
m
∑
i=1
m
∑
j=1
w
ε
(x
i
,x
j
) =
m
∑
i=1
m
∑
j=1
exp
−
x
i
− x
j
2
2ε
!
(8)
as a function of ε. Let Vol (M) be the volume of the
manifold M. The sum in Eq. (8) can be approximated
by its mean value integral
S
ε
≈
m
2
Vol
2
(M)
Z
M
Z
M
exp
−
k
x − x
0
k
2
2ε
!
dxdx
0
(9)
provided the variance term in Eq. (7) is sufficiently
small.
Moreover, we use the fact that for small values of
ε the manifold locally looks like its tangent space R
d
and thus
Z
M
exp
−
k
x − x
0
k
2
2ε
!
dx ≈
Z
R
d
exp
−
k
x − x
0
k
2
2ε
!
dx = (2πε)
d/2
. (10)
Combining Eqs. (8)-(10), we get
S
ε
≈
m
2
Vol (M)
(2πε)
d/2
.
Applying logarithm on both sides yields
log(S
ε
) ≈
d
2
log(ε) + log
m
2
(2π)
d/2
Vol (M)
!
.
Consequently, the slope of S
ε
as a function of ε on a
log-log scale is
d
2
. However, this slope is only linear
in a limited subrange of ε since lim
ε→∞
S
ε
= m
2
and
lim
ε→0
S
ε
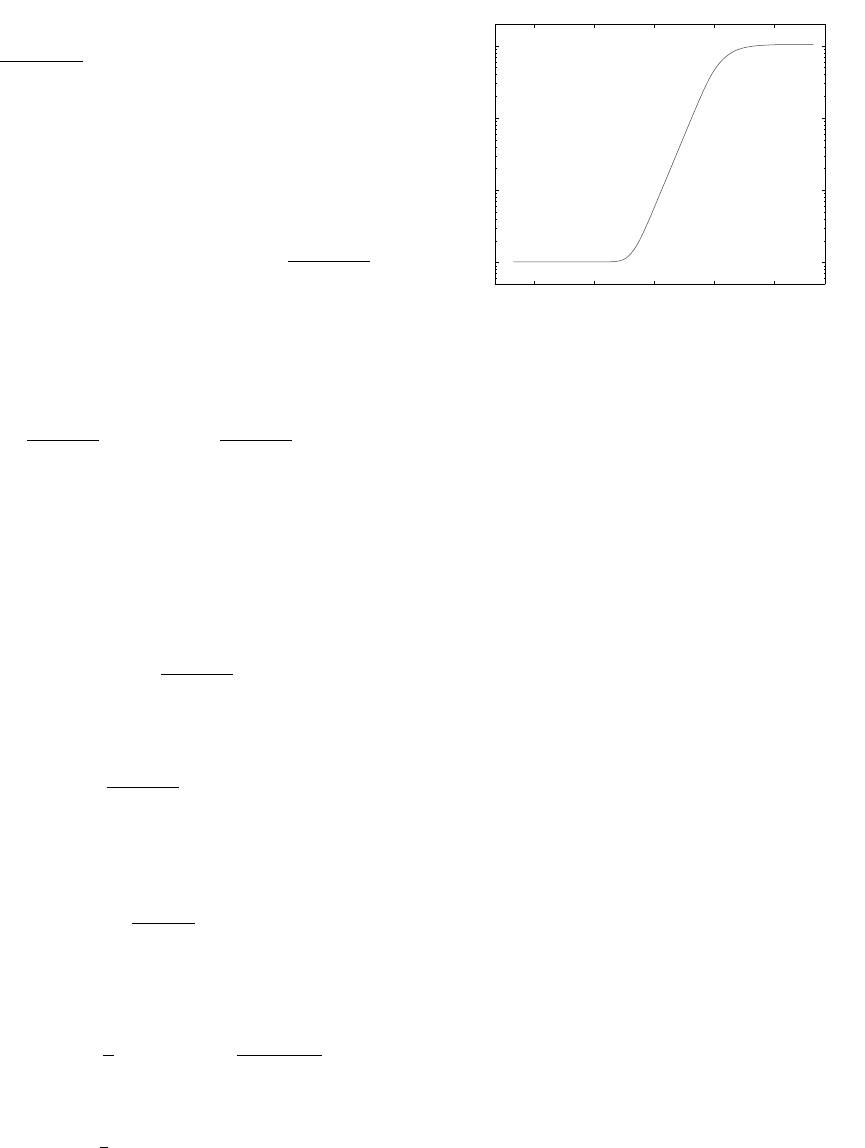
= m as illustrated in Fig. 1. In this sub-
range, the error terms in Eq. (7) are smaller than they
are in the rest of the ε range. Thus, an adequate ε
should be chosen from this linear subrange.
10
−4
10
−2
10
0
10
2
10
4
10
3
10
4
10
5
10
6
log(ε)
log(S
ε
)
Figure 1: A plot of S
ε
as a function of ε on a log-log scale.
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
156
