Two Body Dynamic Model for Speed Skating Driven by the Skaters

Leg Extension

E. van der Kruk, H. E. J. Veeger, F. C. T. van der Helm and A. L. Schwab

Department of Biomechanical Engineering, Delft University of Technology, Mekelweg 2, Delft, The Netherlands

Keywords: Speed Skating, Multi-Body Dynamics, Mathematical Model, Verification.

1 OBJECTIVES

In speed skating forces are generated by pushing in a

sideward direction against an environment, which

moves relative to the skater. De Koning et al. (1987)

showed that there is a distinct difference in the

coordination pattern between (elite) speed skaters.

Models can help to give insight in this peculiar

technique and ideally find an optimal motion pattern

for each individual speed skater. Currently there are

three models describing and optimizing the

behaviour and performance of skaters, of which only

two are relevant in terms of coordination patterns

(Allinger and Bogert 1997; Otten 2003). However,

none of them have been shown to accurately predict

the observed coordination pattern via verification

with empirical kinetic and kinematic data.

Therefore, the objectives of this study are to present

a verified three dimensional inverse skater model

with minimal complexity, based on the idea of

(Cabrera et al. 2006), modelling the speed skating

motion on the straights. The model is driven by the

changing distance between the torso and the skate

(further referred to as the leg extension), which is

also the true input of the skater to generate a global

motion. This input, which is indirectly also a

measure of the knee extension of the skater, is a

variable familiar to the speed skaters and coaches. In

this extended abstract we verify this novel model for

two strokes (left and right) of one skater through

correlation with observed kinematics and forces.

2 METHODS

2.1 Model Description

The model presented in this section simulates the

upper body transverse translation of the skater

together with the forces exerted by the skates on the

ice. The model input is the measured leg extension

(coordination pattern). Based on empirical data from

previous studies using elite skaters, the double

stance phase, the time in which both skates are in

contact with the ice, is rather short. For the sake of

simplicity, we assume that there is only one skate at

a time in contact with the ice, alternating left and

right. The point of alternation is defined as the

moment in time where the forces exerted on both

skates are equal. Furthermore the arm movements

and the rotations of the upper body are assumed to

be of marginal effect on the overall power and are

therefore neglected. Based on these assumptions, the

skater can be considered as a combination of two

point masses, which are situated at the upper body

(mass B) and at each (active) skate (mass S). The

body mass of the skater is distributed over the two

active masses by a constant mass distribution

coefficient (η) to compensate for the shift in the

center of mass position during the speed skating

movement. Each mass has three degrees of freedom.

The set of parameters is restricted to the position

coordinates of mass B (

bbb

), two translations

in the transverse plane of mass S with the position

coordinates (

) (because the skate is assumed

to be on the ice, making z

=0 at all times) and one

rotation in the same plane, the steer angle (φ

). The

orientation of the skate is of importance for the

constraint forces acting on the skate. All other

rotations of the skates are ignored.

Since we want to obtain a model which is driven

by generalized (local) coordinates, we introduce a

set of generalized coordinates

q (Figure 2), so the

global coordinates can be expressed in terms of leg

Kruk, E., Veeger, H., Helm, F. and Schwab, A..

Two Body Dynamic Model for Speed Skating Driven by the Skaters Leg Extension.

extension via the kinematic relation

()

xfq=

These generalized coordinates consist of the leg

extension (

,,,

ssss

wuv

)(Figure 2), that is actively

controlled by the skater and therefore serves as the

input coordinates to the model and the generalized

coordinates of the upper body (

), which will

be a result of the system dynamics (equal to

)

The equations of motion are expressed in

generalized coordinates, so that the constraints are

inherently fulfilled. Since we assume no lateral slip,

a non-holonomic constraint acting in the lateral

direction of the skate was added, causing the

undetermined external force λ perpendicular to the

skate blade in the transverse plane. This leaves a

model with two degrees of freedom in position and

only one in velocity. The known external forces

acting on the model are the air frictional forces and

the ice frictional forces.

2.2 Solving the Model

The model is solved in two steps. First, since the

parameters (

,,,

ssss

wuv

) are considered inputs

and the air frictional forces acting on the upper body

are assumed to be known, the constraint force λ and

the transverse position of the upper body (

)

can be determined by means of integration (Runge

Kutta method), starting from the initial condition

()

,0 ,0 ,0 ,0

,,,

bbbb

xyxy



. The constraint is fulfilled for

each integration step by a projection method. Hereby

a minimization problem was formulated, concerning

the distance from the predicted solution to the

solution which is on the constraint surface. The

global coordinates

, which are the global

positions of the upper body and the skate, can then

be found analytically via the kinematic relation.

Finally, with the found upper body position and

the local forces acting on the skate can be solved

analytically such that a complete two-body dynamic

model of the skater has been established.

2.3 Model Verification

The purpose of the model verification is to quantify

the error between the simulated data and the

measured forces and positions. The forces were

measured by a set of instrumented klapskates (van

der Kruk et al. 2015). The position of the masses

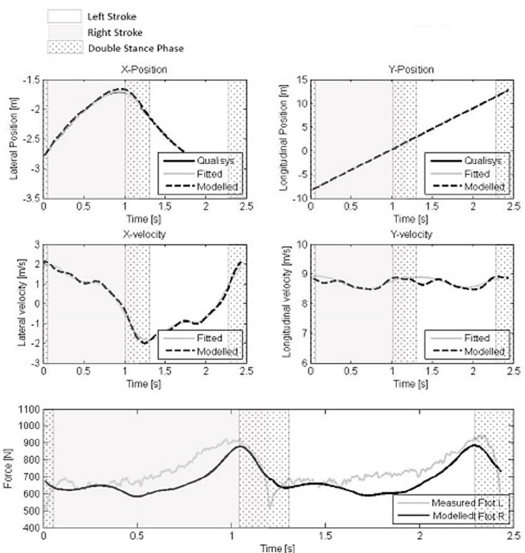
Figure 1: The fitted data of two consecutive strokes for position and velocity of mass B and the total force. The grey area

indicates a left stroke, the white area a right stroke, the pattern indicates the double stance phase as measured.. Y is in line

with the skate lane, X is perpendicular to the skate lane.

Table 1: Error between the simulated data and the measured data.

RMSE Mean Error SD Error Jmin

x-position 0.025 [m] 0.019 [m] 0.016 [m] 0.000310

y-position 0.045 [m] 0.033 [m] 0.031 [m] 0.000004

x-velocity 0.116 [m/s] 0.002 [m/s] 0.117 [m/s] 0.0028

y-velocity 0.096 [m/s] -0.048 [m/s] 0.084 [m/s] 0.000123

F 82 [N] -54.0 [N] 61.8 [N] 0.0305

Figure 2: The global and generalized coordinates of the

two-mass skater model. Leg extension consists of vertical

distance (w

) and horizontal distance between the mass S

and mass B in heading direction (u

) and perpendicular to

heading direction (v

) and the heading of the skate (θ

)

(orientation).

was measured by a motion capture system on 50

meter of the straight part of the rink, with a passive

marker on the Lateral Malleolus (representing mass

S) and on the back near the Sacrum (representing

mass B). A parametric function was fitted to the

recorded data, consisting of a linear and a geometric

function, which could be differentiated twice in

order to obtain velocity and acceleration data. The

air and ice friction were estimated based on previous

papers (van Ingen Schenau 1982; De Koning et al.

1992). The body mass was assumed to be distributed

equally over mass S and mass B. In this abstract the

data of one Dutch elite female speed skater are

presented (65kg, 1.75m).

3 RESULTS

The results show that the model estimated the

forward position and velocity of mass B the best

(Jmin (based on (Cabrera et al. 2006))), followed by

the lateral position and velocity, which were all

within 1% accuracy. The model was least accurate

for the force determination (Table 1). The forces

were consistently estimated too low (Figure 2,

bottom graph).

4 DISCUSSION

4.1 Kinematic Complexity

Preliminary results presented in this abstract showed

that the model, despite the simplicity, was able to

simulate the upper body movement accurately. The

forces on the skate were underestimated, which can

be explained by the simplicity of the model. The

skater was considered as a combination of two point

masses, which moreover were situated at fixed

positions on the body parts, with each a mass half of

the total body weight. In reality there might however

be a different mass distribution and the CoM of

these bodies move throughout the movement.

Additionally, the changing distance between the two

masses (leg extension), was modelled piston-like

without any damping. Optimization of the mass

distribution and determination of the true CoM (with

a full body marker set) will improve the model

estimation. The model would also benefit from

improved acceleration measurements by adding

IMU’s.

Although the double stance phase was neglected

based on previous papers, the collected data showed

that the double stance phase is apparent in about

13% of the stroke. However the force on the inactive

skate is low during this phase and the results do not

seem influenced by this assumption.

4.2 Frictional Forces

The estimation of air and ice friction based on

previous papers, probably caused an inaccuracy in

the model outcome. Moreover, the air friction was

assumed to be only dependent on velocity, while the

friction coefficient might differ within a stroke, due

to change of frontal area and drag. It would be

interesting to determine the magnitude and

repeatability of this change, in order to relate this to

the model error, and to perhaps improve the

estimation of the fluctuating character in the forward

velocity within one stroke.

4.3 Application

When the model is verified with more data, it will be

possible to determine the sensitivity of the model for

each parameter, and with that determine the

performance-dependent variables in speed skating.

This insight will help to provide more valuable

feedback on technique to skaters and coaches and

via optimization propose individual optimal

coordination patterns.

REFERENCES

Allinger, T.L. & Bogert, A.J., 1997. Skating technique for

the straights based on the optimization of a simulation

study. Medicine and Science in Sports and Exercise,

29, pp.279–286.

Cabrera, D., Ruina, A. & Kleshnev, V., 2006. A simple 1+

dimensional model of rowing mimics observed forces

and motions. Human Movement Science, 25(2),

pp.192–220.

Van Ingen Schenau, G.J., 1982. The influence of air

friction in speed skating. Journal of Biomechanics,

15(6), pp.449–458.

De Koning, J.J. et al., 1987. Push-Off Force in Speed

Skating. , pp.103–109.

De Koning, J.J., De Groot, G. & Van Ingen Schenau, G.J.,

1992. Ice friction during speed skating. Journal of

Biomechanics, 25(6), pp.565–571.

Van der Kruk, E. et al., (submitted) 2015. wireless

instrumented klapskates for speed skating,submitted

Otten, E., 2003. Inverse and forward dynamics: models of

multi-body systems. Phil. Trans. R. Soc. Lond.,

pp.1493–1500.