A Continuum among Logarithmic, Linear, and Exponential Functions,
and Its Potential to Improve Generalization in Neural Networks
Luke B. Godfrey and Michael S. Gashler
Department of Computer Science and Computer Engineering,
University of Arkansas, Fayetteville, AR, U.S.A.
Keywords:
Neural Networks, Activation Function.
Abstract:
We present the soft exponential activation function for artificial neural networks that continuously interpolates
between logarithmic, linear, and exponential functions. This activation function is simple, differentiable, and
parameterized so that it can be trained as the rest of the network is trained. We hypothesize that soft exponential
has the potential to improve neural network learning, as it can exactly calculate many natural operations that
typical neural networks can only approximate, including addition, multiplication, inner product, distance, and
sinusoids.
1 INTRODUCTION
Each neuron in an artificial neural network applies
a non-linear activation function to a weighted sum
of its inputs. The activation function serves the im-
portant role of enabling the neural network to fit to
non-linear curves and surfaces. If omitted, even deep
multi-layered neural networks reduce to be function-
ally equivalent to simple linear regression. Hence, the
activation function endowsthe neural network with its
representational power.
One might ask, which activation function is best
for neural networks? For years, the logistic and tanh
functions have been popular choices (Kalman and
Kwasny, 1992). More recently, rectified linear units
have been shown to possess desirable properties (Nair
and Hinton, 2010; Zeiler et al., 2013). While these
functions perform well empirically, little theoretical
basis has been found to justify their extensive use over
many other potential functions. We present the soft
exponential function, a novel activation function with
many desirable theoretical properties. It continuously
interpolates between logarithmic, linear, and expo-
nential activation functions. It enables neural net-
works to exactly compute many natural mathemati-
cal structures that can only be approximated by neural
networks that use traditional activation functions, in-
cluding addition, multiplication, exponentiation, dot
product, Euclidean and L-norm distance, Gaussian ra-
dial basis functions, and Fourier neural networks.
The next section derives soft exponential and the
remainder of the paper discusses its desirable proper-
ties.
2 DERIVATION
It is well known that multiplication can be imple-
mented by means of addition in logarithmic space.
That is,
p∗ q = e
(log
e
p)+(log
e
q)
. (1)
This property can enable neural networks that use
a mixture of logarithmic, linear, and exponential ac-
tivation functions to exactly perform the basic math-
ematical operation of multiplication. However, using
a mixture of different activation functions in a single
neural network adds a significant component of com-
plexity. Specifically, it leaves the user to determine
which activation function should be used with each
neuron in the network. If a function can be found that
continuously generalizes between logarithmic, linear,
and exponential functions, then a neural network with
a single activation function would be empowered to
autonomously learn to add, multiply, exponentiate,
and compute the logarithms as needed to accomplish
arbitrary tasks. Because these mathematical opera-
tions have proven to have significant value in nearly
all other areas of science, it is natural to suppose that
neural networks should be given the ability to per-
form the same operations when they attempt to au-
tonomously model various phenomena.
Godfrey, L. and Gashler, M..
A Continuum among Logarithmic, Linear, and Exponential Functions, and Its Potential to Improve Generalization in Neural Networks.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 1: KDIR, pages 481-486
ISBN: 978-989-758-158-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
481

A simple equation that continuously interpolates
between linear and exponential functions is
g(α, x) =
e
αx
− 1
α
+ α. (2)
Note that lim
α→0
g(α, x) = x, and g(1, x) = e
x
.
This function does not become a logarithmic function
(i.e. when α = −1), so it does not provide a complete
solution to our objective. However, we can invert g
with respect to x to obtain a function that interpolates
between logarithmic and linear functions:
g
−1
(α, x) =
log
e
(1+ α(x− α))
α
. (3)
Since g and g
−1
are equivalent when α = 0, we
can mathematically piece them together along that
edge without breaking continuity. We negate α in the
case of the inverse function and obtain the following
continuous piecewise function:
f(α, x) =
−
log
e
(1−α(x+α))
α
for α < 0
x for α = 0
e
αx
−1
α
+ α for α > 0.
(4)
Equation 4 interpolates between logarithmic, lin-
ear, and exponential functions. Although it is spliced
together, it is continuous both with respect to α and
with respect to x, and has a number of properties that
render it particularly useful as a neural network acti-
vation function. We call f the soft exponential activa-
tion function.
We can now address the challenge of creating a
continuum of operations between addition and multi-
plication. By substituting f into Equation 1, we ob-
tain a continuous generalization between these two
operations:
h(β, p, q) = f (β, f(−β, p) + f(−β, q)). (5)
If β = 0, this function adds p and q. If β = 1, it
multiplies p and q. Figure 1 illustrates this continuum
between addition and multiplication with the arbitrary
values p = 3 and q = 7. At β = 0, it correctly calcu-
lates 3 + 7 = 10, and at β = 1, it correctly calculates
3∗ 7 = 21.
3 ANALYSIS
Some of the nice properties of soft exponential in-
clude:
• f(−1, x) = log
e
(x)
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
h
(
β
3,7)
,
β
Figure 1: A plot of h(β, 3, 7). When β = 0, it correctly
calculates 3+ 7 = 10. When β = 1, it correctly calculates
3∗ 7 = 21.
• f(0, x) = x
• f(1, x) = e
x
• For other values of α, f(α, x) does something con-
tinuous and reasonable.
• The equation is simple, and can be implemented
in code with very few operations.
• It appears reasonably smooth when plotted. (See
Figures 2 and 3.)
• Negating α inverts the function, such that
f
−1
(α, x) = f(−α, x).
• For any constant value of α, f(α, x) is monotonic.
• It is continuously differentiable with respect to x,
∂f
∂x
=
(
1
1−α(α+x)
for α < 0
e
αx
for α ≥ 0
(6)
because
lim
α→0
+
∂f
∂x
≡ lim
α→0
−
∂f
∂x
≡ 1.
• And it is continuously differentiable with respect
to α,
∂f
∂α
=
log
e
(1−(α
2
+αx))−
2α
2
+αx
α
2
+αx−1
α
2
for α < 0
x
2
2
+ 1 for α = 0
α
2
+(αx−1)e
αx
+1
α
2
for α > 0
(7)
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
482
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
x
f
(
α
)
,
x
x
f
(1,
)=
e
x
x
f
(-1,
)=log ( )
e
x
x
f
(0,
)=
x
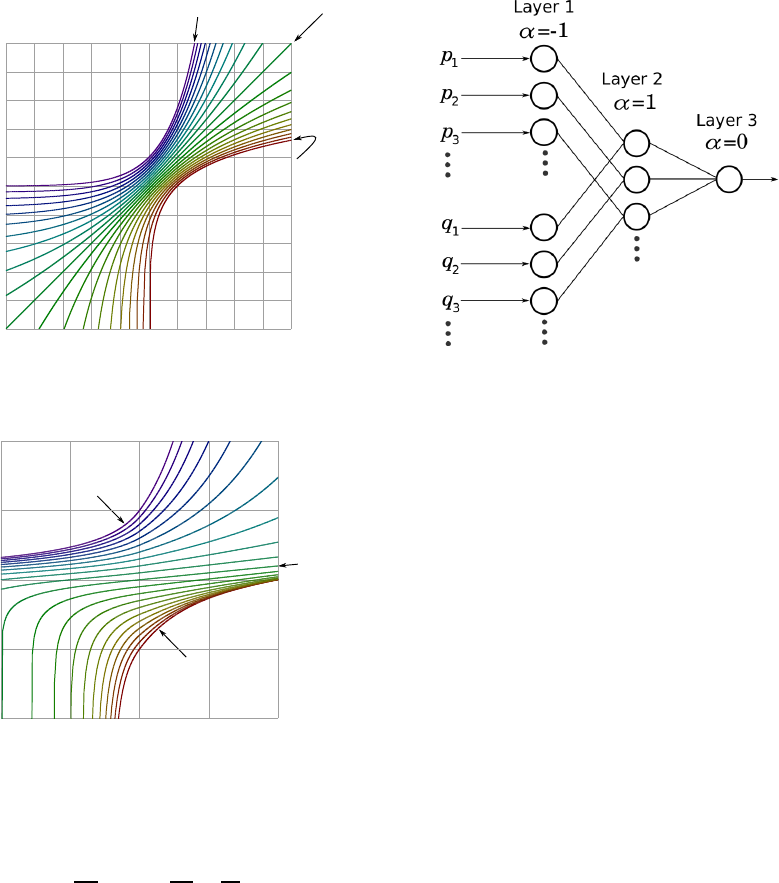
Figure 2: A plot of f(α, x) for α =
{−1, −0.9, −0.8,··· , 0.8, 0.9, 1.0} from red to purple.
-0.5
x
f
(
α
)
,
α
f
( ,
-5)
α
f
( ,
5)
α
f
( ,
0)
α
-1
0
0.5
1
-10
-5
0
5
10
Figure 3: A plot of f(α, x) for x =
{−5, −4.5, −4, ··· , 4, 4.5, 5} from red to purple.
because
lim
α→0
+
∂f
∂α
≡ lim
α→0
−
∂f
∂α
≡
x
2
2
+ 1.
• Because it is differentiable, it is possible to train
a neural network with soft exponential using gra-
dient descent. The alpha parameter of the activa-
tion function is updated in the same manner as the
weights, by stepping in the gradient direction that
reduces some objective function.
4 INNER PRODUCT
Another operation we might want to generalize is in-
ner product. The inner product is typically imple-
mented as, p · q = p
0
q
0
+ p
1
q
1
+ p
2
q
2
+ . . .. Inner
p
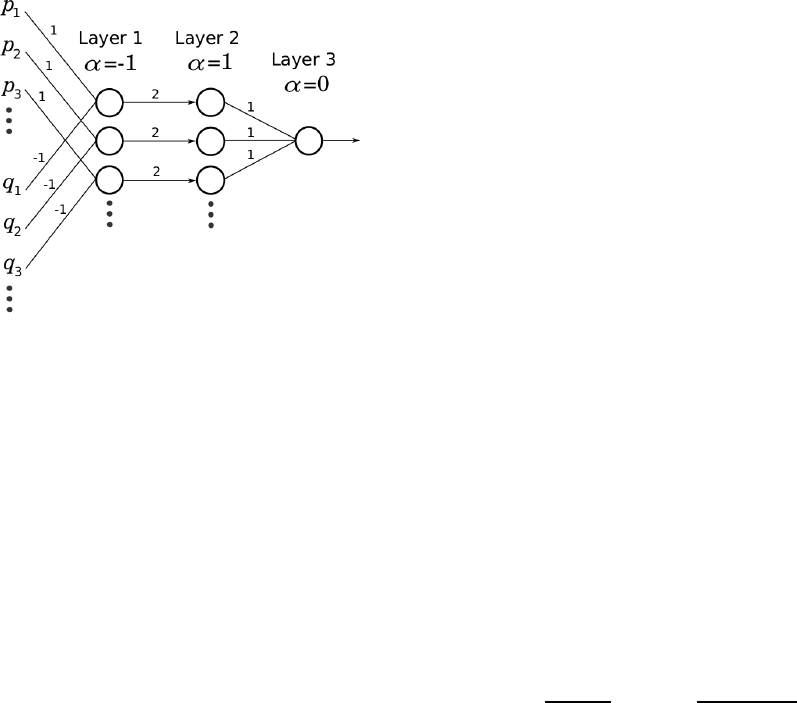
3
Figure 4: A neural network implementation of inner product
using soft exponential as an activation function. All of the
weights represented with lines in this figure have a value of
1. All other weights have a value of 0.
product could be implemented using a 3-layer neural
network as depicted in Figure 4. This network uses
soft exponential for the activation function in each of
its units. The first layer computes the logarithm of all
the elements in p and q. (All the units in this layer use
α = −1.) The second layer adds corresponding ele-
ments of p and q, and exponentiates the result. (All
the units in this layer use α = 1.) The third layer sums
all the pair-wise products together. (The unit in this
layer uses α = 0.)
One possible use for this generalization of inner
product is to implement a neural network version
of matrix factorization, a useful algorithm for rec-
ommender systems (Koren et al., 2009) and missing
value imputation for sparse matrix completion (Cai
et al., 2010). Matrix factorization has also proved to
be effective for document clustering (Xu et al., 2003),
text mining and spectral data analysis (Berry et al.,
2007), and molecular pattern discovery (Brunet et al.,
2004). A neural network with our activation function
can exactly compute inner product and matrix factor-
ization, and thus it should be able to achieve accuracy
at least as good as approaches that do not use neural
networks. Because of the flexibility of this general-
ized approach, it has the potential to outperform direct
matrix factorization. For example, in a recommender
system, our approach facilitates augmenting user and
item profile vectors with static profile vectors for ad-
dressing the cold-start problem (Koren et al., 2009).
5 DISTANCE
Suppose we want to compute the distance between
A Continuum among Logarithmic, Linear, and Exponential Functions, and Its Potential to Improve Generalization in Neural Networks
483
p
3
Figure 5: A neural network implementation of squared dis-
tance using soft exponential as an activation function. To
compute Euclidean distance (the square root of this), only
one additional network unit would be required.
two vectors, p and q. This could also be done with a
neural network that uses soft exponential for its acti-
vation functions. To do this, we will use the property,
a
b
= e
blog
e
(a)
.
Figure 5 shows a neural network that computes the
squared distance between two vectors. (If you want
to take the square root, to make it Euclidean distance,
just change the unit in layer 3 to use α = −1, and add
a layer 4 with one unit. This unit would use α = 1,
and its incoming weight would be set to 0.5.)
6 RADIAL BASIS FUNCTION
NETWORKS
A gaussian radial basis kernel uses the formula,
e
−rs
,
where r is a weight that controls the squared radius
of the kernel, and s is either the squared distance be-
tween the input vector and the center of the kernel,
or the inner product with the input vector. This func-
tion is important to a number of classification mod-
els, including support vector machines that use a ra-
dial basis function and radial basis function networks
(Sch¨olkopf et al., 1997; Chen et al., 1991; Qasem and
Shamsuddin, 2011). This could be implemented in
a network using only f as an activation function by
simply adding a single unit with α = 1 to the neural
networks in Figures 4 or 5. The weight feeding into
this unit would be −r. If we added a layer to combine
several of these, we would have a radial basis function
network without using any specialized units.
Although it is already well-known that neural
networks are universal function approximators (Cy-
benko, 1989), it is worth noting that soft exponen-
tial enables common architectures to be exactly im-
plemented using a neural network with minimal ar-
chitectural overhead. If a simple model sufficiently
models a set of data, it is generally preferable and
yields better predictions than an unnecessarily com-
plex one. If these architectures were implemented us-
ing a network with a sigmoidal activation function,
for example, the resulting models would be very large
networks that would probably take more training data
to train it to generalize well.
7 FOURIER NETWORKS
Fourier neural networks use a sinusoidal activation
function to transform a signal from the time or space
domain to the frequency domain in a process similar
to the Fourier transform (Silvescu, 1999; Tan, 2006;
Zuo et al., 2009). If α is allowed to have a complex
value, soft exponential can be used as the activation
function in a Fourier neural network. Let α
r
be the
real component of α, and α
i
be the imaginary compo-
nent of α, such that α = α
r
+ iα
i
. For simplicity, we
assume that x is real, and α
r
= 0. Then the equation
for f becomes
f(α
i
, x) =
sin(α
i
x)
α
i
+ i
α
i
−
cos(α
i
x) + 1
α
i
. (8)
Without these assumptions, the resulting equation
contains several additional terms. Figures 6 and 7
show the real and imaginary components respectively
of f over a range of values for α
i
. It can be seen in
these figures that the imaginary component of α de-
termines the frequency of the sinusoidal wave. (Al-
though it also affects the amplitude, this is not signif-
icant because the outgoing weight can compensate to
achieve any desired amplitude).
We have shown that Fourier networks are effective
for extrapolating real-world time-series data (Gashler
and Ashmore, 2014). In a pending publication, we
showed that this approach is even more effective at
generalizing when it it combined with other activa-
tion functions (Godfrey and Gashler, 2015). Because
soft exponential can be logarithmic, exponential, lin-
ear, or sinusoidal when α is allowed to be complex,
we can create a Fourier network with only this activa-
tion function and achieve the same level of accuracy
for generalization and extrapolation.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
484

-15
-10
-5
0
5
10
15
-10
-5
0
5
10
x
f
(
α
)
,
x
r
i
Figure 6: A plot of the real component of soft exponential
over a range of values for α
i
.
8 PROPOSED ARCHITECTURE
We conclude our discussion by describing a deep neu-
ral network architecture that could potentially use this
novel activation function to autonomously achieve all
of these representational capabilities as needed to ad-
dress a wide range of challenges. Because complex
values for α cause each unit to output two values, in-
stead of one, it may not be immediately clear how to
apply such a network to arbitrary problems. How-
ever, if the α parameter values in the output layer are
constrained to take only real values, then this network
will behave like traditional neural networks, mapping
from any number of input values to any number of
output values. Allowing hidden units to take on com-
plex values for α should not present any problems be-
cause the additional values may simply be fed into the
next layer as if the preceding layer were twice as big.
Hence it should be reasonable to use f as the activa-
tion function for every unit in a deep neural network.
The α parameter for each unit could be initialized
to 0+ 0i. This has the very desirable property of ini-
tially causing the entire network to behave like lin-
ear regression. As training proceeds, it will take on
non-linearities only as necessary to fit the data. All of
the weights would be initialized with random values
drawn from a normal distribution, then normalized
such that the primary eigenvalue is 1. Since all of the
activation functions are initially the identity function,
the problem of vanishing gradients is initially miti-
gated, enabling very deep networks to be trained effi-
ciently. This activation function does not impose any
particular topology on the rest of the network, so the
layers could fully-connected or arranged with sparse
connections, such as in convolutional layers.
-15
-10
-5
0
5
10
15
-10
-5
0
5
10
x
x
f
(
α
)
,
i
i
Figure 7: A plot of the imaginary component of soft expo-
nential over a range of values for α
i
.
Likewise, the differentiability of soft exponential
facilitates optimization with batch gradient descent,
stochastic gradient descent, or many other optimiza-
tion techniques. α can be updated along with the
weights in the manner of steepest descent. L
1
regular-
ization should be applied to promote sparsity. It can
be observed that the various common architectures
that we can demonstrated with this activation function
use sparse connections. It follows, therefore, that L
1
regularization may be expected to work particularly
well with this activation function. Note that L
1
reg-
ularization can be applied to the α parameter as well
as the weights of the network. When α is pulled to-
ward zero, the network approaches linear regression.
Hence, regularizing the α parameter has the desirable
effect of causing the surface represented by the neural
network to straighten out.
9 CONCLUSION
We presented a novel activation function, soft expo-
nential, that continuously generalizes among logarith-
mic, linear, and exponential functions. This function
exhibits many desirable theoretical properties that
make it well-suited for use as an activation function
with neural networks. Empirical validation of these
theoretical properties still needs to be performed as
future work. Because of the significant potential that
this activation function has to impact the effective-
ness of deep neural networks, we are anxious to share
these ideas with the broader research community now,
instead of waiting for our attempts at achieving vali-
dation, so that the community may participate in the
process of discovering its potential and limitations.
A Continuum among Logarithmic, Linear, and Exponential Functions, and Its Potential to Improve Generalization in Neural Networks
485
REFERENCES
Berry, M. W., Brown, M., Langville, A. N., Pauca, V. P.,
and Plemmons, R. J. (2007). Algorithms and ap-
plications for approximate nonnegative matrix factor-
ization. Computational Statistics & Data Analysis,
52(1):155–173.
Brunet, J. P., Tamayo, P., Golub, T. R., and Mesirov, J. P.
(2004). Metagenes and molecular pattern discovery
using matrix factorization. Proceedings of the Na-
tional Academy of Sciences, 101(12):4164–4169.
Cai, J., Cand`es, E. J., and Shen, Z. (2010). A singular value
thresholding algorithm for matrix completion. SIAM
Journal on Optimization, 20(4):1956–1982.
Chen, S., Cowan, C. F., and Grant, P. M. (1991). Orthog-
onal least squares learning algorithm for radial basis
function networks. IEEE Transactions on Neural Net-
works, 2(2):302–309.
Cybenko, G. (1989). Approximation by superpositions of
a sigmoidal function. Mathematics of control, signals
and systems, 2(4):303–314.
Gashler, M. S. and Ashmore, S. C. (2014). Training deep
fourier neural networks to fit time-series data. Lecture
Notes in Bioinformatics, 8590:48–55.
Godfrey, L. B. and Gashler, M. S. (2015). Neural decompo-
sition of time-series data for effective generalization.
Publication Pending.
Kalman, B. L. and Kwasny, S. C. (1992). Why tanh: choos-
ing a sigmoidal function. In Neural Networks, 1992.
IJCNN., International Joint Conference on, volume 4,
pages 578–581. IEEE.
Koren, Y., Bell, R., and Volinsky, C. (2009). Matrix factor-
ization techniques for recommender systems. Com-
puter, 42(8):30–37.
Nair, V. and Hinton, G. E. (2010). Rectified linear units
improve restricted boltzmann machines. In Proceed-
ings of the 27th International Conference on Machine
Learning (ICML-10), pages 807–814.
Qasem, S. N. and Shamsuddin, S. M. (2011). Radial
basis function network based on time variant multi-
objective particle swarm optimization for medical dis-
eases diagnosis. Applied Soft Computing, 11(1):1427–
1438.
Sch¨olkopf, B., Sung, K.-K., Burges, C. J., Girosi, F.,
Niyogi, P., Poggio, T., and Vapnik, V. (1997). Com-
paring support vector machines with gaussian kernels
to radial basis function classifiers. Signal Processing,
IEEE Transactions on, 45(11):2758–2765.
Silvescu, A. (1999). Fourier neural networks. In Neural
Networks, 1999. IJCNN’99. International Joint Con-
ference on, volume 1, pages 488–491. IEEE.
Tan, H. (2006). Fourier neural networks and generalized
single hidden layer networks in aircraft engine fault
diagnostics. Journal of engineering for gas turbines
and power, 128(4):773–782.
Xu, W., Liu, X., and Gong, Y. (2003). Document clustering
based on non-negative matrix factorization. In Pro-
ceedings of the 26th annual international ACM SIGIR
conference on Research and development in informa-
tion retrieval, pages 267–273. ACM.
Zeiler, M. D., Ranzato, M., Monga, R., Mao, M., Yang,
K., Le, Q. V., Nguyen, P., Senior, A., Vanhoucke, V.,
Dean, J., et al. (2013). On rectified linear units for
speech processing. In Acoustics, Speech and Signal
Processing (ICASSP), 2013 IEEE International Con-
ference on, pages 3517–3521. IEEE.
Zuo, W., Zhu, Y., and Cai, L. (2009). Fourier-neural-
network-based learning control for a class of nonlinear
systems with flexible components. Neural Networks,
IEEE Transactions on, 20(1):139–151.
KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval
486
