The Vantage Point Bees Algorithm

Sultan Zeybek and Ebubekir Koç

Department of Computer Engineering, Fatih Sultan Mehmet Vakif University, Beyoglu, İstanbul, Turkey

Keywords: Bees Algorithm, Swarm Intelligence, Artificial Intelligence, Combinatorial Optimization, Local Search,

Vantage Point Trees, Nearest Neighbourhood Search.

Abstract: In this paper, an implementation of vantage point local search procedure for the Bees Algorithm (BA) in

combinatorial domains is presented. In its basic version, the BA employs a local search combined with

random search for both continuous and combinatorial domains. In this paper, a more robust local searching

strategy namely, vantage point procedure is exploited along with random search to deal with complex

combinatorial problems. This paper proposes a hybridization technique which involves the Bee Algorithm

(BA) and a local search technique based on Vantage Point Tree (VPTs) construction. Following a

description of the Vantage Point Bees Algorithm (VPBA), the paper presents the results obtained for several

local search strategies for BA, demonstrating efficiency and robustness of the VPBA.

1 INTRODUCTION

Many real-world engineering problems require the

searching of a system of variables in order to

optimize performance of a product and/or process.

They involve large number of finite solutions that

are encoded in real-valued variables or discrete

variables (Blum et al., 2003). A class of optimization

problems with discrete values called Combinatorial

Optimization Problems which can be defined as NP-

hard and many of them can not be solved exactly

within polynomially bounded computation times

(Pham et al., 2005).

Researchers have implemented different

strategies to deal with complex optimization

problems. Nature-inspired and population-based

metaheuristics often rely on stochastic search

methods based on swarm intelligence. They have

two major components namely: selection of the

fittest solutions and randomness (Yang, 2010).

The Bees Algorithm (BA) is one of the examples

of a nature inspired algorithm which mimics the

food foraging behaviour of honey bees. In its basic

version, the algorithm proposed a well-balanced

neighbourhood search combined with random

explorative search (Pham et al., 2005). The BA can

be used in order to solve optimization problems and

it is implemented for both continuous domains and

combinatorial domains. But research mainly focused

on continuous domains with many succesfull

applications and implementations (Pham, 2009).

There is major diffirence between these two domains

in terms of mathematical definition of distance (Koç,

2010). There are some studies present several

different local search strategies for the BA.

In this paper, an efficient and robust local search

algorithm with vantage point strategy is proposed to

increase the efficiency of the original algorithm for

combinatorial domains called the Vantage Point

Bees Algorithm (VPBA). Vantage point is a

selection procedure of a pivot element or vantage

point from metric space elements (combinatorial

search space elements) and the VPBA returns

pointer to the root of an optimized vantage point tree

algorithm with median calculations that satisfied the

local optimum value.

The paper gives brief description of bees in

nature, the BA and its local search strategy in

section 2. Section 3, gives the details of vantage

point approach in mathematical terms and presents

the VPBA with details and the advantages of using

Vantage Point Trees structures is explained. Problem

definition and experimental results presented in

section 3 and 4. The paper concluded with further

discussions in section 5.

340

Zeybek, S. and Koç, E..

The Vantage Point Bees Algorithm.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 340-345

ISBN: 978-989-758-157-1

2 THE BEES ALGORITHM

2.1 Bees in Nature and Foraging

Process

Honey bees have many different behaviours to

organise the complex structure of their colony in

nature. There are several examples of these

behaviours such as waggle dance. It is basically a

language that tells the bees direction and distance of

flower patches, along with their the quality ratings

(Frisch, 1967).

One of their most complex and efficient

behaviour is foraging for food. Scout bees search

randomly from one flower patch to another for

decent nectar sources when the foraging process

begins. After scout bees turns back to hive, they

perform the waggle dance on crowded parts of hive

(namely, the dance floor) to share the information

regarding directions, distances and quality ratings of

nectar sources.

2.2 The Bees Algorithm

The BA performs a kind of local search combined

with random. It has six parameters to set; number of

scout bees (n), number of selected sites (m), number

of top-ranking (elite) sites among the m selected

sites (e), number of bees recruited for each non-elite

site (nsp), number of bees recruited for each elite

site (nep), and neighbourhood size (ngh) and the

stopping criterion. The pseudo code of the BA is

shown in Figure 1, and the main algorithm

parameters are given in Table 1.

The algorithm starts with the n scout bees

randomly sample a solution space and, via fitness

function scout bees report the quality of visited

locations. This is the part of global search procedure

where scout bees explore the solution space

randomly and increase their chance to escape from

local optima.

Step 1: Initialise population with random solutions.

Step 2: Evaluate fitness of the population.

Step 3: While (stopping criterion not met) //Forming new

population.

Step 4: Select sites for neighbourhood search.

Step 5: Recruit bees for selected sites (more bees for best

e sites) and evaluate fitnesses.

Step 6: Select the fittest bee from each patch.

Step 7: Assign remaining bees to search randomly and

evaluate their fitnesses.

Step 8: End While.

Figure 1: Pseudo code of the basic bees algorithm (Pham

et al., 2005).

The algorithm then selects best bees with fittest

results from the solution space. Then it recruits

predefined number of bees around the selected sites

for local search. Again, fittest bees from each site

selected for further exploitation of the site (Pham et

al., 2005)

These steps are repeated until a stopping

criterion is met. At the end of each iteration,

population is updated and new population of the bee

colony is formed out representatives from each

selected patch and other scout bees assigned to

conduct random searches. New population generated

from neighbourhood search and global search phase

(Pham et al., 2005)

Table 1: Basic Parameters of the BA.

n number of scout bees

m number of selected sites

e number of elite sites out of m sites

nep recruited bees for elite sites

nsp number of bees recruited for the other

(m-e) selected sites

ngh neighbourhood size

3 THE VANTAGE POINT

NEIGHBOURHOOD SEARCH

FOR THE BEES ALGORITHM

3.1 Vantage Point Trees (VPTs)

In this section, details of the Vantage Point Tree

(VPTs) construction is presented. Searching in a

metric space includes several forms of vantage point

trees. (Yianilos, 1993). As a part of Nearest

Neihgbourhoud Search literature it is a data structure

and the algorithm that is used to search in metric

space with a distance function that satisfies the

triangle inequality (Chávez, 2001).

A metric space is defined as a pair of M =

(,d) where the set  denotes domain or search

space (universe) of valid objects (points, elements)

of the metric space sometimes called database,

dictionary or simply set of objects or elements. The

distance function

:    →  (1)

satisfies the following axioms:

i∀u





∈ d









 0positiveness,

ii∀u





∈ d









d









symmetry,

iii∀u ∈

d



u, u



 0reflexivity,

iv∀u







∈ d









d









d











triangleinequality,

The Vantage Point Bees Algorithm

341

then the pair (,d) is called a metric space. When the

elements of the metric space (,d) are n-tuples of

real numbers then the pair is called a finite-

dimensional vector space, if the elements are

identified with k real-valued coordinates (



,…,





the vector space is called k-dimensional vector

space. There are a number of options for the distance

function for instance the most commonly used is the

family of 



distances, defined as









,…,



 ,



,…,



 =

∑

|















/

(2)

As an example 



is the block or Manhattan

distance, 



is the well known Euclidean distance

and 



corresponds to taking the limit of the 



when s goes to infinity. The vantage point bees

algorithm with neighbourhood search procedure, we

used k = 2, we have a 2-dimensional search space

and the distance between two elements with standard

Euclidean metric.

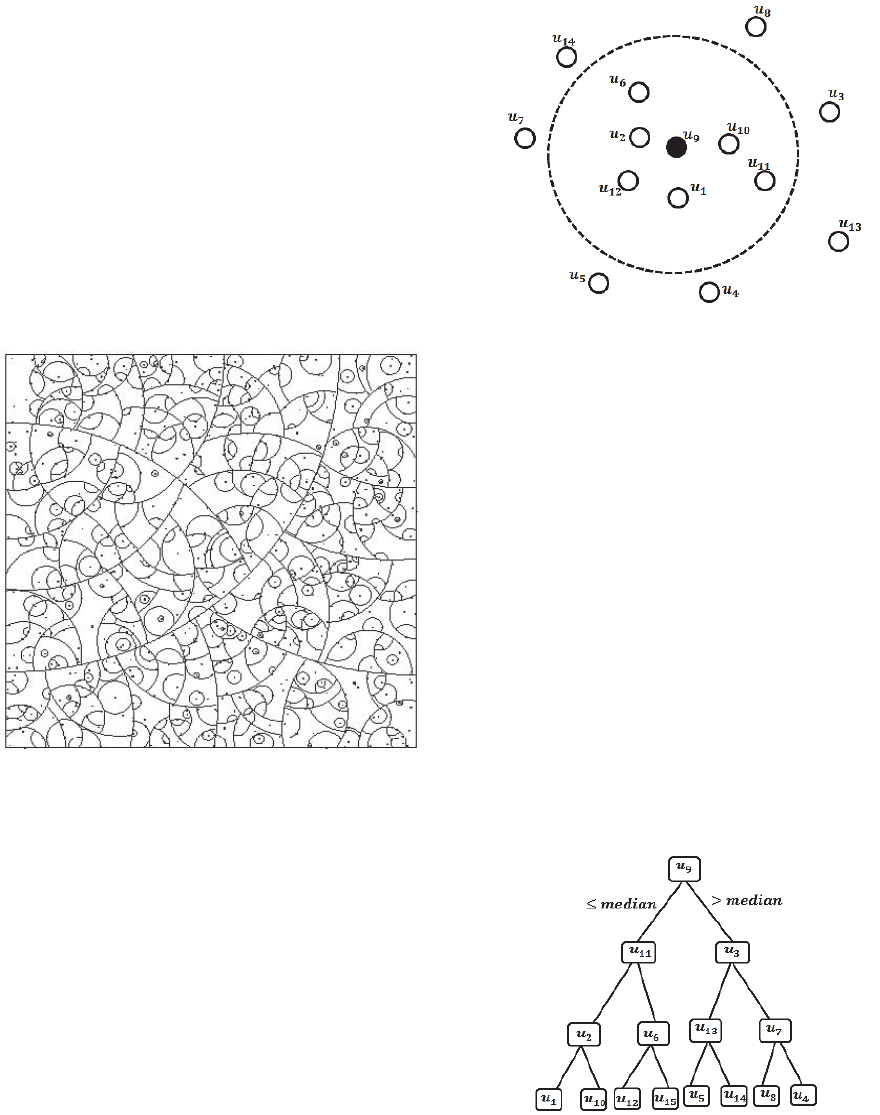
Figure 2: Vantage point decomposition (Yianilos, 1993).

The measure of distance between objects, for

example in the VPBA it denotes the measure of

distance between two sites. The distance function is

Euclidean metric. In this work, q is selected as a

pivot element sometimes called center or vantage

point that cuts/divide the entire space to form a

vantage point tree. Each element of metric space

distances to every other element formed a

perspective on the entire space.

The similarity-based queries commonly search

for all elements (points or sites) within some

spicified distance from a given query object and

require retrieval of the nearest neighbours of the

vantage point. For a given vantage point q, as the

selected site and vantage point tree basically

partitions the search space into spherical fields

around a chosen vantage point at each level which is

similar to first method in Burkhard and Keller

(1973) (Uhlmann, 1991).

Figure 3: Selecting vantage point 



and plot the radius M

used for the root 



(Chávez, 2001).

The median is found and the sites are partitoned into

two groups. The left side group containes the sites

whose distances to the vantage point are less then or

equal to median distance, the right side group

contains the sites whose distances are larger than the

madian distance.

Thus the structure of a binary vantage-point tree

is (q,m,



,



, where q is the vantage point, m is

the median distance among the distances of all the

sites (from q) indexed below that node, and 



is the

left branch of node,



is the right branch of node

(Bozkaya, 1999).

Vantage Point Trees (VPTs) formed by simplest

algorithm. Its distinguished vantage point then splits

the space into left and right space. This may be

defined as building a binary tree recursively, taking

any element p as the root (vantage point) and taking

the median of the set of all distances.

M = 



, 

∈



(3)

Figure 4: Example of VPTs with root 



(Chávez, 2001).

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

342

The left space or left subtree contains the elements

u, which satisfied ,   and right subtree

contains the elements u, which satisfied,   



. This subtrees with a selected vantage point

element is constructed by the algorithm randomly.

The VPTs takes O(n) space and is built in

O(nlogn) worst case time, since it is balanced.

(Chávez, 2001), the query complexity is argued to

be O(logn) (Yianilos, 1993) for small search radius.

3.2 The Vantage Point Bees Algorithm

The Vantage Point Bees Algorithm (VPBA)

proposed a hybridization technique which involves

the Bees Algorithm and a local search technique

based on Vantage Point Trees (VPTs).

Since the similarity criterion is a distance

function which satisfies the triangle inequality the

vantage point tree splits sites using absolute distance

from a single selected sites. The triangle inequality

which is used to find the upper and lower bounds of

the list of sites that are within our chosen distance

and only calculate the distance for those selected

sites, so it is reduced the number of distance

evaluations. Another advantages of VPTs structure

is that is although it is designed for the continuous

domains it can be used for discrete domains with

virtually no modifications (Chávez, 2001).Hence the

BA with VPTs local search procedure can be used

both for continuous and combinatorial domains

without a different approach of local search

strategies when it comes to a mathematical definiton

of the distance.

Step 1: Recurse the following steps until all sites are

chosen.

Step 2: Select a vantage point p

(pivot site) randomly

from the all sites.

Step 3: Add vantage point to the solution list; // i.e hist

list

Step 4: Calculate median of the set of all distances,

// return a list hist of the distances from the item to each

vantage point.

M =



, 

∈



Step 5: Splits site list into two list L and R. Take only left

site list (L) for optimal solution.

for (site=1; site  allSites; site ++)

if (,  

median) add site to L,

Step 6: Select new vantage point from the L randomly.

Add pivot site to the solution list and delete selected site

from all sites.

Step 7: Go to step 3, and repeat until convergence or

termination conditions are met.

Step 8: Return solution site list for evaluating fitness.

Figure 5: The Pseudo code of vantage point recruitment

phase.

The VPBA has the same six parameters, namely;

n, m, e, nsp, nep, ngh. Initially, a number of bees (n)

is sent randomly to the search space. Each bee is

associated with one solution. The solutions

representing the fitness of individual bees were then

ranked in descending order. The top m solutions

were regarded as selected sites. Out of m sites, a

number of top e site(s) is considered as elite one(s).

Each of non-elite (m-e) and elite (e) sites

respectively receives nsp and nep forager bees to

exploit the discovered food source.

The Pseudo code of vantage point recruitment

phase is given in Figure 5 and the pseudo code of the

VPBA is shown in Figure 6.

Step 1:Initial population with n random solution.

Step 2: Evaluate fitness of the population.

Step 3: While (stopping criterion not met)

Step 4: Select sites (m) for neighbourhood search.

Step 5: Recruit bees for selected sites, evaluate fitnesses,

select the fittest bee from each site.

for (k=l ; k=e ; k++)

// More bees for best e sites

for (Bee=l ; Bee= nep ; Bee++)

// Vantage Point Tree Recruitment Phase Start

BeesPositionlnNgh=GenerateVPTs(Bee(i),allsites)

// Evalute the fitnees of recruited Bee(i)

Evaluate Fitness = Bee(i);

If (Bee(i) is better then Bee(i-l))

RepresentativeBee = Bee(i);

// Other selected sites(m-e)

for (k=e ; k=m ; k++)

// Less Bees for Other Selected Sites (m-e)

for (Bee=l ; Bee= nsp ; Bee++)

BeesPositionlnNgh=GenerateVPTs(Bee(i),all sites),

// Evalute the fitnees of recruited Bee(i)

Evaluate Fitness = Bee(i);

Step 6: If (Bee(i) is better then Bee(i-l))

RepresentativeBee = Bee(i);

Step 7: Assign remaining bees to search randomly and

evaluate their fitnesses.

// (n-m) assigned to search randomly into whole solution

space.

Step 8: End While

Figure 6: Pseudo code of VPBA.

4 THE TRAVELLING SALESMAN

PROBLEM (TSP)

4.1 Symmetric Travelling Salesman

Problem

The Travelling Salesman Problem (TSP) can be

defined as finding a Hamiltonian path with

minimum cost. The salesman starts his tour from a

The Vantage Point Bees Algorithm

343

city and returns back to his starting city while

determining a minimum distance passing through

each city once and only once. It is a easy to describe

but difficult to solve problem, which is why it draws

so much attention from the scientific community.

This problem is a mathematical NP-hard problem

(Laporte, 1992) and it is important for many

different industries.

In this paper, the metric TSP deployed since

many other optimization models prefers to do so as a

standard. Let V is a set of m cities,   



,…,



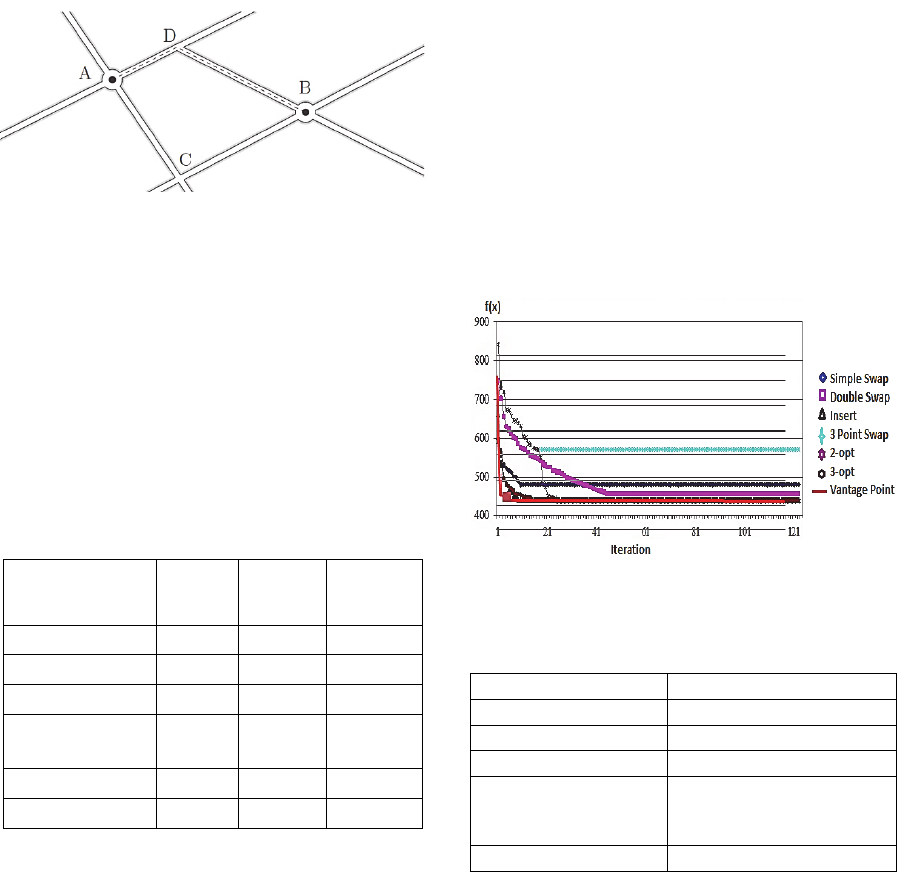
Metric TSP is satisfy the triangle inequality, see

Figure 7, and since the distance



,



) =



,





for every



,



∈, the problem is a symmetric TSP

and we find the optimal tour after each iteration of

VPTs recruitment phase.

Figure 7: Triangularity in a road network. The distance

from A to B is determined by the shortest route 



, 









, 







, 



for every X (Hetland, 2009).

4.2 Experimental Results

In this section, the performance of the VPBA is

evaluated. First, the efficiency of the algorithm is

presented in Table 2. The algorithm with new local

search strategy is run with several different data sets.

It proves that the VPBA is an efficient and robust

algorithm and it can converge local optima.

Table 2: Performance of VPBA for selected benchmark

problems in TSPLIB.

Problem

[Cities/evaluation]

VPBA

Best

Result

VPBA

Average

Iterations

Best

Known

Results

att48 [48/500] 10628 10823 10628

eil51[51/500] 426 436 426

eil76 [76/500] 538 565 538

kroa100[100/500] 22631

23511

21282

Eil101 [101/500] 668 681.96 629

d198 [198/500] 16752 17811 15780

Secondly the performance of the VPBA

compared with the BA results with several local

search strategies. The VPBA is significantly fast in

finding the optimal value of tested benchmark

function. The Vantage point local search procedure

improves the local search efficiency of the

algorithm.

The performance of the VPBA is investigated by

applying the algorithm to TSP taken from TSPLIB.

As an instance we choose Eil51, that is a 51-city

TSP problem and we compare the test result with the

performance of the BA with several local search

operators including simple (2 point) swap, double (4

point) swap, insert, 3 point swap, 2-Opt and 3-Opt.

The experiments were performed using the

VPBA to evolve its own parameter values. It was

run 100 times for each parameter setting on eil51

benchmark problem.

The computing platform used to perform the

experiments was a 2.50 GHz Intel(R) Core(TM) i5-

2450M CPU PC with 4 GB of RAM. The

experimental programs were coded in the Java

language and compiled with Eclipse IDE. Each

problem instance was run across 100 random seeds.

The parameters of Vantage Point Bees Algorithm for

Eil51 TSP shown in Table 3. Figure 8 summarizes

the results of the Bees Algorithm with (2 point)

swap, double (4 point) swap, insert, 3 point swap, 2-

Opt and 3-Opt operator on Eil51 TSP (Koç, 2010).

Figure 8: Benchmark results of the VPBA for a 51 city

TSP.

Table 3: The parameters of VPBA for experiments.

n = 80 number of scout bees

m = 40 number of selected sites

e = 5 number of elite sites

nep = 80 recruited bees for elite sites

nsp = 40

number of bees recruited

for the other

(m-e) selected sites

100 Number of iterations

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

344

The Eil51 problem was tested 100 independent

runs. From the experimental results the best tour

length and average tour length is selected. Standard

deviation of experiments is used to measure the

performance of benchmarked strategies. For each

data set the proposed algorithm can find the best tour

in almost each trial and the error rate is only 0.02%

away from the optimal. Standard deviation over 100

runs is 1,08358.

5 CONCLUSIONS

An improved version of the BA is presented with a

new local search strategy which is called the

Vantage Point Bees Algorithm (VPBA). The

performance of the VPBA was significantly fast in

finding the optimal optimum of tested benchmark

function.

The performance of the VPBA was evaluated

using 51-city TSP and the results were compared

with The Bees Algorithm with several local search

operators including simple (2 point) swap, double (4

point) swap, insert, 3 point swap, 2-Opt and 3-Opt.

Results shows that the VPBA outperformed the BA

with several other local search strategies.

REFERENCES

Bonabeau, E., Dorigo, M., and Theraulaz, G. 1999. Swarm

intelligence: From Natural to Artificial Systems.

Oxford University Press, Oxford.

Blum, C., Roli, A., 2003. Metaheuristics in combinatorial

optimization: Overview and conceptual comparison.

ACM Computing Surveys. pp. 268–308.

Bozkaya, T., Ozsoylu, M., 1999. Indexing Large Metric

Spaces for Similarity Search Queries. ACM

Transactions on Database Systems (TODS).

Burkhard, W., Keller, R., 1973. Some approaches to best-

matching file searching. Comm. of the ACM.

Chávez, E., Navarro, G., Baeza-Yates, R., and Marroquín,

J., L., 2001. Searching in metric spaces. ACM

computing surveys (CSUR).

Frisch, K., 1967. The Dance Language and Orientation of

Bees. Cambridge, Mass, The Belknap Press of Harvard

University Press.

Hetland, M., L.,2009. The Basic Principles of Metric

Indexing.

Johnson, D., S., and McGeoch, L., A., 1997. The traveling

salesman problem: A case study in local optimization.

Laporte, G., 1992. The traveling salesman problem: An

overview of exact and approximate algorithms.

European Journal of Operational Research, vol. 59, no.

2, pp. 231-247.

Pham, D., T., Ghanbarzadeh A., Koç, E., Otri, S., Rahim,

S. and Zaidi, M., 2005. The Bees Algorithm. Technical

Note, Manufacturing Engineering Centre, Cardiff

University, UK.

Pham, D., T., Ghanbarzadeh, A., Koç, E., Otri, S., Rahim,

S. and Zaidi, M. 2006. The Bees Algorithm - A Novel

Tool for Complex Optimisation Problems. In

Proceedings of the Second International Virtual

Conference on Intelligent production machines and

systems, Elsevier, Oxford, 2006, pp. 454–459.

Pham, D., T., Castellani, M., 2009. The bees algorithm:

Modelling foraging behaviour to solve continuous

optimization problems. Proceedings of the Institution

of Mechanical Engineers, Part C: Journal of

Mechanical Engineering Science 223(12), pp. 2919-

2938.

Kelly, J., K., 1955. General Topology. New York: D. Van

Nostrand.

Kennedy, J., Eberhart, R., Shi, Y., 2001. Swarm

Intelligence. Academic Press, London.

Koç, E., 2010. The Bees Algorithm Theory , Improvements

and Applications, PhD. Manufacturing Engineering

Centre School of Engineering University of Wales,

Cardiff, United Kingdom.

Liu, Y. and Passino, K., M., 2000. Swarm Intelligence:

Literature Overview. Dept. of Electrical Engineering,

The Ohio State University.

Seeley, T., D., 1996. The wisdom of the hive: The social

physiology of honey bee colonies. Cambridge,

Massachusetts: Harvard University Press.

Uhlmann, J., K., 1991. Satisfying General

Proximity/Similarity Queries with Metric Trees.

Information Processing Letters.

Uhlmann, J., K., 1991. Metric Trees. Applied Mathematics

Letters, vol. 4, no. 5.

Yang, X., S., 2008. Nature-inspired Metaheuristic

Algorithm. Bristol UK: Luniver Press.

Yang, X., S., 2010. Engineering Optimization: An

Introduction with Metaheuristic Applications. Wiley,

Chichester.

Yianilos, P., N., 1993. Data structures and algorithms for

nearest neighbor search in general metric spaces. In

Proceedings of the fourth annual ACM-SIAM

Symposium on Discrete algorithms, PA, USA, Society

for Industrial and Applied Mathematics.

The Vantage Point Bees Algorithm

345