L2 Designer

Language and Tool for Generative Art

Tomáš Konrády, Barbora Tesařová and Kamila Štekerová

Faculty of Informatics and Management, University of Hradec Králové, Hradec Králové, Czech Republic

Keywords: Formal Grammar, Generative Art, Genetic Programming, L-System.

Abstract: We propose a new formal grammar (L2 language) and its implementation in JavaScript tool (L2 Designer).

The L2 language allows us to create formal definition of the hierarchy of L-systems encapsulated in L-

scripts. The L2 Designer enables creation of initial L-system, its modifications based on genetic

programming and iterative evolution, and graphical interpretation. We provide an example of L2 program

and we illustrate possibilities of L2 Designer on a case study which was inspired by an artistic decorative

floral pattern.

1 INTRODUCTION

Lindenmayer systems (L-systems) are formal

grammars with parallel rewriting mechanism that

were originally developed for modelling and

visualization of the growth process of various types

of algae (Lindenmayer, 1968). Later they were

applied in the field of computer graphics. The best

known graphical interpretation of L-systems is based

on usage of a relative cursor upon a Cartesian plane

(turtle graphics). The L-systems are frequently used

in combination with evolutionary techniques, e.g.

(Hornby, 2001) presents a parametric L-system for

drawing virtual creatures for computer animations.

In this contribution we explore the emergence

phenomena growing from combination of L-

systems, genetic programming and interactive

evolution, especially we are interested in its

application in generative art and artificial creativity.

We were inspired by shape grammars that also

originate from the theory of formal grammars: it was

shown that even simple rules of shape grammars

produce complex results (Stiny, 1994), moreover

(Chakrabarti et. al., 2011) applied shape grammars

in design.

The key issue in our research area is the

definition of the fitness function. Artificial neural

networks or design principles measurements are

well-applicable techniques (Galanter, 2012), for

relevant results see e.g. (Ashlock and Bryden, 2004),

(McCormack, 2003), (McCormack, 2008) or

(Bergen and Ross 2013).

The graphical interpretation of L-system:

strongly depends on its definition, because even

minor changes of parameters lead to completely

different and surprising results. Here the

evolutionary techniques help to search the large

space of parameters and to modify production rules.

Current implementations of the L-system

theory are based on extensions of general purpose

programming languages. From the technical point of

view, languages such as L+C (Karwowski and

Prusinkiewicz 2003), L-Py (Boudon et al. 2012) or

XL (Kniemeyer and Kurth, 2008) are complex and

their implementations are platform dependent. Our

intention is to provide easy-to-use tool for partly

interactive creation of various types of graphical

outputs. On the contrary, our tool does not make

user to directly write production rules, in fact the

user does not need to know the grammar of the L-

system at all.

In following sections of this paper we propose a

new formal language (L2 language) which is easy to

parse to the tree representation. Then we provide a

plaftorm independent tool (L2 Designer) which

enables specification of L-systems within L2

language, with its subsequent evolution based on

genetic programming. Finally, the graphical

interpretation of outputs is presented.

352

Konrády, T., Tesa

rová, B. and Štekerová, K..

L2 Designer - Language and Tool for Generative Art.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 352-357

ISBN: 978-989-758-157-1

2 L2 LANGUAGE

L2 language is designed for defining stochastic

context free parametric L-systems grammars. In

contrast to L+C or L-py, L2 does not include

anything else but features that we need for the

purpose of the definition of L-system. As well as

L+C, L2 supports the advanced properties of L-

systems:

 Sub-L-systems – it is possible to divide

large L-systems into smaller reusable parts,



Interpretation production rules – it lets us

separate topology of the L-system from its

representation, therefore the application of

genetic programming operators is easier.

For detail specification of L2 language, see (L2

Documentation, 2015). Here we provide a sample

code. Its explanation and interpretation is shown

below.

Example 1: L2 sample code.

alphabet Turtle2D {

F, f, L, R, PU, PS

};

$black = __rgb(0,0,0,255);

lscript BranchingLScript {

lsystem Bloom(F(0.01), 3)

using Turtle2D {

$angle = 90;

$colorA = __rgb(255,100,0,200);

$colorB = __rgb(150,50,50,200);

F(a) -->

F($a) L($angle) F($a) A($a);

F(a) -->

F($a) R($angle) F($a) A($a);

F(a) -h>

F($a, 0.003, __rgb(0,0,0,0));

A(a) -h>

[ F(0.0001, $a * 1.5 *

__random(), $colorA) ] |

[ F(0.0001, $a * 1.5 *

__random(), $colorB) ];

};

lsystem Branching(G(0.1), 4)

using Turtle2D {

$ratio = 0.9;

$angle = 60;

$anglePrec = 50;

$stroke = 0.003;

G(a) -->

F($a) [ L($angle)

G($ratio * $a)B($a) ]

[ R($angle) G($ratio * $a)

B($a) ];

L(a) -h>

L($a - $anglePrec * 0.5);

R(a) -h>

($a

anglePrec * 0.5);

F(a) -h>

F($a, $stroke, $black)

[

sublsystem Bloom(F($a / 10),

6)];

};

main call Branching();

};

derive BranchingLScript;

As shown in Example 1, the L2 program consists of

three main parts:

 Alphabet - a set of symbols (line 1),

 L-script encapsulating L-systems (line 5),

 L-system - the unit defining production rules,

default axiom and default number of derivations

(lines 6, 23).

The user can add variables (line 4). Variable names

start with symbol

$. The L-script contains the main

L-system (line 43). Start of the derivation of the L-

script is done by derive statement (line 45) resulting

in string of the modules.

BranchingLScript contains a definition of two L-

systems called Branching and Bloom (lines 6–22,

23–42). The heading of the L-system consists of:

 name,

 default axiom,

 default number of derivations,

 alphabet.

The body of L-systems includes the list of

productions. For the L-system productions we use

either the --> operator (line 11) or the –h> for

interpretation rules (line 15). The replacement string

on the right side of the production rule can contain

sublsystem statement (line 40) that calls derivation

of the other L-system within the same L-script.

3 L2JS LIBRARY

The L2 language is accessible within our L2JS

library which is the core of L2 Designer. The library

includes compiler, interpreter and module for

genetic programming.

The compiler of the L2JS library translates L2 to

JavaScript (Figure 1). The scripting language was

chosen due to its flexibility, dynamic scoping,

closures and both functional and object-oriented

programming support.

L2 Designer - Language and Tool for Generative Art

353

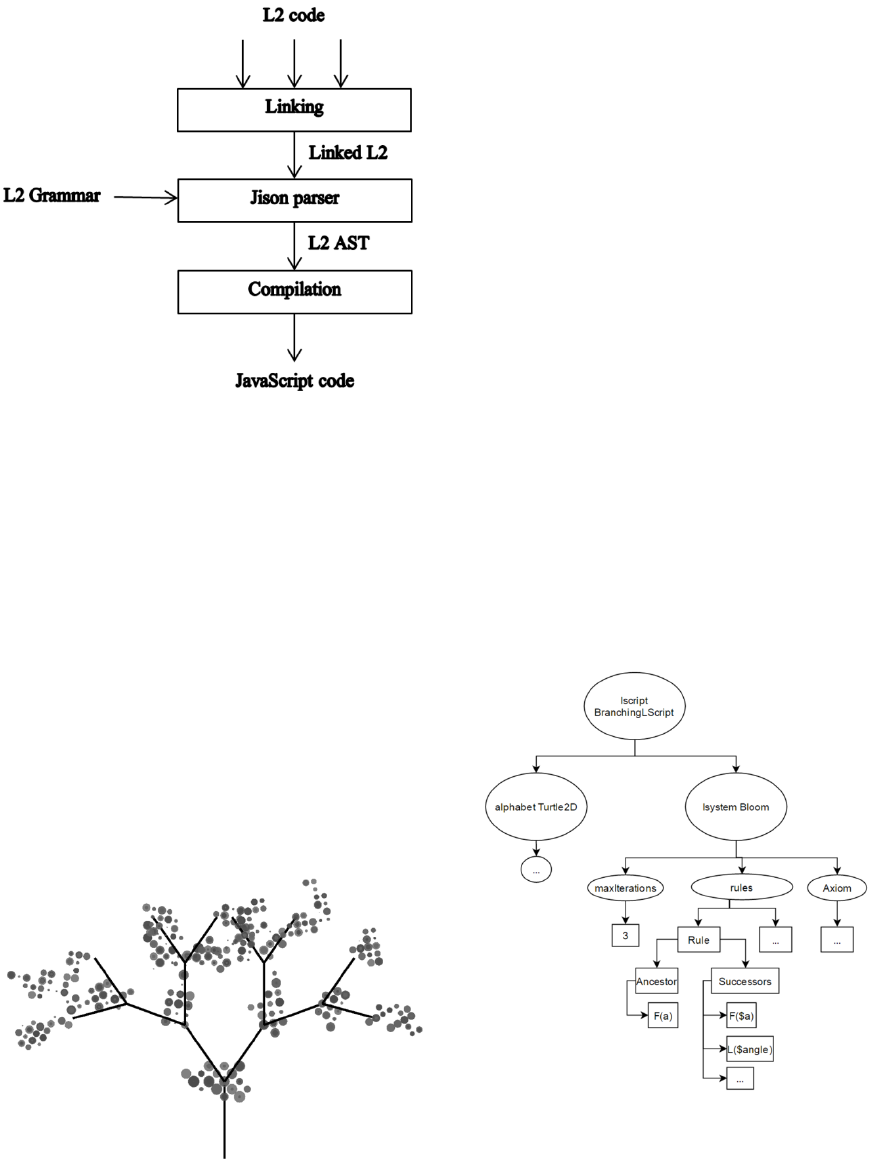
Figure 1: Scheme of the L2JS library.

The usage of JavaScript allows us to distribute the

computing within the web browser and Node.js web

server. The compilation starts with the linking of the

input source files. The whole code is parsed by Jison

parser into the abstract syntax tree (AST). The AST

consists of the nodes representing statements,

arguments, entities, names, variables and

expressions. Jison is a JavaScript implementation of

the combination of (Flex, 2015) and (Bison, 2015).

The parser requires the L2 grammar description file.

After the L2 AST is created by Jison, the translation

to the JavaScript code can be performed.

Our compiler is able to decompile L2 AST back

to the L2 code. This feature is essential for further

application of genetic programming.

The output of the compilation process is a

JavaScript program representing the derivation of

the L-script.

Figure 2: Turtle graphics for the sample code.

The Interpreter operates with an alphabet of the

L-system to resolve the type of interpretation. In our

sample code, an alphabet Turtle2D is used. Symbols

of the alphabet are understood as the instructions for

the turtle graphics (Figure 2).

The Interpreter works with rules that specify how

symbols are related to the set of statements from the

alphabet. E.g. the module F(a) is replaced with

$a, 0.003, __rgb(0,0,0,0)) according to

the corresponding interpretation rule (lines 15–16).

The interpretation in this particular case results in a-

long line with 0.003 size filled with transparent

colour.

The Evolver implements the L-system genetic

programming over the hierarchy of L-systems in L2

language. Details are provided in the next section.

4 GENETIC PROGRAMMING

Genetic programming is involved in the process of

iterative modifications of L-scripts.

After the initial L-script is provided to the

Evolver module, it becomes the base for the initial

generation. Each individual is represented by the L-

script which is converted to L2 AST (see Figure 3

for illustration). The user has to specify which of

sub-L-systems should be modified by the Evolver.

Figure 3: Example of simple AST of L2 script.

The genotype for the Evolver is represented by a tree

data structure, as it was originally introduced by

(Koza, 2000). Genetic operators modify the abstract

syntax trees using crossover or mutation. The

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

354

genetic operators designed for the parametric L-

systems were originally proposed by (McCormack,

2008).

In our case each part of AST has to its special

operators. The operators are applied either on the L-

systems (axiom, production rules) or on the

expressions used within the program (variable

assignments, expressions within modules). The

Evolver module supports:

 mutation of production rules,

 crossover of production rules,

 mutation of expressions – variation,

creation and colour mutation.

The main task was to identify the right terminals.

We found the way of an automatic detection of

terminals without the need of its explicit

specification by the user.

In case of production rule mutation, the set of

terminals consists of distinct symbols occurring in

all production rules of parent L-system. In case of

expression mutation the set of terminals depends on

the context of expression. On the other hand the

terminals within the rule are enriched with

parameters from the ancestor of the rule.

The Evolver implements two types of mutations.

The first of them modifies the numbers only

(variation mutation), the second one generates new

expressions (creative mutation).

Special mutation operator was developed for the

colours: user can specify maximum percentage of

modification for each of the channel of the colour

model. For hue channel it is possible to specify an

exact angle that can be added or reduced.

We represent production rules using target tree

structures similarly to (Jacob, 1994). Every leaf is a

module of the rule and every new level of the tree is

determined by stack symbols ([, ]).

The crossover is represented by an exchange of

the branches from the tree representation of L-

systems. The newly created production rule either

replaces the rule which was selected for the

crossover (parent rule) or is added to the definition

of the L-system. Probability of the newly created

rule is determined by product of the probability of

parent rule and a predefined constant.

In the process of the fitness evaluation, the user

selects the best solutions generated by the program

and assigns the integer fitness values to these

solutions. This approach is known as interactive

evolutionary computation (IEC). In comparison with

other methods, IEC is more time consuming, only

small populations and low number of generations

can be processed effectively. On the other hand,

with IEC the user can apply his aesthetic

preferences.

The rank selection mechanism is combined with

elitism. For details of this method see (Sivaraj and

Ravichandran, 2011).

5 IMPLEMENTATION

The L2 Designer is a web-based JavaScript

application enabling the interactive designing of L-

systems. The core of the application is L2JS library.

The server is running on Node.js. Other main

technologies we are using are MongoDB and

Angular.js.

Figure 4: Interface of L2 Designer with a visualization of

L-system.

Within the L2 Designer the user can manage

projects and directories of scripts. The main focus is

on the process of designing new L-systems (Figure

4). The source codes are available together with their

interpretations.

6 CASE STUDY

Let us demonstrate the L2 Designer workflow. The

decorative floral pattern Michaelmas Daisy 1929

(The Warner Textile Archive, 2015) was our

inspiration.

The process starts with creation of L-script

which contains several sub-L-systems. The first part

of L-systems represents basic shapes (flower petal,

leaf, disc floret); the second part represents a layout

of basic shapes (flower head, layout of flowers,

layout of leaves).

The aim of interactive evolutionary computation

(IEC) is to increase the similarity of the output

graphic interpretation of L-system with the original

pattern. The original pattern background is covered

with leaves. The interpretation of the L-system

before and after the process of IEC is shown on

Figures 5 and 6.

L2 Designer - Language and Tool for Generative Art

355

Figure 5: Layout of leaves before the interactive evolution

computation: completely regular distribution of leaves of

one size, with limited number of colour shades.

Figure 6: Layout of leaves after the interactive evolution

computation: irregular distribution of leaves on the canvas,

higher number of colour shades and variable sizes.

The next step is the creation of the main L-system

which generates the layout of flowers. Firstly it is

necessary to define L-system for random distribution

of flower heads over the canvas. This initial result

still does not correspond to the original artefact

(Figure 7): there is a lack of the grouping of flowers

of the same type. Again, this issue can be solved by

evolution of the L-system.

See Figure 8 for the final pattern. Notice that our L-

script does not cope in any way with external image

files or predefined patterns. Every shape is produced

solely by the turtle graphics interpretation of our L2

script. The source code of the L-script is available

online (L-script Examples, 2015).

For more graphical outputs produced by L2

Designer see (Konrády, 2014).

Figure 7: Random distribution of flowers.

Figure 8: Final pattern resulting from the evolution of L-

system.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

356

7 CONCLUSIONS

The current version of L2 Designer is capable of

evolving stochastic parametric L-systems which are

described by L2 language and generate complex

graphical patterns.

Our next intention is to improve the

effectiveness of genetic operators to speed up the

fitness evaluation. For that we are going to

implement a module for the processing of user’s

input using graphic tablet or vector image file.

The development of L2 language continues. New

features will be added such as decomposition rules

or rule conditions.

Finally, with respect to the generative art

applications, we want to explore the possibility of

integration of L2 Designer with graphical editors to

support creativity in users.

ACKNOWLEDGEMENTS

This work was supported by the University of

Hradec Králové under the specific research project

7/2015.

REFERENCES

Ashlock, D., Bryden, K.M., 2004. Evolutionary control of

Lsystem interpretation. CEC2004, vol. 2, pp.2273–

2279.

Bergen, S., Ross, B.J., 2013. Aesthetic 3D model

evolution. Genet. Program. Evol. Mach. 14, pp.339–

367.

Bison, 2015. http://www.gnu.org/software/bison/

Boudon, F. et al., 2012. L-Py: an L-system simulation

framework for modeling plant architecture

development based on a dynamic language. Front.

Plant Sci. 3(76).

Flex, 2015. http://flex.sourceforge.net/

Galanter, P., 2012. Computational Aesthetic Evaluation:

Past and Future. In: McCormack, J., d’ Inverno, M.

(Eds.): Computers and Creativity. Springer, pp.255–

293.

Chakrabarti, A., Shea, K., Stone, R. et al. , 2011.

Computer-Based Design Synthesis Research: An

Overview. J. Comput. Inf. Sci. Eng 11, 021003–

021003.

JacoHornby, G.S., Pollack, J.B., 2001. Evolving L-

systems to generate virtual creatures. Computers &

Graphics, Artificial Life 25, pp. 1041–1048.

doi:10.1016/S0097-8493(01)00157-1.

Jacob, C., 1994. Genetic L-system programming, in:

Parallel Problem Solving from Nature—PPSN III.

Springer, pp.333–343.

Jison, 2015. http://zaach.github.io/jison/

Karwowski, R., Prusinkiewicz, P., 2003. Design and

Implementation of the L+C Modeling Language,

Electronic Notes in Theoretical Computer Science,

86(2), pp.134-152.

Kniemeyer, O., Kurth, W., 2008. The Modelling Platform

GroIMP and the Programming Language XL, in:

Schürr, A., Nagl, M., Zündorf, A. (Eds.), Applications

of Graph Transformations with Industrial Relevance,

LNCS, Springer pp.570–572.

Konrády, T. 2015. L2 documentation.

https://github.com/tommmyy/l2js.

Koza, J.R., 2000. Genetic programming. 1: On the

programming of computers by means of natural

selection, MIT Press.

L2 documentation, 2015.

https://github.com/tommmyy/l2js.

Lindenmayer, A., 1968. Mathematical models for cellular

interactions in development. J. of Theoretical Biology,

Elsevier, Part I and II, pp.280–315.

L-script Examples, 2015.

https://github.com/tommmyy/l2js.

McCormack, J., 2003, The Application of L-systems and

Developmental Models to Computer Art, Animation

and Music Synthesis.

http://www.csse.monash.edu.au/~jonmc/research/thesi

s.html.

McCormack, J., 2008. Evolutionary L-systems, in:

Hingston, P.F., Barone, L.C., Michalewicz, Z. (Eds.),

Design by Evolution, Natural Computing Series.

Springer Berlin Heidelberg, pp.169–196.

Node.js, 2015 https://nodejs.org/

Sivaraj, R., Ravichandran, T., 2011. A Review of

Selection Methods in Genetic Algorithm. International

Journal of Engineering Science & Technology 3.

Stiny, G., 1994. Shape rules: closure, continuity, and

emergence. Environment and Planning B: Planning

and Design 21, pp.49 – 78.

The Warner Textile Archive, 2015.

http://www.warnertextilearchive.co.uk/

L2 Designer - Language and Tool for Generative Art

357