The Ground Reaction Force of Standing Triple Long Jump

Chung-Yu Chen, Chung-Ming Chan, Chien-Kuo Wu, Ya-Ling Chi and Chi-Wen Chang

Graduate School of Physical Education, National Taiwan University of Sport, Taichung, Taiwan

Keywords: Standing Long Jump, Ground Reaction Force, Kinetics.

Abstract: The purpose of this study was to investigate the characteristics of ground reaction force (GRF) for standing

triple long jump with the quantitative analysis of force platform in biomechanics, and also to compare the

differences of GRF and impulse among jump movements and standing long jump. Thirteen high school

athletes participated for this study. Six Kistler force platforms (9260AA6, 1000 Hz) were used to record the

GRF data during the participant performed the movements of standing long jump and standing triple long

jump. The results showed that the every jump distance of standing triple long jump was only the 0.92-0.95

times as the maximal standing long jump. The performance of the 3rd jump was less consistent, because of

the continuous jump movement of task constraint and the larger impact force (4.49 ± 1.53 BW) during

landing.

1 OBJECTIVES

During walking or jogging, the person will perform

the movements in the appropriate or optimal stride

length to adapt the requirements of task or/and

environment. The characteristic of maximum

movement following a maximum movement is an

issue of this study. The movement pattern of

walking or running shows that the main extensors of

lower extremity will be lengthened to decrease the

downward trend during the initial stage of landing,

and the main extensors will shorten immediately to

accelerate the body upward to takeoff.

The standing triple long jump is one of event of

entrance examination of sport related department in

Taiwan. Unlike the submaximal movement of

supporting training, such as double-leg hop

progression, alternate leg bound, etc., the standing

triple long jump is asked to reach the maximal

displacement in two continuous horizontal jumps

following standing long jump. But will the

continuous long jumps following utmost standing

long jump be affected by the larger impact force or

the instable movement? The purpose of this study is

therefore to investigate the characteristics of ground

reaction force (GRF) for standing triple long jump

through the quantitative analysis of force platform,

and to compare the differences of GRF and impulse

among jump movements and standing long jump.

2 METHODS

Thirteen male high school athletes (17.3 ± 0.7 years,

1.71 ± 0.06 cm, 67.7 ± 11.5 kg, mean ± SD)

participated in this study. They were training

regularly without history of lower extremity injuries.

The testing procedures were explained to each

participant. All participants signed an informed

consent form approved by the Ethical Advisory

Committee of Tsaotun Psychiatric Center, Ministry

of Health and Welfare of Taiwan (IRB No: 104022)

before the start of testing.

Participants were instructed to perform standing

long jump and standing triple long jump. Two

successful trials were recorded at each movement.

GRFs were acquired at 1000 Hz using six Kistler

force platfroms (9260AA6) with 64 channels data

acquisition system (5695B) for every jump. The

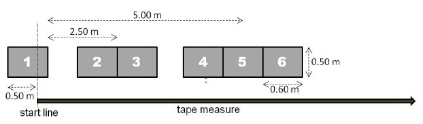
detail of the set-up of force platforms are shown as

figure 1.

Figure 1: Schematic drawings of the set-up of six force

platforms.

Chen, C., Chan, C., Wu, C., Chi, Y. and Chang, C..

The Ground Reaction Force of Standing Triple Long Jump.

Table 1: Means, standard deviation, and analysis of variance (ANOVA) results for effects of standing triple long jump and

standing long jump (SLJ) on kinematical and GRF variables.

Variable 1st 2nd 3rd SLJ F(3, 36)

Tukey’s test

Distance (m) 2.61

(0.22)

2.62

(0.29)

2.71

(0.28)

2.85

(0.30)

3.26* .214

SLJ > 1st, 2nd

Takeoff V

(m/s) 3.28

(0.13)

3.54

(0.31)

3.81

(0.20)

3.36

(0.17)

23.52* .662

3rd > 2nd > 1st, SLJ

Takeoff V

(m/s) 1.75

(0.19)

2.18

(0.27)

2.04

(0.32)

1.83

(0.28)

10.25* .461

2nd > 1st, SLJ;

3rd > 1st

Angle of takeoff (deg) 28.08

(3.08)

31.68

(3.76)

28.01

(3.84)

28.53

(3.62)

5.08* .298

2nd > 1st, 3rd, SLJ

Peak active GRF

(N) 778.7

(140.3)

611.6

(130.5)

615.9

(91.7)

789.3

(146.7)

48.46* .802

1st, SLJ > 2nd, 3rd

Peak active GRF

(N) 1431.7

(301.2)

2159.3

(391.2)

2137.7

(556.1)

1427.5

(311.5)

49.41* .805

2nd, 3rd > 1st, SLJ

*p < .05. Note: x - horizontal, y – vertical

The first and the second landing positions of

standing triple long jump were estimated by the

center of pressure of force platforms. The total

distance of standing triple long jump was decided by

the center of pressure of force platform 1 plus the

distance from tape measure. The distance of

standing long jump was quantified from the distance

of the center of pressure of force platform 1 and the

center of pressure of force platform 2-3. The vertical

and horizontal center of mass velocities were

estimated using the impulse method.

Repeated measures one way ANOVA with

Tukey’s post-hoc test were applied to examine the

differences in the kinetics and kinematics data

between jumps and landings (α = .05).

3 RESULTS

The analysis of reliability across trials showed the

distances of the first jump, the second jump, the

third jump, and the standing long jump were ICC

= .766, .628, .373, and .876, respectively. The ICCs

across trials of peak active vertical GRFs for each

jump were .889-.991, but the ICCs of peak active

horizontal GRFs for the first jump, the second jump,

the third jump, and the standing long jump

were .970, .884, .726, and .991, respectively.

There were significant differences in the jump

distances, F(3, 36) = 3.26, p = .032, η

= .214. The

Tukey’s post-hoc test showed the SLJ was longer

than the first and second jump of standing triple long

jump (table 1). The results of takeoff velocity

showed that the angle of takeoff at the second jump

was the greatest, F(3, 36) = 5.08, p = .005, η

= .298.

The statistical results of biomechanical parameters

are showed as Table 1.

4 DISCUSSION

The analysis of reliability showed the distances of

two jump trials of SLJ and the first jump of standing

triple long jump were consistency highly. But the

jump distance of consistencies were reduced during

the second and the third jumps of standing triple

long jump. It indicated that the standing triple long

jump is asked the utmost jumping movement

following two feet landing. The performer had to

adapt the landing impact following the process of

quite long flight, and it increased the variability of

movement to perform the takeoff movement

continually.

The distance of each jump of standing triple long

jump was 92-95% of the maximal SLJ. Although the

statistical analysis showed that the first and second

jumps were less than SLJ, and the distances of three

jumps were no differences. These indicated that the

most performers did not jump longer than the

maximal SLJ during every jump of standing triple

long jump. The initial impact peak in vertical GRFs

were 3.47 BW and 4.49 BW at the second (the first

landing) and third (the second landing) jumps,

respectively. Such higher load of impact force could

inhibit the mechanism of pre-stretch for leg

extensors; as a result, it explained the cause that the

consistency was decreased during the second and

third jump of standing triple long jump.

In conclusion, the results showed that the every

jump distance of standing triple long jump was only

the 0.92-0.95 times as the maximal standing long

jump. The performance of the third jump was less

consistent, because the continuous jump movement

of task constraint and the larger impact force during

landing.

REFERENCES

Birkimer, J., & Brown, J., (1979) Back to Basic:

Percentage agreement measures are adequate but are

easier ways Journal of applied behaviour analysis (12)

535-543

Cronbach, L. (1951) Coefficient alpha and the internal

structure of tests Psychometrika, (16) 297–334

Dudley, L., Smith, C., Olson, B., Chimera, N., Schmitz, B.,

and Warren, M. (2013) Interrater and Intrarater

Reliability of the Tuck Jump Assessment by Health

Professionals of Varied Educational Backgrounds

Journal of Sports Medicine, (2013) 1-5

Herrington, L., Myer, G., Munro, A. (2013) Intra and

inter-tester reliability of the tuck jump assessment

Physical Therapy in Sport, (14) 152-155

Kotter, J., Audige, L., Brorson, S., Donner, A., Gajewski,

B., Hrobjartsson, A., Roberts, C., Shoukri, M.,

Streiner, D. (2011) Guidelines for Reporting

Reliability and Agreement Studies (GRRAS) were

proposed Journal of Clinical Epidemiology, (64) 96-

106

Myer, G., Ford, K., and Hewett, T., (2008) Tuck jump

assessment for reducing anterior cruciate ligament

injury risk, Athletic Therapy Today, (13) 39-44